网络Meta分析研究进展系列（五）：诊断试验准确性网络Meta分析

高亚，孙凤，武珊珊，杨智荣，董圣杰，张天嵩，田金徽

随着越来越多的卫生技术人员在实施新的诊断措施之前查阅证据，诊断性试验系统评价/Meta分析在医疗保健中也将发挥越来越重要的作用[1-3]。但目前发表的诊断性试验Meta分析多评估单个诊断性试验的诊断价值，而在临床实践中和决策制定时，经常需要同时评估具有多个诊断阈值的多个诊断性试验的准确性，以找出哪个诊断性试验在哪个阈值上最有效或有最佳的成本效益[4]，这时传统的诊断性试验Meta分析便不适用。在干预性研究中，当需要比较多种干预措施的效果时，常采用网络Meta分析（network meta-analysis，NMA）的方法。NMA可合并多种干预措施的直接比较和间接比较证据，并可对不同干预措施的治疗效果进行排序，已被广泛应用于评价多种干预措施的疗效[5-7]。由于NMA具有很多优势，许多学者尝试将该方法与诊断性试验Meta分析结合以进行不同诊断试验间的准确性比较。近年来，国外已发表了许多诊断性试验NMA的方法学研究[8-12]，但国内该领域的研究较少。因此，本文在梳理诊断性试验间接比较Meta分析的基础上，分析了诊断性试验NMA的模型及方法学进展，同时介绍了两种实现诊断性试验NMA方法的软件操作步骤，以期为研究人员了解和开展诊断性试验NMA提供参考。

1 诊断试验研究简介

1.1 诊断试验定义诊断试验指临床上用于疾病诊断的各种试验，涉及临床采用的各种诊断手段和方法，它可为疾病正确诊断及其鉴别诊断提供重要依据，同时也可用于判断疾病的严重程度，估计疾病的临床过程、疗效及其预后和检测药物不良反应等。包括：病史和体检所获得的临床资料；各种实验室检查（如生化、血液学、免疫学、病理学检查等）；各种影像学检查（如X线、B超、CT、PET/PET-CT、MRI及放射性核素等）；其他特殊器械检查（如心电图、内镜等）；各种公认的诊断标准（如各种自身免疫性疾病的联合诊断标准等）。

1.2 诊断试验的设计诊断试验的研究类型一般可分为两种：一是诊断性随机对照试验（D-RCT）；二是诊断准确性研究（DTA study），主要采用的研究设计类型为横断面研究、病例对照研究和队列研究[13]。诊断性随机对照试验为患者被随机分配到新诊断方法检查组或旧诊断方法检查组，根据诊断结果接受最佳治疗，通过比较不同诊断方法对患者重要结局的影响来直接推断诊断准确性及其对临床重要结局的影响。诊断准确性试验为患者同时接受新诊断方法（一种或多种）和标准诊断方法（金标准）。随后可评价新诊断方法与标准诊断方法相比较的准确性（第一步）；如果要判断新诊断方法对患者重要结局的影响，研究人员还要基于后续或以前的研究结果，对关于连续治疗和患者（被新诊断方法或标准诊断方法确定为患病或未患病）可能的结局提出假设（第二步）。两种诊断试验的设计流程见图1。

图1 两种诊断试验的设计流程

1.3 诊断试验评价指标诊断试验准确性评价指标包括灵敏度（真阳性率）、特异度（真阴性率）、假阴性率（漏诊率）、假阳性率（误诊率）、似然比（包括阳性似然比和阴性似然比）、诊断比值比、准确度和ROC曲线下面积。临床应用性指标有预测值（包括阳性预测值和阴性预测值）、验前概率和验后概率。

1.4 诊断试验准确性系统评价/Meta分析诊断试验准确性的系统评价/Meta分析是通过系统、全面地搜集诊断试验研究，严格按照预先制定的纳入标准筛选研究，依据国际公认的诊断试验质量评价工具（如QUADAS-2）评价纳入研究质量，并进行定性描述或用合成受试者工作特性曲线（SROC）进行定量分析的一种综合评价诊断试验准确性和重要性的研究方法。诊断试验准确性的系统评价/Meta分析主要有3种模型。

1.4.1 Littenberg-Moses固定效应模型该方法最初由Kardaum等[14]研究者于1990年提出，随后经Littenberg和Moses等[15]研究者对最初提出的模型进行了修正，即Littenberg-Moses模型，成为当前最常用拟合SROC曲线的方法。由于Littenberg-Moses模型拟合的SROC曲线尚存在一些缺点，如没有考虑研究间的变异等，为避免该模型的缺点，可考虑用双变量模型和分层SROC模型。

1.4.2 双变量随机效应模型Reitsma等[16]给出的双变量随机效应模型有两个水平，分别对应研究内和研究间变异。针对指标灵敏度和特异度，在第一个水平上可以认为每个研究的灵敏度和特异度服从一个二项分布，第二个水平上认为每个研究真实的灵敏度和特异度经Logit变换后，服从一个双变量正态分布。双变量模型通过似然函数进行拟合，可获得5个参数估计结果，灵敏度与特异度Logit转换值[E(logit)Sens、E(logit)Spec]和方差[Var(logit)Sens、Var(logit)Spec]及两者的相关系数[Corr(logits)]。

1.4.3 分层SROC模型分层SROC模型由Rutter和Gatsonis[17]提出，是对Littenberg-Moses固定效应模型SROC曲线的扩展，用于合并评价多个诊断试验的灵敏度和特异度这一常用配对指标。在STATA软件中，可通过metandi命令实现，分层SROC的5个参数估计结果分别为：形状参数（Lambda）、诊断比值比（theta）、阈值（beta）以及两者方差（s2theta、s2alpha），其中参数beta估计值及其95%可信区间提示SROC是否对称，Lambda的估计值及其95%可信区间反映诊断试验判别能力。

2 诊断试验准确性间接比较Meta分析

2.1 定义与原理诊断性试验间接比较Meta分析定义为在被比较的诊断性试验间基线特征足够相似且不存在阈值效应的前提下，基于共同的金标准或参考标准，对不存在直接比较的多个诊断性试验进行比较的Meta分析[10,18]。如图2，我们需要比较诊断性试验A和诊断性试验B的诊断价值，然而目前尚无二者之间直接比较的证据，仅有它们与共同的金标准或参考标准C比较的研究，这时需要采用间接比较的方法。在诊断性试验A vs. C和B vs. C具有足够相似性，且不存在阈值效应的前提下，可以通过共同的参考标准C实现诊断性试验A和B诊断性能的间接比较。以诊断比值比（DOR）为例，lnDORac和lnDORbc分别表示诊断性试验A与C和B与C效应量诊断比值比的对数，SelnDORac和SelnDORbc分别表示诊断性试验A与C和B与C效应量诊断比值比对数的标准误，lnDORab'和SelnDORab'分别表示诊断性试验A与B间接比较的效应量诊断比值比的对数和标准误，则：

2.2 方法

2.2.1 SROC曲线法SROC曲线同时兼顾了灵敏度和特异度，可综合反映诊断性试验对目标疾病的诊断价值[18]。对于比较多个诊断性试验的诊断价值，将多个SROC曲线整合到一个图上，通过观察不同SROC曲线下面积来比较各诊断性试验的准确性，越靠近左上角者，其诊断准确性越高。该方法在刘关键等[19]于2003年发表的文章中进行了详细的介绍。目前，可用RevMan软件中诊断性试验模块的“Multiple tests analysis”实现多个诊断性试验的SROC曲线呈现在同一图形中。但该软件并不能提供SROC曲线下面积值和可信区间。如需定量比较各诊断性试验的准确性，可联合使用RevMan和STATA软件来实现。

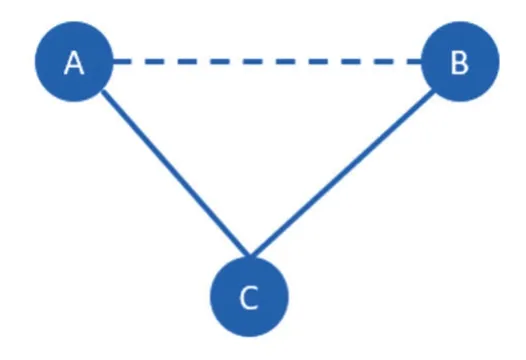
图2 诊断性试验A和B基于共同参考试验C的间接比较示意图

2.2.2 Meta回归方法计算诊断比值比采用诊断性试验Meta回归分析的方法，可计算出诊断性试验的诊断比值的相对比值，从而实现诊断性试验的间接比较。目前可用于实现诊断性试验Meta回归分析的软件有R、STATA和Meta-Disc等软件。利用Meta-Disc软件进行Meta回归分析实现诊断性试验间接比较Meta分析的方法和步骤可参考吴景玲等[18]于2017年发表的文章。

2.2.3 调整间接比较方法对于诊断比值比，可以看作比值比（OR）进行处理，计算各诊断指标比值比的对数值和标准误，采用R软件、WinBUGS软件、STATA软件的Indirect Meta-Analysis命令和ITC软件或采用2.1中的公式均可计算出诊断指标的相对比值及其可信区间。干预类研究调整间接比较的概率排序方法也适用于对诊断性试验的诊断价值进行排序[18]。

3 诊断试验准确性NMA方法学进展

图3呈现了诊断准确性试验NMA的方法学发展过程。

3.1 2014年提出多项式模型Trikalinos等[8]于2014年提出了通过多元正态分布近似的多项式模型对真阳性率和假阳性率联合建模的方法，该方法遵从研究的分组数据，比较了配对设计中针对相同样本的多个诊断性试验，同时考虑了真阳性率及假阳性率在研究内和研究间的相关性。该模型主要适用于诊断性试验对同一样本进行测试的情况，或大量研究报告了几种测试结果的交叉分类数据。但该方法存在许多局限，如不太适用于联合的诊断性试验和诊断试验数量过多的情况。

3.2 2015年提出诊断性试验对比数据模型2015年，Menten等[9]基于随机对照试验混合治疗比较Meta分析的方法提出了一种基于诊断性试验对比数据的方法，该模型直接模拟了多个诊断准确性试验之间的相对logit灵敏度和logit特异度，可以对诊断性试验的直接比较和间接比较进行建模。此外，该模型还可以使用金标准或参考标准的诊断准确性的先验信息和对不完善的金标准或参考标准进行校正。但该方法对金标准或参考标准的依赖性较强，当金标准或参考标准的信息不全或不同研究中不一致，则间接比较的结果不可靠。

3.3 2016年提出四变量线性混合模型和双向ANOVA模型2016年，Dimou等[20]将经典的双变量随机模型Meta分析方法扩展到诊断准确性试验中，用logit灵敏度和logit特异度来比较两个或多个诊断性试验的价值。该方法可以通过封闭形式的表达式来计算研究内的协方差，也可以直接计算灵敏度、特异度、诊断比值比、ROC曲线下面积和SROC曲线的参数，不需要所有的研究同时报告待评估诊断性试验的数据。但随着待评价的诊断性试验的数量增加，模型中的参数数量会迅速增加，可能导致模型收敛出现问题。Hoyer等[21]提出了一种四变量（诊断试验1的灵敏度、特异度和诊断试验2的灵敏度、特异度）线性混合模型来比较具有共同金标准的两种诊断性试验的价值，该方法也考虑了诊断性试验具有多个诊断阈值的情况。但该模型的构建基于每个研究仅提供两个标准的四格表，可能不适用于研究中报告的诊断性试验数量多于两个的情况。此外，该模型没有考虑不同诊断性试验灵敏度和特异度之间的相关性。Nyaga等[10]提出了ANOVA模型来实现诊断性试验的贝叶斯NMA，该方法通过计算logit灵敏度和logit特异度来比较不同诊断性试验的准确性，同时考虑了灵敏度和特异度之间的相关性。该研究还通过实例论证发现基于单个诊断试验的模型比基于对比数据的模型更具优势，因为前者允许对参数进行更直接的解释，利用所有可获得的数据生成更窄的可信区间。

3.4 2018年提出可比较多种诊断试验/多个阈值的双变量NMA模型和诊断性试验NMA贝叶斯分层模型2018年，Owen等[11]使用马尔可夫链蒙特卡洛（MCMC）方法，开发了一个双变量NMA模型，该模型允许对具有多个诊断阈值的多种诊断试验进行比较，并考虑同一研究中多个诊断试验准确性指标之间的相关性。但当研究中不报告诊断试验的阈值时，该模型则不适用。Ma等[22]提出了一种整合缺失的数据框架的贝叶斯分层模型，该模型允许纳入多个诊断试验比较类型、随机和非随机类型的研究，可以合并有金标准和无金标准的诊断试验数据，也可通过SUCRA（surface under the cumulative ranking）对多个诊断试验的价值进行排序，同时考虑了研究间的异质性和诊断试验准确性指标之间的相关性。

图3 诊断准确性试验NMA的方法学进展

3.5 2 019年提出诊断性试验NMA贝叶斯HSROC模型Lian等[23]对贝叶斯HSROC模型进行了扩展，提出了一种可以处理缺失数据的诊断准确性试验NMA方法，该方法可以纳入多种设计类型的数据，同时考虑了金标准的有无、研究间的异质性和诊断试验准确性指标之间的相关性。此外，作者通过模拟研究发现该方法对数据的利用更加充分且比HSROC Meta回归[17]方法更有效。但该模型基于一致性假设，目前该方法还不能解决直接证据和间接证据存在不一致的情况。

4 诊断试验准确性NMA的常见模型与软件操作

目前，诊断试验准确性NMA的方法有很多，本文主要介绍两种可实现诊断性试验准确性NMA的软件操作方法。

4.1 双向ANOVA模型实现诊断性试验NMA

4.1.1 ANOVA模型原理ANOVA模型思想是通过计算诊断准确性指标的相对比值来比较不同诊断性试验的准确性[18]。基于双向ANOVA模型，使用两个独立的二项分布描述患者和健康受试者的真阳性和真阴性，同时考虑了灵敏度和特异度之间的关联性[10,24]。假设存在K个待评价试验和I个研究。在某一个研究i中，（Yi1k，Yi2k）分别指真阳性和真阴性，（Ni1k，Ni2k）为患者和健康受试者，（πi1k，πi2k）分别为“未观察到的”灵敏度和特异度，描述患者和健康受试者之间的真阳性和真阴性的二项分布如下：

其中xi指影响πijk的协变量。

4.1.2 R软件实现ANOVA模型的操作步骤具体步骤：①安装R软件和Stan程序包；②对数据进 行预处理，计算出真阳性人数、真阴性人数、金标准确诊的患者人数和金标准排除的人数，并将诊断试验名称用数字代替。具体数据格式可参考Nyaga等[10]的研究；③读取预处理好的数据；④运行ANOVA模型，具体命令可在Nyaga等[10]研究中获取；⑤将数据与模型关联；⑥加载rstan进行贝叶斯计算，需要设置蒙特卡洛链条数、迭代次数、迭代运算次数等；⑦查看并评估结果，如结果可靠则输出，否则需重新调整参数再次运行模型。

4.2 Owen等提出的诊断性试验NMA模型

4.2.1 Owen等模型原理Owen等的模型是建立在Reitsma等[16]和Sutton等[4]描述的双变量诊断性试验Meta分析模型的基础上。对于第i项研究，假设观察到的真阳性数（tpi）为疾病阳性个体样本（posi）的二项式计数，该信息可以估计诊断试验的灵敏度（sensi）。同样，假设观察到的真阴性数（tni）为疾病阴性个体样本（negi）的二项式计数，该信息可以估计诊断试验的特异度（speci）。则

逻辑回归模型可用于指定灵敏度和特异度。研究间每种诊断试验的灵敏度和特异度可能是相关的。为了解决这种跨研究的相关性，对于第i项研究，从双变量正态分布中得出logit灵敏度[logit (sensi)]和logit特异度[logit (speci)]，其均值等于灵敏度和特异度的合并准确度估计值（μisens，μispec），研究间的协方差矩阵为Σ:

其中τsens和τspec表示对数变换后灵敏度和特异度研究间的标准差（SD），ρ 代表研究间的相关性。为了对同一研究中多个灵敏度和特异度研究内之间的相关性进行建模，可使用方差成分模型[11,25]，将诊断试验阈值组合视为固定效应，而将研究和研究内的诊断试验视为随机效应。研究和研究内的诊断试验嵌套在每个观察中。该模型为：

其中β和δ分别代表诊断试验j和诊断阈值k固定效应下的灵敏度和特异度。c、d、e、f分别代表研究l、研究之间的相互作用l和诊断试验j随机效应下的灵敏度和特异度。所有模型均使用马尔可夫链蒙特卡洛方法在贝叶斯框架中构建。

4.2.2 WinBUGS软件实现Owen等模型的操作步骤①安装WinBUGS软件；②把模型输入WinBUGS软件，加载模型并检查模型有无错误，模型代码可在Owen等[11]研究的附件中获取；③数据写入与加载，数据格式可参考Owen等[11]的研究；④模型与数据编译，设置合适的参数；⑤模型迭代；⑥结果展示与解读。

5 总结

本文在梳理诊断性试验的设计和诊断性试验间接比较Meta分析的原理与方法的基础上，对诊断性试验NMA的方法学进展进行了详细介绍。目前，诊断性试验NMA的模型和方法较多，但每个模型都有其优势和劣势，缺乏一个完美的方法。因此，研究人员在开展诊断性试验NMA时，需综合考虑多种因素，比如数据的类型、诊断性试验的数量、是否报告诊断阈值及诊断阈值的数量等，以选择最为合适的模型。未来的研究人员应继续在诊断性试验NMA的统计方法、结果呈现和报告等方面进行方法学研究，帮助制定者根据不同情境选择更适用的、严谨的诊断性试验NMA模型。