环境激励下人行桥振动时频分析

陈彦江， 郑永瑞， 许维炳*， 苏 鹏， 李娜娜， 闫维明

(1.北京工业大学工程抗震与结构诊治北京市重点实验室， 北京 100124；2.中国地震局地震预测研究所， 北京 100036)

人行桥多用于城市车流及人流较密集的城区，能够有效实现人车分流，缓解交通压力。人行桥多采用钢结构形式，具有外形美观、施工便捷等优点。但人行桥在复杂环境激励下容易产生较大的振动，给行人带来较差的通行体验。英国千禧桥就曾在开放之初因振动较大而被停用[1]。为明晰使用过程中人行桥的动力响应规律和舒适度评价标准，法永生等[2]建立了针对人行桥的烦恼率模型和舒适度评价标准，考虑了行人荷载对人行桥造成的竖向和侧向耦合振动响应，并给出了可行的减振措施和预测结果。施卫星等[3]通过现场实测得到多组人行荷载作用下人行桥的动力响应规律，并进行了舒适度分析，验证了分布式调谐质量阻化器(tuned mass damper, TMD)对人行桥动力响应的调谐减震作用。付一小等[4]对周围交通荷载引起的人行桥振动进行了分析，指出交通荷载激励下人行桥的振动响应较大，在进行人行桥振动控制时应考虑交通激励环境的影响。现有研究成果表明，人行荷载、周围交通荷载以及可能的人行桥周边施工环境荷载对人行桥的振动影响显著，然而多种复杂环境激励下人行桥的动力响应研究仍相对较少，人行桥在不同环境激励条件下的振动响应规律尚不明晰。

人行桥的环境激励包括噪声、临近车辆荷载、人群荷载、风载等随机激励。上述激励条件下，人行桥的动力响应具有幅值小、随机性强、非线性强、信号不平稳等特点。相对于传统的傅里叶变换，Hilbert-Huang变换(HHT)对非线性、非平稳信号的处理具有较大的优势，已在各种领域得到了广泛的应用。张鑫等[5]基于集合经验模态分解(EEMD)和HHT方法对机械轴承的振动信号进行了本征模态函数(intrinsic mode function,IMF)分解，通过Hilbert变换得出了振动信号的边际谱，进而依据边际谱的幅值特性确定了滚动轴承的故障特征，初步建立了机械轴承的故障诊断方法。孙仁等[6]采用HHT对正常人和冠心病人的脉搏信号进行了处理，指出脉搏波形信号随时间和频率动态变化不同分量的主要特征能够反映冠心病害脉搏信号的突变点信息，验证了HHT方法在生物医学领域广阔的应用前景。胡浩然等[7]结合HHT方法和奇异谱分析(singular spectrum analysis,SSA)方法对木结构的基本动力参数进行了识别，指出与HHT方法相比，HHT-SSA结合法能够更好地实现低信噪比信号处理和参数识别。李乔等[8]通过带通滤波和扩展随机减量法，对HHT方法进行改进，编制桥梁结构模态参数识别程序，指出该改进HHT方法能够有效地利用时频域信号识别桥梁结构的频率、阻尼及模态等参数。吴琛等[9]、公茂盛等[10]使用HHT方法对地震信号进行处理，获得了不同地震信号的能量时频分布，量化提取了地震信号的中心频率、瞬时相位、瞬时能量、Hilbert能量、最大振幅对应的时频分布等动力特性。Liu等[11]采用基于地面微波干涉法和ESMD改进的HHT方法，对赵州桥进行了瞬时振动分析，指出该改进方法可以较好评估古桥瞬时动力响应。丁克良等[12]则使用HHT方法对运营期桥梁的动态变形数据进行了处理，指出该HHT方法可用于桥梁健康状况分析，并可为桥梁健康监测提供参考依据。现有研究成果表明，HHT或者改进的HHT方法对不同的振动信号均可进行有效的处理，并可对信号的特征参数进行有效识别。因此，采用Hilbert-Huang变换对人行桥环境激励下的非平稳响应信号进行处理，对明确不同环境激励作用下人行桥的动力响应规律具有显著的实际意义。

鉴于此，现拟采集噪声激励、车辆荷载、行人荷载以及车辆-行人荷载耦合激励条件下某人行桥的动力响应，利用Hilbert-Huang变换对采集的加速度振动信号进行处理，分析不同激励条件下人行桥动力响应的功率谱、本征模态函数(IMF)、边际谱以及Hilbert能量谱等分布特征，旨在明晰不同环境激励作用下人行桥的动力响应规律，以为人行桥的耦合动力响应参数影响规律及控制方法研究所借鉴。

1 Hilbert-Huang变换简介

Hilbert-Huang变换(HHT)是Huang等提出的一种信号处理方法，即利用经验模态分解(empirical mode decomposition,EMD)方法得到信号的IMF，通过对IMF进行Hilbert分析得到信号的Hilbert谱，可以得出信号的时间-频率-能量三维频谱图，以分析信号的时频特性[13-14]。HHT变换算法主要分为EMD分解和Hilbert变换。

1.1 EMD分解

x(t)为原始信号，u(t)为原始信号的上包络线，v(t)为原始信号的下包络线。上下包络线均值为平均包络线m1(t)；然后原始信号x(t)减去上下包络线均值m1(t)得到1个去掉低频的新序列h1(t):

(1)

h1(t)=x(t)-m1(t)

(2)

当h1(t)满足以下条件时，称h1(t)为1个所求的IMF：①极值点数目与过零点数目相等或相差为1；②在任意点，由局部极大值点和局部极小值点构成的两条包络线平均值为0。满足时记为C1(t)，当不满足时重复式(1)、式(2)。将C1(t)从原始信号中进行分离，得到二者的残余项r1(t)：

r1(t)=x(t)-C1(t)

(3)

利用式(1)～式(3)对ri(t)进行n-1次重复处理，直到rn(t)变为单调函数或常数，得到残余项rn(t)。此过程中，可得到n个IMF，且n个IMF与残余项之和即为原始信号，可表示为

(4)

1.2 Hilbert变换

对得到的IMFCn(t)进行Hilbert变换：

(5)

式(5)中：P代表柯西主值。

建立解析信号：

(6)

得到瞬时振幅，瞬时相位：

(7)

(8)

进一步求得瞬时频率：

(9)

然后得到Hilbert谱H(w，t),对其积分得到Hilbert边际谱h(w)：

(10)

最后利用Hilbert振幅的平方对时间积分，得到Hilbert能量谱：

(11)

2 人行桥实测结果

2.1 工程简介

以北京市某人行桥为研究对象，其立面图如图1所示。该桥为三跨连续梁，跨径组合为6.5 m+29.5 m+6.5 m，主梁采用单箱双室钢箱梁形式，桥面宽2.80 m，梁高0.98 m，钢箱梁截面如图2所示。

图1 桥梁立面图Fig.1 Elevation of the pedestrian bridge

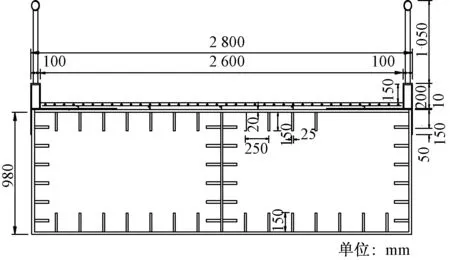
图2 钢箱梁截面图Fig.2 Steel box girder section

2.2 测点布置及数据采集

为了分析不同环境激励下人行桥的竖向振动响应，分别在人行桥第二跨支点截面、1/4截面、1/2截面、3/4截面处布置991B加速度传感器，如图3所示，使用IMC动态采集系统对加速度信号进行采集，采样频率为1 000 Hz。

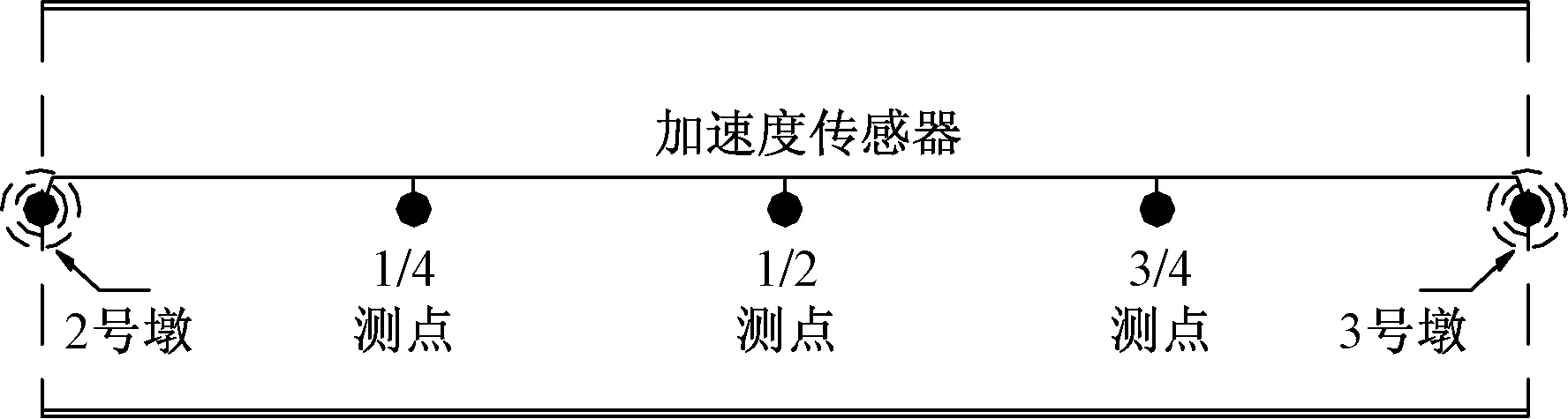
图3 传感器布置图Fig.3 Layout of sensor

图4给出了人行桥第二跨跨中截面在噪声激励、车辆荷载、行人荷载及车辆-行人荷载耦合作用的加速度时程曲线。表1给出了其振动信号的平均幅值(加速度信号的绝对平均值)和脉冲指标(加速度响应峰值和其绝对平均值之比)，其中平均幅值表示振动信号的强弱，脉冲指标可以反应信号的脉冲特性。

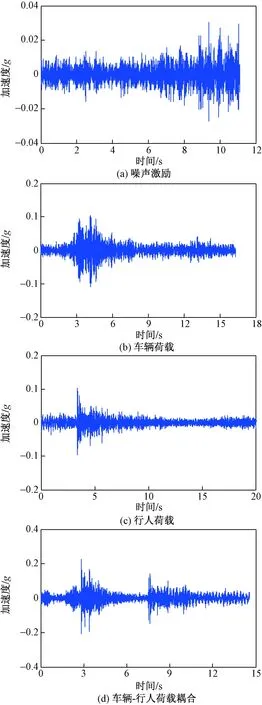
图4 加速度时程曲线Fig.4 Acceleration time history curve

由图4可知，噪声激励振动信号较为平稳，车辆荷载对人行桥振动影响较大，车辆-行人荷载耦合作用时人行桥振动最显著。对比表1中的数据可知，四种工况下加速度幅值不断增大，脉冲指标呈逐渐增加的趋势。

表1 绝对平均值和脉冲值Table 1 Absolute average and pulse value

注：g为重力加速度。

3 桥梁动力响应分析

3.1 功率谱分析

经计算人行桥的一阶竖向基频为4.98 Hz，满足规范要求的3.0 Hz的设计要求[15]。图5给出了人行桥跨中截面在不同环境激励时的加速度响应的功率谱图。

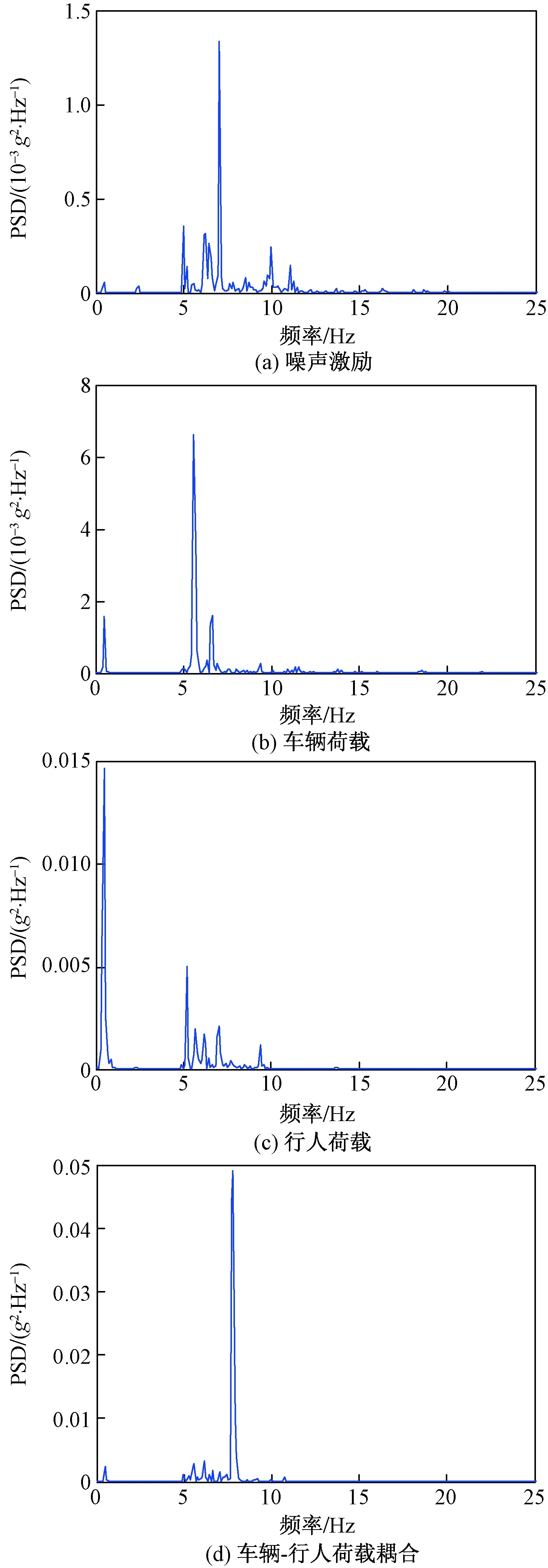
图5 四种工况的功率谱Fig.5 Power spectrum of four operating cases

由图5可知，四种工况的功率谱频率大都集中在5～10 Hz，但是功率谱密度(PSD)峰值存在较大差异，工况1至工况4峰值不断增大，而且峰值不断向高频段转移。工况3峰值频率为0.49 Hz，与0.5 Hz的行人步频基本一致，噪声激励下的峰值较小，车辆-行人荷载耦合作用的峰值最大，同时频率最高，说明车辆-行人荷载耦合作用对人行桥的振动响应最显著。

3.2 EMD分析

四种工况的振动信号经过EMD分解得到11个本征模态函数IMF1～IMF11，如图6所示。

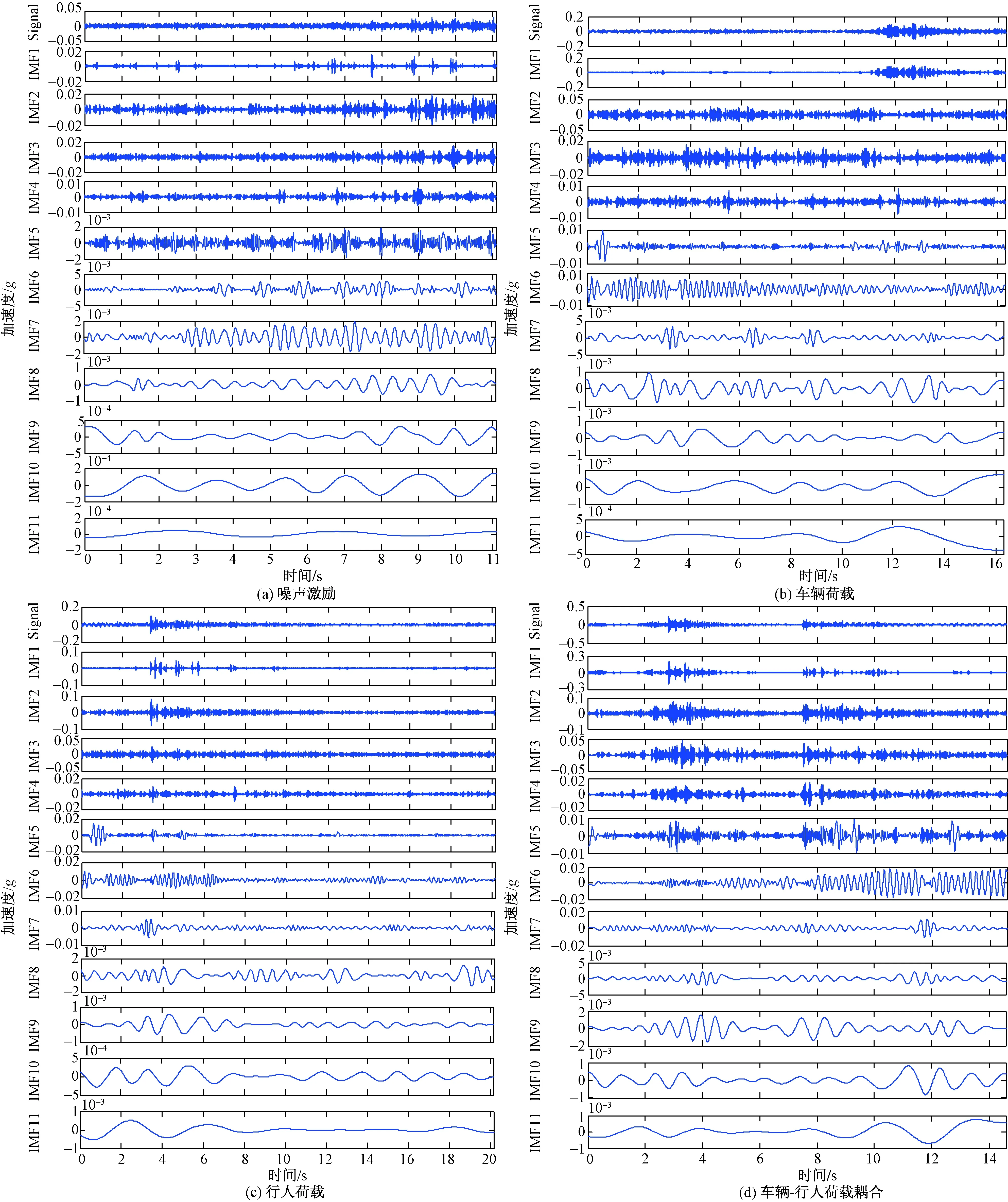
图6 四种工况的EMD分解结果Fig.6 EMD decomposition results of four case

通过计算每个IMF的方差贡献率和相关系数，对信号成分进行分析，以此衡量其相对于整体的重要程度，确定不同环境激励下桥梁振动信号的主要成分。方差贡献率的计算公式为

(12)

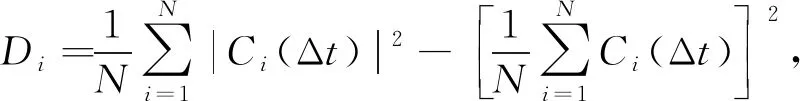
(13)

式(13)中：x(t)为初始振动信号；Ci(t)为IMF分量。图7为四种工况下每个IMF的相关系数和方差贡献率。

由图7可知，随着IMF分量的增加，方差贡献率和相关系数逐渐减小。四种工况的前五阶IMF的方差贡献率及相关系数之和都大于0.95，说明其包含了振动信号的所有特征，且贡献率和相关系数变化趋势一致，都呈逐渐减小的趋势。

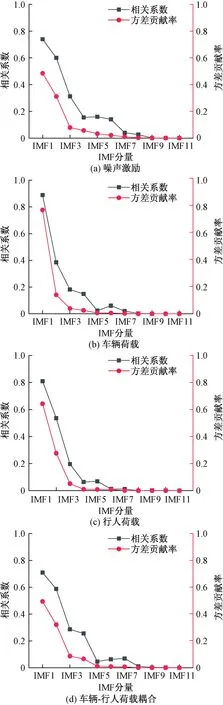
图7 IMF分量的相关系数和方差贡献率Fig.7 IMF component correlation coefficient and variance contribution rate

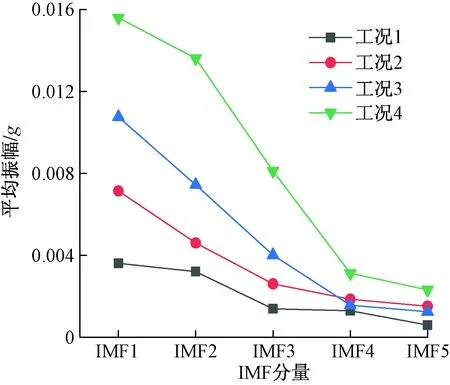
图8 前五阶IMF振幅均值Fig.8 The first five order of IMFs amplitude mean

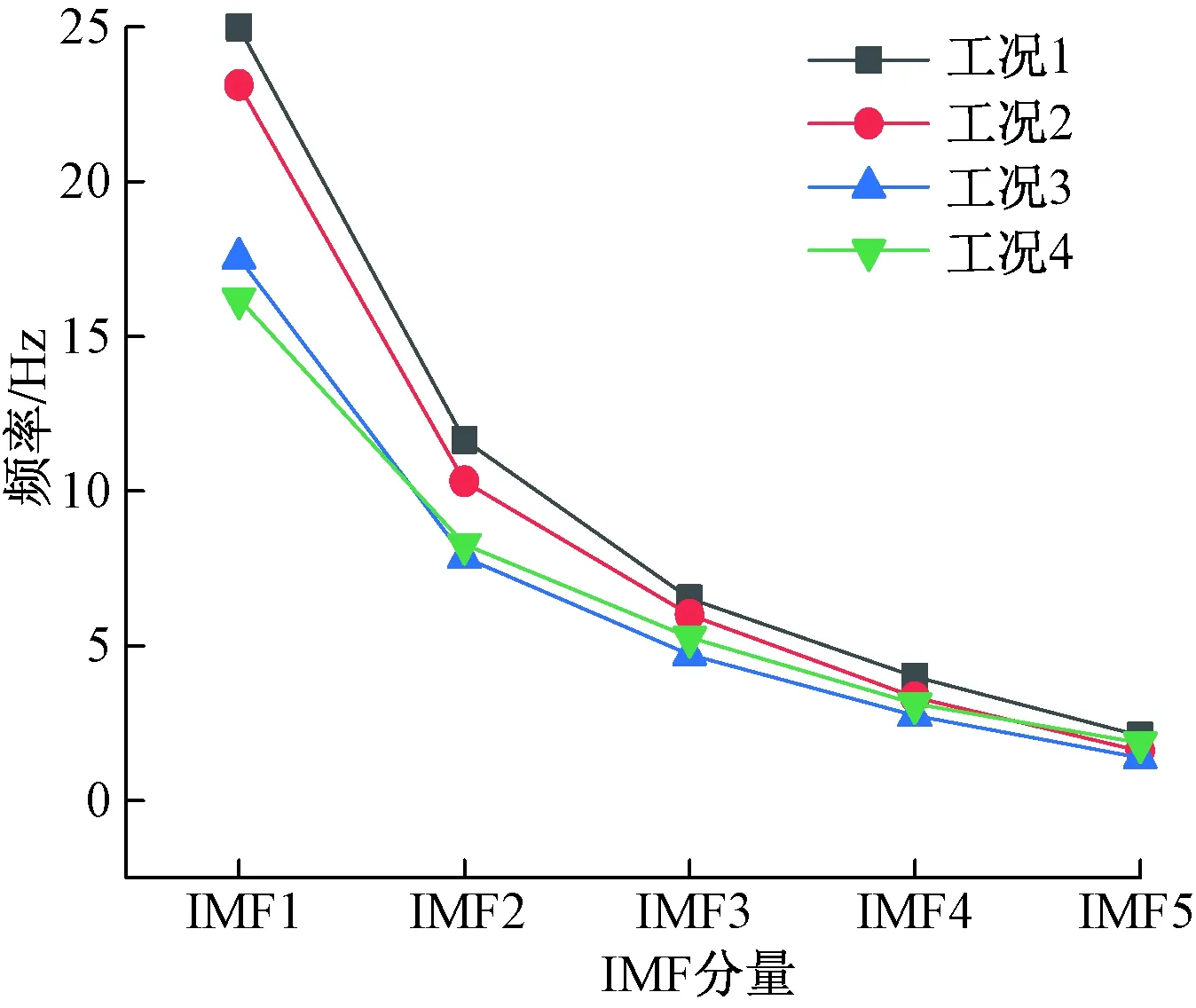
图9 前五阶IMF频率均值Fig.9 The first five order of the IMFs frequency mean

因此以前五阶IMF作为桥梁振动信号的主要成分，计算了四种工况前五阶IMF的瞬时振幅和瞬时频率均值。图8、图9分别给出了其瞬时振幅，瞬时频率均值。由图8可知，四种工况前五阶IMF振幅均值呈逐渐减小的趋势，对于同一阶IMF分量，工况1至工况4的振幅均值逐渐增大，车辆-行人荷载耦合时IMF1分量振幅均值为0.015 6。由图9可知，前五阶IMF分量的频率逐渐减小，对于同一阶IMF分量，工况1至工况4分量的频率逐渐减小。车辆-行人荷载耦合时IMF1分量频率均值较其他工况最小，为16.21 Hz。不同环境激励振幅均值越大，频率均值越小，逐渐向结构的一阶基频靠近，此时桥梁振动响应越大，所携带的能量信号越高。

3.3 能量谱分析

利用Hilbert变换得到其关于时间、频率和能量的分布关系，从能量的角度分析四种不同的环境激励对人行桥的振动响应规律。分别计算了人行桥在噪声激励、车辆荷载、行人荷载及车辆-行人荷载耦合作用下的加速度响应的边际谱和三维联合时频图，如图10所示。

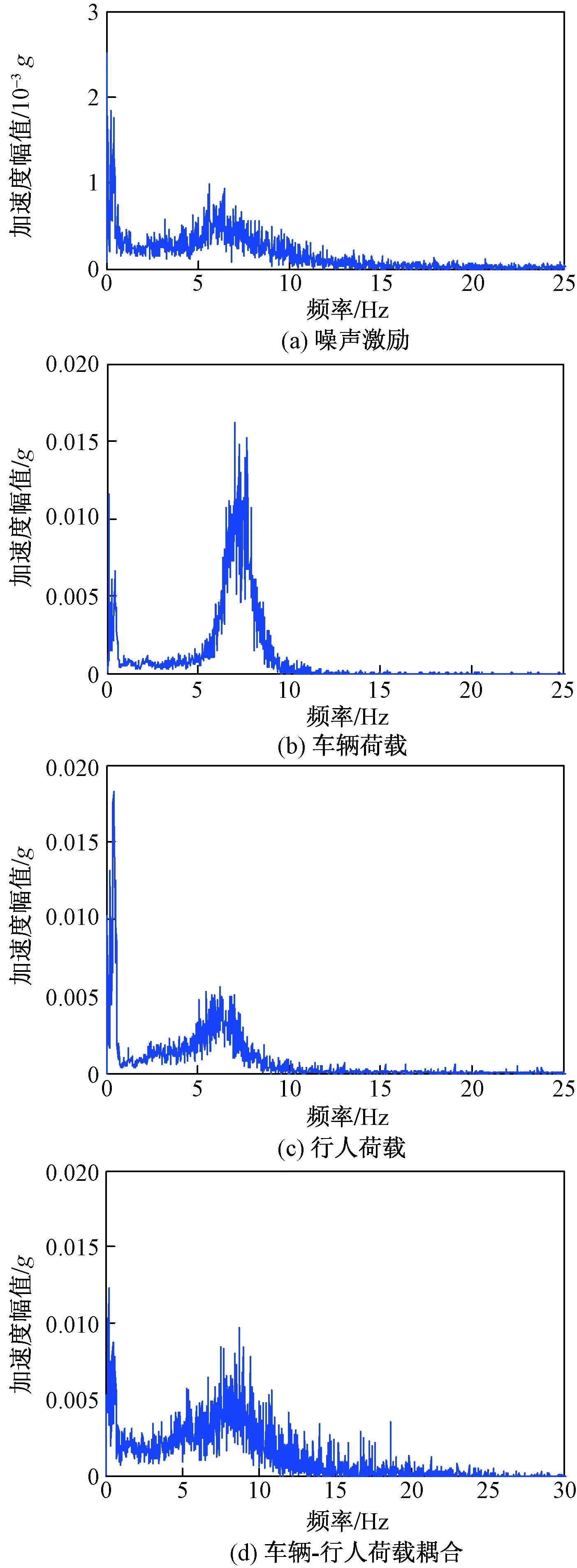
图10 四种工况的边际谱Fig.10 Marginal spectrumof four operating cases

由图10四种工况的边际谱可以得出：边际谱的峰值分布差异很大，主要集中在5～10 Hz，噪声激励的峰值最小，车辆荷载的最大，由于车辆荷载的脉冲效应显著，导致车辆荷载的边际谱峰值较大，车辆-行人荷载耦合的边际谱较小，频率分布广泛，这是由于车辆-行人荷载耦合作用的随机性造成的。图11给出了四种工况的三维联合时频图。

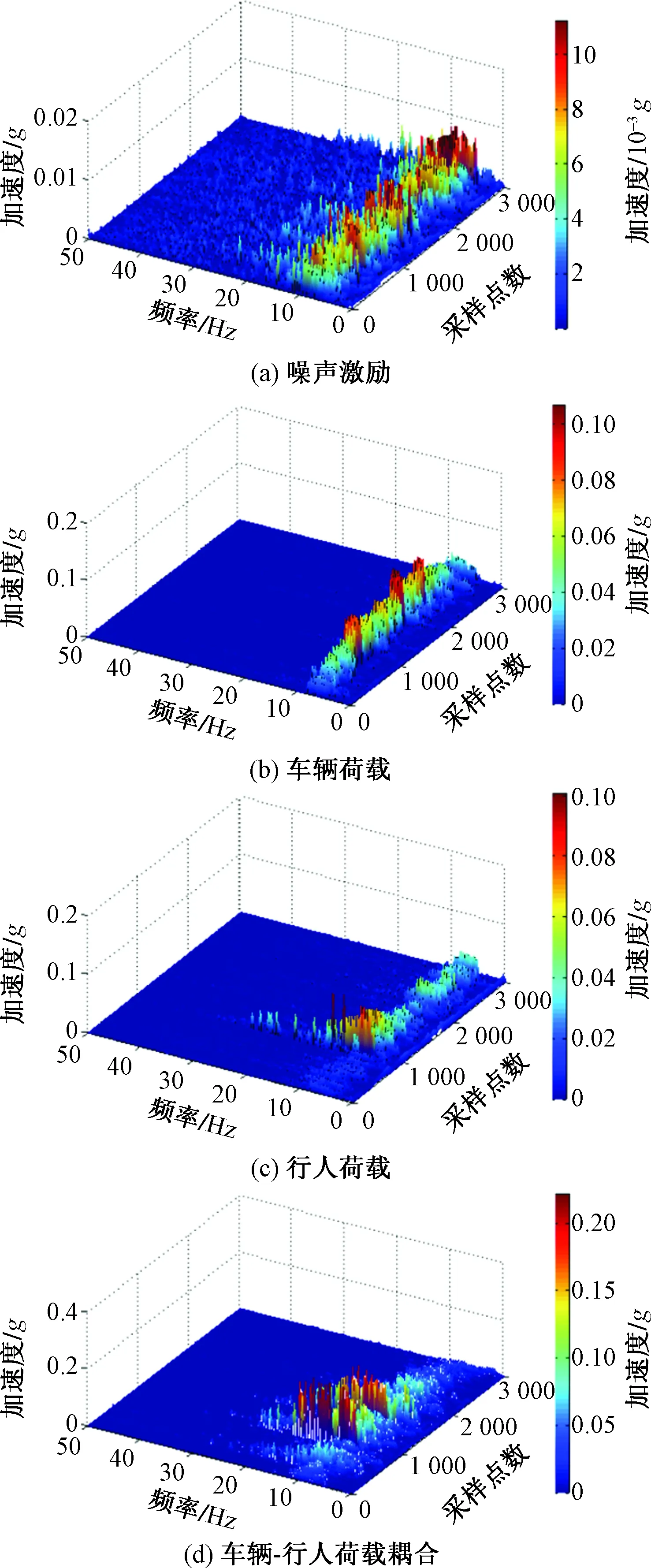
图11 四种工况的三维联合时频图Fig.11 Three-dimensional joint time-frequency diagram of four operating case

由图11可知，四种工况下频率分布在5～20 Hz。在噪声激励作用下，能量幅值较小，频率分布较为广泛，能量分布较为均匀。相对于噪声激励，车辆荷载作用的能量幅值增大，频率分布范围变小；行人荷载作用能量幅值增大，能量峰值逐渐向高频段转移；车辆-行人荷载耦合作用下，能量幅值较大。对于人行桥，不同的荷载对于桥梁振动响应具有显著影响，其振动信号的频率分布，能量分布也存在较大的差异。通过引入能量熵值的概念，来分析能量分布随不同荷载的变化规律。

对采集到的振动信号各个IMF进行能量计算。假设残余分量的能量可以忽略，由于EMD分解具有正交性，所有IMF分量的能量之和等于初始信号的总能量。不同IMF分量包含不同的频率，对应不同的能量E1、E2、…、En，形成振动信号在不同频域对应的不同能量分布，得到不同能量信号熵值[16]，如式(14)所示，表2计算了不同工况的熵值。

表2 四种工况的能量熵值Table 2 Energy entropy valuesof four operating conditions

(14)

式(14)中：pi为不同IMF能量对应振动信号总能量的权重。

对比表2和图11可知，工况1作用下人行桥振动信号的频率分布范围较广，能量分布不确定性增大，能量熵值较大。随着激励荷载幅值的增大，如工况2，结构动力响应频率分布较为集中，多数峰值

点集中在8 Hz附近，能量分布不确定性减小，能量熵值减小。可见频率分布广泛则能量分布不确定性增加，熵值越大；频率分布集中，能量分布均匀，熵值越小。通过能量熵可以直观地看出振动信号的能量分布和频率分布之间的关系。

4 结论

通过对某人行桥分别在噪声激励、车辆荷载、行人荷载及车辆-行人荷载耦合四种工况作用下的加速度响应进行了时频分析和能量分析，得出以下结论。

(1)四种工况下的功率谱主要分布在5～10 Hz范围之间，信号平均幅值逐渐增大，脉冲值呈逐渐增大的趋势，振动响应越强，功率谱峰值不断向高频段偏移。

(2)对每个IMF的方差贡献率和相关系数分析，前五阶IMF分量均超过0.95，包含了振动信号的全部特征。分析了前五阶IMF的瞬时振幅和瞬时频率均值，都呈逐渐减小的趋势。对于同一阶IMF，工况1至工况4振幅逐渐增大，频率逐渐减小，说明桥梁振动响应越大。

(3)由于车辆荷载作用的脉冲值较大，导致其边际谱峰值较高。工况1至工况4三维联合时频图峰值逐渐增大，频率分布范围有所不同，噪声激励分布最广泛，车辆荷载分布相对集中。

(4)引入能量熵值来表示能量分布和频率分布的变化规律。噪声激励时频率分布范围越大，能量分布不均匀，熵值越大。车辆荷载作用下能量分布均匀，熵值越小。