随机观察时间对偶风险模型中的期望折现罚函数

江五元,黄 俊

(湖南理工学院数学学院,湖南岳阳414006)

§1 引 言

在保险数学文献中,许多研究者研究了经典风险模型的对偶模型.如[1]研究了带红利界策略的对偶模型中的期望折现红利支付,当收益为指数分布或混合指数分布时得到了明确的计算公式,并证明了在对偶模型中,最优红利界独立于初始资本.[2]考虑了扩散干扰对偶模型,分析了红利界的最优问题.[3]将经典对偶风险模型推广到广义Erlang(n)对偶模型,得到了破产时间的明确表达式.[4]研究了带利率的复合资产模型,得到了生存概率与破产概率的积分-微分方程.[5]讨论了负风险和的更新风险模型的破产概率.

考虑对偶风险模型

其中u>0为初始资本,c>0表示单位时间的消费支出,{S(t):t≥0}为到时间t的总收入.该模型可以模拟以研究和开发为主营业务的公司的资金流,同时也可以应用于人寿保险公司.对对偶模型的进一步了解,读者可以参考相关文献,如[6-8].

已有文献对对偶模型的研究都假设公司盈余是连续观察的,实际上公司财务状况应是每隔一定的时间段才进行观察,如财务报表每年或每季度发布一次.基于此,本文研究文献[9]的对偶情形,考虑了财务观察时间间距分别服从指数分布和Erlang(n)分布的对偶风险模型中的期望折现罚函数.同时也将[10]的指数分布观察时间间距推广到Erlang(n)分布的情形.

U(k)=U(k−1)−cιk+[S(ϑk)−S(ϑk−1)],k=1,2,···,

其中,U(0)=R(0)=u.破产时间记为T=ϑk∗,k∗=inf{k≥1:U(k)<0},即当盈余为负时的首次观察时间.因此在模型(1.1)中,当盈余为负时,如果没被观察到破产仍然没有发生.

若破产发生,在最近一次观察时间的破产前盈余为U(k∗−1),破产赤字为|U(k∗)|.破产概率为

ψ(u)=Pr(T<∞|R(0)=u)=E{I(T<∞)|U(0)=u},

其中I(A)表示集A的示性函数.设δ≥0为折现系数,期望折现罚函数为

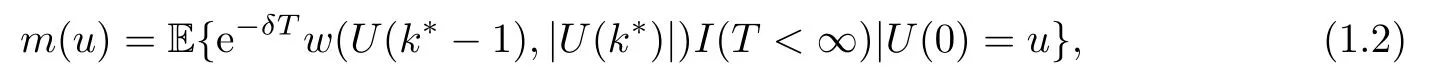
其中惩罚函数w(x1,x2)为破产前盈余U(k∗−1)和破产时赤字|U(k∗)|的二元函数.

§2 观察时间间距服从指数分布

本节假设惩罚函数仅仅依赖破产前赤字,即w(x1,x2)=w2(x2),且观察时间间距服从参数为γ的指数分布.

2.1 期望折现罚函数的积分-微分方程

在充分小的时间区间(0,†)内,有且仅有下列四种情形发生:(1)没有观察和收入到达;(2)有一次观察发生但没有收入到达;(3)有一次收入到达但没有观察发生;(4)两个或以上事件发生.利用全概率公式,有

因为当盈余小于0时,可能没被观察到,故函数m(u)的自变量范围u∈R.对(2.1)关于†求导,令†→0,得

2.2 指数收入时的显式解

§3 观察时间间距服从Erlang(n)分布

本节假设收入量为任意分布,观察时间间距ι服从Erlang(n)分布,密度函数

3.1 两次观察之间的折现增量

3.2 期望折现罚函数的显式解

将(3.17)与[9]中的Lundberg方程(3.25)进行比较,则关于变量µi的方程(3.17)恰有nh个非负实部的根和n个负实部的根.假设limu→∞m(u)=0,当µi≥0时,有Ci=0,i=1,2,···,n(h+1),利用(3.18)可以决定Ci,i=1,2,···,n(h+1).因此m(u)可以通过(3.13)计算.

例1(观察时间间距服从指数分布时的破产概率)考虑对偶风险模型(1.1),假设观察时间间距ι与收入量X均服从指数分布,期望分别为1/γ,1/µ.设定µ=1,λ=2和c=1,显然正的安全负荷条件满足.

在(2.17)中,取δ=0,可计算破产概率ψ(u).图1显示γ取不同值时的ψ(u).最上边的实线表示连续观察时的破产概率,u=0为其不连续点.图1表明对于固定的u,破产概率随γ的增加而增加.显然γ越大表示观察时间间距越短,导致观察到破产的机会越大.

图1 γ取不同值时的ψ(u)

例2(观察时间间距服从Erlang(n)分布时的破产概率)假设对偶模型(1.1)的观察时间间距服从Erlang(n)分布.收入量服从指数分布,密度函数为f(x)=µe−µx,拉普拉斯变换为.取µ=1,λ=2,γ=2和c=1.当n=3,5时,图2表明对固定的u和γ,破产概率随n减小而增加.因为n越小表示观察次数越多,从而观察到破产的机会越多.

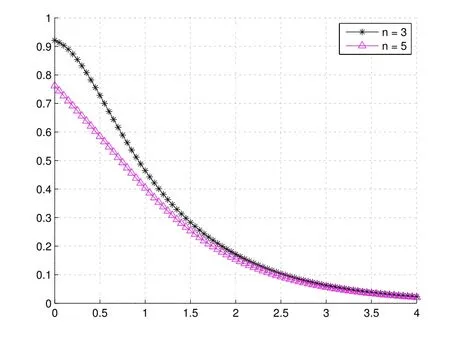
图2 n取不同值时的ψ(u)

本文研究了随机观察时间的对偶风险模型中的期望折现罚函数,当随机观察时间分别为指数分布和Erlang(n)分布时,建立了期望折现罚函数所满足的积分-微分方程.假设惩罚函数仅依赖于破产赤字,即w(x1,x2)=w2(x2),收入分布具有有理形式Laplace变换时,得到了期望折现罚函数的显式解.本文研究的是文献[9]中风险模型的对偶模型,并将文献[10]研究的指数分布随机观察时间推广到Erlang(n)分布情形.值得提出的是,为了得到期望折现罚函数的显式解,假设惩罚函数仅依赖于破产赤字,对于惩罚函数同时依赖于破产前盈余和破产时赤字的情形则有待进一步研究.