Tweedie复合泊松回归模型的Bayes估计和影响分析

2020-12-15段星德罗露璐张文专

高校应用数学学报A辑 2020年4期

段星德,张实,罗露璐,张文专

(贵州财经大学数统学院,贵州贵阳550025)

§1 引言

Tweedie复合泊松分布常用来分析由零和正的连续数据所构成的半连续型数据,这类数据广泛存在于精算科学(比如:保险公司对不同个体的赔偿金额),环境科学(比如:一段时间某个地区的降雨量)等研究领域中.对半连续数据建模常见的有两类方法,第一,两部分模型,即混合Bernoulli分布和Gamma分布或者Lognormal分布,常被用来分别处理零数据和正的连续数据两部分(Fernandes等[1],Piantadosi等[2]),然而这种分割处理方法常会破坏半连续数据的整体属性(Hasan等[3]).第二,Hasan等[3]以及Hasan和Dunn[4-6]发展了Tweedie复合泊松模型来对降雨量和降雨发生率联合建模.进一步,针对Tweedie复合泊松模型的统计推断问题,Smyth和J∅rgensen[7]研究了Tweedie复合泊松模型的均值和散度参数的联合建模问题以及约束极大似然估计方法;Dunn和Smyth[8-10]提出了不同的数值方法去逼近Tweedie复合泊松分布的密度函数并给出了R软件包;Peters等[11]给出了Tweedie复合泊松模型的极大似然估计和基于Markov Chain Monte Carlo(简称MCMC)模拟技术的Bayes估计;Zhang[12]基于Monte Carlo EM和MCMC等算法研究了Tweedie复合泊松混合效应模型的估计问题;Qian等[13]基于分组弹性网估计技术研究Tweedie复合泊松模型的变量选择问题;Yang等[14]把梯度提升树算法应用到Tweedie复合泊松模型中并用来预测半连续保险数据;Bonat等[15]提出两类拟似然和伪似然方法对Tweedie复合泊松模型进行统计推断.但据作者所知,基于Bayes数据删除方法对Tweedie复合泊松模型的统计诊断分析还没得到研究.

近几年来,基于Bayes数据删除影响诊断以引起大量研究者的关注.特别地,Cho等[16]基于K-L差异统计量的Bayes数据删除影响测度来研究生存模型的统计诊断问题;Zhu等[17]系统研究了三种Bayes数据删除影响测度的统计性质,并把这些统计诊断方法应用于复杂统计模型中;Jackson等[18]提出两类基于MCMC算法的方法去逼近Bayes数据删除影响测度;Duan和Tang[19]对广义部分线性混合效应模型建立起一套基于Bayes数据删除影响诊断方法来评价模型对于删除一个数据点或数据组的敏感性.因此,本文将在Bayes估计的基础上基于Bayes数据删除影响方法来研究Tweedie复合泊松模型的统计诊断问题.

§2 模型

本节首先介绍泊松-伽玛复合分布,即Tweedie复合泊松分布,其次引入它们所对应的广义线性模型:Tweedie复合泊松回归模型.

2.1 Tweedie复合泊松分布

如果一个随机变量Y服从泊松-伽玛复合分布,则它可以表示为如下的随机表达式.

其中N为服从均值参数为λ的泊松分布的随机变量;给定N的条件下,Xi(1≤i≤N)独立同分布,服从均值为αγ,方差为αγ2的伽玛分布;且N和Xi相互独立.另外当N=0时,有Y=0.进一步,P(Y=0)=P(N=0)=exp(−λ).

根据Jørgensen[20],Tweedie复合泊松分布是指数散度分布族的一类特殊分布,而指数散度分布族的概率密度函数可表示为

其中a(·)和κ(·)是已知函数;θ为定义在R=(−∞,∞)上的参数,φ>0为散度参数.根据指数散度分布族的性质有:

其中κ0(θ)和κ00(θ)是分别关于θ的一阶和二阶导数.根据(2.1)和(2.2),可得两组参数之间的关系:

显然参数p的取值范围为(1,2).因此把一个随机变量Y服从泊松-伽玛复合分布记为Y∼Twp(µ,φ),其中E(Y)=µ,var(Y)=φµp,p∈(1,2)称之为幂指标参数.

为了对模型进行统计推断,需要推导出泊松-伽玛复合分布的概率密度函数,即写出(2.2)式中所对应的具体表达式.尽管泊松-伽玛复合分布的概率密度函数没有显示表达,但涉及到的模型可以通过Y和N的联合概率密度函数进行统计推断,其中N可视为潜变量.根据(2.1),Y和N的联合概率密度函数可以表示为

2.2 Tweedie复合泊松回归模型

设yi,i=1,2,···,m是响应变量Yi的第i次观测值,Y1,···,Ym相互独立,则Tweedie复合泊松回归模型表示为

其中xi=(xi1,xi2,···,xiq)T∈Rq是q维固定效应协变量,β为对应的q维待估的未知参数.另外

§3 模型的Bayes分析

令

在统计推断过程中,可把潜变量N视为缺失数据,而Y仍然为观测数据,(Y,N)视为完全数据.为了获得模型参数的Bayes估计,考虑参数θ的基于完全数据(Y,N)的后验分布.类似于Zhang[10],Y和N的联合对数似然函数为

因此参数θ基于完全数据(Y,N)的后验分布为

其中p(θ)为参数θ的先验概率密度函数.进一步,根据Zhang[10],θ的先验分布可假定为

其中β0,Σ0,φ0为事先给定的超参数,U(·)表示均匀分布.

3.1 条件分布和Gibbs抽样

为了进行Bayes推断,用Gibbs抽样技术从联合后验分布p(θ,N|Y,X)中抽取所需的随机样本,并基于此随机样本对参数θ进行Bayes推断.

由(3.1)-(3.3)式可知,给定θ,Y,X下N的对数条件分布可以表示为

于是有

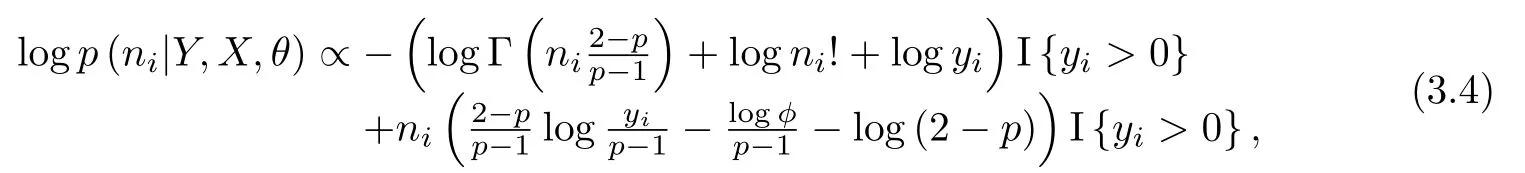
其中I{·}表示示性函数.由于{yi=0}与{ni=0}是两个等价事件组,即当yi=0时隐含着ni=0,因此基于条件分布(3.4)式进行抽样时只需对ni>0的情形进行抽样.

由(3.1)-(3.3)式可知,给定N,Y,X,β,φ下β的对数条件分布可以表示为

利用Gibbs抽样技术对上述条件分布进行抽样时涉及到的条件分布都是一些非标准分布且非常复杂,因此将选择一些合适的,有针对性的MH算法来进行随机抽样.

3.2 MH算法

为了实施MH算法,假设潜变量ni和参数θ的当前迭代值为和θ(t),新的随机样本和θ∗服从如下建议分布:

3.3 Bayes估计

基于上述Gibbs抽样和MH算法的混合算法获得随机样本,就可以得到θ=(β,φ,p)的联合Bayes估计及其对应的标准差.

设

是来自于联合后验分布p(θ,N|Y,X)的随机样本,则θ=(β,φ,p)的Bayes相合估计可以表示为

类似地,参数θ的后验协方差矩阵var(θ|Y,X)的相合估计可以通过它们的随机样本的样本协方差矩阵得到,即

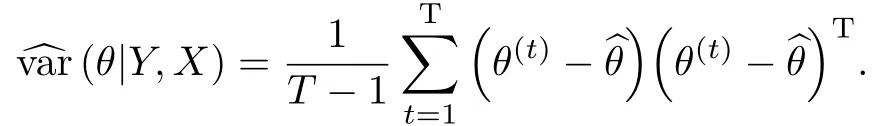
另外可以通过随机样本序列的样本协方差矩阵的对角线元素来估计对应的标准差.

§4 Bayes数据删除影响测度

在贝叶斯框架下,将基于Tweedie复合泊松回归模型引入两类Bayes数据删除影响测度.首先引入记号,用{yi,xi}表示第i个数据点,D={Y,X}为完全数据集,表示删除第i个数据点后剩余的数据集;令参数向量θ=(β,φ,p).

为了度量数据点{yi,xi}对参数θ的联合后验分布的影响程度,根据Cho等[16]和Zhu等[17]的工作,首先引入如下的第一类型Bayes数据删除影响测度:

其中p(θ|D)和p(θ|D[i])是θ关于数据集D和D[i]的后验分布.该影响测度Dφ(i)用来度量数据点{yi,xi}删除前后的影响程度,若它的估计值比较大,则对应的数据点{yi,xi}可能是强影响点或异常点.

另外为了度量数据点{yi,xi}对θ的后验均值的影响程度,根据Zhu等[17]的工作,定义如下的第二类型Bayes数据删除影响测度.

在实际计算中,通常使用参数θ的样本后验协方差矩阵的逆矩阵来估计正定阵Wθ.同理若CM(i)的估计值比较大,那么所对应的数据点{yi,xi}可能对参数θ的后验均值的估计产生较大的影响;因此数据点{yi,xi}可能被诊断为强影响点或异常点.

在计算这两类影响测度Dφ(i)和CM(i)的过程中,发现需要计算所涉及到的后验分布p(θ|D)和p(θ|D[i]),但所考虑的模型涉及到潜变量N的处理,这给计算带来一定的困难.为了有效的处理潜变量N,发展了以下一些简单有效的计算公式.

首先根据Zhu等[17]的计算方法,令

pi(θ)=p(Y|X,θ)/p(Y[i]|X[i],θ)=p(Yi|Xi,θ).

通过一些计算可得到如下的表达式:

因此第一类型Bayes数据删除影响测度可以简化为

Dφ(i)=logEθ|D{pi(θ)}−1+Eθ|D{logpi(θ)},

这种影响测度也称之为K-L差异测度.进一步,可基于上述的MCMC算法从从后验分布p(θ|D)中进行抽取样本来计算该影响测度.

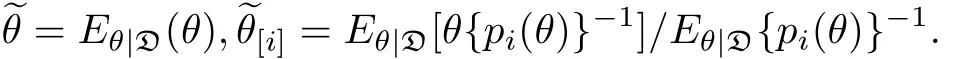
同样利用上述的MCMC算法从后验分布p(θ|D)中抽取样本来计算后验均值以及θ的后验协方差矩阵Wθ,从而可计算出影响测度CM(i)的值.总之,计算上述两类Bayes数据删除影响测度的关键所在是计算pi(θ)的值.根据pi(θ)的定义,可得

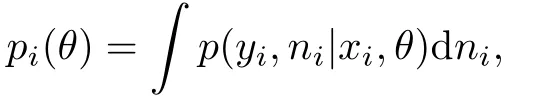
这就意味着对存在潜变量的模型中计算pi(θ)是繁琐的.尽管这给计算影响测度Dφ(i)和CM(i)带来困难,但可利用下面的数值方法来计算pi(θ).具体地,可以利用Monte Carlo方法来逼近pi(θ),即

其中若yi=0时,所对应的潜变量ni的取值为0;若yi>0时,所对应的潜变量ni的随机样本

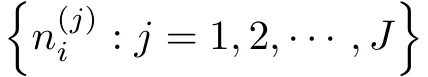
从零截断泊松分布f(ni;λ|ni>0)中产生,这里λ是所对应泊松分布的均值参数,它可通过潜变量N的样本均值来进行估计.在下一节的模拟研究和实例分析中,取J=200或更大的数值.

§5 模拟研究

在第一个模拟研究中,假设响应变量{yi,i=1,2,···,m}服从Tweedie复合泊松分布,即Yi∼Twp(µi,φ);模型的系统部分表示为:

log(µi)=β1x1+β2x2+β3x3+ ···+β10x10,

其中样本量m=150,协变量xi∼N(0,1),i=1,2和xi∼N(0,0.25),i=3,4,···,10,且这10个协变量是相互独立的,回归参数向量β的真值为

βT=(β1,β2,β3,β4,β5,β6,β7,β8,β9,β10)=(0.85,0.85,1,1,1,1,1,1,1,1),

散度参数φ的真值为φ=2,幂指标参数p的真值为p=1.6.

为了研究参数分布的不同先验信息对Bayes估计的影响,将考虑如下三种不同的超参数设置.

类型I:参数β的先验分布的超参数β0的取值为β的真值,即

β0T=βT=(0.85,0.85,1,···,1),

协方差阵Σ0=0.25I10,I10表示10阶单位阵.这种情形可视为参数的先验分布具有良好的先验信息.

类型Ⅱ:设β0T=1.5×βT=1.5×(0.85,0.85,1,···,1),协方差阵Σ0=0.75I10.这种情形可视为具有不准确的先验信息.

类型Ⅲ:设β0T=(0,0,0,···,0),协方差阵Σ0=100I10.这种情形可视为具有无先验信息.

基于上述设计产生的100个模拟数据,用前面提出的Bayes混合算法进行100次重复试验得到参数的联合Bayes估计.这里用计算出的所有参数的EPSR(estimated potential scale reduction)值来判断混合算法中所产生的Markov链的收敛性.在每一次模拟测试中,利用每一个参数的3组不同初值分别产生3条平行的Markov链,并基于每一次迭代值计算出所有参数的EPSR值.在所有模拟测试中,发现所有参数的EPSR值在迭代次数为1000次时均小于1.2,说明模拟研究中的混合算法是收敛的.在本次模拟研究中,利用随机抽取一次模拟测试中12个参数的迭代值进行计算相应的EPSR值,其计算结果见图(1左图).因此在每次重复实验中迭代10000次,为了保证算法的收敛性,丢掉了所有参数的前5000次迭代值,保留后5000次迭代值用来计算参数的Bayes估计.另外在实施MH算法和随机游走MH算法中,选择调节参数

让它们所对应的参数抽样的平均接受率分别为25.7%,29.1%,24.7%,27.7%.表1给出了所有参数θ的相对偏差值(记为RB)、标准差和RMS,其中

在第二个模拟研究中,为了检验协变量出现多重共线性情形时对模型的参数估计的影响情况,在第一个模拟研究的基础上,对协变量进行如下两种假定:

图1 模拟研究中所有参数的EPSR值(左图);实例分析中所有参数的EPSR值(右图)

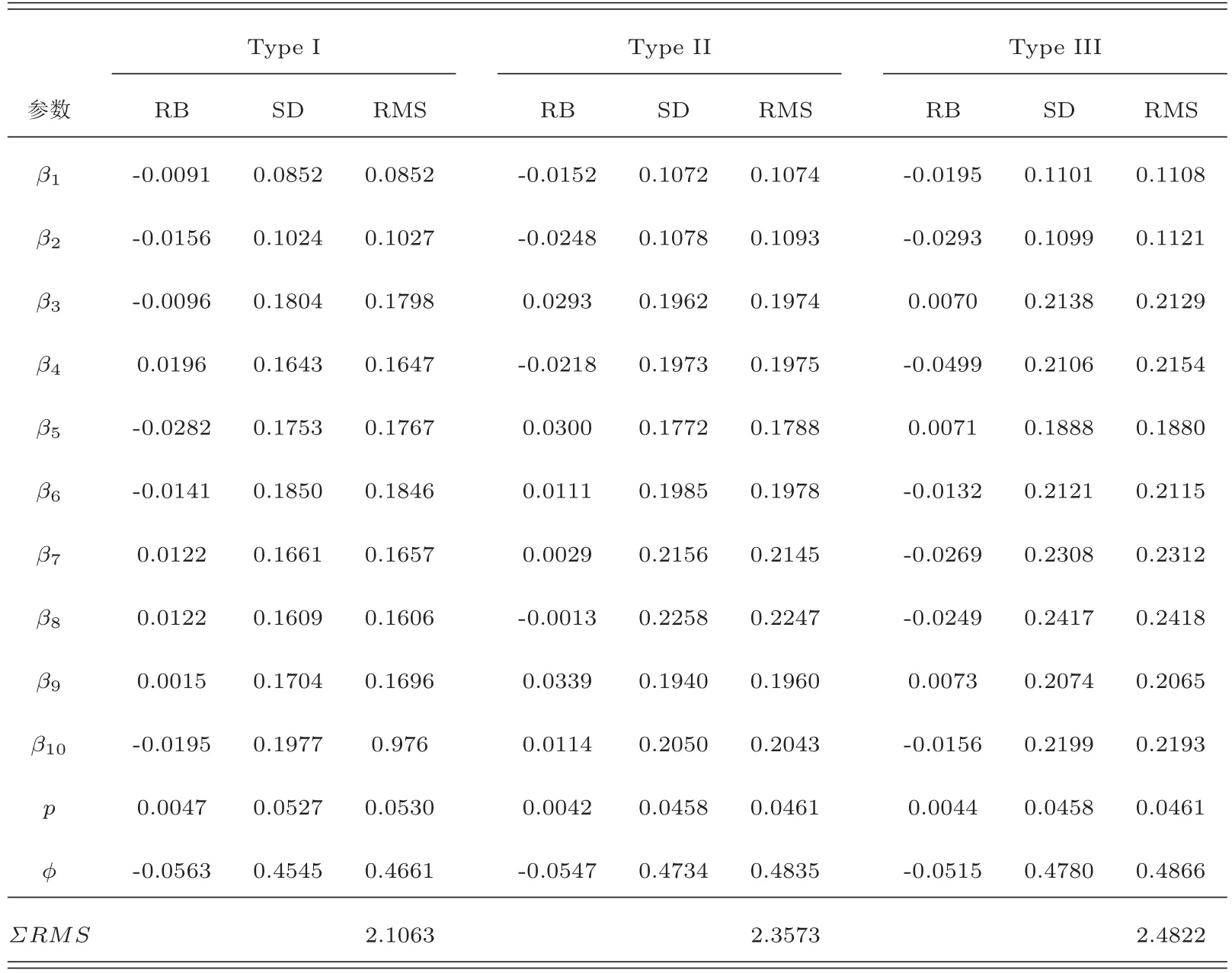
表1 随机模拟研究中未知参数的Bayes估计

(1)协变量

(x1,x2)∼N2(µ0,Σ0);

(其中µ0=(0,0),协方差阵Σ0的元素为0.5|i−j|,i,j=1,2)和xi∼N(0,0.25),i=3,4,···,10;

(2)协变量

(x1,x2,x3)∼N3(µ0,Σ0).

(其中µ0=(0,0,0),协方差阵Σ0的元素为0.5|i−j|,i,j=1,2,3)和xi∼N(0,0.25),i=4,5,···,10.其它假定均和第一个模拟研究中的一致.

同理用上述设置产生的两组模拟数据集在模拟一中考虑的三种先验情形下分别进行模型参数估计,为了节约空间,只列出无先验信息情形下参数的RB计算结果.具体为:

假定(1)中回归参数向量β的RB计算值分别为:

0.0008,−0.0087,0.0182,−0.0267,−0.0355,0.0186,−0.0216,−0.0078,−0.0418,−0.0434,

幂指标参数p的RB计算值为:0.0080,散度参数φ的RB计算值为−0.1445;

假定(2)中β的RB计算值为:

−0.0404,0.0117,−0.0231,−0.0221,−0.0167,−0.0016,0.0374,−0.0137,−0.0177,−0.0186,

幂指标参数p的RB计算值为:−0.0157,散度参数φ的RB计算值为−0.4314.

从上述计算结果发现,在模拟设置中,随着协变量多重共线性的严重程度增加时,模型的散度参数φ的估计偏差增大,而对参数向量β和幂指标参数p的估计影响较小.

在第三个模拟研究中,假定模型的系统部分表为:

log(µi)=β0+β1xi,

其中样本量m=150,协变量xi来自于均匀分布U(−1,1),回归参数向量β、散度参数φ、指标参数p的真值分别为:βT=(β0,β1)=(0.5,0.5)、φ=2、p=1.6.基于上述模型在模拟数据集中通过如下两种情形分别产生异常点.

情形一,把协变量重置为:

x1=x1+8,x75=x75+8,x150=x150+7;

情形二,把响应变量重置为

yi=yi+10,i=1,75,150.

并基于上述的混合算法产生的参数迭代值计算两类Bayes数据删除影响测度Dφ(i)和CM(i),只列出情形二下这两类影响测度的散点图(见图2).从图2可看出,正如所预期的一样,数据点1,75,150被识别为异常点.

图2 模拟研究中两类Bayes数据删除影响测度Dφ(i)和CM(i)的散点图

§6 实例分析

在这个部分里,分析的一组包含240份汽车保单的索赔数据来自Ismail[21],该数据集包括车年数,索赔次数,索赔强度,其中索赔强度等于平均每次索赔的赔款金额.模型的响应变量是累计损失,表示在保险期间累计的索赔金额,其数值等于索赔强度与索赔次数的乘积.另外,数据集包括5个因子解释变量及其对应的水平:保单类型(综合险,非综合险),汽车产地(国产,进口),汽车用途和驾驶人性别(商业,私人-女性,私人-男性),车龄和行驶区域(0-1年,2-3年,4-5年,6年以上),行驶区域(中部,东部,东马来西亚,北部,南部).在数据预处理过程中,发现有7份保单中车年数均为0,因此只分析其它233份保单的数据.对响应变量做变换,令y=y/100000,变换后的数据样本均值为1.7029,样本方差为19.154,零数据的比例为56.7%.这里,用上述发展的Tweedie回归模型对该数据集建立模型,其模型系统部分表示为:

log(µi)=log(di)+β0+β1xi1+β2xi2+ ···+β11xi,11,

其中车年数的对数log(di)是抵消项,虚拟变量x1,x2,x3,x4,x5,x6,x7,x8,x9,x10和x11分别表示非综合险水平,进口水平,私人-女性水平,私人-男性水平,2-3年水平,4-5年水平,6年以上水平,东部水平,东马来西亚水平,北部水平,南部水平;而把综合险水平,国产水平,商业水平,0-1年水平,中部水平分别作为各个分类变量的基准水平.在利用前面提出的Bayes混合算法对参数进行估计时,由于不知道未知参数的真实值,因此采用回归参数的无先验信息,即令

β0T=(0,···,0)12×1,

协方差阵

Σ0=100I12.

为了检验算法的收敛性,用模拟研究中所引进的方法来计算14个参数的EPSR值,其计算结果见图1(右图).从该图可以看出,当迭代次数约为500次时,所对应的14个参数的EPSR值均小于1.2,说明所使用的混合算法在500次左右时就已收敛.因此,在进行Bayes估计时,丢掉前面5000次迭代值而保留后面5000次迭代值用来进行计算.通过计算得到散度参数φ的估计值(标准差)为0.6381(0.0431),幂指标参数的估计值(标准差)为1.4193(0.0217);另外模型回归参数的估计值(标准差)分别为-12.3324(1.1789),-0.5805(0.1947),0.0092(0.1294),6.6860(1.1684),7.3796(1.1651),-0.5943(0.1639),-0.9383(0.1685),-0.9665(0.1590),-0.6654(0.2168),-0.5250(0.2115),-0.2655(0.1490),-0.0662(0.1650).

类似于模拟研究,用上述的混合算法产生一系列随机样本,丢掉所有参数的前5000次迭代值并利用后5000次迭代值来计算Bayes数据删除影响测度Dφ(i)和CM(i)的值,然后作出它们的散点图,结果见图3.从图3可看出:数据点1和6被Dφ(i)和CM(i)测度同时诊断为异常点.