5×5棒束通道内流动转捩特性研究
2020-12-15郝思佳祁沛垚乔守旭谭思超王啸宇
郝思佳,李 兴,祁沛垚,乔守旭,谭思超,*,王啸宇
(1.哈尔滨工程大学 核安全与仿真技术国防重点学科实验室,黑龙江 哈尔滨 150001; 2.中国核动力研究设计院,四川 成都 610041)
棒束通道的流动传热特性在反应堆热工水力分析中占有重要地位,其内部复杂多变的湍流特性是堆芯热工水力研究的重点之一,其中流动转捩现象是研究湍流特性的重要环节。转捩点一般是指从层流转变到过渡流的临界雷诺数,Hawley等[1]和Cheng等[2]提出该点可通过沿程阻力系数的拐点判断。不同于光滑圆管层流与过渡区具有明显界限,棒束通道流体转捩点并不明显[2-3],因此有必要对这一现象产生的原因加以分析。
国内外学者对圆管、棒束通道、平板流动的转捩情况已展开研究。Ohmi等[4]总结了不同工况下圆管流体阻力特性的基本规律。Gundogdu等[5-6]针对圆管流动建立数学模型,分析了层流、过渡流以及湍流状态下圆管内部流动阻力的主要来源。张川[7]和Zhuang等[8]针对窄通道流动阻力特性开展了大量的实验研究。王嘉兴[9]利用直接数值模拟的方法计算了超声速来流条件下平板边界层的转捩。张永兴[10]对曲面边界层转捩过程开展了实验与数值模拟研究。陈灿平[11]提出了基于层流动能概念和k-ω湍流模型而发展的一种新型模型预测转捩。目前对于棒束通道转捩情况的研究开展较少,相关研究主要是对棒束总体的沿程阻力特性进行分析[12-14],但并未具体分析棒束流体转捩点不明显这一现象产生的原因。
因此,本文拟对棒束通道内转捩点不明显的原因进行仿真研究,利用实验结果对仿真结果进行验证,并进一步研究不同子通道及子通道不同位置的速度、摩擦阻力、湍流强度等参数对流动转捩的影响。
1 几何模型与网格划分
1.1 几何模型
由于棒束通道几何结构的对称性,可认为同一水平截面的压力分布具有对称性,为提高计算效率,选取右下方1/4截面部分建模。几何模型与实验本体截面参数保持一致。图1为棒束通道几何模型与数值模拟选取的监测点位置及坐标系。
选取4根棒周向不同角度位置以研究棒束通道不同棒束不同位置的转捩规律。监测点成对存在,分别位于上下两个监测平面上,两平面间距为0.15 m。如图1所示,棒A每隔15°选取1个监测点;棒B、C、D隔45°或135°选取监测点。选取的监测点分两类:一类为位于距棒圆心5.25 mm圆周上的红色点;一类为位于相同角度棒A壁面处的蓝色点。同时,为研究不同子通道的阻力特性,选取图1所示4个子通道进行分析。
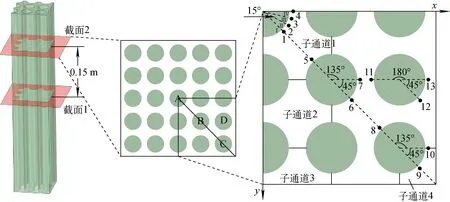
图1 几何模型与监测位置Fig.1 Geometric model and measurement position
1.2 网格划分
仿真采用非结构化网格进行网格划分。对于近壁面流动计算,壁面网格的划分较为重要,不同壁面处理方式对壁面网格划分要求不同。本文采用平滑过渡,控制壁面处y+值小于5(即第1层网格质心到壁面的无量纲距离)。通过调节单元格尺寸以及附面层数建立了4种网格模型,网格主要参数设置列于表1。
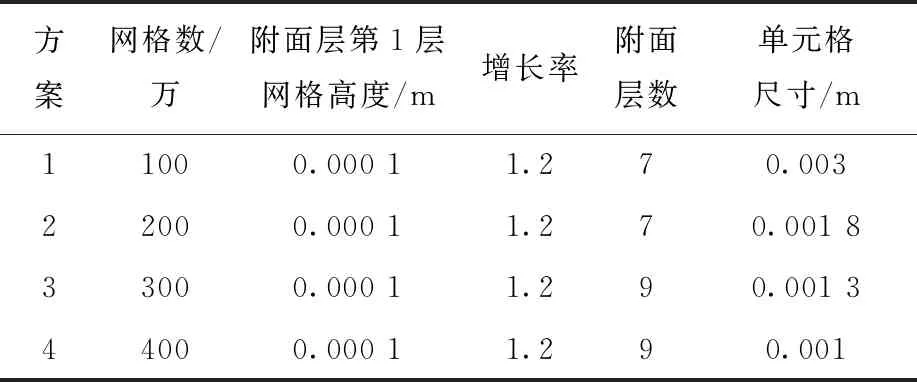
表1 主要网格参数Table 1 Parameter of main grid
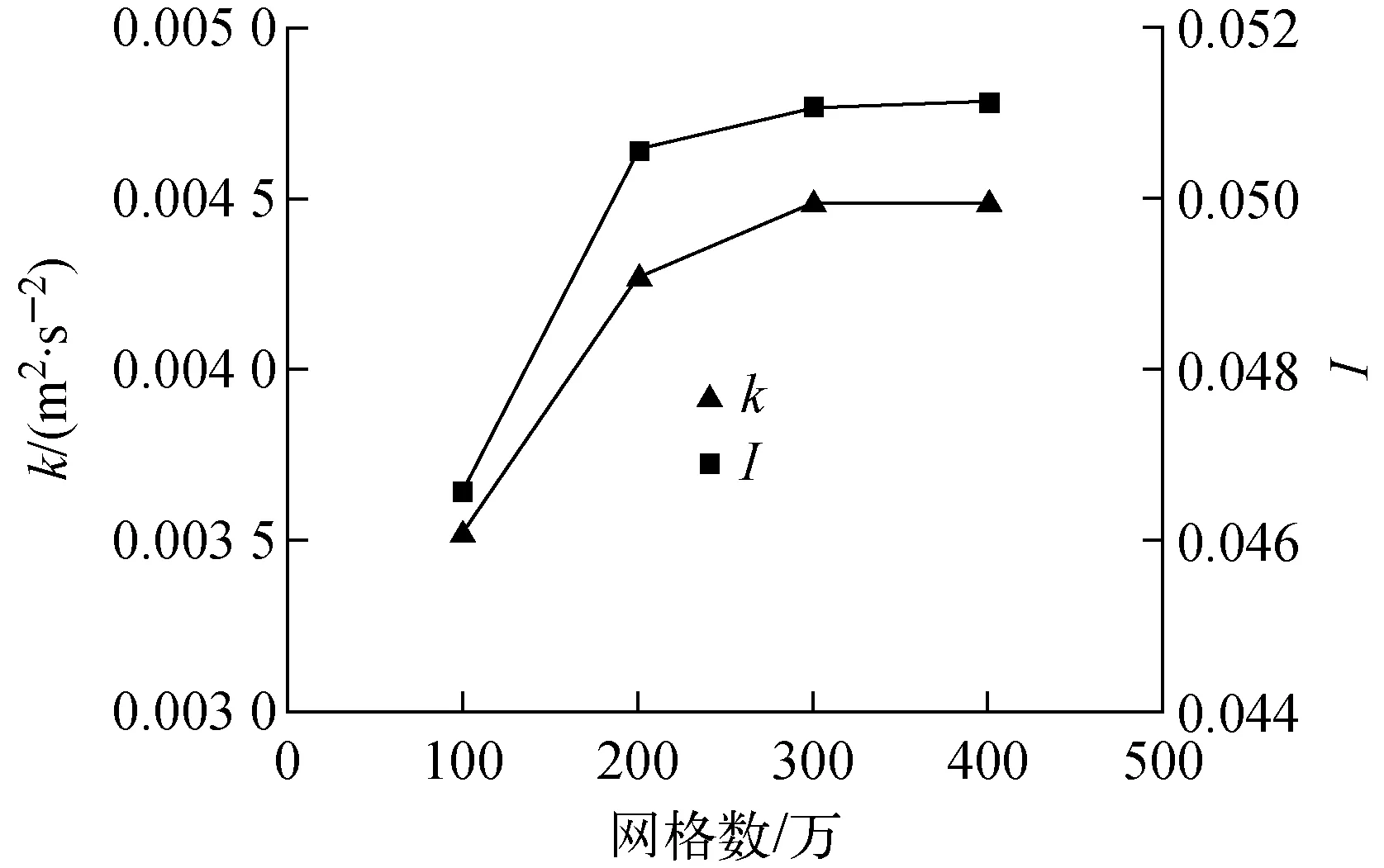
图2 网格敏感性分析Fig.2 Sensitivity analysis of grid
选取截面2的湍动能k与湍流强度I,采用SSTk-ω模型对4种网格模型进行敏感性分析,结果示于图2。可看出,随着网格数量的增加,4种方案的计算结果逐渐收敛,方案3与方案4的最大相对偏差低于0.4%,可认为方案3满足网格无关性,因此本文选取的网格数量为300万。
2 分析方法与实验验证
2.1 数据处理方法
本文主要对子通道阻力系数及湍流强度等特性进行分析。其中棒束通道内压降Δp由重位压降Δpg、加速压降Δpa、摩擦压降Δpf、局部压降Δpp组成(式(1))。重位压降是由于重力势能的变化而引入的压降,由式(2)计算。由于流动截面不变,没有加速度,因此无加速压降与局部压降。摩擦压降定义如式(3)所示,由此可根据式(4)计算沿程阻力系数。
Δp=Δpg+Δpa+Δpf+Δpp
(1)
Δpg=gρ(z2-z1)
(2)
(3)
(4)
式中:g为重力加速度;ρ为流体密度;z1和z2分别为截面1和2的高度;λ为沿程阻力系数,对于特定几何结构,沿程阻力系数与雷诺数有关,可通过实验或数值模拟获得不同雷诺数对应的沿程阻力系数;L为流道长度;V为流体入口流速;Dh为水力直径;A为流道横截面积;P为湿周。
湍流强度I与湍动能k均为衡量转捩的重要条件。湍流强度I定义为脉动速度均方根与平均速度的比值,如式(5)所示。湍动能k体现为速度与湍流强度的耦合作用,计算公式如式(6)所示。
(5)
(6)
2.2 实验
实验在棒束通道PIV流动平台上进行。实验系统由数据测控系统和实验回路组成,如图3所示。实验工质为常温去离子水,在变频器的控制下,实验工质经过水泵流入实验本体后返回水箱,完成1个循环。在实验本体外壁设置2个垂直距离15 cm的取压孔以测量上、下游压强,压降采用压差变送器(量程为2 kPa,精度为0.1%)测量。实验本体为5×5棒束通道,棒直径为9.5 mm,棒间距为12.6 mm,流道尺寸为64.1 mm×64.1 mm,流道的水力直径约为9.752 mm。
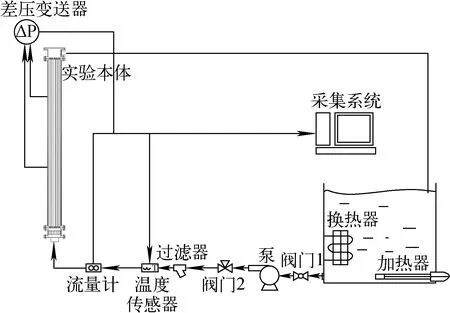
图3 棒束通道试验系统Fig.3 Rod bundle test facility
将实验测得的结果根据式(4)计算得出沿程阻力系数,并与仿真结果进行对比,以验证仿真结果的准确性。
2.3 充分发展段验证
为验证所选区域已达到充分发展,对入口下游不同位置静压与速度进行了纵向对比,结果如图4所示。可见,入口效应对静压的影响范围较小,同一入口雷诺数下静压随距入口长度的增大而线性减小,这体现了沿程摩擦阻力的影响。由速度分布可见,流体在入口下游约0.25 m(约25Dh)处达充分发展,因此本文选取距入口0.25~0.4 m范围的压降计算沿程阻力,此段不受入口效应影响。
为比较不同高度边界层发展,对不同高度子通道间隙流速进行对比。图5为子通道1棒间隙处速度分布,横、纵坐标均已无量纲化。图中边界层厚度从0.2 m以后已基本一致,可认为处于充分发展阶段,本文所选取的分析区域均在0.2 m以后。
2.4 计算模型验证
本文选择工程计算中常用的湍流模型沿程阻力计算结果与实验结果和Blasius经验公式进行比较,分别是标准k-ε模型、RNGk-ε模型、k-ω模型、SSTk-ω模型,结果示于图6。流体温度为常温,入口边界采用均匀流速入口,出口边界为压力出口,棒束、本体表面均设置为无滑移壁面。

图4 不同高度处流体参数Fig.4 Fluid parameters at different heights
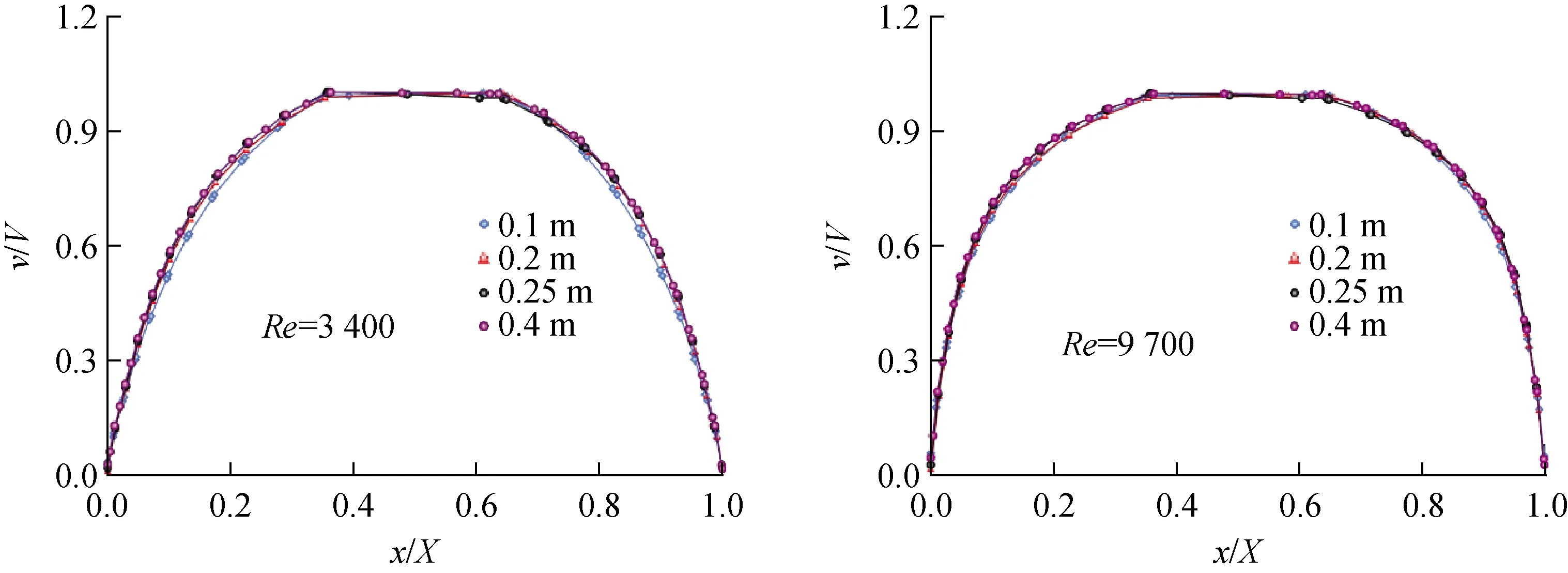
图5 子通道1不同高度处无量纲速度分布Fig.5 Dimensionless velocity distribution at different heights of subchannel 1

图6 计算模型与实验结果对比Fig.6 Comparison between CFD simulation and experimental results
由图6可看出,棒束内沿程阻力系数与圆管有很大不同,摩擦阻力曲线有一较大的过渡区。由于棒束结构的特殊性,复杂的壁面结构会对阻力系数产生影响,因此二者数值上也会有一定差距,但总体上随雷诺数的增加二者差距趋于减小。
经计算发现,k-ω系列模型计算准确度优于k-ε模型,这可能是由于k-ω系列模型对近壁面湍流模拟较准确。其中,SSTk-ω模型的计算结果与实验结果最为贴合,一些学者也提出过这一观点[15]。且SSTk-ω模型本身即是用于模拟湍流转捩过程的四方程转捩模型。因此本文选取SSTk-ω模型进行棒束通道转捩计算。
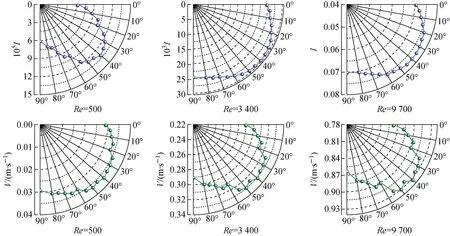
图7为棒A周向不同角度不同计算模型对湍流强度的计算结果。由图7a可见,不同湍流模型对湍流强度的敏感性较大。取相同位置处I/I均(I均为所选区域平均湍流强度)进行分析,结果如图7b所示。不同模型主要影响湍流强度大小而不影响分布趋势,即同一工况下不同模型的计算结果基本一致。综合以上考虑,选取SSTk-ω模型进行计算。
3 结果与分析
3.1 速度分析
转捩等湍流特性与雷诺数紧密相关,在其余条件一定时,速度的大小决定雷诺数的大小,因此要在研究速度分布的基础上对湍流特性展开研究。
图8为子通道不同位置处流体轴向速度云图与速度分布。其中L1、L2、L4分别位于两个中心子通道与边角子通道正中心位置,L3、L5分别位于边角子通道间隙的边角位置,具体位置如图8所示。可看出,不同中心子通道的速度大小与分布趋势相似,这是由于中心子通道的结构都是相同的,因此会有相似的速度分布以及速度值。对于边角子通道,由于本体壁面的影响,此类通道与中心通道速度分布会有较大区别。
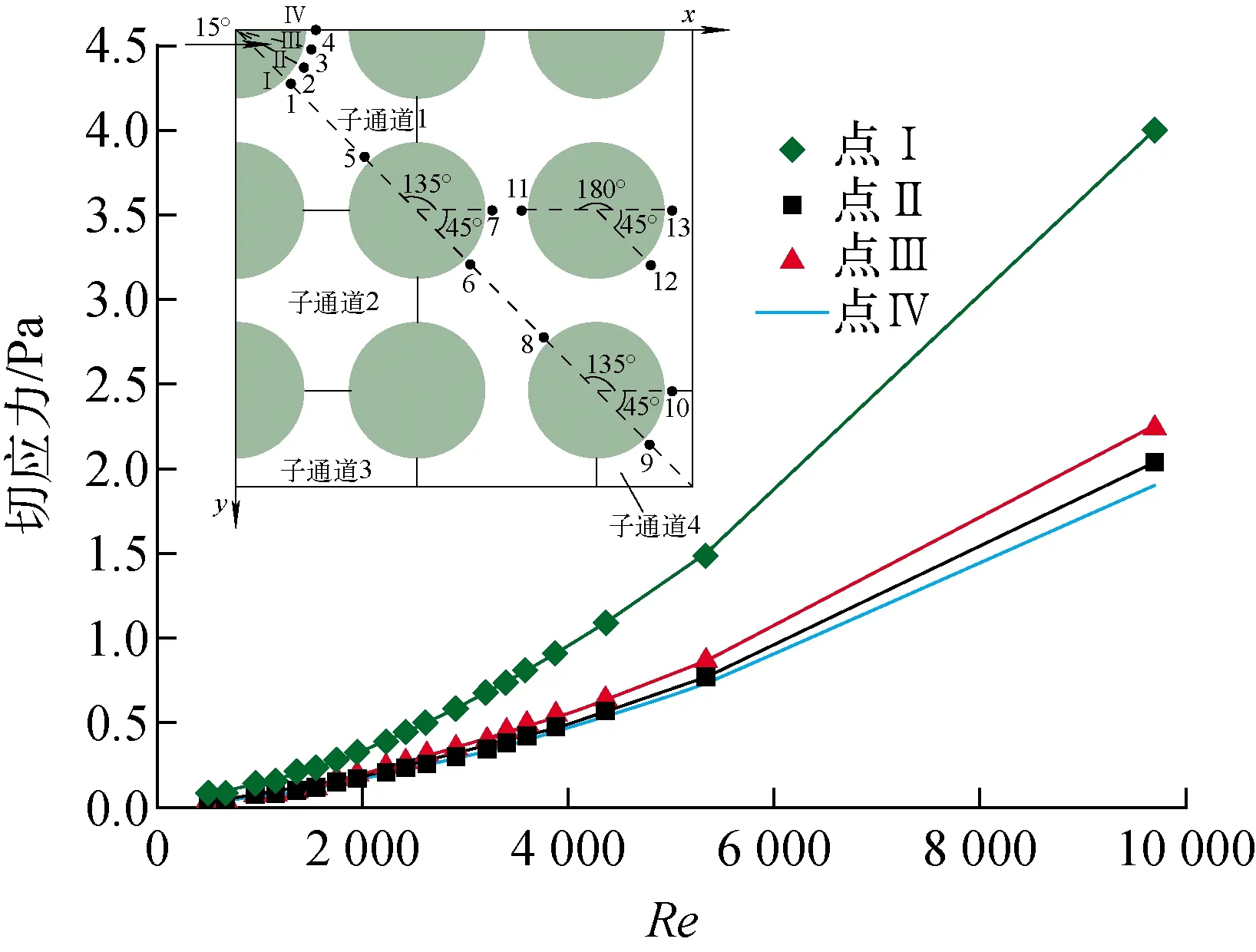
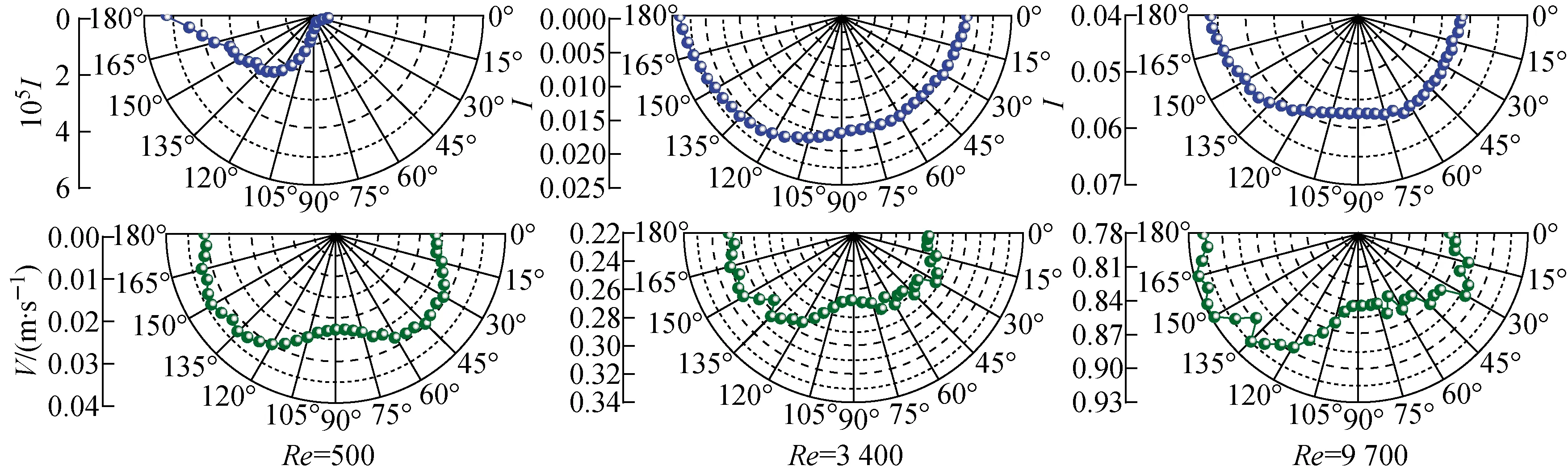
相比于圆管所有壁面到圆管中心线的距离相同,棒束通道内不同子通道的结构均不具备类似于圆管的高度对称性。图9a为圆管与不同子通道的结构,壁面处均用红线标记,黑色虚线处的流体与周围子通道流体相连。对于中心子通道,周围有4根棒存在,会同时受到4根棒的圆弧状边界层影响;同理,边子通道会受到2根棒与壁面边界层的影响;角子通道会受到1根棒与2个壁面的影响。图9b为边界层对速度分布的影响。设棒壁面边界层厚度与棒半径之和为R1、通道壁面边界层厚度为R2、相邻棒间距为S1、对角线棒间距为S2、棒中心与通道壁面距离为S3、棒中心与壁面角距离为S4。棒束中心子通道内流体流动理论上会出现如下3种情况:2R1>S2;S1<2R1 图7 不同模型棒A周向湍流强度对比Fig.7 Comparison of turbulence intensity around rod A under different models 图8 流体速度分布Fig.8 Fluid velocity distribution a——不同子通道结构对比;b——边界层对速度分布的影响图9 不同子通道结构对流动的影响Fig.9 Effects of different subchannel structures on flow 随着雷诺数的增加,边界层厚度会不断变薄,从层流到湍流会依次经历上述3种情况,第1种情况一般不会在节距比较大的传统棒束中出现。边界层厚度的变化会导致中心子通道不同位置流体速度分布具有较大差异。 随着雷诺数的增加,边界层厚度会不断变薄,从层流到湍流会依次经历上述3种情况,但第1种情况一般不会在S4较大的传统棒束中出现。因此边角子通道内流体所处空间位置不同,主要受到的壁面影响来源不同,也会造成速度分布不均。 通过对速度的分析,可看出棒束通道内处于不同位置的流体速度,会受到通道壁面或棒壁面边界层的耦合影响,而速度特性与转捩等湍流特性密切相关,可认为两种壁面边界层的耦合影响是导致棒束流体过渡区难以分辨的原因之一。 从3.1节可知,壁面效应会造成不同子通道速度特性产生差异,该差异可能会对子通道间阻力特性产生影响,因此本节对子通道间阻力特性进行分析,该阻力特性已不含入口效应。 假设子通道间横向流动忽略不计,在这一假设条件下,对不同子通道沿程阻力系数进行分析。为证明假设的合理性,定义了流道长度内流体横向移动的最大距离s与无量纲横向移动距离ω,计算公式如(7)、(8)所示。经计算发现,所选取工况中ω均小于0.1%,可认为通道间横向流动忽略不计,子通道均为独立个体。 s=L/v×umax (7) ω=s/S (8) 图10 不同子通道的沿程阻力系数影响Fig.10 Influence of different subchannels on resistance coefficient 由3.1节可知,不同子通道壁面结构对子通道内部流体的耦合影响不同,可能会导致不同类型子通道的阻力特性各异,因此对不同子通道沿程阻力进行分析。图10为不同子通道沿程阻力系数随雷诺数的变化。图中,子通道1、2为不同位置的中心子通道;子通道3为边子通道;子通道4为角子通道。雷诺数为子通道的雷诺数,压降选取为该子通道截面1、2间压降。通过对比子通道阻力系数曲线,中心子通道的转捩雷诺数可通过沿程阻力系数曲线明显分辨出,此处流体转捩较强,而边角子通道的转捩过程受壁面抑制效果更强,导致此处转捩前后曲线斜率变化不大,转捩的影响较弱。3类子通道对应的转捩雷诺数虽不同,从中心子通道到边角子通道递减,但由于流速分布也是中心子通道到边角子通道递减,对于同一入口雷诺数,不同子通道转捩点相差不大,只是转捩对不同子通道流动情况的影响程度不同,因此3类子通道之间的影响互相中和,共同促使了整个棒束通道从层流进入过渡区的转捩点不如圆管转捩点明显。 为进一步研究棒周向不同位置转捩特性,选取棒壁面点Ⅰ、点Ⅱ、点Ⅲ、点Ⅳ的壁面摩擦阻力进行分析。图11示出棒A不同周向角度处壁面切应力的变化。点Ⅰ处壁面切应力大小明显高于其余3点,此现象与Bae等[16]的结论相同。在点Ⅰ附近流场区域会受到较大切应力的影响,即此处有更大的速度梯度并带来更多扰动,使得此位置附近流体的湍流扰动高于点Ⅳ附近,导致沿棒周向流体湍流发展的程度各异。 图11 周向位置壁面切应力分布Fig.11 Circumferential position wall shear stress distribution 综上分析,转捩现象在不同类型子通道对流态的影响强弱不同,中心通道受到的影响更强;对于同一子通道周向位置,子通道中心附近棒壁面切应力更大,会对此处流体带来更多扰动,造成棒周向流体湍流发展程度不均匀。这种不均匀性会导致棒束内流动转捩点不明显。 根据Bae等[16]的研究,棒束通道内部存在阻力分区的现象,即沿同一根棒的周向不同角度会存在不同的壁面切应力,靠近子通道边缘处棒壁面切应力最低,子通道中心处棒壁面切应力最高。可推知湍流强度的分布亦会出现沿棒周向分区的现象,因此本节针对不同空间位置流体湍流强度特性进行分析。 围绕棒A周向距棒壁面0.5 mm处取点,其周向湍流强度与速度分布示于图12。速度与湍流强度沿周向分布具有相似性:子通道边缘处(0°或90°)由于流通面积小和受到壁面影响更大的双重作用,导致速度与湍流强度低于子通道中心处(45°)相应参数。这说明沿棒周向子通道中心附近的湍流强度高于同一工况下子通道边缘湍流强度,湍流强度表征了流体微团的脉动程度,湍流强度越高,流体越趋向于湍流。这种棒周向湍流强度不均匀性会影响棒束内部整体的转捩情况。 围绕棒C周向距棒壁面0.5 mm处取点,其周向湍流强度与速度分布示于图13,图中0°~90°位于角子通道,90°~180°位于边子通道。当雷诺数较低时,角子通道的湍流强度远低于边子通道,这是基于两道通道壁面与棒壁面共同抑制作用的结果,当流动逐渐发展为湍流时,角子通道的湍流强度将明显增加并逐渐接近于边子通道湍流强度,但在所研究雷诺数范围内,边子通道湍流强度均大于角子通道湍流强度。这说明了不同类型子通道之间湍流强度的不均匀性,子通道间湍流强度不均匀性相互作用也是棒束内流体整体上转捩点不如圆管明显的原因之一。 综上分析,由于壁面抑制作用导致的棒束通道流体湍流强度不均匀性是棒束转捩点不明显的原因之一,该不均匀性总体上会呈现:中心子通道流体湍流强度高于边子通道湍流强度高于角子通道湍流强度;靠近子通道中心处流体湍流强度高于靠近子通道边缘处流体湍流强度。 图12 棒A周向湍流强度与速度分布Fig.12 Distribution of turbulence intensity and velocity in rod A circumferential direction 图13 棒C周向湍流强度与速度分布Fig.13 Distribution of turbulence intensity and velocity in rod C circumferential direction 本文采用实验与CFD数值模拟的方法对5×5棒束通道内的流动转捩特性进行了研究,获得了棒束通道不同子通道及同一子通道不同位置湍流强度与沿程阻力系数等参数的变化规律,得到以下结论。 1) 由于棒束通道壁面结构复杂,壁面效应的互相影响会使得不同子通道以及子通道不同位置的速度等流动特性分布不均。 2) 由于壁面对流体的抑制作用,棒束通道内部转捩不是同时发生的,具体表现为:从子通道中心转捩发展到棒壁面附近转捩;不同类型子通道流体受转捩影响的程度也有所不同。转捩发展的不同步性,会引起棒束通道流动的转捩点不明显。 3) 棒束通道内湍流强度不均匀,总体上会呈现:中心子通道流体湍流强度高于边子通道湍流强度高于角子通道湍流强度;靠近子通道中心处流体湍流强度高于靠近子通道边缘处流体湍流强度。这一不均匀性也会使得棒束通道转捩点不明显。


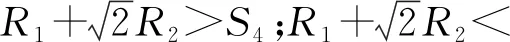
3.2 阻力特性分析

3.3 湍流强度分析
4 结论
