基于改进NARX-DMC的SCR脱硝控制策略

邢波涛， 乔 源， 赵文杰

(华北电力大学 控制与计算机工程学院，河北 保定 071003)

收稿日期：2020-05-04.

基金项目：国家重点研发计划项目(2016YFB0600701).

0 引 言

近年来由于电网频繁调峰对燃煤电厂锅炉燃烧系统的冲击，使得燃煤电厂锅炉烟气中氮氧化物(NOx)浓度的波动十分剧烈，而由于SCR脱硝系统大时延、多扰动、强非线性的特点，以及烟气测点的不准确性、测量装置吹扫等多个因素，SCR脱硝系统进行优化控制的策略研究一直以来都是一个难点，现在大多数燃煤电厂中采取以下方法：其一，人工手动控制，运行人员利用经验观察机组负荷等变量变化，对SCR脱硝系统出口NOx排放值进行手动控制调节，控制品质较差；其二，固定摩尔比的控制，这种控制方法是利用SCR入口NOx浓度，计算对应反应的NH3量，然后作为PID控制器前馈[1，2]，但是由于测量滞后，这种方法并没有取得理想的控制效果。为此设计一种先进有效的控制策略就显得尤为重要。孙育红等人[3]通过非线性拟合方法建立了SCR烟气脱硝系统入口NOx质量浓度预测模型，同时在对现场数据进行辨识的基础上，设计了针对迟延环节的Smith预估模型控制器,优化了控制性能；任志玲等人[4]建立选择性催化还原系统出口NOx的径向基函数神经网络预测模型，采用混沌局部搜索算法确定最大迭代步数，并利用混沌粒子群优化算法(CPSO)求取最优喷氨量，控制性能良好，但算法的时间复杂度和空间复杂度都过高，运算量较大，不适合实际现场应用。

本文采用电厂实际运行数据，建立SCR脱硝机理模型，提出一种NARX神经网络和改进DMC预测控制算法相结合的脱硝控制策略，实现对脱硝系统的优化控制。

1 SCR脱硝系统的机理建模

1.1 SCR反应原理

SCR脱硝系统反应器工作在烟气温度为300～400 ℃的反应环境下，选用NH3作为脱硝反应过程的还原剂，为使得选择性催化还原反应可以在烟气温度下进行，工程中通常使用催化剂V2O5/TiO2降低反应的活化能，并抑制副反应的发生，把锅炉烟气中的NOx，进行无害化技术处理，主要化学方程式如下所示[5]:

4NH3+4NO+O2→4N2+6H2O

(1)

4NH3+6NO→5N2+6H2O

(2)

烟气SCR脱硝反应原理见图1所示。

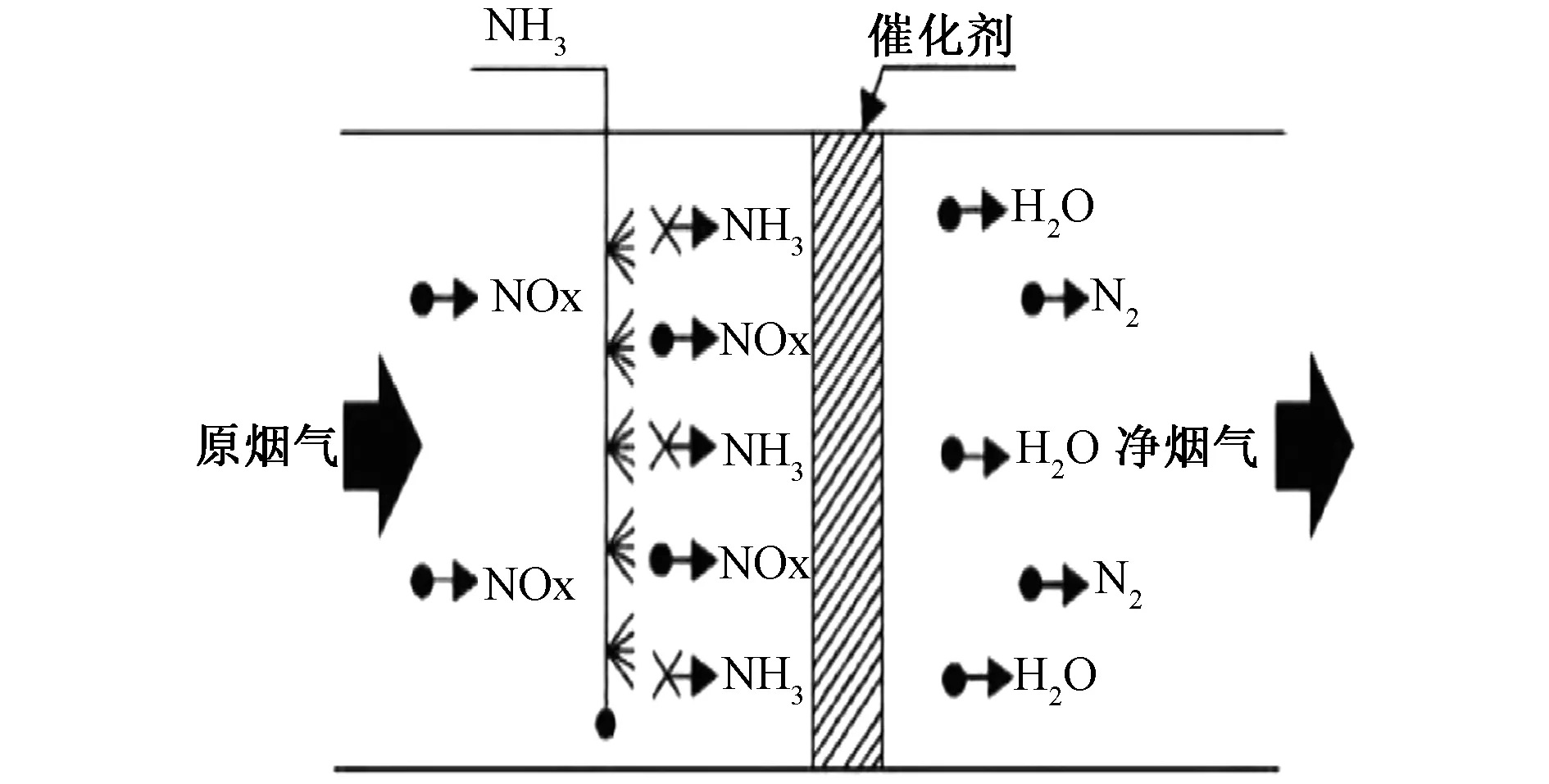
图1 SCR反应原理Fig.1 SCR reaction principle

脱硝反应的过程遵循如下两个动力学反应定理：Langmuir-Hinshelwood机理和Eley-Rideal机理。根据Langmuir等温吸附平衡方程，NH3在脱硝反应中的反应过程可以描述为以下几个过程：

(3)

(4)

(5)

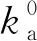
根据Eley-Rideal反应原理，NH3与NOx的反应过程可描述为[6,7]

(6)

(7)

(8)

(9)

rox=koxθNH3

(10)

(11)

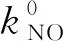
1.2 SCR机理模型参数辨识

采用从某电厂DCS获取的脱硝历史数据，以模型的输出与实际出口NOx浓度之间的最小误差为目标，用粒子群算法对上述公式中SCR脱硝系统机理模型的参数进行寻优辨识，辨识结果如表1。

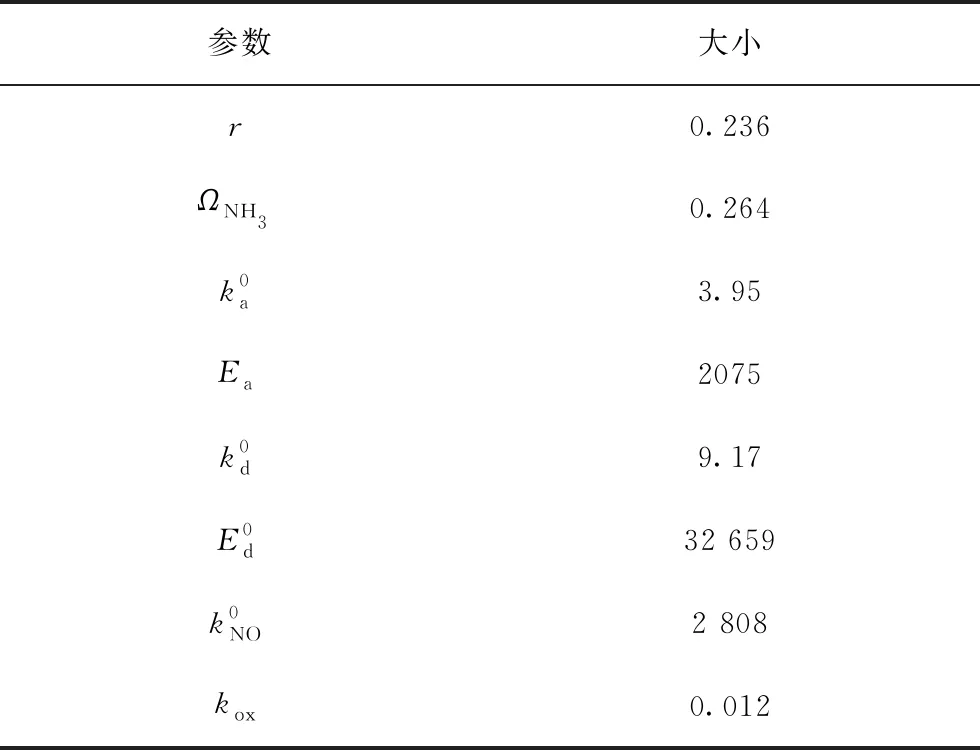
表1 脱硝机理模型参数

为测试机理模型的有效性，选取一段典型的实际数据，进行机理模型测试。将实际入口NOx浓度、喷氨量、总风量、SCR入口温度数据作为机理模型的输入数据，获得的机理模型输出与实际出口NOx浓度曲线如图2所示,模型输出与实际输出之间的均方根误差为4.35，因此经过辨识得到的SCR脱硝机理模型具有较高的准确性。

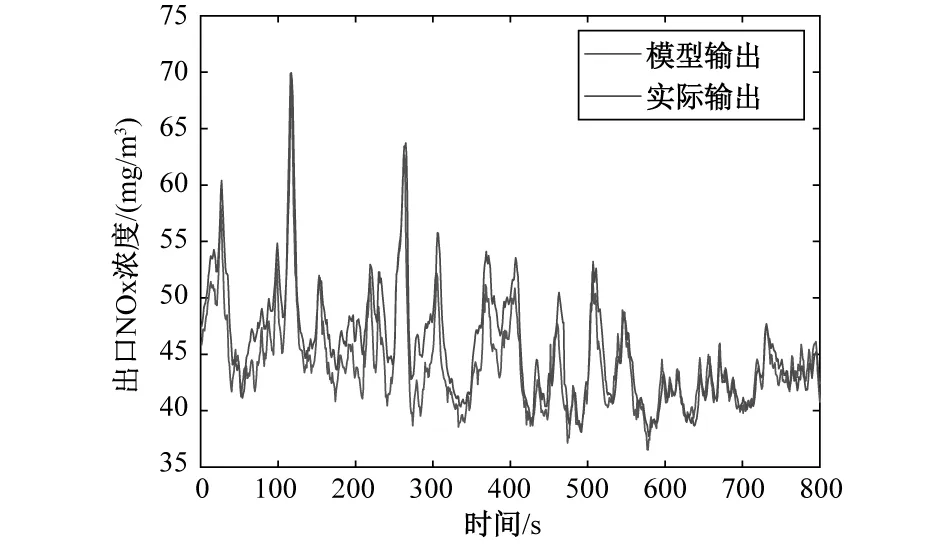
图2 脱硝系统机理模型输出曲线Fig.2 Output curve of mechanism model of denitrification system

2 SCR脱硝系统动态矩阵控制及改进

选取在工程应用中容易获得的阶跃响应做为预测模型的动态矩阵控制算法是在流程工业过程中应用十分广泛的预测控制算法之一，该算法在控制量的求取上使用增量算法，能有效消除被控对象反应过程中的稳态误差，因此适用于有纯时延、大惯性的被控对象[8]。动态矩阵控制算法主要由预测模型，滚动优化和反馈校正三个部分构成，其结构如图3所示。

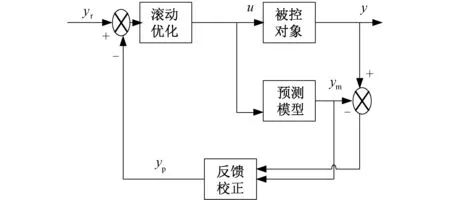
图3 动态矩阵控制的算法结构Fig.3 Algorithm structure of dynamic matrix control

2.1 预测模型

预测控制的核心思想是通过一个基本的预测模型去预估控制系统在未来时刻的输出，进而产生控制作用。因此，为了使预测控制策略实用化，间接地要求预测模型应该尽量准确，这样才能保证预测控制有良好的调节品质。传统动态矩阵控制算法选取了被控对象的单位阶跃响应数据序列作为控制算法的基本预测模型[9]，但考虑到现场脱硝系统本身所具有的非线性时变因素和各种复杂工况影响，本文采用NARX神经网络作为动态矩阵控制系统的预测模型。

NARX神经网络，是一种动态自回归神经网络，不同于BP神经网络输出与输入之间独立存在，它是神经网络的几个时间序列输出返回到输入端与新时间序列的输入共同构成神经网络的输入，从另一方面上说，NARX神经网络的结构就是具有多时间序列输入BP神经网络加入几个时间序列输出的反馈连接，因此NARX在非线性系统中有着非常突出的非线性映射能力及其在动态系统建模中展现的较好的动态特性[10]，适合实际的脱硝系统建模。

如图4所示，与一般BP神经网络相同NARX神经网络也是分为输入层、隐含层以及输出层三部分，这三层中分别包含i，j，m个神经元，每层神经元在传输过程中都会乘以一个权值系数然后再向下传递，然后与同层其他神经元的乘以权值之后的输出进行相加，最后经过一个非线性激励函数，形成对应下一层神经元的输入，对于激活函数可以对应不同需求有多种选择。

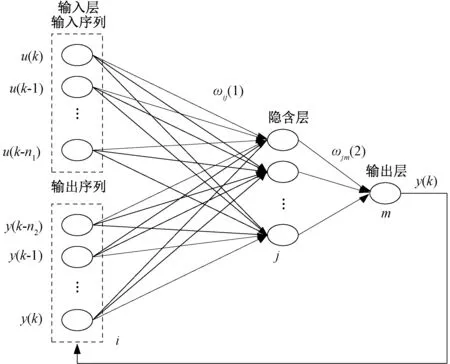
图4 NARX神经网络结构图Fig.4 Structure diagram of NARX neural network

在对被控对象神经网络建模过程中，一个多输入单输出系统的离散方程如式(12)所示。

y(k)=f[y(k-1),y(k-2),…,y(k-ny),

u1(k),u1(k-1),…,u1(k-n1),

u2(k),u2(k-1),…,u2(k-n2),…,

un(k),un(k-1),…,un(k-nn)]

(12)

式中：y(k)为被控系统的输出；u1(k),…，un(k)为被控系统的输入；ny为系统输出的时间序列延迟个数；n1,…,nn为系统输入的时间序列延迟个数。

对于SCR脱硝系统，研究中输入输出的阶次均选择为3阶，则得到如式(13)所示的神经网络模型结构。

yNOx(k)=f[yNOx(k-1),yNOx(k-2),

uNH3(k),uNH3(k-1),uNH3(k-2),

uNOx(k),uNOx(k-1),uNOx(k-2),

uwind(k),uwind(k-1),uwind(k-2),

utemp(k),utemp(k-1),utemp(k-2)]

(13)

式中：yNOx为SCR脱硝系统出口NOx浓度；uNOx为入口NOx浓度；uNH3为喷氨量；uwind为风量；utemp为烟气温度。

隐含层节点数设为10。隐含层激励函数选用双曲正切函数，如式(14)所示。

(14)

输出层激励函数选用双极性sigma函数，如式(15)所示。

(15)

SCR脱硝系统神经网络模型的结构如图5所示。

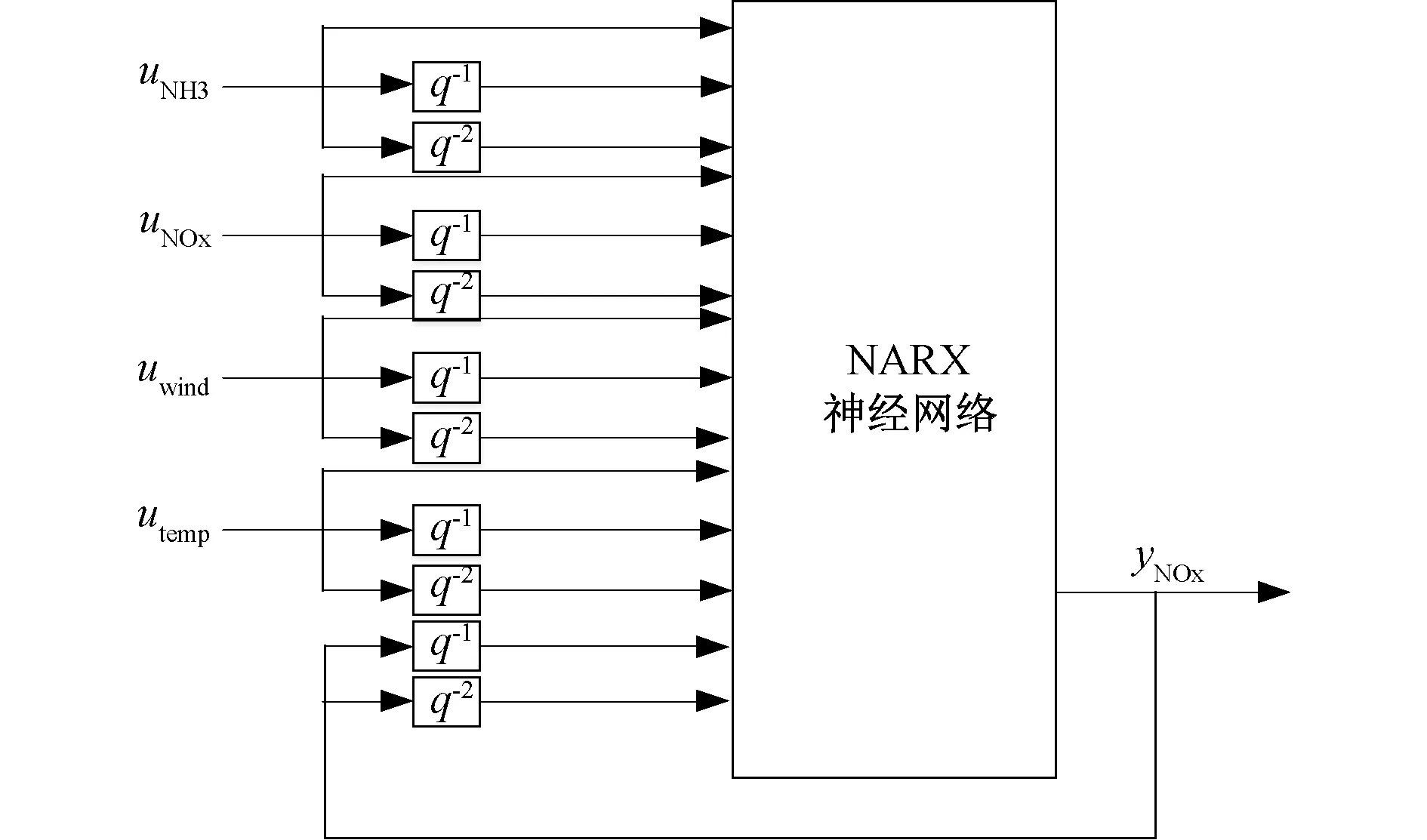
图5 SCR脱硝系统神经网络模型Fig.5 Neural network model of SCR denitrification system

选所取数据的前70%进行模型的训练，取后30%数据进行模型测试，得到预测模型的训练结果和测试结果分别如图6中(a)和(b)所示，模型的训练均方根误差和测试均方根误差分别为3.44和4.21，由模型的训练和测试曲线以及评价指标能够看出预测模型可以很好的预测出口NOx浓度的变化。

图6 SCR脱硝系统神经网络输出Fig.6 Neural network output of SCR denitrification system

2.2 滚动优化

传统动态矩阵控制算法将被控对象的单位阶跃响应序列作为基本的预测模型[11]，其预测模型为

YM=WMUM+Y0

(16)

其中：

UM=[u(k+M-1),…,u(k+1),u(k)]T

YM=[yM(k+1),yM(k+2),…,yM(k+P)]T

WM为预测输入时的模型，称为动态矩阵；{a1,a2,…,aN}为系统单位阶跃响应数据序列，UM为控制增量矩阵，Y0称为基本输出，即没有预测输入情况下的系统实测输出，P为优化时域，M为控制时域[12，13]。

式(16)表达的是如果给被控对象施加M个控制增量作用，那么根据系统可以进行比例和叠加的特性，就可以按该式得出被控对象在未来时刻对应的P个预测模型输出。也就是说，只要给出被控系统的未来P个时刻的输出设定值

Yr=[yr(k+1),yr(k+2),…,yr(k+P)]T

(17)

根据预测输出与设定输出最小化方差原则，就能计算出所需的未来M个控制量UM。

定义目标函数：

(18)

式中：hi,rj为加权系数。

令：

H=diag[h1,h2,…,hP]

(19)

R=diag[r1,r2,…,rM]

(20)

则可以把式(18)改写成矩阵的形式，即

(21)

把式(16)代入式(21)，然后根据极值必要条件，可以得到最优控制率为

(22)

从式(22)中可以看出，最优控制率的计算复杂程度主要与动态矩阵WM有关，也就是与P和M的大小有关，而在每一时刻求出的M个最优控制增量矩阵中,动态矩阵控制只是取其中的当前控制作用增量Δu(k|k)计算系统的实际控制率施加在被控对象上，并不是把滚动优化所得的所有最优控制增量都当作应实现的解，因此可通过引入一个衰减系数，将当前要实施的系统的控制量作为系统优化变量，未来其他时刻的系统控制量用当前控制量和衰减系数表示[14]，即

u(k+i|k)=ρiu(k|k)0<ρ<1

(23)

式中：ρ为衰减系数，集结矩阵为

将集结矩阵带入式(16)，在滚动优化时的计算量从原来需要求解M个控制增量简化为只需要求解Δu(k|k)即可，极大缩减了计算时间。

2.3 反馈校正

因为系统运行工况的复杂性和各种环境的影响，系统总会遭受各种扰动，这就会导致预测模型的输出与实际被控对象的输出存在相对的误差，要消除这种预测误差就要对齐进行反馈校正。当在kTs时刻采集到实际输出y(k)以后，把它与估计的预测输出yM(k+1)进行分析比较，得到预测误差为

e(k)=y(k)-yM(k+1)

(24)

再根据这个误差去修正各个预测输出值，即

yP(k+i)=yM(k+i)+cie(k)

(25)

式中：ci为加权修正系数，i=1,2,…,P。

但是这种误差校正方法只对根据当前的误差对预测模型输出进行反馈校正,而没有考虑到误差的变化情况,有可能会导致过渡时间偏长，误差干扰的校正不够迅速,没有很好的抗干扰能力。所以,在k时刻，可以根据当前已得到的误差e(k)和预测模型的预测输出误差e(k+1)计算得到误差变化率,引入到预测输出的反馈校正中，依据预测误差和误测变化趋势,迅速修正预测输出与实际输出之间的误差[15]。即

yP(k+i)=yM(k+i)+cie(k)+ge(k)

(26)

其中，

e(k)=e(k)-e(k+1),g=[g1,g2,…,gP],

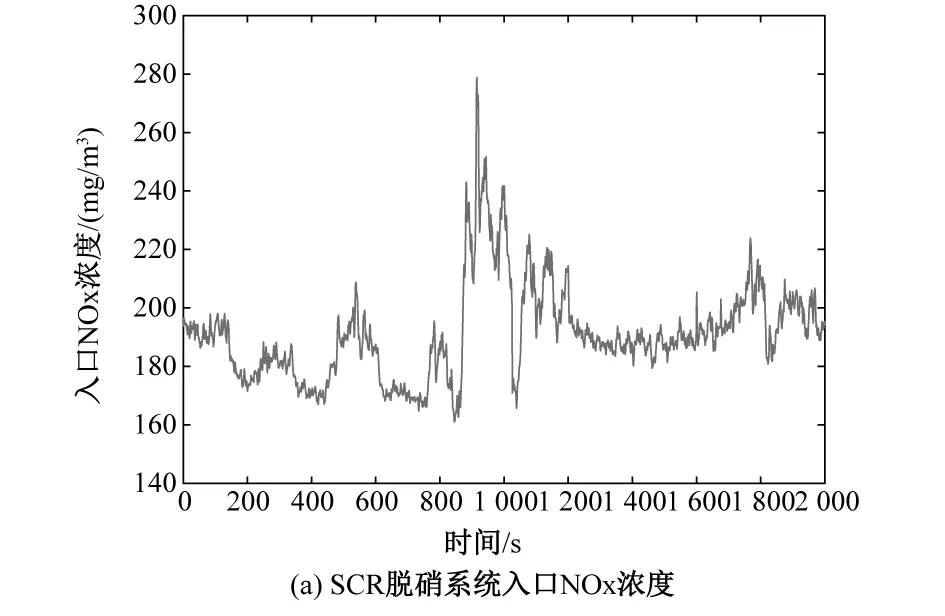
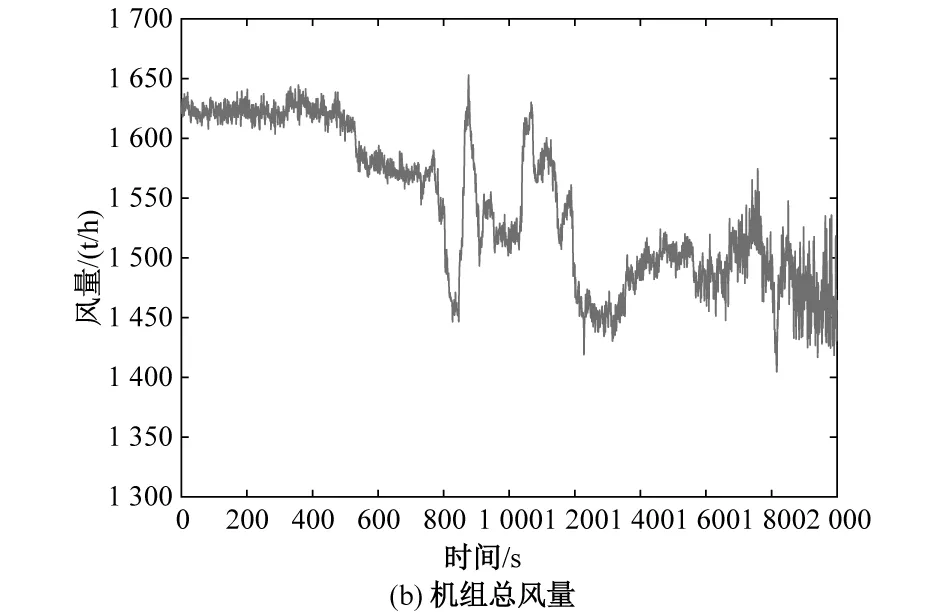
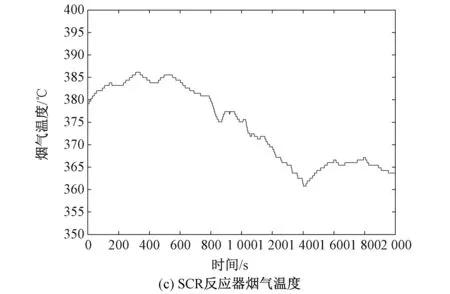
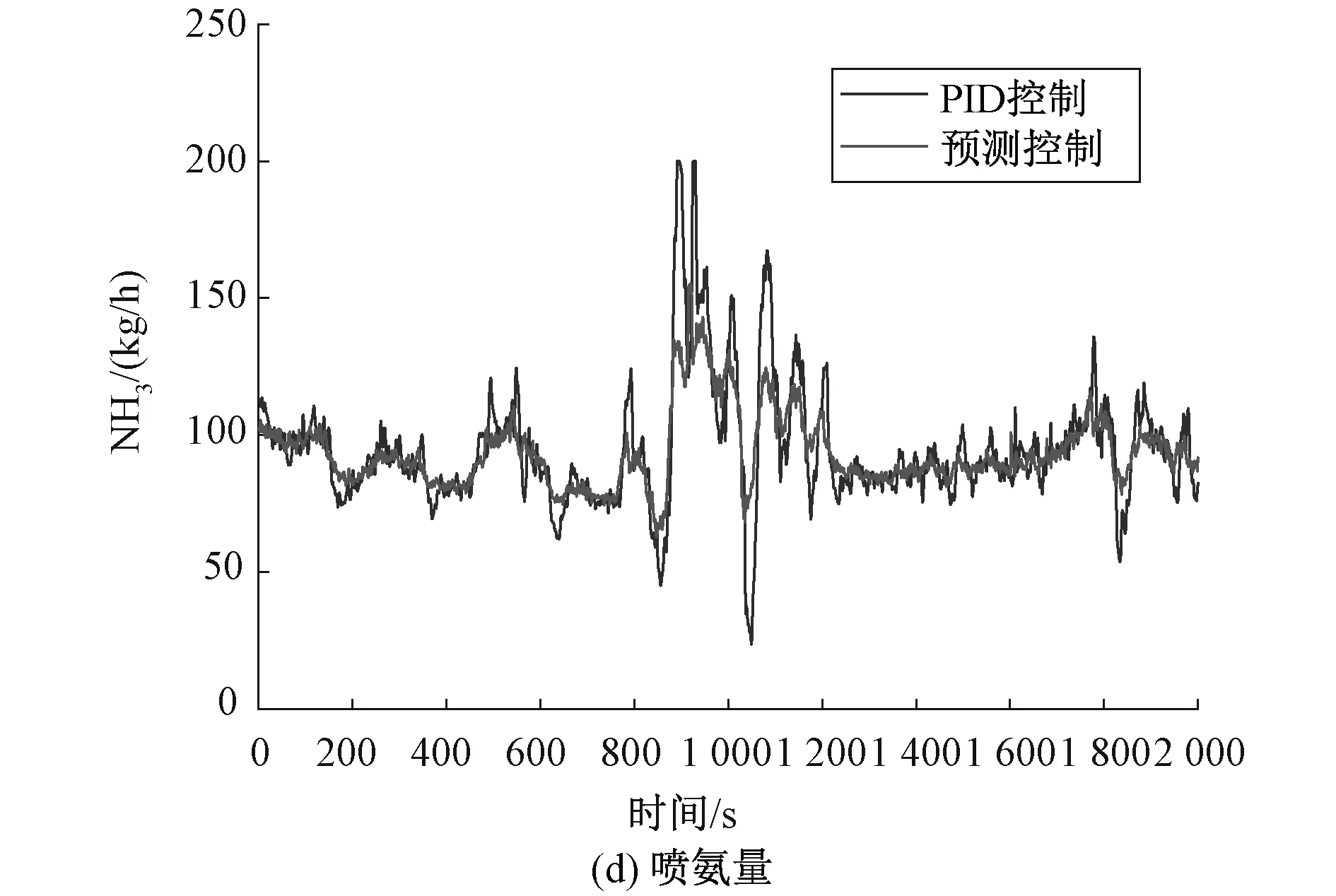
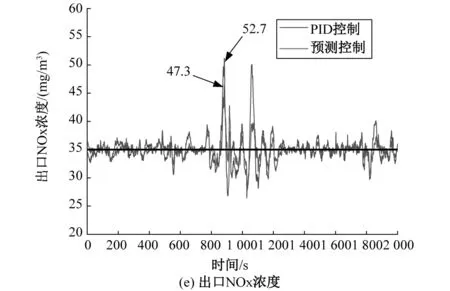
N,0

以第一小节得到的SCR机理模型作为被控对象，分别用传统的DMC算法和加入误差变化率的DMC算法进行MATLAB仿真试验,首先对得到的机理模型进行喷氨扰动实验，分析其动态特性，参数的大小要涵盖阶跃响应的主要动态部分，并结合控制效果选定DMC算法的优化时域P为30，控制时域M为5，出口NOx设定值设为35 mg/m3，在第100 s加入一个入口NOx阶跃信号，观察系统输出变化，从图7所示的仿真结果可以看出，当发生扰动时，加入误差变化率的DMC控制系统比传统DMC控制系统提前增大喷氨量，因此使得出口NOx浓度波动幅度相对较小，并且阀门动作幅度小，在获得更优的控制效果的同时一定程度的延长了执行机构的使用寿命。

3 仿真与分析

控制系统设计工作，最重要的步骤之一就是进行实际数据验证。本文为进一步验证NARX神经网络和改进DMC预测控制算法相结合的脱硝控制策略的有效性，在MATLAB中搭建仿真环境，出口NOx浓度设定值设置为35 mg/m3，使用从电厂采集的运行数据进行仿真分析验证，仿真结果如图8所示。

图8 DMC控制与实际系统比较Fig.8 Comparison between DMC control and actual system

从图8(e)可以看出，本文设计的预测控制系统的最大控制误差为12.3 mg/m3，即控制器最大输出为47.3 mg/m3，完全可以满足控制要求，在入口NOx剧烈波动的复杂工况下，控制效果也要明显优于原始电厂控制效果。而且本文设计的控制器的喷氨量波动较原始电厂控制器要小很多，这样可以有效延长喷氨执行机构的使用寿命。

4 结 论

针对SCR脱硝系统，本文提出了NARX神经网络和改进DMC预测控制算法相结合的控制策略，采用比阶跃响应序列更能拟合被控对象非线性特性的NARX神经网络作为预测模型，并在滚动优化时引入集结算法简化最优控制率的计算过程，以及在通过预测误差校正预测输出值的基础上加入预测误差的变化趋势，使得系统控制器能提前进行动作，消除外部扰动对被控对象的影响。通过仿真试验可以看出，基于NARX-MC的控制策略，具有良好的控制性能，能够为SCR脱硝控制系统的设计提供参考。