大型油浸式并联电抗器内外部振动测点数据相关性分析

郭佳熠， 王博闻， 律方成， 赵晓宇， 耿江海， 潘亦睿

(1.华北电力大学 河北省输变电设备安全防御重点实验室，河北 保定 071003； 2.华北电力大学 电气与电子工程学院，河北 保定 071003;3.中国电力科学研究院有限公司，北京 100192)

0 引 言

并联电抗器是高压远距离输变电系统中的重要设备之一，特高压并联电抗器是目前电压等级最高的一类并联电抗器，具有补偿长线路电容效应、限制工频电压升高、抑制操作过电压等多种功能[1]。自2006年至今，我国已有200余台特高压并联电抗器投入使用，在特高压交流输电工程中发挥了十分重要的作用。特高压并联电抗器的安全稳定运行是特高压交流输电线路可靠运行的关键。

与同电压等级的变压器相比，由于铁心包含气隙结构[2]，并联电抗器的振动特征更强，振动问题也因此成为并联电抗器研究的重点方向之一。在振动机制方面，河北工业大学闫荣格和华北电力大学李琳等团队提出了“电磁-机械”多场耦合模型，用于计算干式电抗器的振动参数[3-10]；华北电力大学律方成团队在其基础上考虑特高压并联电抗器铁心饼辐射结构和流-固耦合作用提出了计及铁心叠片规则与流-固耦合的特高压并联电抗器铁心振动计算方法[11,12]。在故障振动信号处理方面，河海大学马宏忠团队等提出了基于经验小波变换的振动信号分析方法，并通过机器学习等方法对并联电抗器的绕组和铁心松动故障进行的诊断[13,14]。从研究现状可以看出，电抗器的外部振动信号可以通过试验的方法直接测量，而电抗器内部的振动参数则仅可以通过理论计算的方法获得。并联电抗器内部的振动信号包含大量设备运行状态信息，准确获取这些信息对开展并联电抗器的在线监测和故障诊断至关重要。

对于特高压并联电抗器而言，绕组振动强度仅为铁心的约10%[15]，电抗器本体振动更多的是由于铁心振动引起的。并联电抗器铁心产生的振动可以通过液体(变压器油)和固体(紧固件和垫脚等)等路径传播到油箱并引起油箱的振动[16]。油箱不同位置的振动信号中包含的铁心振动信息也不尽相同。因此，有必要开展特高压并联电抗器铁心与油箱外壁振动信号的相关性研究，以期从油箱外壁诸多的振动点中选择包含较多铁心振动信息的测点用于后续振动的测量。从而实现通过外部振动数据推演特高压并联电抗器铁心振动特征的目的，并可以据此对设备的运行状态做出评价。

本文通过现场试验的手段，研究了特高压并联电抗器铁心与油箱外壁振动信号相关性的问题。首先通过理论分析，给出了特高压并联电抗器铁心振动产生与传播机理。然后，借助特高压并联电抗器等效模型开展试验，获得了铁心和油箱外壁各测点的振动数据。通过对比分析选择100 Hz倍频分量作为振动参数，欧氏距离倒数作为信号相关性大小评价指标。研究了特高压并联电抗器铁心振动信号与油箱外壁各测点振动信号的相关性，并从油箱外壁的测点中选择出了与铁心振动参数相关性较高的测点。为后续基于振动信号特征的特高压并联电抗器状态监测与故障诊断打下了基础。

1 特高压并联电抗器铁心振动产生与传播机理

1.1 特高压并联电抗器铁心振动产生机理

特高压并联电抗器铁心的振动机制可以描述为其在麦克斯韦力和磁致伸缩等效应力共同激励下的受迫振动，振动波通过构件(紧固件和垫脚等)或变压器油传递到油箱，进而引起油箱的振动。其中，铁心振动可以用式(1)表示[11]：

(1)

式中：Mc为质量矩阵；uc为位移矩阵；C为阻尼矩阵；Kc为刚度矩阵；F为电磁外力；Fmax为麦克斯韦力矩阵；Fmag磁致伸缩力矩阵；t为时间。

麦克斯韦力是铁心饼与气隙界面处的一种面应力，可以通过麦克斯韦应力张量积分计算：

(2)

式中：Tmax为麦克斯韦应力张量；B为界面处的电磁感应强度矩阵；H为磁场强度矩阵；μ为磁导率矩阵；I为单位矩阵；积分面为铁心饼与气隙的交界面。

磁致伸缩等效应力是铁心磁致伸缩现象的一种等效体应力，可以通过铁心在磁场中的磁致伸缩应变计算获得：

Fmag=-·σ=-·(Dε)

(3)

式中：σ为磁致伸缩应力；ε为磁致伸缩应变；D为弹性张量。

1.2 特高压并联电抗器振动传播机理

变压器油为流体，振动在流体中仅能以纵波的形式进行传播，其波动方程为[17]

(4)

式中：p为波动压力；c为波速；t为时间。

特高压并联电抗器的构件均为固体，振动在固体中既可以传播纵波也可以传播横波，其波动方程为

(5)

式中：λ为拉梅第一常数；μl为拉梅第二常数；s为位移矢量。

此外，铁心振动还可以通过铁心-绕组-变压器油-油箱的路径进行传播，该传播路径既包含流体也包含固体，同时还涉及流-固界面处振动波的折反射，是一个极其复杂的过程，基于数值计算的有限元仿真的方法难以对这一过程进行十分准确的计算[18]。

综上，特高压并联电抗器铁心振动的产生与传播路径如图1所示。

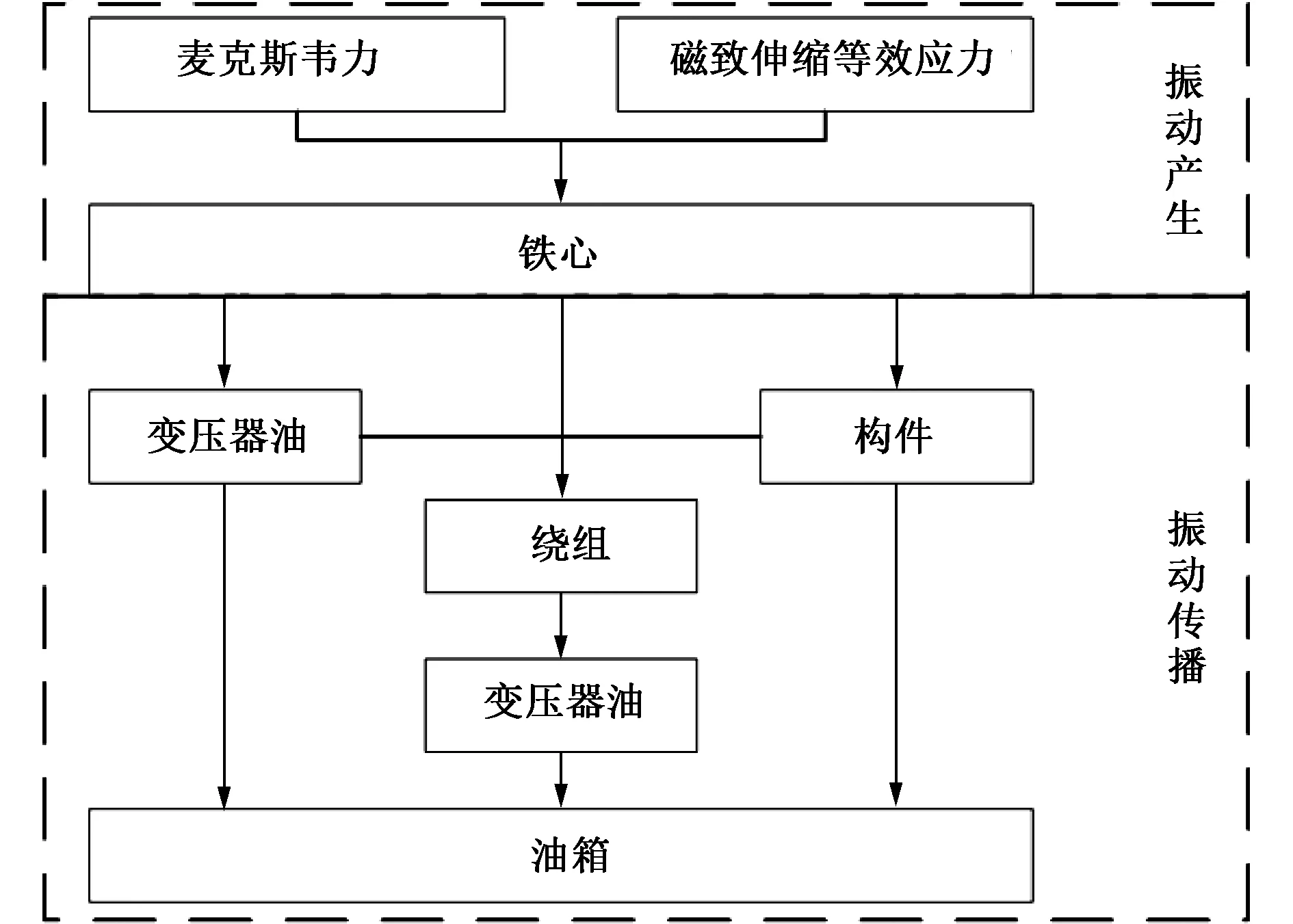
图1 铁心振动的产生与传播路径Fig.1 Generation and propagation path of core vibration

2 基于特高压并联电抗器等效模型的振动信号测量实验

试验在保定天威保变股份有限公司的高压试验大厅内开展，振动测试系统是由江苏东华测试技术股份有限公司开发的DH5902坚固型数据采集系统，采样频率为5 000 Hz，选用的振动传感器参数如表1所示。

表1 振动传感器参数

相关试验经验表明：在电抗器铁心柱处布置振动传感器的难度较大且无法保证测试结果的准确性，故本次试验的5个测点均布置在铁轭部分(如图2所示)，具体位置说明如表2所示。

表2 特高压并联电抗器等效模型测点位置

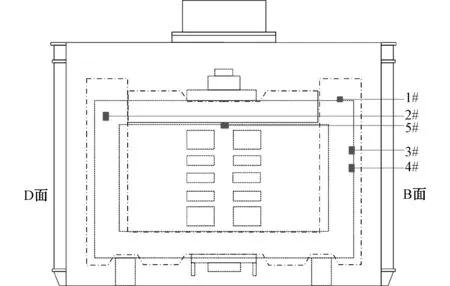
图2 电抗器内部振动测点位置示意图Fig.2 Diagram of internal vibration measuring points location

油箱外部振动测点均匀布置在特高压并联电抗器的4个侧面，如图3所示。

图3 电抗器外部振动测点对应位置Fig.3 Location and identifier of internal vibration measuring points

图3中，阴影为加强筋区域。

对于确定的并联电抗器而言，其运行状态仅与试验电压相关。本文定义试验电压比：

(6)

式中：U为电抗器运行电压；U0为电抗器的额定电压。本次试验依据试验电压的不同共分为8组，电压比分别为：0.8、0.9、1.0、1.1、1.2、1.3、1.4和1.5。记录8组试验电压条件下铁心和油箱外壁的振动数据。

3 振动信号相关性评价方法筛选

3.1 数据预处理方式筛选

通过振动测量系统获得的电抗器内外部振动原始数据的数据量极为庞大，选择合适的方法对原始数据进行预处理，可以在不降低计算准确性的前提下大大提高数据处理的效率。

3.1.1 常用数据预处理方法

(1)时域分量

电抗器的振动信号为周期性信号，因此在分析振动信号相关性时，只需截取1 s的振动信号即可。但时域信号往往只反映信号整体强弱随时间的变化，难以直接表征更多频域信息，且时域信号数据量较大，后续计算量也会随之增大。

(2)频域分量

相较于直接使用时域信息，振动信号的频域信息能够一定程度对信号进行压缩。电抗器的振动信号为周期性信号，因此截取1 s时间段的振动信号进行傅里叶变换即可。数字信号处理中使用离散傅立叶变换(Discrete Fourier Transform, DFT)对离散的信号进行变换：

(7)

式中：w(n)为窗函数。

本文使用具有较好的时间和频率聚集特性的汉明窗(hamming)，能够有效减小因傅里叶变换产生的失真现象，函数表示为

(8)

式中：N为汉明窗的长度；n为噪声信号长度，0≤n；k≤N-1。以电抗器外表面某点振动信号为例，可得到振动信号频域分布图，如图4所示。

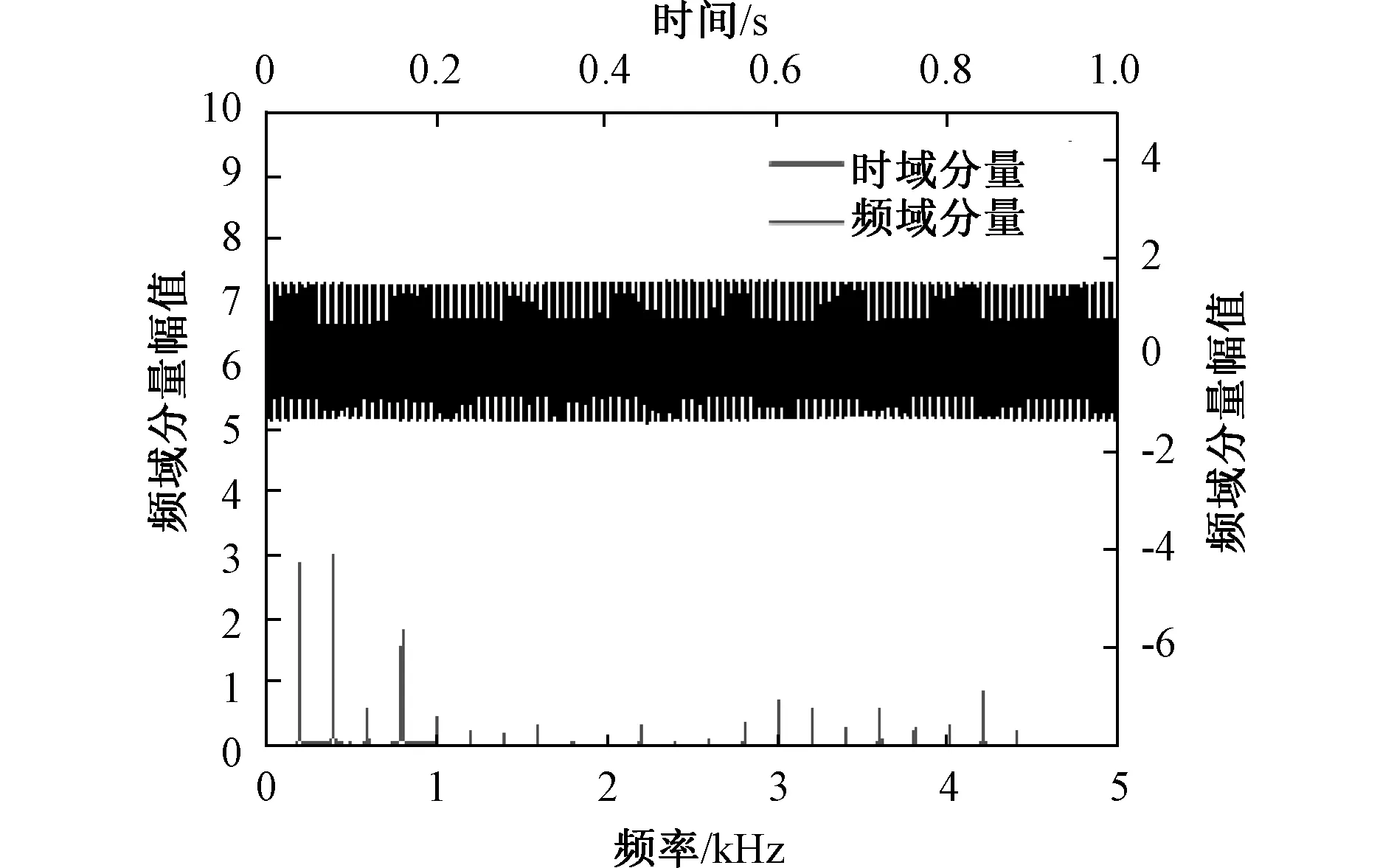
图4 电抗器外表面某点振动信号时域分量与频域分量图Fig.4 Time domain component and frequency domain component of vibration signal at a point on outer surface of reactor

(3)100 Hz倍频分量

从图4及文献[19]中可知，电抗器振动信号主要分布为100 Hz的倍频，因此在经过离散傅里叶变换的基础上，可以只提取100 Hz倍频数据作为振动信号的特征参量用于后续分析。在去除冗余的频点信息后，100 Hz倍频分量能够兼顾特征信息完整性与数据量小优势，在不影响计算准确性的条件下极大的压缩了计算量，适合用于相关性分析。

电抗器内部的振动传递到油箱后，振动信号振幅会衰减，导致内外部测点的振动信号幅值存在一定差异。为了更好地进行相关性分析，需要分别对数据进行归一化处理。归一化处理如下式所示：

(9)

式中：X为位移或噪声同一组实验数据的列向量；xk为每一点频率对应的幅值，k为0～5 000 Hz内的100 Hz的整数倍。

3.1.2 数据预处理方式对比

为了验证时域分量、频域分量、100 Hz倍频分量在计算相关性时的效果，本文以额定电压下的8号内部测点对A面各外部测振点欧式距离倒数分布为例，对三者进行了对比，如图5所示。

从图5看出，时域分量计算得到的相关性数值极低，并不能对各外部测振点的进行有效区分。而100 Hz倍频分量的相关性区分度比频域分量更高，且计算量大幅减少。因此，本文的数据预处理方式选择100 Hz倍频。

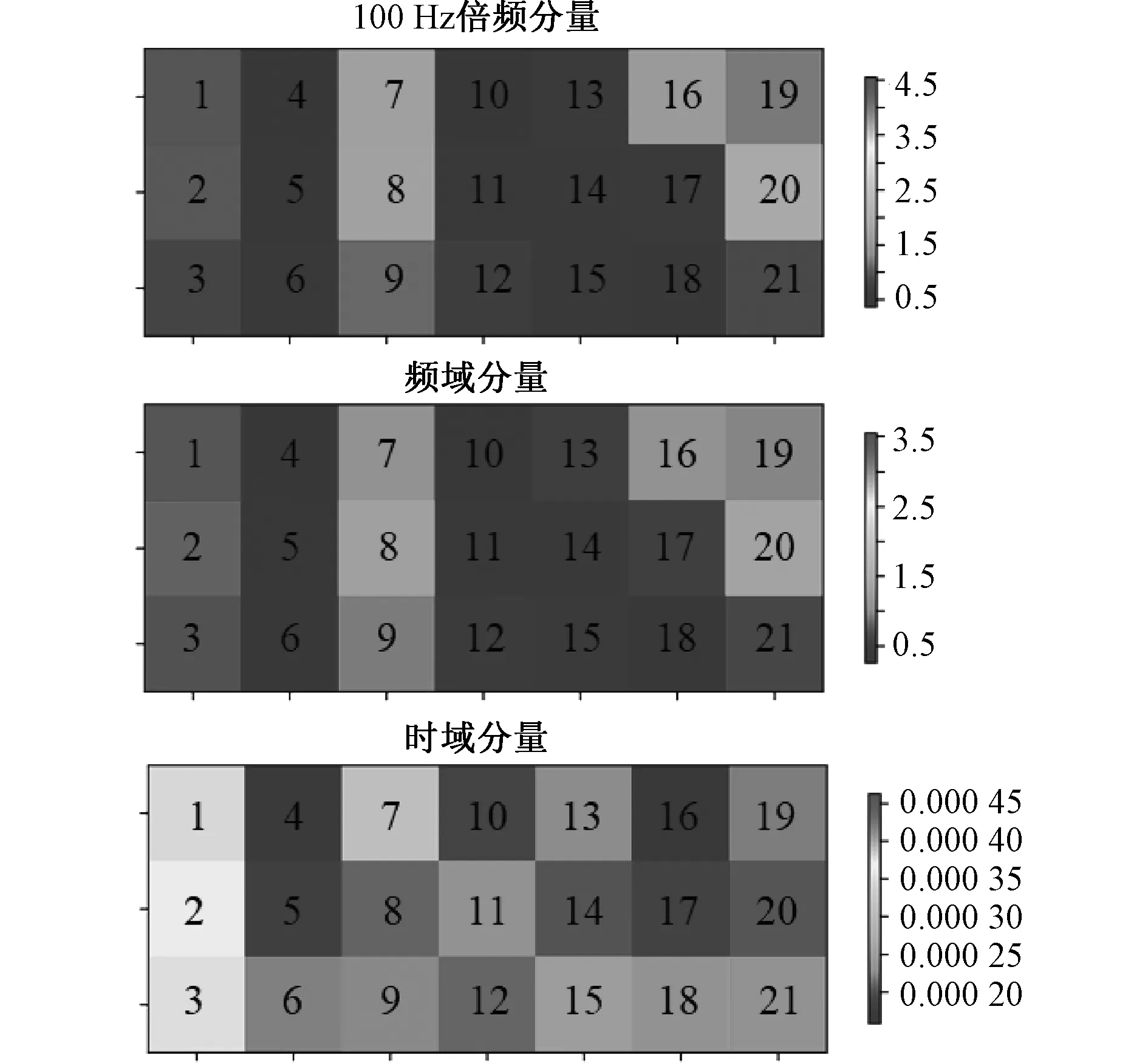
图5 不同预处理方式对相关性计算结果的影响对比Fig.5 Comparison of influence of different pre-processing methods on correlation degree calculation

3.2 相关性指标筛选

相关性指标的种类众多，选择合适的指标有利于后续研究的顺利开展。本文列举现有文献中常见的几类相关性指标，通过对比分析从中选择合适的指标用于开展油浸式并联电抗器内外部振动测点数据的相关性分析。

3.2.1 常见相关系数

(1)皮尔森相关系数[20]

皮尔森(Pearson)相关系数、斯皮尔曼(Spearman)相关系数和肯德尔(Kendall)相关系数是统计学种最常用的三种相关系数。其中，斯皮尔曼相关系数和肯德尔相关系数都是秩相关系数，在计算过程中会依据数据大小对数据进行重新排序，不适合用于电抗器内外部振动数据相关的研究。因此，选择皮尔森相关系数进行研究。

皮尔森相关系数，又称作为相关相似性，可以反映变量之间的相似程度的统计量。通过计算变量数据间的相似度来表征其相关性，其值大小介于-1与1之间，当值为正时，为正相关，绝对值越大，则正相关的程度越大。

归一化后的电抗器内外测振点的振动信号间的皮尔森相关系数定义为

(10)

式中：xik为内部测点i的振动数据；i取1～8，分别代表内部振动测点编号，序号对应位置如表2所示;xjk为油箱外壁测点j的振动数据，j取1～84，分别代表外部振动测点编号，序号对应位置如图3所示;k为100 Hz倍频数，即xik=xi(k×100 Hz)，xjk=xj(k×100 Hz)。

(2)欧氏距离倒数[21]

欧氏距离的数学表述是将空间变量点与变量点之间的差值平方和再求其平方根，体现的是m维空间中数据间的整体真实距离，也代表了数据间的不相似性。其倒数值越大，表征距离越近，相似程度越高。为便于评价电抗器内外振动测点振动信号之间的相关性，本文对100 Hz倍频分量进行欧氏距离倒数计算：

(11)

(3)频域置信因子[18]

FDAC (frequency domain assurance criterion，频域置信因子)是文献[18]中给出的一种用于描述振动信号传递函数相关性的评价指标，其计算公式如下：

(12)

式中：xi(ω)=[xik]，为内部测点振动数据中的100 Hz倍频分量矩阵；xj(ω)=[xjk]，为油箱外壁测点振动数据中的100 Hz倍频分量矩阵。

3.2.2 相关性指标对比

欧氏距离倒数、皮尔森相关系数和频域置信因子都能表征相关程度，因此需要比较三者在振动信号相关性方面的分析效果。以4号内部测点的100 Hz倍频分量为例，如图6所示为电抗器在额定电压运行状态下4号内部测点与外部全部测点之间的3种相关系数对比。

图6 额定电压状态下4号内部测点与全部外部测点相关度分布Fig.6 Distribution of correlation between No. 4 internal measuring point and all external measuring point under rated voltage

由图6可以看出，3种相关性指标呈现的相关性分布图具有一定相似性：以D面为例，3种相关性指标在61、64、65外部测点关联系数均显著高于D面其他测点，在A、B、C面也存在相似规律。

3张分布图也具有很强差异性：皮尔森相关系数和频域置信因子呈现的相关性较为笼统，例如在呈现C面的40～54外部测点相关性时，皮尔森相关系数和频域置信因子均处于较高水平，相关性差异难以区分，而欧氏距离倒数分布图则能更为明显地对相似性差异进行划分。

文献[18]的研究表明：油箱外壁不同位置的振动信号中包含的来自各种传播路径的振动信息并不相同，部分位置受到固体传播的振动信号影响较大，部分位置受到液体传播的振动信号影响较大。本次试验在实验室环境下进行，可以认为油箱外壁的振动完全是由于电抗器内部振动波的传递引起的。选择能够表征油箱外壁各测点包含振动信息差异的相关性指标有助于更好的比较外部各测点之间的差异性，从而能够更加清楚地选择适合用于后续研究的外部测点。

根据以上对比结果，本文选择欧氏距离倒数作为相关性分析指标。

4 并联电抗器内外部振动信号相关性分析

为了分析不同内部测点与外部测点之间的相关性，本文采用欧式距离倒数法对8种不同运行电压情况下振动信号的100 Hz倍频分量的相关性分布分别进行计算，然后对8个运行状态下的相关性取平均值得到最终的综合相关性分布。

以4号测点的相关性计算为例，计算过程如图7所示。从图中可以看出，施加不同电压情况下，各个面的相关性分布均会发生不同程度变化。

图7 4号内部测点与外部测点平均相关性分布计算过程Fig.7 Calculation process of average correlation degree distribution between internal measuring point No. 4 and all external measuring points

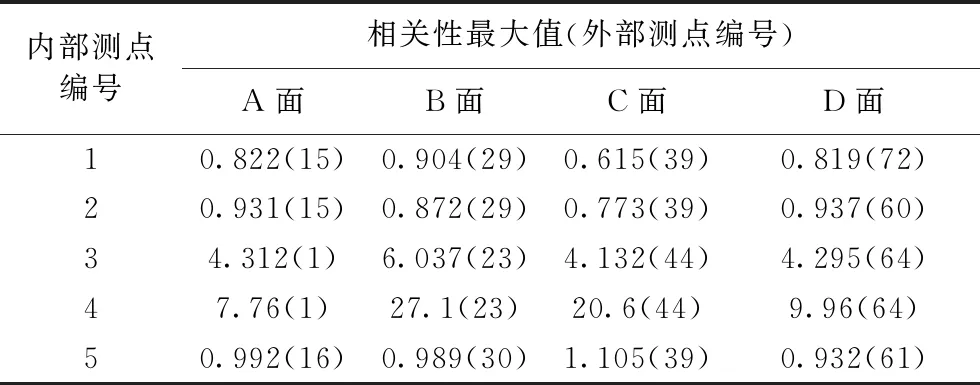
其他内部测点的相关性也使用同样方法进行计算，受篇幅限制，完整计算结果附在附录图A1中。为了方便比较各个内部测点与外部测点的关联程度，本文在表3中罗列了内部测点在油箱各外壁上测点的相关性最大值与对应的外部测点编号。

表3 内部测点与油箱各外壁上测点的相关性最大值

Tab.3 The maximum correlation between internal measuring points and external measuring points

根据表3可知：(1)与内部测点1相关性最强的外部测点是B面的测点29；与内部测点2相关性最强的外部测点是D面的测点60; 与内部测点3相关性最强的外部测点是B面的测点23; 与内部测点4相关性最强的外部测点是B面的测点29; 与内部测点5相关性最强的外部测点是B面的测点39;这些外部测点均位于油箱的窄面(B面或D面)。(2)由表2可以看出，3号测点和4号测点的相关性最大值显著高于其他点，1、2、5三个内部测点与任意外部测点之间的相关性都非常低，换言之，从外部的任意测点进行振动信号测量都难以反映1、2、5号三个位置的振动信号。(3)除去61号测点(位于加强筋上)是1号测点在D面的最大相关测点外，其余各最大相关测点均位于非加强筋位置。

观察1、2、5号三个测点位置可以发现，以上三处的测点在被测平面上的法线均不垂直4个外壁平面；而3号测点和4号测点在被测平面上的法线均垂直于B面，例如：4号内部测点与23号外部测点的振动信号相关性最高，而23号外部测点正位于4号测点的法线与B面的相交位置；

综上所述，可以得出以下结论：(1)电抗器内部振动能够一定程度地传播到油箱外壁上，内部振动点与外部振动测点之间的传播路径越直接，内外振动信号相关性越高，越能从外部振点获取选定的内部振点的振动规律。(2)在选择外部测点时应尽可能布置在非加强筋位置。

5 结 论

本文通过现场试验的方法，测量获得了特高压并联电抗器等效模型铁心和油箱外壁的振动数据，筛选了100 Hz倍频分量作为振动参数，欧氏距离倒数法作为评价指标，通过相关性分析研究了特高压并联电抗器内外部振动数据之间的相关性，为后续特高压并联电抗器外部振动测量的选点提供了参考意见。主要得出如下结论：

(1)与时域和频域分量相比，振动信号的100 Hz倍频分量更加适合用于振动信号的处理，可以有效消除其他信号的干扰；欧式距离倒数与皮尔森相关系数和频域置信因子相比，能够更好地反映油箱外壁各测点获取的内部振动信息之间的差异，更加适合用于大型油浸式并联电抗器内外部振动数据相关性的研究。

(2)电抗器内部振动能够一定程度地传播到油箱外壁上，内部振动点与外部振动测点之间的传播路径越直接，内外振动信号相关性越高，越能从外部振点获取选定的内部振点的振动信息。

(3)与通过其他路径传播的振动信号相比，通过液体路径直接传播至油箱外壁的振动信号与铁心振动信号的相关性较高，可以通过测量油箱外壁振动信号的手段评估铁心与油箱垂直相对位置处的振动状态，而对于铁心其他位置则不宜采用此类方法。

(4)油箱外壁未布置加强筋的位置较加强筋位置更适合用于油浸式并联电抗器内部振动数据的间接测量。

上述研究结论对于后续基于特高压并联电抗器油箱外壁振动信号的在线监测和故障诊断具有积极意义。在后续研究与工程实践中，可以根据本文结论选择合适的振动测点，服务于基于油箱外壁振动信号的油浸式并联电抗器在线监测与故障诊断，避免由于盲目选点可能造成的诊断误差与传感器资源浪费。