基于改进堆栈自编码器的变压器故障诊断模型

赵冬梅， 王 闯， 马泰屹

(华北电力大学 电气与电子工程学院，北京 102206)

收稿日期：2020-06-12.

0 引 言

变压器是电力系统中最重要的元件之一，变压器的安全稳定运行是电力系统稳定运行的前提。变压器发生故障后，会给电力系统极大的冲击，威胁系统的安全稳定运行，造成极大的经济损失。因此，有效地识别变压器故障成为了国内外研究的热点，具有重要的理论和现实意义[1, 2]。

目前，变压器故障诊断多采用油中溶解气体分析(Dissolved Gas Analysis，DGA)，通过分析变压器油中各类气体含量来判断变压器的运行工况[3, 4]。传统变压器故障诊断方法包括三比值法[5]、模糊理论法[6]、专家系统法[7]等。但是三比值法存在判定方法过于绝对、故障界限模糊等缺点;基于模糊理论的变压器故障诊断方法较难确定隶属函数，并建立模糊诊断理论需要大量故障数据;基于专家系统的判别方法通常需要丰富的专家知识和经验，而在实际应用中很难获取相应的经验[8]。

随着人工智能算法的发展，出现了越来越多适用于变压器故障诊断的智能算法[9]。基于神经网络的DGA故障诊断方法主要包括两大类，第一类为有监督学习，包括支持向量机[10]、BP神经网络[11, 12]和极限学习机[13]。传统的人工智能算法过于依赖有标签的故障数据，变压器故障诊断中存在大量无标签数据，并且因为数据维度远低于数据样本量，神经网络存在过拟合的情况，自编码器的应用可以很好的解决这样的问题。文献[8]提出一种构建多层自编码器的神经网络，逐层对自编码器进行训练，提高了网络的鲁棒性和分类的准确率；文献[14]提出了一种基于堆栈稀疏降噪自动编码器，使得隐藏层中的神经元多数处于抑制状态，少数处于激活状态，并在输入数据中加入噪声，增强了网络的诊断性能。文献[15]基于k步对比散度算法，利用大量无标签样本对故障诊断模型中的每个受限玻尔兹曼机进行无监督训练，结果表明网络诊断性能优于支持向量机和反向传播神经网络。

考虑到变压器样本数据含有大量无标签数据，并且数据维数远小于数据样本数的情况，本文提出了一种改进堆栈自编码器的变压器故障诊断模型，将批量标准化引入自编码器，经算例分析，相比于堆栈自编码器，改进自编码器增强了的训练效果，提高了网络的诊断性能。

1 DGA故障诊断原理

DGA可以分析变压器油中不同种类气体的含量。变压器在故障发生前后油中溶解气体的含量会迅速发生变化。本文选用氢气(H2)、甲烷(CH4)、乙烷(C2H6)、乙烯(C2H4)、乙炔(C2H2)五种气体作为变压器故障诊断的依据。变压器故障可以分为热性故障、电性故障以及放电兼过热故障。其中，热性故障通常分为高温过热和中低温过热，电性故障分为高能放电、低能放电和局部放电。表1对变压器中存在的故障状态进行了编码，包含正常情况在内一共有7种。

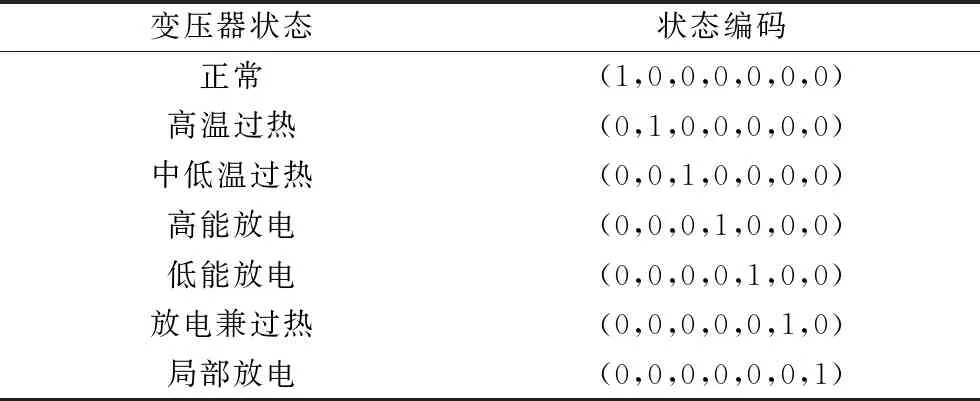
表1 变压器状态编码

2 改进堆栈自编码器

2.1 堆栈自编码器

自编码器是一种能够通过无监督学习，学到输入数据高效表示的人工神经网络。在图像识别领域中，自编码器一般用于对数据进行降维，加速特征提取过程，大大缩短训练时间。通过分析变压器油色谱，我们可以判断变压器的运行工况。变压器故障数据维度远小于故障样本数，特征信息不够丰富，于是通过自编码器网络对数据进行升维[16]。

网络中，编码器对输入数据进行编码，经变换后可以得到原始信息的另外一种特征表示。为了判断经编码后的信息能否代表数据的特征，需要解码器对编码信息进行还原，若还原后能得到与原始信息相同或相似的信息，则可以说明编码器有效，经过编码的数据能够代表原始数据。编码过程可以用式(1)表示，解码过程可以用式(2)表示。

h=f(W1x+b1)

(1)

y=f(W2h+b2)

(2)

式中：x为输入向量;h为隐藏层输出的中间向量;y表示输出向量;f(·)表示编码层和解码层的激活函数;W1和W2分别表示编码层和解码层的权重矩阵;b1和b2分别代表编码层和解码层的偏置向量。

自编码器的目标函数是使得输入数据和输出数据尽可能相似，误差函数选为均方误差，表达式如下：

(3)

式中：n表示输入样本数。

当自编码器的编码层和解码层的隐藏层数量大于1时，AE就是通常所说的深度结构，形成了堆栈自编码器(stack auto-encoder,SAE)。SAE的拓扑结构如图1所示。

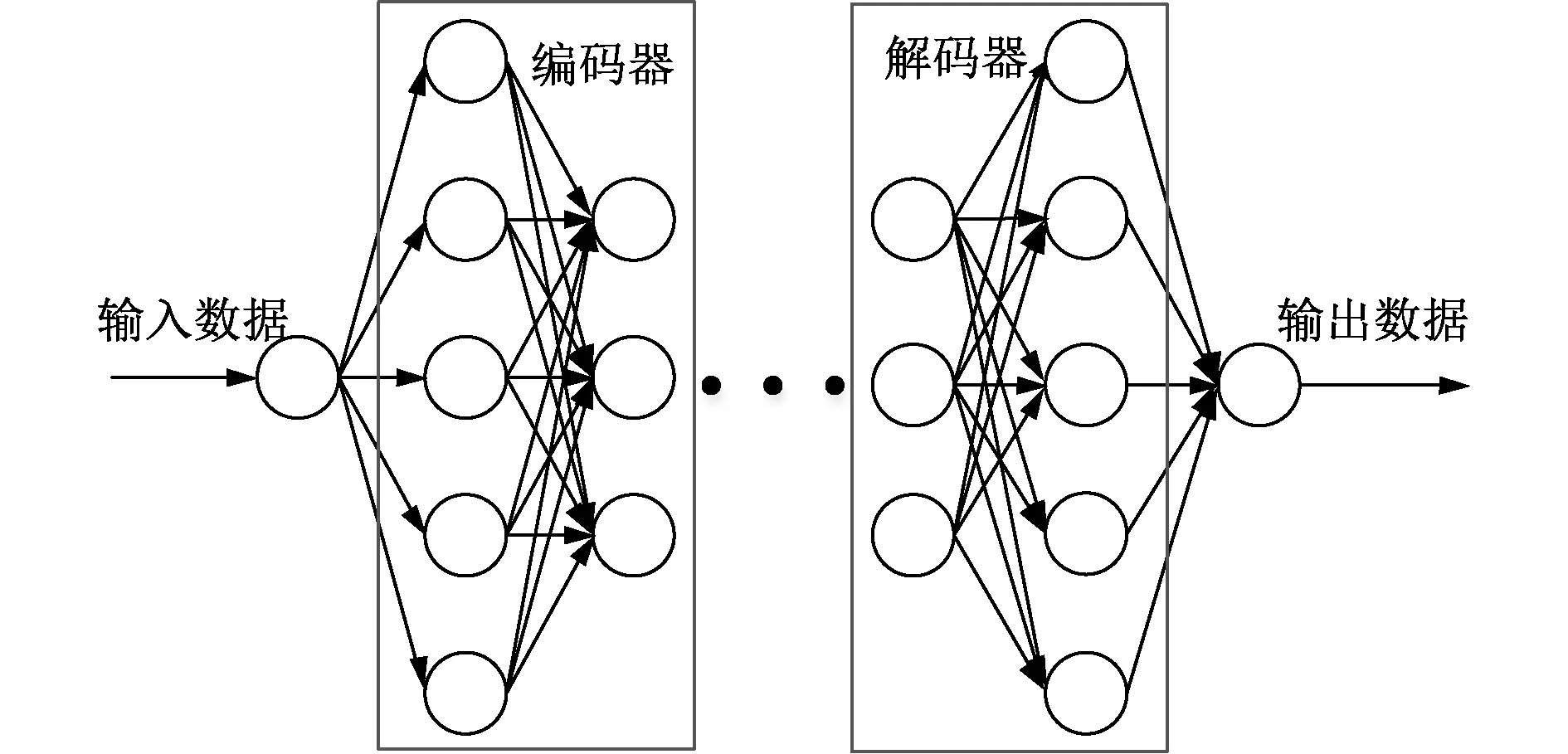
图1 SAE拓扑结构图Fig.1 SAE topology diagram

2.2 批量标准化

神经网络进行分类时，需要满足训练数据和测试数据独立同分布。深层神经网络经过隐含层变化后，分布逐渐偏移，当整体分布逐渐往非线性函数的取值区间的上下限两端靠近时，会导致反向传播时低层神经网络的梯度消失，使得训练收敛速度慢。BN的作用就是使训练中每一层神经元的输入分布相同，提高神经元灵敏度。

神经网络通过激活函数对数据进行非线性变换，以Sigmoid函数为例，Sigmoid函数图形如图2所示。中心区域导数值较大，边缘区域导数值较小。若未经批量标准化，隐藏层的输入数据仅少部分落入到函数的敏感区间，大部分数据落入到了函数的不敏感区间。神经网络层数加深后，会出现梯度消失的情况，使得网络训练速度变慢，效果变差。

图2 Sigmoid函数Fig.2 Sigmoid Function

批量标准化的过程与数据预处理中对数据的标准化过程类似，通过计算输入隐藏层数据的均值和方差，对数据进行标准化处理。

(4)

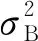
变换后每个神经元的输入形成了均值为0，方差为1的正态分布，目的是让数据落入激活函数的敏感区域，增大导数值，增强反向传播信息流动性。为了避免输出变为输入的线性组合，导致网络表达能力下降，每个神经元增加两个调节参数，这两个参数是通过训练来学习到的，用来对变换后的激活反变换，使得网络表达能力增强[17]，这其实是变换的反操作：

(5)

式中:γ和β为调节参数，避免神经网络线性化。

2.3 改进堆栈自编码器

为了使AE中每层输入保持相同的分布，加强AE的训练能力，改进堆栈自编码在每一层编码器和解码器前，引入了批量标准化操作，对每一层的输入做标准化处理。具体流程如式(6)～(8)所示:

h=f(W1x+b1)

(6)

h′=BN(h)

(7)

y=f(W2h′+b2)

(8)

式中:h′指中间变量标准化后的值;BN(·)表示批量标准化。

改进堆栈自编码器的拓扑结构如图3所示。

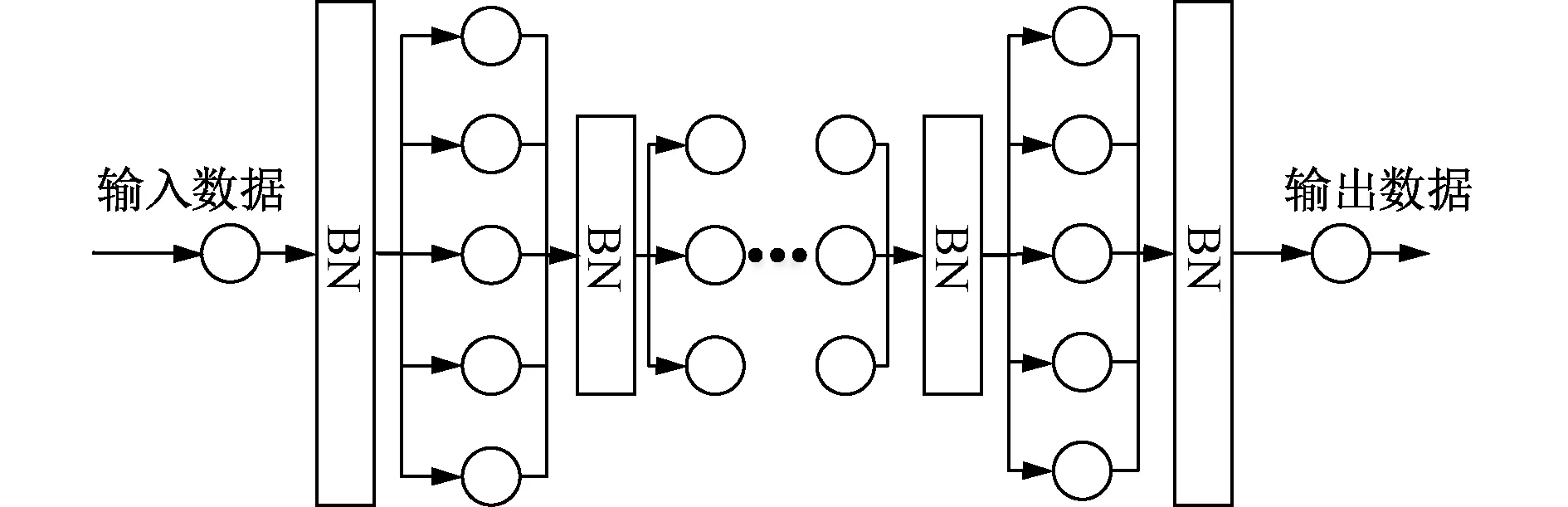
图3 改进AE拓扑结构图Fig.3 Improved AE topology diagram

2.4 基于改进堆栈自编码器的变压器故障诊断流程

由于变压器无标签数据较多，并且存在数据维度远小于数据样本量的特点，需要使用自编码器对数据进行预训练，诊断流程如下：

步骤1:构造改进堆栈自编码器的结构，确立隐藏层节点数以及隐藏层层数，初始化权重W和b。

步骤2:将无标签变压器数据输入网络，每经过隐藏层计算一次，就需要重新对数据标准化处理，最后得到网络输出值，计算均方误差。

步骤3:由均方误差进行梯度反向传播，更新网络参数。

步骤4:重复步骤(2)、(3)，直到达到最大迭代次数或均方误差小于规定值。

步骤5:输入有标签的变压器故障数据对网络进行微调，使网络参数分类效果达到最佳。

步骤6:输入测试集数据验证网络的有效性。

故障诊断流程图如图4所示。

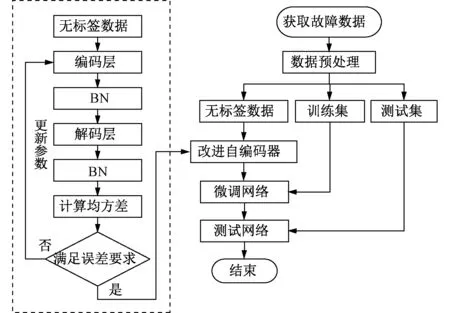
图4 基于BN-SAE的变压器故障诊断流程Fig.4 Transformer fault diagnosis flow based on BN-SAE

3 算例分析

3.1 数据预处理

本文选用IEC TC 10数据库[18]中的变压器故障数据和某单位提供的变压器故障数据，其中无标签数据450组，故障数据共210组，本文将数据按照2∶1的比例分为训练集和测试集。根据DGA数据特点，选取 H2、CH4、C2H6、C2H4和 C2H2这5种特征气体的含量作为神经网络的输入项，样本样例格式如表2 所示。

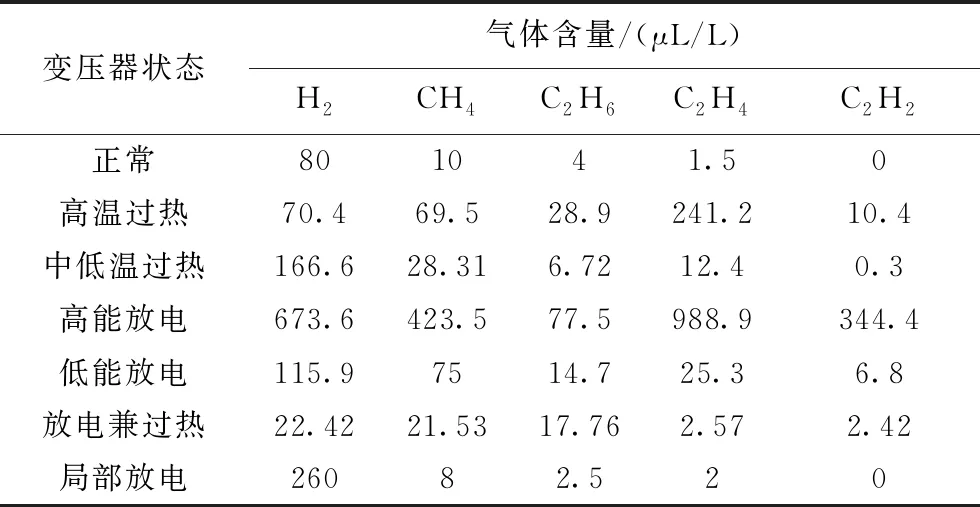
表2 变压器故障数据样本

如表所示，不同故障中气体含量差别十分大，为了增强网络的训练效果，将输入数据进行标准化处理，公式如下：

(9)

式中：xnew为标准化之后的值，x表示原样本;xmean表示样本的平均值;xmax表示样本的最高值;xmin表示样本的最低值。

3.2 参数测试与分析

本文选用的编程环境为Python3.6，处理器：i3-550，运行内存：4G，操作系统：64位Win7。

首先，对单层AE网络中参数进行测试分析，选出合适的隐藏层数目。AE网络中参数设置为:最大迭代次数为1 000，学习率为0.005，网络连接权重W和偏置系数b采用正态分布初始化。

(1)激活函数的确定

神经网络常用的激活函数有Relu函数，tanh函数，Sigmoid函数,自编码器采用不同训练函数的均方误差如表3所示。

表3 三种激活函数均方误差比较

由表我们可以看出，当激活函数采用tanh函数时，自编码器的均方误差最小，最能够保留原始数据信息，因此本文采用tanh作为激活函数。

(2) 隐藏层节点数

通过改变单层AE的隐含层节点数计算均方误差，并根据均方误差的大小来判断最优的隐含层节点数。

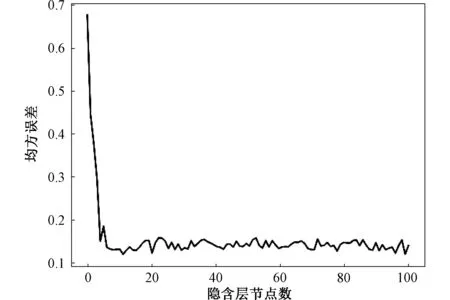
图5 AE训练误差与隐含层节点数的关系图Fig.5 Relationship between AE training error and number of hidden layer nodes

由图5可以看出，均方误差在隐藏层节点数为50时基本达到稳定，不再随着节点的增加而降低，于是本文AE采用50个节点的隐藏层。

(3)隐藏层层数

通过改变AE层数来寻找最优的隐藏层层数，设定SAE的各隐藏层的节点数为50，25，15，10，5，用变压器无标签数据对网络进行训练，所得均方误差如图6所示。

由图6可知，当隐含层层数为2层时，AE的训练误差达到最小。当隐藏层层数大于2时，网络训练误差反而增大，这是因为隐含层层数增加，会增加损失的信息，进而导致误差增大。并且变压器原始数据维度过低，采用过多的隐藏层并不能使训练效果更好，因此本文采用隐含层含量为2层的堆栈自编码器。

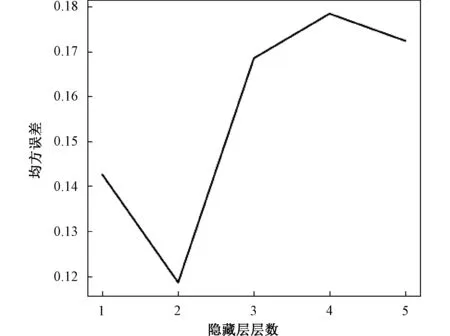
图6 AE训练误差与隐含层数量的关系图Fig.6 Relationship between AE training error and number of hidden layers

3.3 结果测试与分析

本文首先对比了在同等隐含层层数、隐含层节点数以及其它参数均相同的情况下SAE与BN-SAE的均方误差值。比较结果见图7。

如图7可见，BN-SAE的RMS误差下降的更快，在600次训练后基本达到稳定，较自编码器少训练100次左右。并且，BN-SAE的RMS误差更小，表明引入批量标准化后，编码器能对原始信息作出更好的编译，在对数据特征重构的同时，尽可能的保留了原始信息。

图7 SAE与BN-SAE训练的均方根误差比较Fig.7 Comparison of root mean square error between SAE and BN-SAE

然后用450组无标签数据对改进堆栈自编码器进行训练，之后用100组有标签变压器故障数据对网络进行微调，最后用70组有标签变压器故障数据对网络诊断性能进行测试。

并且本文设立了几个对照组，分别为堆栈自编码器、自编码器以及BP神经网络。堆栈自编码器与改进自编码器除批量标准化外其余结构均相同。自编码器采用单层结构，参数设置与改进自编码器相同。BP神经网络的学习率与隐含层数量与自编码器相同。

图8 基于BN-SAE的变压器故障诊断Fig.8 Transformer fault diagnosis based on BN-SAE

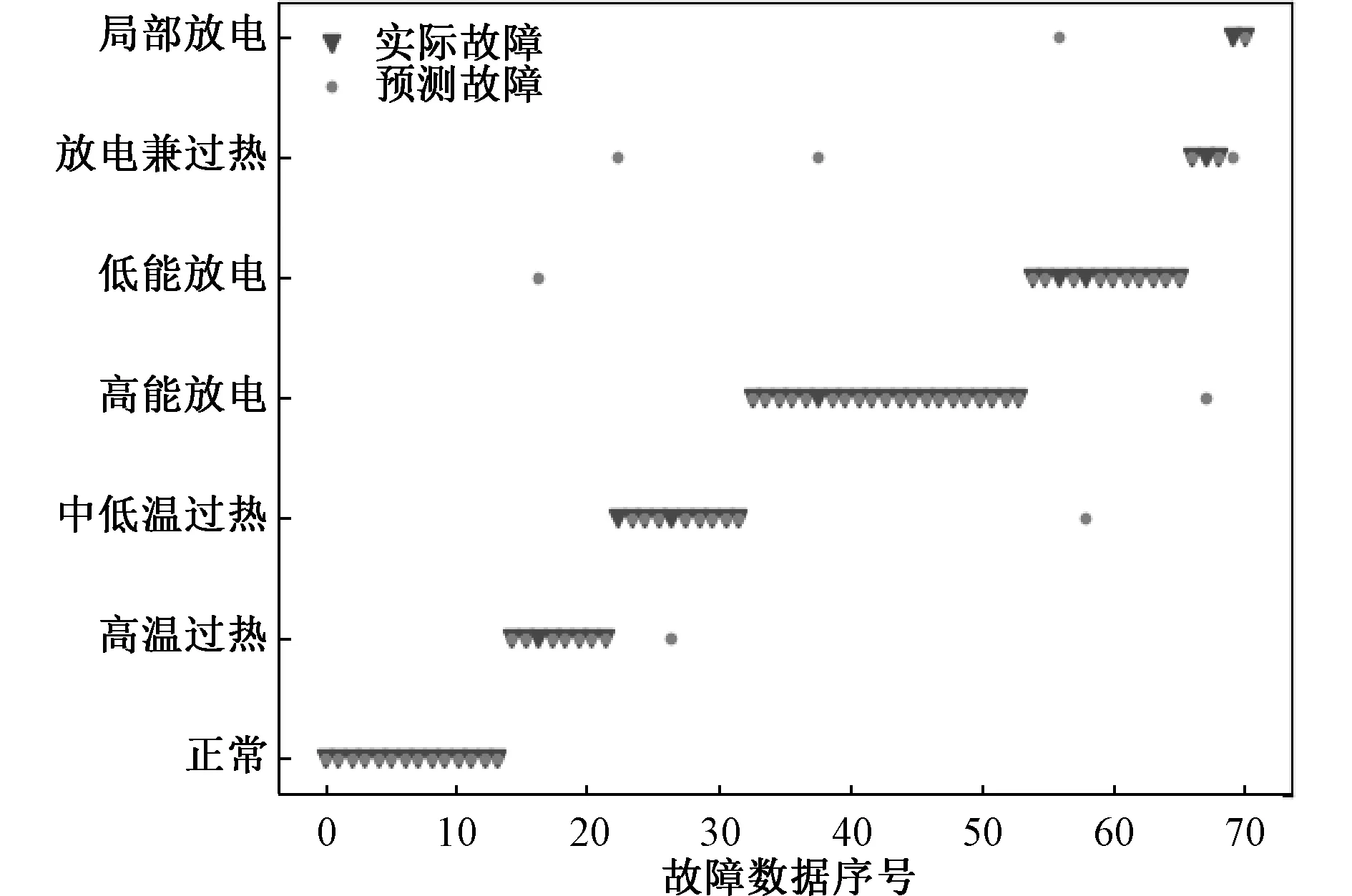
图9 基于SAE的变压器故障诊断Fig.9 Transformer fault diagnosis based on SAE

通过比较图8和图9可以看出，BN-SAE的诊断性能更好，特别是针对少数类样本的故障诊断，如放电兼过热故障和局部放电故障时精度较高。SAE的诊断误差相对较高，并且针对少数类故障样本的分类效果不好。

表4列举了4种不同网络的分类准确率，可以看出BN-SAE的诊断正确率最高，高于SAE和AE，其次带有自编码器的网络预测准确率均高于BP神经网络，证明了自编码器用于变压器故障诊断的有效性。

表4 不同方法故障诊断精度比较

4 结 论

针对变压器故障诊断的特点，本文通过将批量标准化引入SAE，来改进自编码器在变压器故障诊断领域的应用效果。通过对输入隐藏层数据的标准化操作，使得数据处于激活函数的敏感区域，加快了训练速度，增强了训练效果。仿真算例表明BN-SAE的训练误差更小，对无标签数据的利用度更高，可以更好的表示变压器原始数据，并且网络的诊断精度更高。BN-SAE相比于SAE与AE，在变压器故障诊断中的准确率分别提高了4.29%和8.57%。并且BN-SAE网络的鲁棒性较强，训练稳定性较好，是一个有效的变压器故障诊断模型。