城轨车用复合动力储能系统蓄电池SOC和SOH估计
2020-12-15郭佑民戴银娟付石磊
郭佑民,戴银娟,付石磊
城轨车用复合动力储能系统蓄电池SOC和SOH估计
郭佑民1, 2, 3,戴银娟1, 2, 3,付石磊1, 2, 3
(1. 兰州交通大学 机电技术研究所,甘肃 兰州 730070;2. 甘肃省物流及运输装备信息化工程技术研究中心,甘肃 兰州 730070;3. 甘肃省物流与运输装备行业技术中心,甘肃 兰州 730070)
以城市轨道交通复合储能系统蓄电池荷电状态(SOC)和健康状态(SOH)估算为目的,采用适合城市轨道交通车辆运行工况的二阶RC等效电路模型,并通过遗忘因子最小二乘算法(FFRLS)辨识其模型参数。基于二阶RC等效电路模型利用传统的自适应无迹卡尔曼滤波算法(AUKF)估计电池的荷电状态(SOC),由于列车复杂的运行环境,其电池受到的噪声是一个动态变化值,因此导致其估算结果误差较大,其最大误差达到5.5%。因此本文采用自适应无迹卡尔曼滤波算法实时估算蓄电池SOC,欧姆内阻及其容量,并根据欧姆内阻、容量与蓄电池SOH之间的函数关系,估算出电池的SOH。最后,通过设定的工况下对状态估计算法验证,经实验分析表明,相比UKF算法,AUKF算法能同时实时循环估算SOC和模型参数,根据观测值可以自动更新噪声,因而对于列车实际运行工况下其实用性更好,且精度较高,其最大误差为3.5%,均差为1.5%。
蓄电池;荷电状态;健康状态;二阶RC等效电路模型;自适应无迹卡尔曼滤波
随着城市的发展,市区人口逐年增加,路面交通拥堵严重影响市民生活和工作,此外,机动车数量的爆发式增长导致环境质量下降,从而导致了雾霾等恶劣天气。城轨交通因具有快速便捷、舒适、安全和运量大等优势愈发受到人们的青睐。目前,城轨列车主要是全程架设接触网,列车通过电力驱动的形式运行[1]。接触网供电不仅成本高,并且容易引发安全事故,在市区架设接触网严重影响城市的美观,特别是在一些旅游景区、繁荣的中心商务区,此外,城轨列车停靠的站点与站点之间距离较短,车辆须要不断地启动、制动,在制动时会产生大量的制动能量,据统计,城轨列车在制动时产生的能耗占总驱动能耗的31%~67%,这无疑浪费了大量的能量,如果能将制动能耗重新回收利用给列车供电,便可以节约10%~30%的电能[2]。因此,无接触网供电城轨车辆应运而生[3],弥补了传统接触网车辆的不足,延伸了城市轨道交通的无网区域运行范围,避免了城市中由于密集接触网线路造成的视觉污染问题,不存在接触网供电可能发生的故障问题,提高了车辆运行的可靠性。蓄电池老化程度直接影响列车的运行状况,其内部状况主要包括荷电状态(state-of-charge,SOC)和健康状态(state- of-health,SOH)[4],其中,SOC表征的是电池的剩余电量,SOH表示电池的健康状况[5-6],目前国内外研究学者主要通过电池的容量、内阻特性、电池的充放电行为及其循环次数3个方向[7]来研究电池的SOH。蓄电池SOC常用的研究方法有安时积分法、开路电压法、神经网路模型和基于模型的状态观测器等[8]。安时积分法(Ah积分)相比较简单,是在已知初始SOC值SOC0的前提下,且对其依赖性较大,SOC及测量的电流都会存在或多或少的误差,并且会随着时间延长误差越来越大;开路电压法利用蓄电池的开路电压(OCV)和SOC之间的函数关系,由OCV的值预测得到SOC,该方法需将电池提前静置较长一段的时间,不适用于实际运行列车的实时估算;神经网络算法依靠较多的样本数据,估算的精度以及运算量依托于训练方法;基于模型的观测器方法是通过电池的空间状态模型,并利用算法递推迭代运算得到,该方法依赖于模型的精确度。SOH预测研究方法主要包括基于电池特征分析、模糊控制、数据驱动等方法[9]。基于电池特征分析是通过基本特征,如利用电池的容量、内阻等与电池充放电循环次数之间的关系,从而预测电池的SOH;模糊控制是将输入的确定值模糊化处理,其规则建立较为困难,且估算结果受模糊规则的影响较大,一般适用于电池电化学模型的内部参数分析;数据驱动常用的方法有神经网络、支持向量机、KF算法等,但该方法对建立的电池的空间状态模型有一定的依赖性,但能对电池的状态定性定量分析,随着列车运行环境较为复杂且多变,列车储能系统受到的干扰噪声无法保持一个定值,而自适应无迹卡尔曼滤波算法根据观测值与预测值之间的误差实时更新观测及系统噪声,因此该方法更适用于列车储能系统的电池状态估计中[11]。针对目前蓄电池状态估计在精度及实时性等方面不够理想的问题,本文综合考虑影响电池SOC估计的因素,选取适用于蓄电池的二阶RC等效电路模型,并通过自适应无迹卡尔曼滤波算法(adaptive unscented Kalman filter,AUKF)估算电池的SOC。自适应无迹卡尔曼滤波算法是将无迹卡尔曼滤波算法(UKF)和扩展卡尔曼滤波算法(EKF)相结合,采用循环迭代的方法计算电池的SOC和参数值,能够实时计算更新电池的模型参数,克服了电池在使用时是一个时变系统的难题,该方法能够实时计算更新模型参数的同时也提高了SOC估计的精度。通过欧姆内阻的大小可以反应电池的SOH,本文通过电池的外部电压情况,基于二阶RC等效电路模型的特点,验证了AUKF算法估计电池SOC和内阻的可行性,并对比UKF算法,证明了该算法估计SOC的精确度更高。
1 建立蓄电池等效电路模型
1.1 蓄电池等效电路模型建立


图1 二阶RC等效电路模型
根据图1所确定的本文中采用的等效电路模型,得到该模型的状态方程如下:

1.2 模型参数辨识
由Ah积分法可得到蓄电池SOC,其计算过程如下:

其中:为库伦效率系数;Q为电池额定容量。
综上可得到本文所构建的蓄电池状态空间模型为:


其中:

式中:v为观测噪声;w为系统噪声。
本文研究的对象为国内某公司生产的锂电池,其最大电压为4.2 V,标称电压为3.6 V,标称容量10 Ah,在1.5 A的恒流模式下进行充电,直到其电压达到4.2 V,然后继续在恒定电压下对其进行充电,直到充电电流降至20 mA。在恒电流为2 A的水平下进行放电,直到锂离子电池的电压降至2.7 V。实验具体电流、电压工况如图2所示。

图2 锂电池设定工况过程
针对复杂的时变系统,应用最多的是用最小二乘算法(Recursive Least Square,RLS)来辨识模型的参数,但是随着新数据的增多,新数据的信息得不到利用,估算的准确性下降,因此,本文选用引入新旧数据比重的遗忘因子最小二乘算法(Forgetting Factor Recursive Least Square, FFRLS)[12]来估算参数值,即利用权重因子来削弱旧数据所起的作用,从而提高新的数据的作用,其性能指标为:

由此得到FFRLS估计公式如下:

将上文中建立的蓄电池二阶等效电路模型状态方程式(1)拉氏变换处理得到如下的关系式:



令:

则式(8)可化简为:

即,求解出参数,,和可得到模型的参数值。
由上述的FFRLS辨识得到的本文中确定的该锂电池模型的参数如图3所示,并取其平均值作为本文所建立的模型参数:1=0.006 37 Ω,1=6 547,2=0.000 53 Ω,2=15 125。

图3 锂电池参数辨识结果
1.3 模型验证
基于上文中采用的锂电池二阶RC等效电路模型,以及通过FFRLS辨识得到的参数值,在Simulink平台搭建的电路仿真模型如图4所示,通过对Simulink模型运行调试得到的电压值与实际值的对比,验证模型的准确性。
本文采用上文中设定的锂电池工况充放电实验过程对选用的模型验证,并将电流作为模型的输入量,得到该模型仿真电压,并将仿真得到的电压值和实际的电压值进行对比分析。如图5所示为电压对比图,图6为误差曲线。
2 AUKF估计锂离子电池SOC
2.1 UKF估计电池SOC
2.1.1 UKF算法原理
无迹卡尔曼滤波(Unscented Kalman Filter,UKF)[13]是为了提高非线性系统的估算精度,Julier等提出了UKF算法,该算法不同于EKF算法,无需对非线性系统采取线性化处理方式,通过增加UT变换解决非线性问题,经过UT变换后再结合KF算法框架便得到UKF框架。相比EKF算法,避免了在线性化过程中将Taylor公式展开的高阶项忽略不计带来的估算误差较大问题,有较高的估算 精度。

图4 锂电池Simulink模型

图5 实测电压与模型电压对比

图6 模型仿真电压误差结果
UKF算法主要是实现UT变换,UT变换是在在状态变量周围选择采样点,且每一个采样点都需要满足该采样点与状态变量二者的均值和协方差及状态变量相等的要求,并将采样点代入非线性方程,由计算出的函数值求得经过UT变换之后的均值和协方差。
2.1.2 UKF算法流程
由于城轨车辆在实际运行环境存在不确定性因素,根据其储能系统蓄电池在退化过程为非线性波动现象,因此假设非线性系统描述如下[14]:

其中:为状态方程函数;为观测方程函数;为状态变量。
1) 选择2+1个sigma点,其选取方式如下:

2) 加权系数:

3) 状态更新:

4) 测量更新:

5) 电池状态变量和协方差估算:
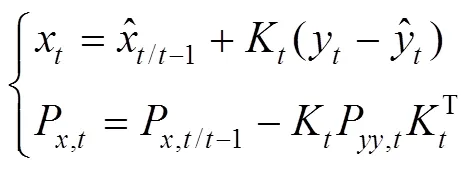
2.1.3 基于UKF估计电池SOC
根据上述建立得等效电路模型以及式(3)~(4)确定得电池系统空间状态方程,结合UKF算法步骤,得到UKF估计电池SOC过程如图7所示。
2.2 AUKF算法估计SOC
自适应无迹卡尔曼滤波算法(Adaptive Unscented Kalman Filtering,AUKF)[15]是依据观测电压和预测电压的误差实时的更新观测和系统噪声,从而减少由于模型误差带来的影响。本文中基于AUKF算法估算SOC结合了锂离子电池的状态及模型参数的估算方法,利用循环迭代方法估算电池SOC,首先根据模型的参数来估算电池的SOC,再由估算出的SOC值计算参数,以此递推循环计算。具体AUKF算法估算SOC流程如图8所示。

图7 UKF算法估计SOC流程图

图8 AUKF估算SOC流程图
3 实验结果验证
为了验证AUKF算法估算电池荷电状态SOC的可行性和准确性,本文基于搭建的二阶RC等效电路模型,在相同的条件下,分别利用UKF算法和AUKF算法估算锂离子电池SOC结果如图9所示,通过精确计算电流积分得到SOC的参考值,其误差结果如图10所示,由图9可知,UKF和AUKF算法均能较好地跟踪预测电池的SOC,但随着时间累积,UKF算法明显出现误差较大的情况。从图10可以看出,AUKF算法估计得到的SOC的误差在3.5%以内,其均差在1.5%,而UKF算法估算结果误差在5.5%以内,均差在3%,因此,AUKF算法估算SOC的精确度明显高于UKF算法。

图9 锂离子电池SOC估算结果

图10 AUKF和UKF算法估计SOC误差比较
4 SOH估计
锂电池的SOH一般指的是其使用寿命长度,电池的容量会随着充放电循环次数的增加不断减小,当蓄电池的实际容量衰减到标称容量的80% 时[16],即认为该电池处于失效状态,可对电池更换,因此电池的实际容量为健康状态的重要评价指标之一,此外,电池的欧姆电阻会随着电池的使用逐渐增大,从而达到电池的失效状态,即欧姆内阻是评价电池SOH的另一重要指标[17]。综上,随着充放电次数的不断增加,电池的失效标准如下:

根据电池的容量和欧姆内阻2个评价指标,其SOH的计算公式如下:
1) 以电池容量为评价指标定义

根据电池的容量定义的SOH计算公式,以容量为系统的状态变量,建立的空间模型如下:

式中:1,1分别表示过程噪声和观测噪声。
2) 以电池内阻为评价指标定义

根据电池的欧姆内阻定义的SOH计算公式,以内阻为系统的状态变量,建立的空间模型如下:

式中:2,2分别为过程噪声和观测噪声。
本文在同一个工况实验下,通过AUKF算法估计锂离子电池的容量与内阻结果如下图所示,将估算得到的容量与欧姆内阻代入式(18)和式(20)中,即可计算出电池的SOH。图11为电池的容量估计曲线,图12为电池的内阻变化曲线。

图11 电池容量估算曲线

图12 欧姆内阻估计值
由图12可知,利用AUKF算法估算电池的容量和内阻结果较好,欧姆内阻0估计值与参考值吻合度较高,即该估算算法精度较高,有较好的鲁 棒性。
5 结论
1) 以城市轨道交通为背景,研究复合动力储能系统储能元件的健康状态。首先根据城轨交通车辆复合储能系统蓄电池的特点,选取二阶RC等效电路模型为蓄电池模型。利用FFRLS辨识模型的参数,并基于MATLAB平台搭建蓄电池的SIMULINK模型,通过1.5 A的恒流模式下充电及2 A电流下的放电实验,验证了该模型的可靠性。
2) 基于建立的二阶RC等效电路模型,应用AUKF算法,不仅可以估算出电池的SOC还可以同时估算容量和欧姆内阻,并根据估算得出的容量和内阻值,实时估算电池的SOH。此外在1.5 A的恒流模式下进行充电及恒电流为2 A的水平下进行放电,直到锂离子电池的电压降至2.7 V的实验工况下,通过仿真对比分析可知,UKF算法和AUKF算法估计电池的SOC和SOH可行并都有一定的优越性,但AUKF算法相比于UKF算法,其优势在于精度较高,更具有实时性,在车辆运用上有很好的实用性。
[1] 胡婧娴, 林仕立, 宋文吉, 等. 城市轨道交通储能系统及其应用发展[J]. 储能科学与技术, 2014, 3(2): 106- 116. HU Jingxian, LIN Shili, SONG Wenji, et al. Energy storage for urban rail transportation[J]. Energy Storage Science and Technology, 2014, 3(2): 106-116.
[2] 季炳成. 超级电容器及其复合储能系统荷电状态研究[D]. 大连: 大连理工大学, 2015. JI Bingcheng. The research on graphene super capacitor and state-of-charge estimation of hybrid energy storage system[D]. Dalian: Dalian University of Technology, 2015.
[3] 郭亮, 贾彦, 康丽, 等. 一种蓄电池和超级电容器复合储能系统[J]. 储能科学与技术, 2017, 6(2): 297-301. GUO Liang, JIA Yan, KANG Li, et al. The composite storage using lead storage battery and EDLC[J]. Energy Storage Science and Technology, 2017, 6(2): 297-301.
[4] Ng K S, Moo C S, CHEN Y P, et al. Enhanced coulomb counting method for estimating state-of-charge and state- of-health of lithium-ion batteries[J]. Applied Energy, 2009, 86(9): 1506-1511.
[5] Meissner E, Richter G. The challenge to the automotive battery industry: The battery has to become an increasingly integrated component within the vehicle electric power system[J]. Journal of Power Sources, 2005, 144(2): 438-460.
[6] Kong Song-Ng, Moo Chin-Sien, CHEN Yiping, et al. Enhanced coulomb counting method for estimating state- of-charge and state-of-health of lithium-ion batteries[J]. Applied Energy, 2009, 86(9): 1506-1511.
[7] XIA Bizhong, LAO Zizhou, ZHANG Ruifeng, et al. State-of-charge estimation for lithium-ion batteries based on a nonlinear fractional mode[J]. IEEE Transactions on Control System Technology, 2016, 25(1): 3-11.
[8] 田强. 基于模型的纯电动汽车动力电池SOC估计方法研究[D]. 长沙: 湖南大学, 2018. TIAN Qiang. Study on SOC estimation method of power battery for electric vehicle based on model[D]. Changsha: Hunan University, 2018.
[9] 李金东, 古月圆, 王路阳, 等. 退役锂离子电池健康状态评估方法综述[J]. 储能科学与技术, 2019, 8(5): 807-811. LI Jindong, GU Yueyuan, WANG Luyang, et al. Review on state of health estimation of retired lithium-ion batteries[J]. Energy Storage Science and Technology, 2019, 8(5): 807-811.
[10] 张利, 张庆, 常成, 等. 用于电动汽车SOC估计的等效电路模型研究[J]. 电子测量与仪器学报, 2014, 28(10): 1161-1168. ZHANG Li, ZHANG Qing, CHANG Cheng, et al. Research on equivalent circuit model for state of charge estimation of electric vehicle[J]. Journal of Electronic Measurement and Instrumentation, 2014, 28(10): 1161- 1168.
[11] 安治国, 田茂飞, 赵琳, 等. 基于自适应无迹卡尔曼滤波的锂电池SOC估计[J]. 储能科学与技术, 2019, 8(5): 856-861. AN Zhiguo, TIAN Maofei, ZHAO Lin, et al. SOC estimation of lithium based on adaptive untracked Kalman filter[J]. Energy Storage Science and Technology, 2019, 8(5): 856-861.
[12] Remmlinger J, Buchholz M, Meiler M. State-of-health monitoring of lihium-ion batteries in electric vehicles by on-board internal resistance estimation[J]. Journal of Power Sources, 2011, 196: 5357-5363.
[13] 曹夏令, 费亚龙, 孙绍博, 等. 基于自适应无迹卡尔曼滤波器的锂电池SOC估计[J]. 电力电子技术, 2017, 51(7): 69-72. CAO Xialing, FEI Yalong, SUN Shaobo, et al. SOC estimation of lithium battery based on AUKF[J]. Power Electronics, 2017, 51(7): 69-72.
[14] 张绍虹. 电动汽车锂离子电池SOH估算方法研究[D]. 太原: 太原理工大学, 2019. ZHANG Shaohong. Research on SOH estimation method for lithium-ion battery electric vehicle[D]. Taiyuan: Taiyuan University of Technology, 2019.
[15] 颜湘武, 邓浩然, 郭琪, 等. 基于自适应无迹卡尔曼滤波的动力电池健康状态检测及梯次利用研究[J]. 电工技术学报, 2019, 34(18): 3937-3947. YAN Xiangwu, DENG Haoran, GUO Qi, et al. Study on the state of health detection of power batteries based on adaptive unscented Kalman filters and the battery echelon utilization[J]. Transactions of China Electro Technical Society, 2019, 34(18): 3937-3947.
[16] 曾文文. 锂离子电池健康状态评估及剩余寿命预测方法[D]. 淮南: 安徽理工大学, 2019. ZENG Wenwen. State-of-health estimation and remaining useful life prediction method of lithium-ion battery[D]. Huainan: Anhui University of Science and Technology, 2019.
[17] 刘大同, 周建宝, 郭力萌, 等. 锂离子电池健康评估和寿命预测综述[J]. 仪器仪表学报, 2015, 36(1): 1-16. LIU Datong, ZHOU Jianbao, GUO Limeng, et al. Survey on lithium-ion battery health assessment and cycle life estimation[J]. Chinese Journal of Scientific Instrument, 2015, 36(1): 1-16.
Estimation of battery SOC and SOH for urban rail vehicle composite power energy storage system
GUO Youmin1, 2, 3, DAI Yinjuan1, 2, 3, FU Shilei1, 2, 3
(1. Mechatronics T&R Institute, Lanzhou Jiaotong University, Lanzhou 730070, China;2. Gansu Provincial Engineering Technology Center for Informatization of Logistics & Transport Equipment, Lanzhou 730070, China;3. Gansu Provincial Industry Technology Center of Logistics & Transport Equipment, Lanzhou 730070, China)
The purpose of this paper is to estimate the state of charge (SOC) and state of health (SOH) of the battery of the urban rail transit composite energy storage system. This paper adopted a second-order RC equivalent circuit model that meets the operating conditions of urban rail transit vehicles and identifies its model parameters by the forgetting factor least square algorithm. Based on the second-order RC equivalent circuit model, the traditional adaptive unscented Kalman filter algorithm was used to estimate the state of charge (SOC) of the battery. Due to the complex running environment of the train, the noise of the battery was a dynamic change value. The error of the estimation result is large, and the maximum error is 5.5%. Therefore, this paper used the adaptive unscented Kalman filter algorithm (AUKF) to estimate the state of charge (SOC), Ohmic internal resistance and capacity of the battery in real time. According to the relationship between the Ohmic internal resistance, capacity and battery SOH, the battery’s SOH was estimated. Finally, the experimental results show that compared with UKF algorithm, AUKF algorithm can estimate SOC and model parameters in real-time cycle at the same time. According to the observation value, it can update the noise automatically. Therefore, it has better practicability and higher accuracy for the actual operation of the train, with the maximum error of 3.5% and the average error of 1.5%.
battery; state of charge; state of health; second order RC equivalent circuit model; adaptive unscented Kalman filter
U223.6
A
1672 - 7029(2020)11 - 2920 - 09
10.19713/j.cnki.43-1423/u.T20200047
2020-01-13
国家重点研发计划资助项目(2017YFB1201003-20);甘肃省高等学校科研资助项目(2018C-10)
郭佑民(1968-),男,甘肃陇西人,教授,从事设备控制与监测等方向研究;E-mail:18209317506@163.com

(编辑 阳丽霞)
