基于改进观测方程的非线性恢复力免模型识别方法

齐梦晨，张肖雄，贺佳

基于改进观测方程的非线性恢复力免模型识别方法

齐梦晨，张肖雄，贺佳

(湖南大学 土木工程学院 风工程与桥梁工程湖南省重点实验室，湖南 长沙 410082)

现有的非线性恢复力参数化识别方法需已知非线性模型，并明确模型中参数的物理意义，而非参数化方法(如基于各类多项式的识别方法)往往难以准确识别突变处的恢复力。为进一步改进方法，提出一种非线性恢复力免模型识别法。该方法利用改进的观测方程，将非线性恢复力视作虚拟外激励，无需对非线性恢复力做参数化或非参数化模型假设，利用最小二乘和扩展卡尔曼滤波原理，同步识别结构参数和非线性恢复力，并且通过多次整体迭代保证识别结果稳定收敛。以含有Bingham模型和分段线性系统的5层框架数值模型为例，验证了该方法的有效性，并将其识别结果与基于切比雪夫多项式模型的非参数化识别方法进行对比，体现了该方法在识别恢复力非平滑处的优越性。

非线性恢复力；全局迭代；扩展卡尔曼滤波；虚拟外激励；免模型识别；

土木结构受某些因素影响，例如强动力荷载、疲劳累积、环境腐蚀等，易产生不同程度的损伤，从而影响结构安全、缩短使用寿命，甚至产生破坏，给人民生命财产造成损失。因此，有效识别结构损伤、评估结构健康状况显得十分重要。基于结构动力响应信息，识别结构参数变化，进而判断结构损伤程度是目前损伤识别常用方法之一[1-2]。然而，在动力荷载作用下，结构损伤的发生、发展过程往往具有非线性特征，基于结构模态信息或特征值提取的损伤识别方法将不再适用，因此，发展适合非线性系统的损伤识别方法具有重要意义。非线性恢复力(Nonlinear Restoring Force, NRF)往往与结构速度或位移有关，不仅可以表征结构非线性发生发展的过程，还可以定量评估结构在振动过程中耗能特性，因此，研究结构非线性恢复力识别方法对非线性结构损伤识别具有重要的理论和现实意义。目前，非线性恢复力的识别方法基本可分为参数化识别和非参数化识别。参数化识别方法以非线性恢复力模型为基础，并往往要求模型参数具有物理意义。非线性模型众多，因此，针对不同的对象、不同的研究目标，有不同的参数化识别方法。由于篇幅限制和研究相关性，本文仅给出了近年来发展的基于扩展卡尔曼滤波(Extended Kalman Filter, EKF)的一些非线性参数化识别方法。基于EKF算法，LEI等[3]提出了部分观测信息下的非线性参数识别方法，并通过Bouc-Wen模型数值算例验证了方法的有效性。利用直接微分方法，Ebrahimian 等[4]提出了基于EKF的非线性模型修正方法。通过依次采用EKF和无迹卡尔曼滤波(Unscented Kalman Filter, UKF)，LIU等[5]提出了非线性系统参数的分步识别方法。针对非线性时变系统，XIAO等[6]提出了基于EKF的自适应识别法。为考虑模型非确定性，Astroza等[7-8]提出了基于自适应非线性模型修正方法，并与基于卡尔曼滤波(Kalman Filter, KF)的模型修正方法进行了比较。以上各种基于EKF的非线性识别方法，在有效识别了非线性参数后，均能计算得到结构的非线性恢复力。然而，一旦非线性模型不确定，以上方法就不再适用，因此，不少学者开展了非参数化识别方法的研究。类似的，这里仅给出了基于EKF的一些非参数化识别方法。XU等[9-10]提出了基于双重切比雪夫多项式的非线性恢复力识别方法，并通过安装有形状记忆合金阻尼器的钢框架模型实验验证了方法的可行性。LIU等[11]将非线性系统等效线性化后，采用EKF对非线性进行定位，进而基于UKF识别该用幂级数多项式描述的非线性恢复力。利用幂级数多项式表征NRF，LEI等[12-13]提出了基于等价线性理论和EKF的非线性识别方法。ZHANG等[14]将非线性恢复力线性化，根据响应重构识别弱非线性框架的刚度和阻尼。SU等[15]提出两步非线性恢复力识别法，在结构非线性行为较弱时，将非线性系统等效成线性系统，基于EKF原理识别结构参数后，再将非线性恢复力视作“未知外激励”采用KF-UI(Kalman Filter with unknown input)算法进行识别。利用线性结构参数，李靖等[16]提出了基于等价线性原理和UKF的NRF免参数识别方法。同样利用线性结构参数，雷鹰等[17]借助EKF和最小二乘(Least Squares Estimation, LSE)对结构橡胶支座非线性部分免参数识别。许斌等[18-19]还提出基于切比雪夫多项式和幂级多项式的EKF免参数识别方法。以上基于各类多项式的非参数识别方法均能有效识别结构的非线性特征，然而，在某种程度上，这些方法仍依赖于选取的非参数化模型的合理性和有效性，同时，由于多项式模型的本身的特性，在非线性恢复力非平滑处往往难以实现可靠识别。本文提出一种基于改进观测方程的非线性恢复力免模型识别方法，该方法将非线性恢复力视为“虚拟外激励”，利用投影矩阵，获得了一种不显式包含该“虚拟外激励”的观测方程，基于LSE和EKF原理，实现了结构状态的递推估计和非线性恢复力的同步识别。此外，为确保识别结果稳定收敛，该方法在一次迭代过程结束时，将递推估计的结构参数最终识别值作为下一个迭代的初始值，重复上述过程，直至满足收敛条件。

1 理论推导

一般的，非线性结构的运动平衡方程可写成：

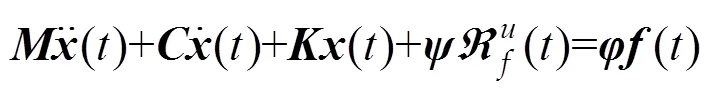
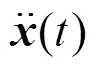
将非线性恢复力视作“虚拟外激励”，则式(1)可写成，

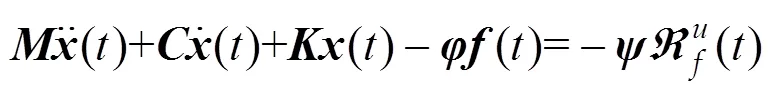
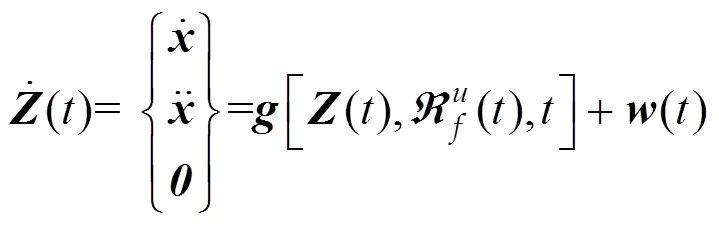
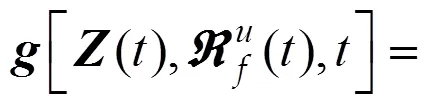
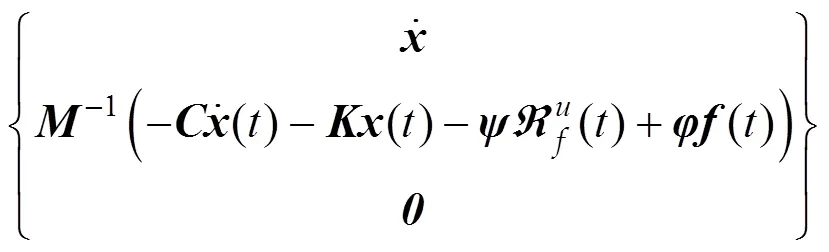
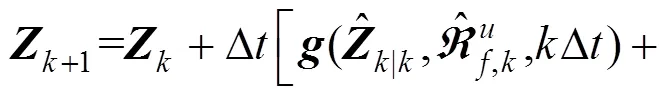
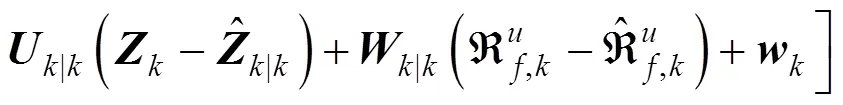
其中

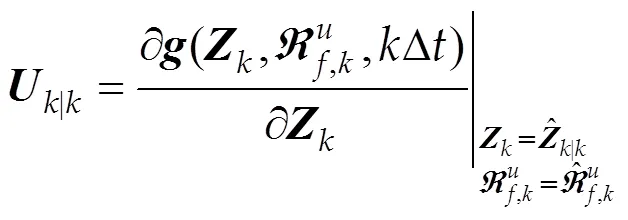
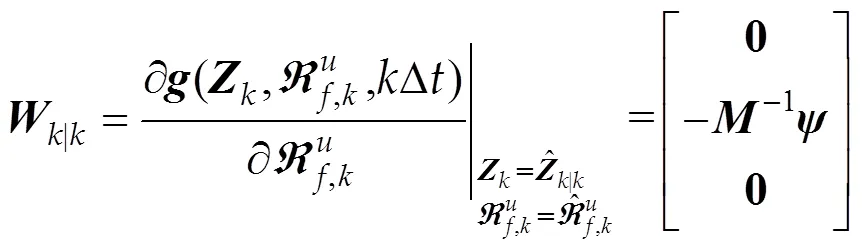
文中假设观测了部分加速度响应，则离散化的观测方程为：

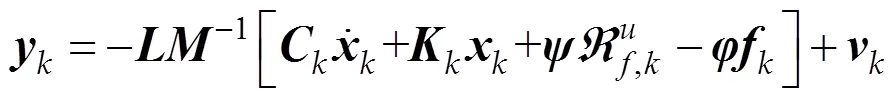
式中：为第步的加速度响应观测值；为位置观测矩阵；为均值为0；协方差为的观测噪声。

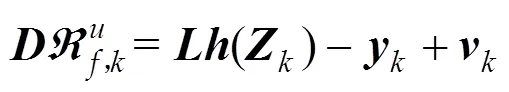
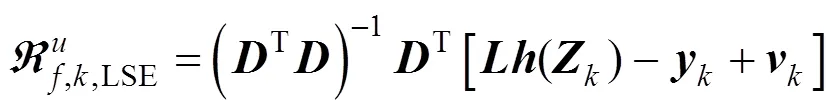
式(7)和式(8)之间的估计误差可写成：

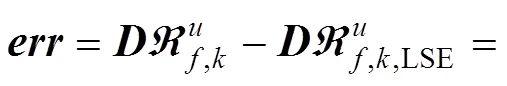
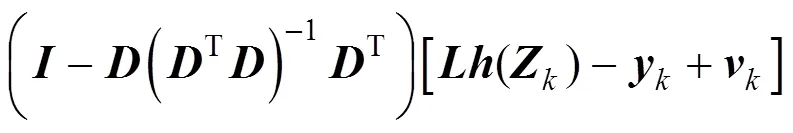
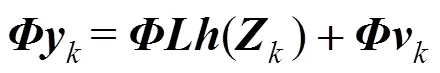
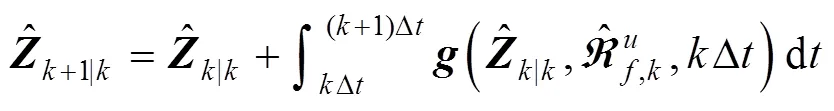
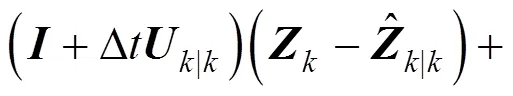
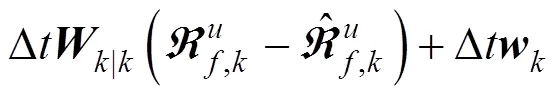
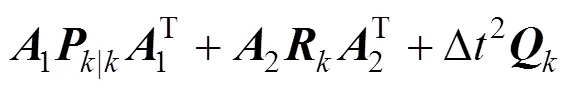
其中

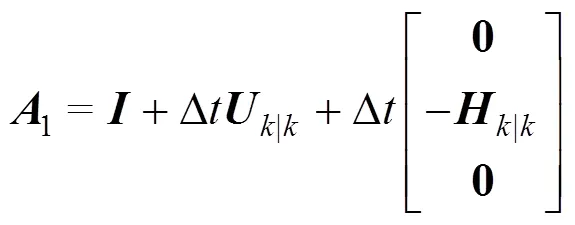
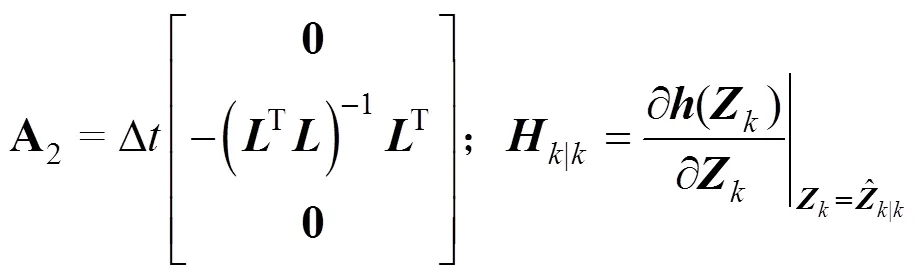
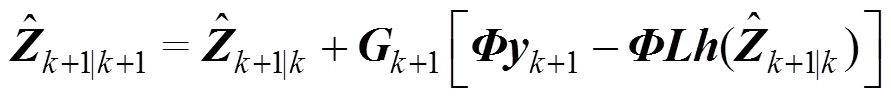
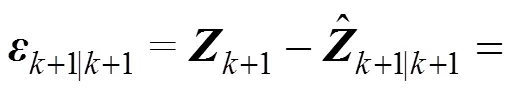
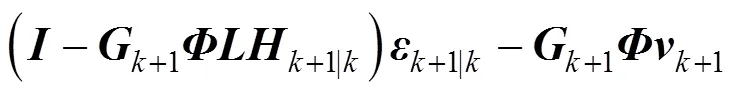
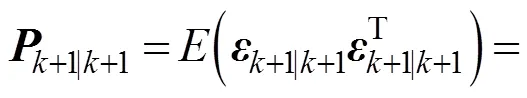
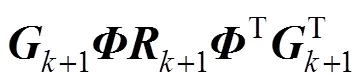
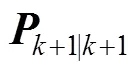
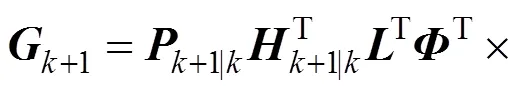
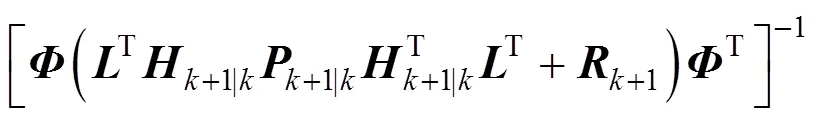
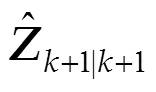
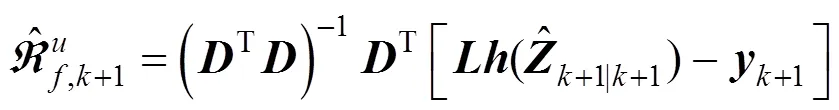
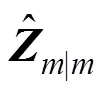
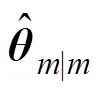
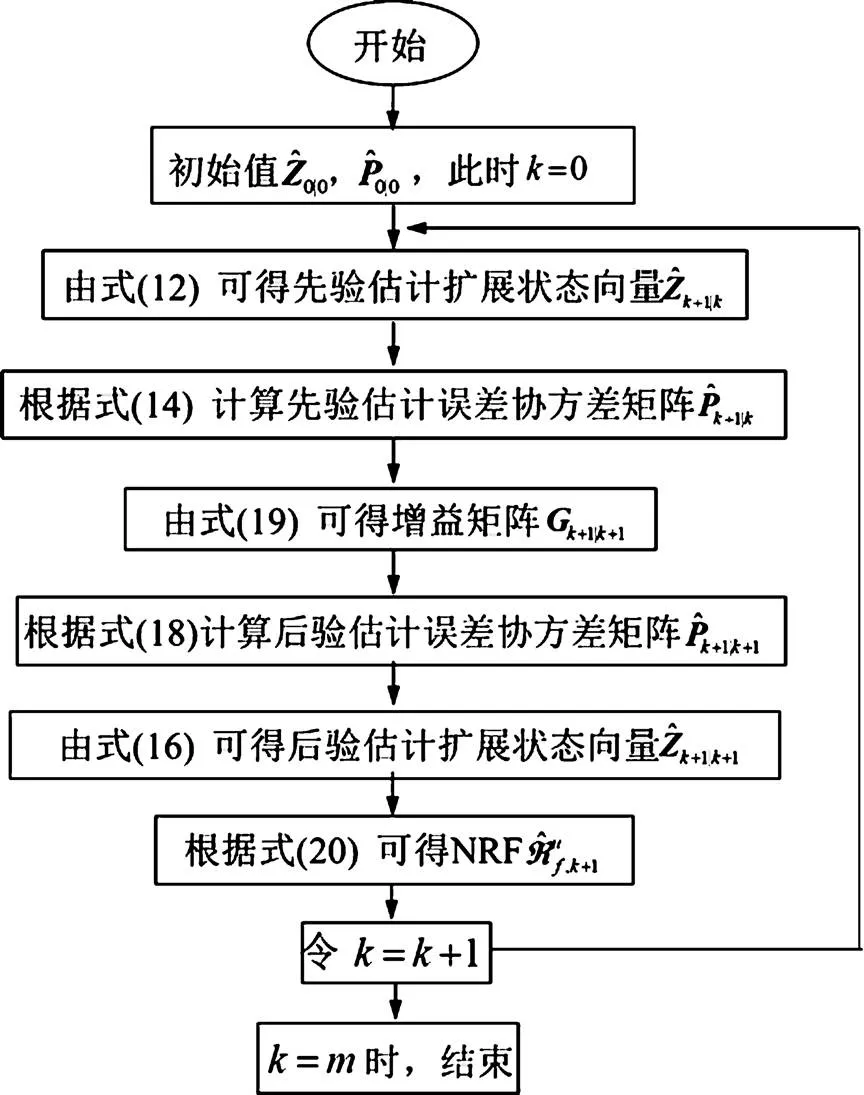
图1 基于EKF的非线性恢复力免模型识别流程图

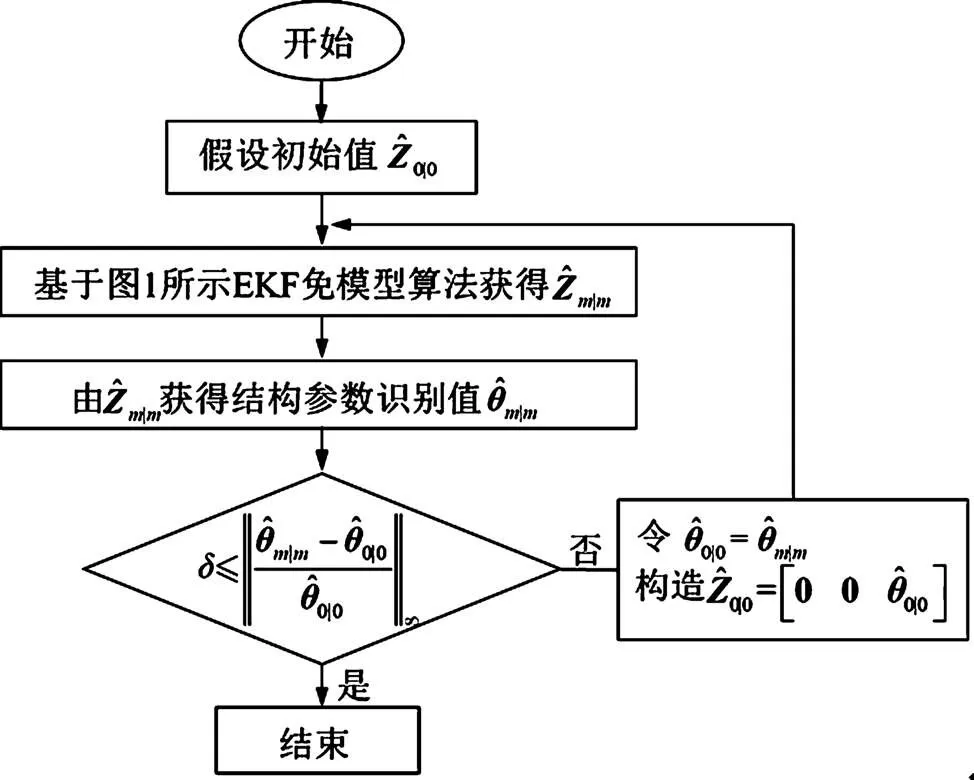
图2 基于EKF的全局迭代流程图

2 数值算例

为了验证算法的有效性，对图3所示的含有非线性构件的5层框架结构在2种工况下的非线性恢复力进行了免模型识别。结构参数设为m=500 kg，k=1.5×105N/m。这里，考虑底层分别存在2种不同的非线性模型，即Bingham模型和分段线性模型。此外，为考察外激励位置和形式对识别结果的影响，分别考虑了2种荷载工况，即作用于结构第2层的随机激励和作用于基底的地震荷载。

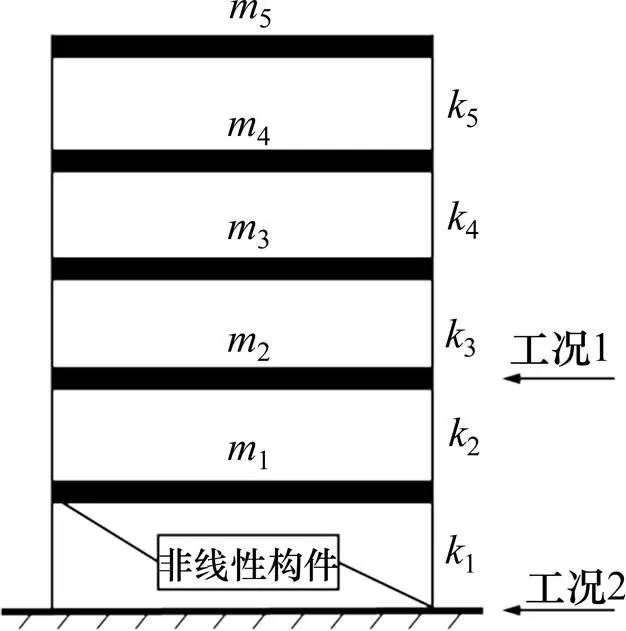
图3 数值模型

2.1 工况1：Bingham模型

在工况1中，假设随机外激励作用于结构第2层，非线性构件的力学行为由Bingham模型描述，其数学表达式为

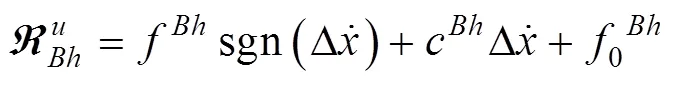
其中：为层间速度，均为Bingham模型参数，这里取，，=0 N。外激励作用时间为3 s，如图4所示。

此工况中，结构阻尼采用瑞利阻尼模型，阻尼系数取值=0.220 3；=0.003 1。结构响应由龙格库塔法计算得出，计算时间步长为0.001 s。由于实际情况中，实测信号不可避免地存在噪声，故在观测信号中引入5%的噪声。取结构第1，2，3和5层的加速度响应作为观测量，假设结构参数初始值为真实值的50%。并且假定当<0.00 5时，迭代过程结束。

计算过程在迭代4次后结束，结构参数最终识别结果及相对误差如表1所示。可以看出，最大误差只有-1.04%，识别结果相对准确。图5进一步给出了第1次迭代和最后一次迭代的参数识别结果，受篇幅限制，这里仅给出了第一层的刚度1以及阻尼系数的识别结果。由图中不难看出，在第1次迭代中，虽然刚度识别结果较好，但是阻尼系数并未稳定收敛；在最后一次迭代中，刚度和阻尼系数在整个递推过程中均稳定收敛于真实值附近。图6为识别的NRF，可以看出识别值与真实值吻合 较好。

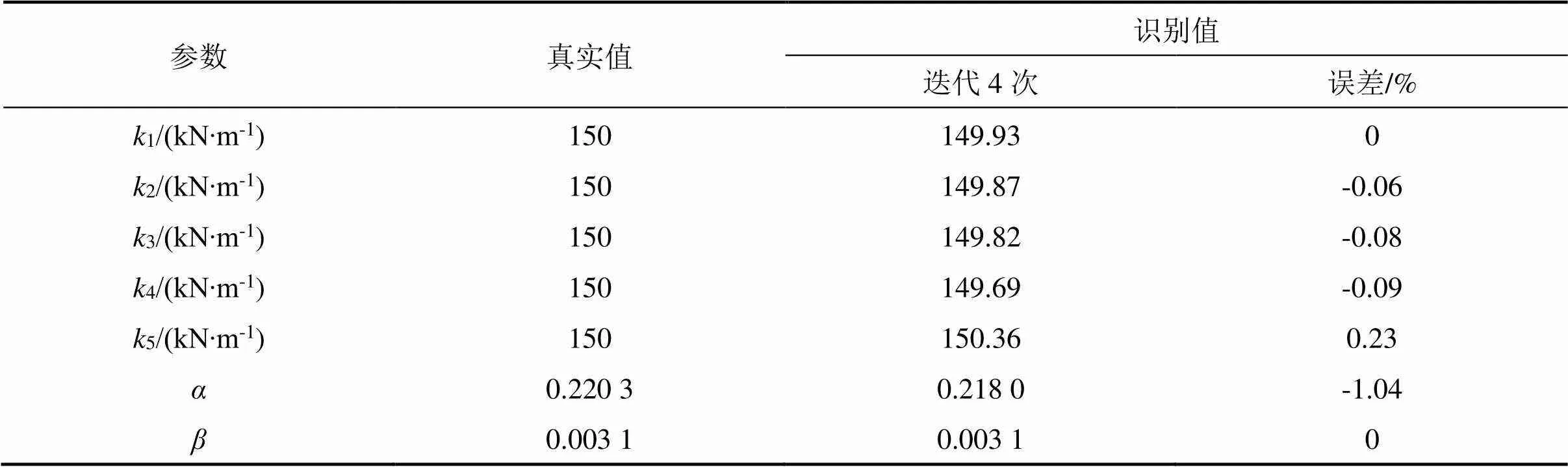
表1 结构参数识别结果

2.2 工况2：分段线性模型

工况2假设以峰值加速度为3.4的El Centro地震波作用于该结构，底层的非线性模型采用分段线性模型，如图7所示，其表达式如下：

(a)1(第1次迭代)；(b)1(第4次迭代)；(c)(第1次迭代)；(d)(第4次迭代)

图5 参数识别结果

Fig. 5 Identified structural parameters

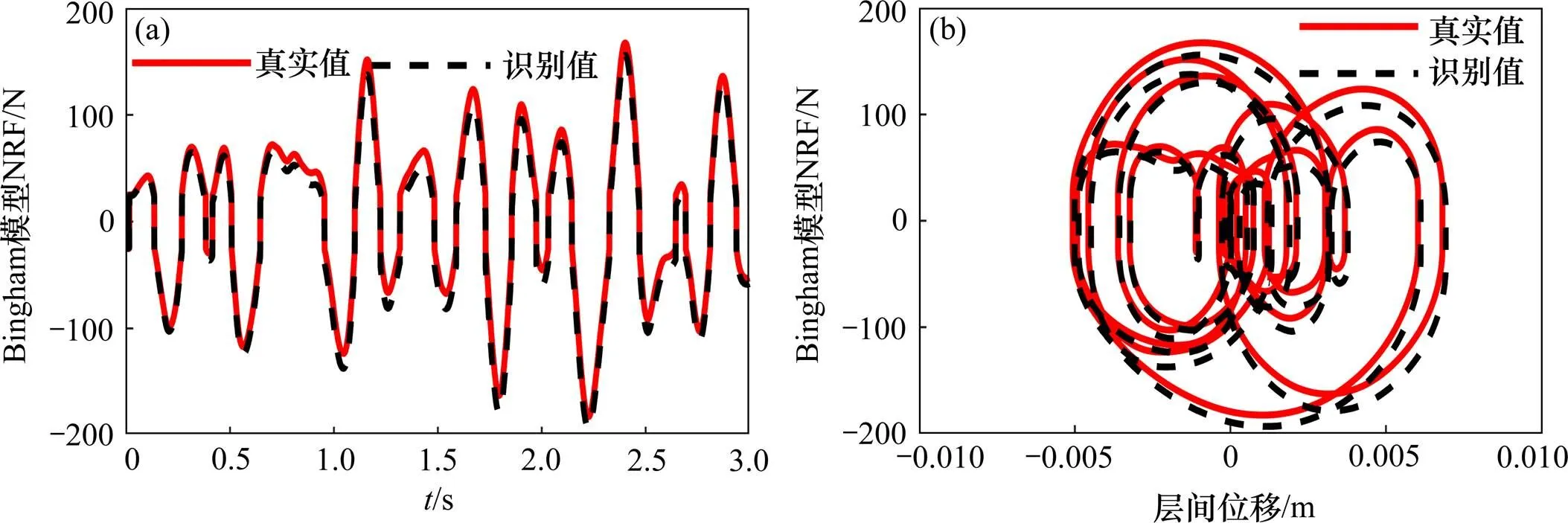
(a) 时程曲线；(b) 滞回曲线

为考察阻尼的影响，该工况中结构采用黏滞阻尼模型，取值为c=350 (N∙s)/m，(=1,2,…,5)。结构非线性时程响应同样由龙格库塔法求得，计算步长设为0.001 s。假设结构第1，2，3和5层的加速度响应为观测量，考虑5%的噪声影响。结构参数初始值取为结构参数真实值的30%，同样假定当<0.005时，迭代过程结束。

识别过程在迭代3次后结束，最终识别结果及相对误差如表2所示，从表2中不难看出，最大识别误差为-2.62%，识别结果可靠。为进一步了解计算过程中参数收敛情况，图8给出了第1次和最后一次迭代过程中的结构刚度和阻尼系数的识别情况，由于篇幅限制，仅给出了第4层(未观测加速度层)的结构参数识别过程。从图8中同样可以看出，在第1次迭代过程中，虽然结构刚度参数收敛得较好，但是阻尼系数不能稳定收敛；在最后一次迭代中，刚度和阻尼参数均稳定收敛于真实值。

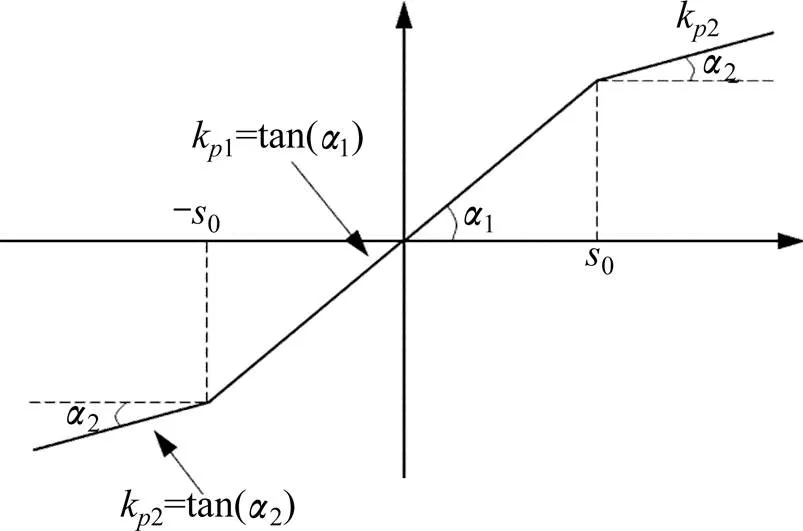
图7 分段线性模型

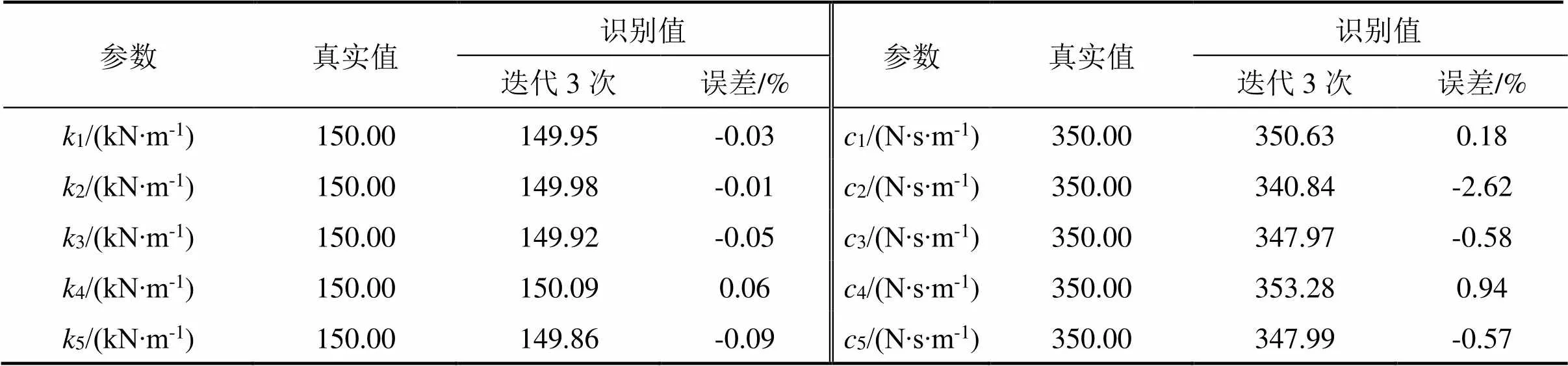
表2 结构参数识别结果

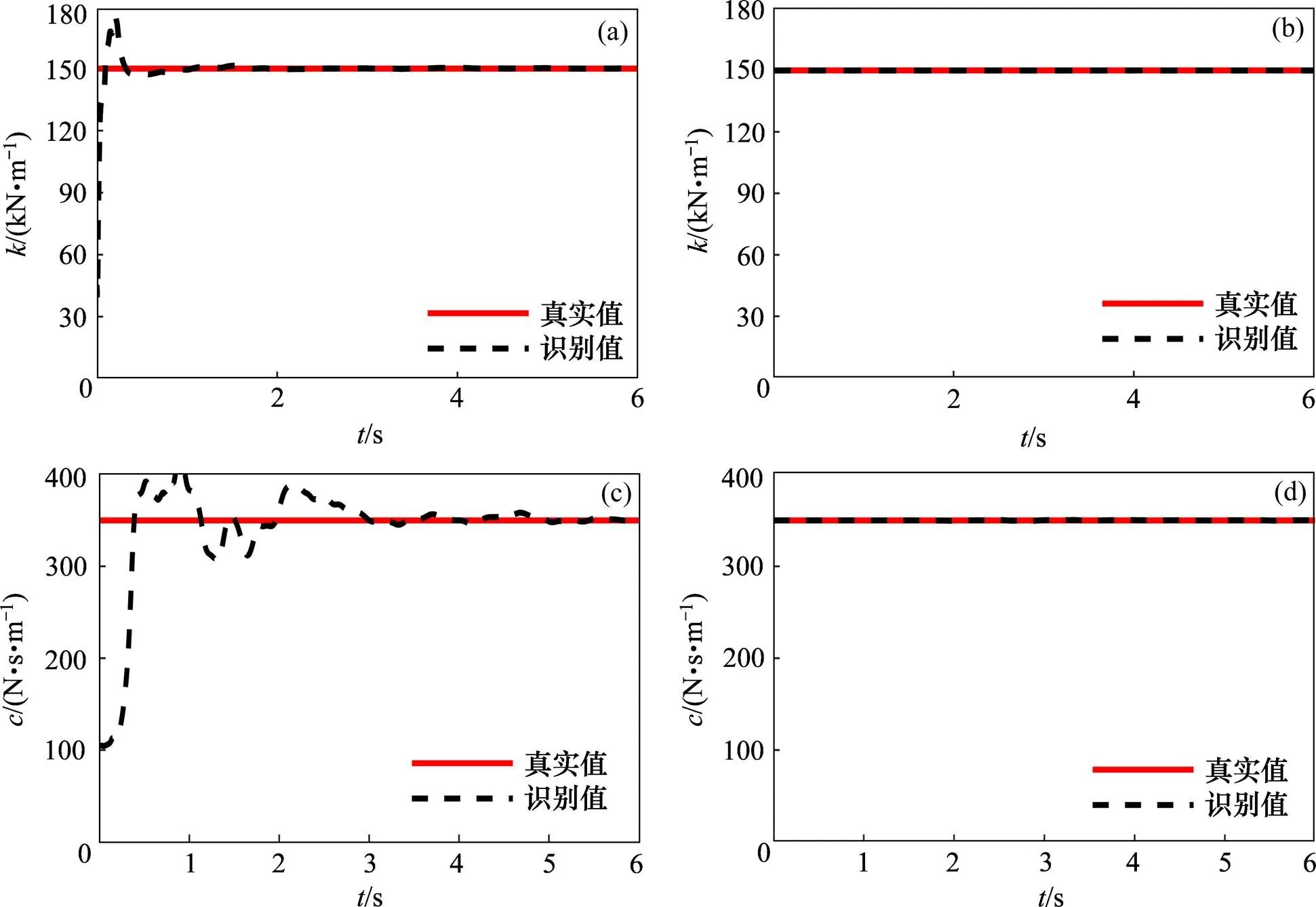
(a) k4(第1次迭代)；(b) k4(第3次迭代)；(c) c4(第1次迭代)；(d) c4(第3次迭代)

为了表明算法在识别恢复力非平滑点处的优越性，这里也采用基于高阶切比雪夫多项式(待识别系数高达25个)的非参数化方法识别了结构的NRF。图9(a)比较了2种方法的识别结果，从图中可以看出，本文方法的NRF识别值与真实值吻合更好，尤其在刚度突变处。为便于比较，图9(b)给出了2种结果识别误差的时程曲线，从图中不难看出，本文提出的方法的识别误差普遍低于基于切比雪夫多项式的非参数化方法的识别误差。为进一步对比分析，以层间位移为横坐标，图9(c)给出了2种方法的误差对比，图9中点画线表示临界相对位移，即刚度突变处，从图9(c)可以看出，在刚度突变点处本文方法的识别误差明显小于基于切比雪夫多项式识别的误差。

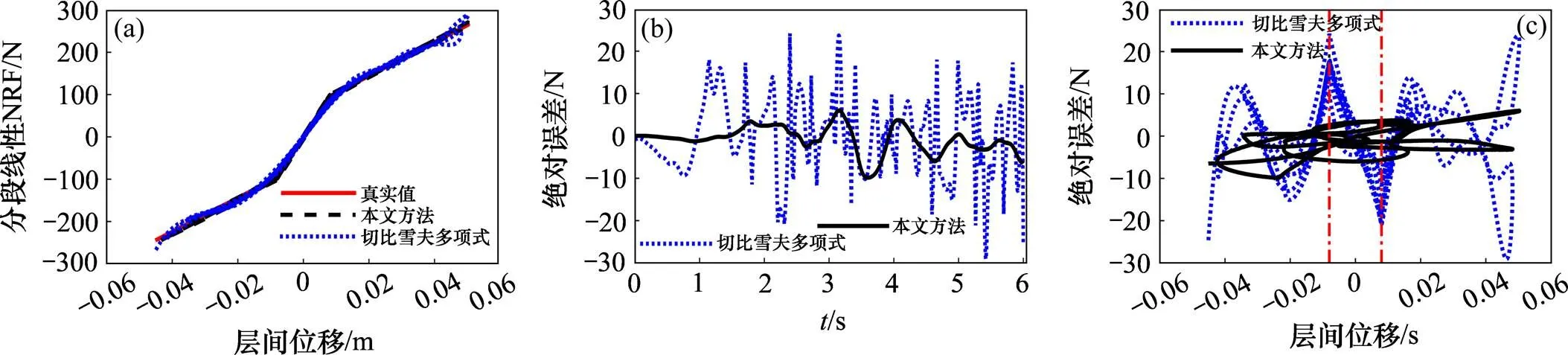
(a) 识别值与真实值比较；(b) 误差比较(时间为横坐标)；(c) 误差比较(相对位移为横坐标)

3 结论

1) 提出一种基于改进观测方程的非线性恢复力免模型识别方法，该方法将NRF视作虚拟外激励，因而，无需提前对其做参数化或非参数模型 假设。

2) 利用投影矩阵，获得了改进的观测方程，并基于LSE和EKF原理，同步识别了结构相关参数和对应的NRF的时程信息，并通过经过多次整体迭代，有效保证了识别结果稳定收敛。

3) 文中通过一个安装有Bingham模型和分段线性模型的5层框架数值模型验证了该方法的可行性，并与基于高阶切比雪夫多项式的NRF识别方法进行对比，发现本文提出的方法能更有效地识别刚度突变处的恢复力大小。

[1] LI Jun, HAO Hong. A review of recent research advances on structural health monitoring in Western Australia[J]. Structural Monitoring and Maintenance, 2016, 3(1): 33- 49.

[2] XU Youlin, HE Jia. Smart civil structures[M]. Boca Raton: CRC Press, 2017: 333-389.

[3] LEI Ying, WU Yan, LI Tao. Identification of nonlinear structural parameters under limited input and output measurements[J]. International Journal of Non-Linear Mechanics, 2012, 47(10): 1141–1146.

[4] Ebrahimian H, Astroza R, Conte J P. Extended Kalman filter for material parameter estimation in nonlinear structural finite element models using direct differentiation method[J]. Earthquake Engineering & Structural Dynamics, 2015, 44(10): 1495-1522.

[5] LIU Lijun, LEI Ying, HE Mingyu. A two-stage parametric identification of strong nonlinear structural systems with incomplete response measurements[J]. International Journal of Structural Stability and Dynamics, 2016(16): 1640022

[6] XIAO Mengli, ZHANG Yongbo, WANG Zhihua. An adaptive three-stage extended Kalman filter for nonlinear discrete-time system in presence of unknown inputs[J]. ISA Transactions, 2018(75): 101-117.

[7] Astroza R, Alessandri A, Conte J P. A dual adaptive filtering approach for nonlinear finite element model updating accounting for modeling uncertainty[J]. Mechanical Systems and Signal Processing, 2019(115): 782-800.

[8] Astroza R, Ebrahimian H, Conte J P. Performance comparison of Kalman-based filters for nonlinear structural finite element model updating[J]. Journal of Sound Vibration, 2019(438): 520-542.

[9] XU Bin, HE Jia, DYKE S J. Model-free nonlinear restoring force identification for SMA dampers with double Chebyshev polynomials: Approach and validation [J]. Nonlinear Dynamics, 2015, 82(3): 1507-1522.

[10] Xu Bin, He Jia, Masri S F. Data-based model-free hysteretic restoring force and mass identification for dynamic systems[J]. Computer-Aided Civil and Infrastructure Engineering, 2015, 30(1): 2-18.

[11] Liu Lijun, Lei Ying, He Mingyu. Locating and identifying model-free structural nonlinearities and systems using incomplete measured structural responses [J]. Smart Structures and Systems, 2015, 15(2): 409-424.

[12] Lei Ying, Hua Wei, Luo Sujuan, et al. Detection and parametric identification of structural nonlinear restoring forces from partial measurements of structural responses [J]. Structural Engineering and Mechanics, 2015, 54(2): 291-304.

[13] Lei Ying, Luo Sujuan, He Mingyu. Identification of model-free structural nonlinear restoring forces using partial measurements of structural responses[J]. Advances in Structural Engineering, 2017, 20(1): 69-80.

[14] Zhang Genbei, Zang Chaoping, Friswell M I. Identification of weak nonlinearities in MDOF systems based on reconstructed constant response tests [J]. Archive of Applied Mechanics, 2019, 89(10): 2053- 2074.

[15] Su Han, Yang Xiongjun, Liu Lijun, et al. Identifying nonlinear characteristics of model-free MR dampers in structures with partial response data[J]. Measurement, 2018, 130: 362-371.

[16] 李靖, 许斌. 部分观测下结构质量及非线性恢复力免模型识别[J]. 噪声与振动控制, 2019, 39(1): 160-165. LI Jing, XU Bin. Identification of structural mass and model free nonlinear restoring forces with partial measurements[J]. Noise and Vibration Control, 2019, 39(1): 160-165.

[17] 雷鹰, 何明煜, 林树枝. 结构中基底橡胶隔震支座非线性特性的无模型识别[J]. 振动与冲击, 2013, 32(20): 1-4. LEI Ying, HE Mingyu, LIN Shuzhi. Model free identification of nonlinear properties of rubber-bearings in base-isolated buildings[J]. Journal of Vibration and Shock, 2013, 32(20): 1-4.

[18] 许斌, 王云. 利用部分加速度测量的结构滞回特性免模型识别[J]. 工程力学, 2018, 35(2): 180-187. XU Bin, WANG Yun. Model free structural hysteritic behavior identification with limited acceleration measurements[J]. Engineering Mechanics, 2018, 35(2): 180-187.

[19] 许斌, 辛璐璐, 贺佳. 基于切比雪夫多项式模型的多自由度结构非线性恢复力时域识别[J]. 工程力学, 2014, 31(11): 99-109. XU Bin, XIN Lulu, HE Jia. Time domain nonlinear- restoring force identification for MD of structures with chebyshev polynomial model[J]. Engineering Mechanics, 2014, 31(11): 99-109.

Identification of nonlinear restoring force in a model-free manner based on revised observation equation

QI Mengchen, ZHANG Xiaoxiong, HE Jia

(Key Laboratory of Wind and Bridge Engineering of Hunan Province, College of Civil Engineering, Hunan University, Changsha 410082, China)

The existing parametric approaches for the identification of nonlinear restoring force (NRF) basically require their deterministic NRF models and have to clarify the physical meaning of each parameter. For many nonparametric techniques, their nonparametric models or approximations may result in undesirable results or oscillations around unsmooth points. Therefore, based on the revised observation equation, a model-free NRF identification approach was proposed in this study. The NRF to be identified was treated as “unknown fictitious input”, and thus the prior knowledge of the expression of NRF was not required. The revised observation equation, where the unknown NRF was implicitly involved, was employed. Based on the principle of least squares estimation (LSE) and extended Kalman filter (EKF), the formulas of the proposed approach for the identification of NRF were then derived. The structural parameters and the NRF could be simultaneously identified. A global iteration procedure was employed to assure the convergence of the identification results. The effectiveness of the proposed approach is numerically verified via a five-story building equipped with Bingham model and piecewise linear model. As compared with the nonparametric identification method using Chebyshev polynomial model, the superiority of the proposed method in identifying the non-smoothness of NRF is demonstrated.

nonlinear restoring force; global iteration; extended Kalman filter; unknown fictitious input; model-free identification

TU3

A

1672 - 7029(2020)11 - 2729 - 09

10.19713/j.cnki.43-1423/u.T20200068

2020-01-20

国家自然科学基金资助项目(51708198)；湖南省自然科学基金资助项目(2018JJ3054)

贺佳(1983-)，男，湖南长沙人，副教授，博士，从事结构健康监测及系统识别研究；E-mail：jiahe@hnu.edu.cn

(编辑 蒋学东)