大跨度独塔斜拉桥斜拉索抗震性能研究

雷立本，夏修身，戴晓春，王晋博，韩森

大跨度独塔斜拉桥斜拉索抗震性能研究

雷立本1，夏修身1，戴晓春2，王晋博1，韩森1

(1. 兰州交通大学 土木工程学院，甘肃 兰州 730070；2. 中铁二院工程集团有限责任公司，四川 成都 610031)

为了研究斜拉索的抗震性能，以某大跨度独塔斜拉桥为工程背景，采用MIDAS CIVIL软件建立全桥有限元模型，分别按照顺桥向和横桥向2种方式输入不同强度的地震动。通过非线性时程分析方法分析斜拉索的地震反应，寻找最不利索梁锚固和最不利受力索的位置，考查最不利拉索位置随地震强度的变化规律。研究结果表明：与水平面夹角约33°的C7号拉索为最大拉力索，其为最不利锚固索；与水平面夹角约36°～38°区域的拉索为最大拉应力索，其为最不利受力索；顺桥向输入时拉索地震反应较横桥向输入时更不利。研究结果可供斜拉桥抗震设计时参考。

斜拉桥；斜拉索；地震响应；索梁锚固

我国地处亚欧板块与太平洋板块之间，地壳运动较活跃，近年来发生的强震均造成了大量桥梁不同程度的破坏，导致了巨大的经济损失，也对抗震救援工作造成了困难[1−2]。随着斜拉桥建设数量的日益增加，其面临强震的威胁也越来越大[3]。斜拉索作为斜拉桥的重要组成部分，其设计的合理性直接关系整个桥梁的安全[4]。1999年集集地震中，集鹿大桥发生斜拉索锚固失效的震害暴露出斜拉桥中斜拉索也是抗震薄弱部位[5]。因此，开展斜拉桥斜拉索抗震性能研究具有重要的意义。目前，国内外学者对斜拉索开展了诸多研究。宋涛等[6−8]开展了静力状态下的索力优化研究。REN等[9−11]研究了拉索在地震作用下的垂度问题。XIA等[12]采用数值方法研究了拉索在随机荷载下的参数振动问题。叶爱君等[13]研究了拉索局部振动对超大跨度斜拉桥地震响应的影响。易江等[14]研究发现强震下斜拉索会发生松弛现象。从已有的文献可以看出，对斜拉桥斜拉索抗震性能的研究较少，已有的研究没有涉及不同强度地震下最不利受力拉索及最不利索梁锚固位置的确定。本文以某大跨度独塔斜拉桥为工程背景，建立全桥有限元分析模型，输入不同强度的地震动，通过非线性时程分析方法分析了斜拉索的地震反应，寻找了最不利索梁锚固和最不利受力索的位置,探讨了不同输入方式对拉索地震反应的影响。

1 有限元模型建立

1.1 背景工程

某H型独塔双索面钢混结合梁斜拉桥，跨径布置为221 m+221 m，双向十车道，结构体系为半漂浮体系，主塔总高度为150 m、采用变截面形式，塔身设置两道变截面横梁，边墩为门架墩，采用钻孔桩基础，桥面宽度全宽为43 m，梁高3.5 m。结合梁混凝土板采用 C60 混凝土，主塔采用 C50 混凝土，边墩采用 C40 混凝土，承台采用C35混凝土，桩基采用C30混凝土，斜拉索采用f7镀锌高强钢丝。该桥总体布置图和桥塔立面图见图1。全桥采用平面双索面扇形形式对称布置72根斜拉索。为了方便分析，文中对梁端至塔身一侧的拉索按Ｃ1～Ｃ18进行编号，其中，C1及Ｃ4～Ｃ7号拉索横截面积约为0.013 0 m2，C2和C3号拉索横截面积约为0.013 4 m2，Ｃ8～Ｃ11号拉索横截面积约为0.010 9 m2，Ｃ12，Ｃ13及C18号拉索横截面积约为0.009 3 m2，C14号拉索横截面积约为0.008 1 m2，Ｃ15和C16号拉索横截面积约为0.007 6 m2，C17号拉索横截面积约为0.006 3 m2。

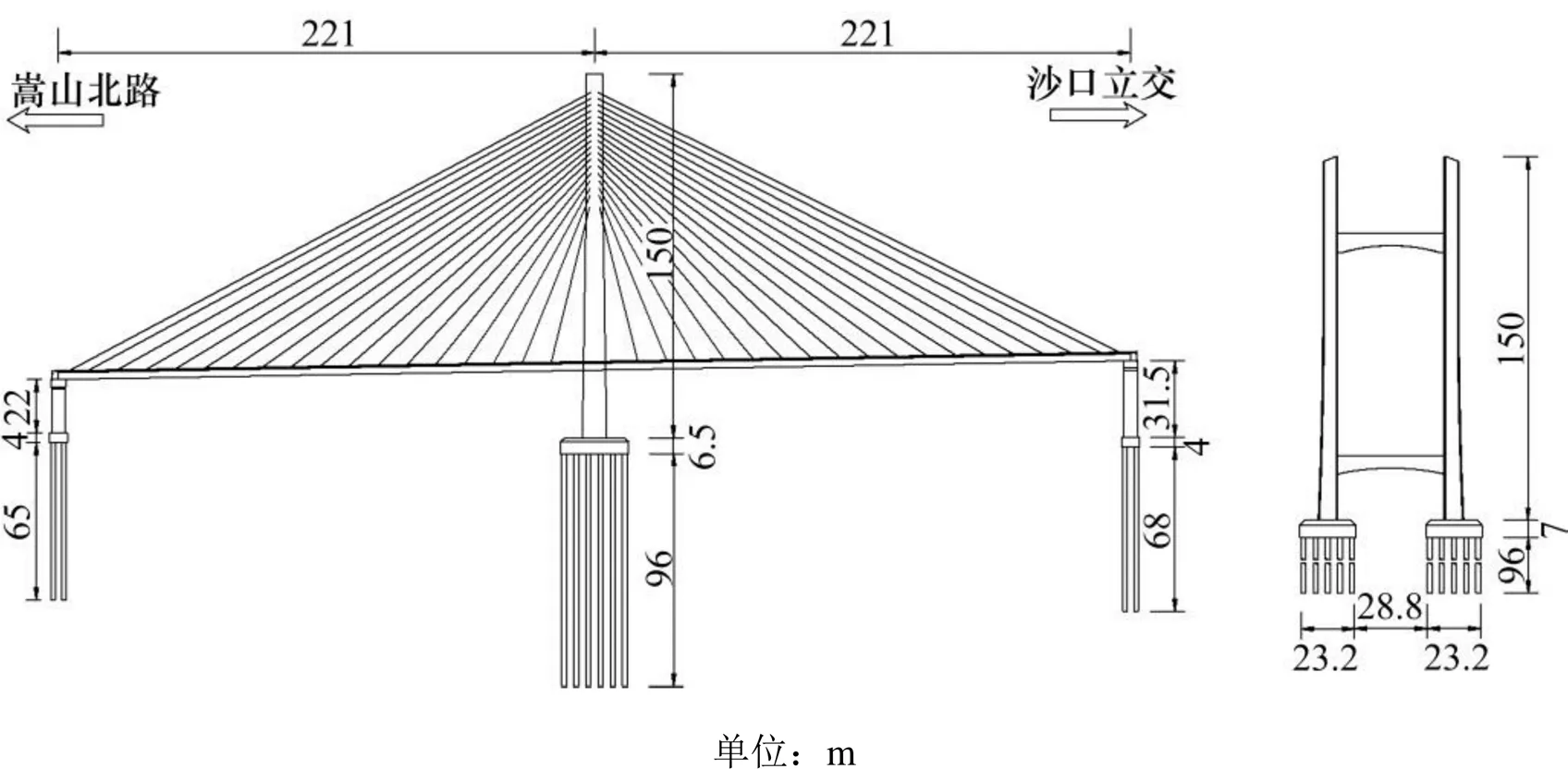
(a) 总体布置图；(b) 桥塔立面图

1.2 有限元分析模型

采用MIDAS/CIVIL 建立全桥动力模型，如图2所示，主塔、主梁、桥墩、承台、盖梁、桩基础均采用梁单元模拟，斜拉索采用桁架单元模拟,并采用Ernst等效弹模来考虑拉应力和自重垂度对拉索的影响[15]。全桥由3 362个节点和3 235个单元组成，其中包括3 163个梁单元和72个桁架单元。桩土作用采用弹簧模拟，弹簧刚度通过“m”法计算[16]。

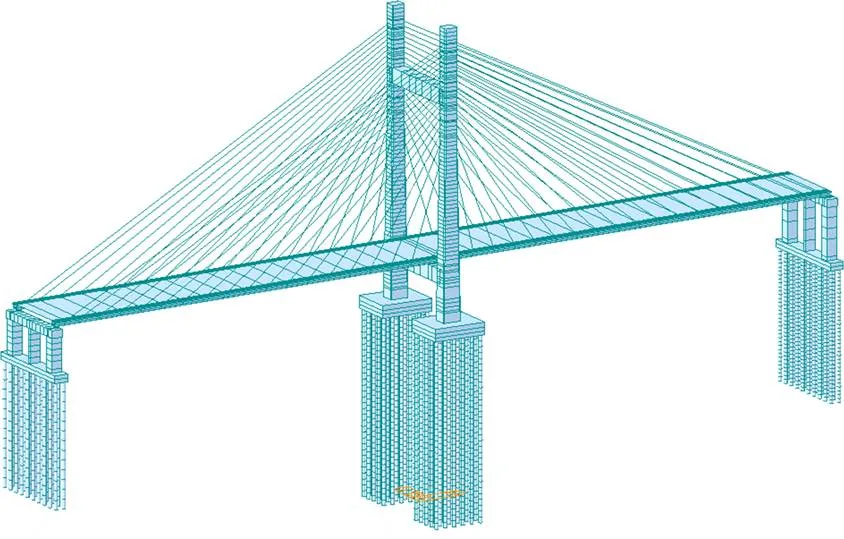
图2 有限元模型

Ernst公式如下：

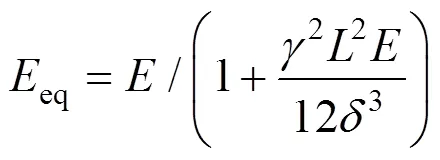
式中：eq为索的等效弹性模量；为索材料的弹性模量；为索的容重；为索的水平投影；为索的拉应力。

表1为斜拉桥的前五阶动力特性。

表1 斜拉桥动力特性

由表1可以看出，斜拉桥第1阶为主梁纵飘，第2阶和第5阶均为主梁竖向弯曲振动，第3阶为主塔横向弯曲振动，第4阶为主梁横向弯曲振动。

2 地震动输入

选用桥址安评报告中的3条地震波作为地震动输入(7度罕遇)，并通过调幅得到8度(=0.38)和9度(=0.64)罕遇地震各3条地震动。图3～图5为7度罕遇地震动加速度时程曲线。文中分别按顺桥向和横桥向两种方式输入地震动，输入时考虑竖向地震动，竖向加速度取为水平向的65%。

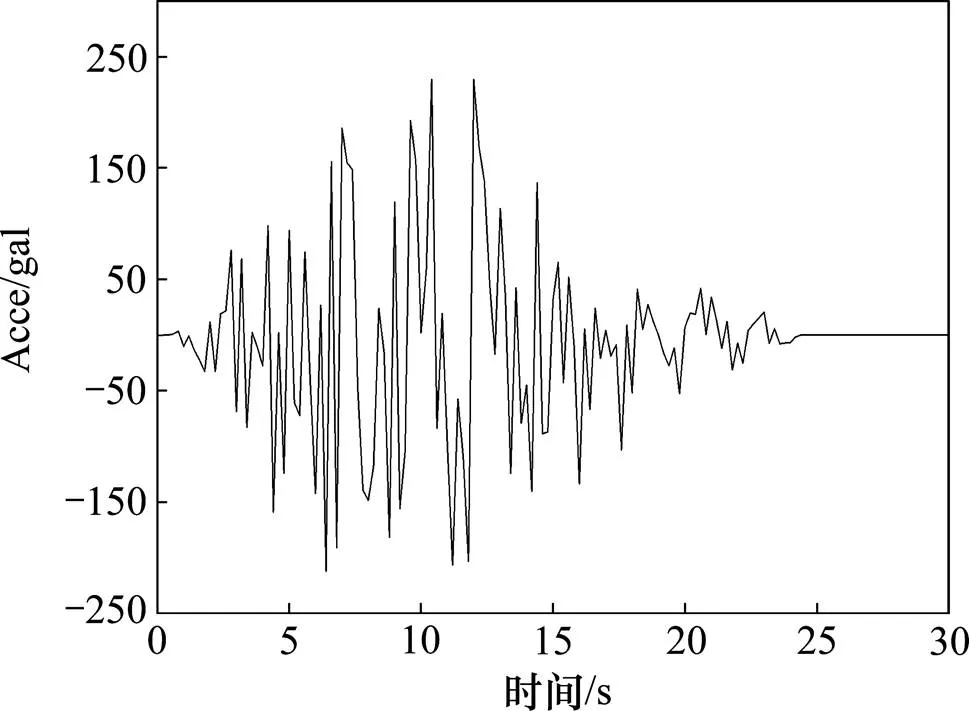
图3 地震动加速度时程曲线(wave1)

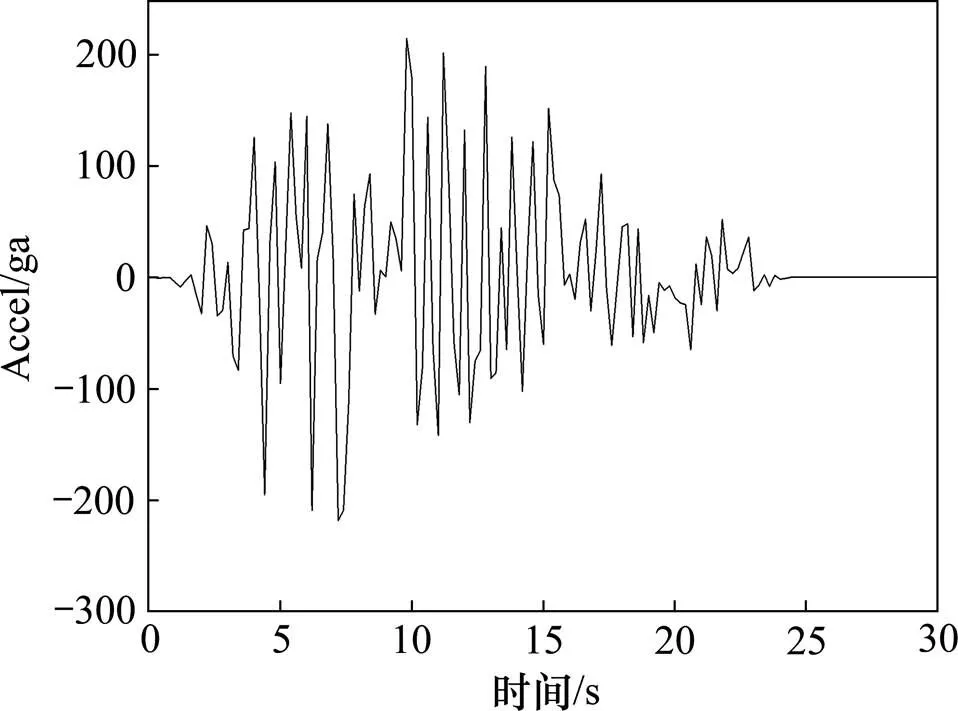
图4 地震动加速度时程曲线(wave2)

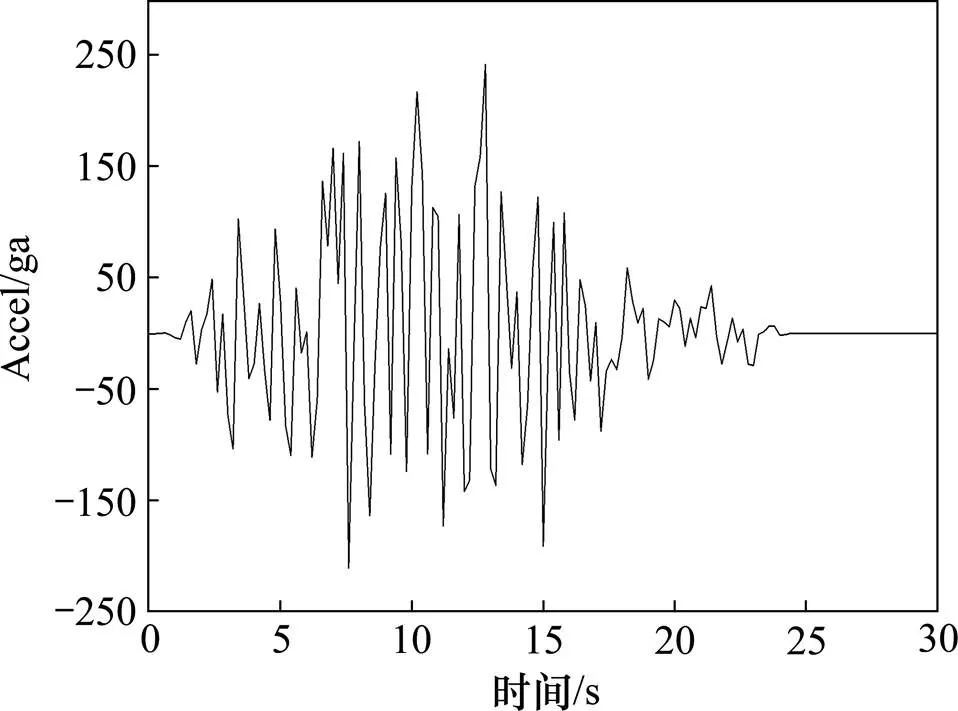
图5 地震波加速度时程曲线(wave3)

3 不同强度地震作用下拉索地震反应分析

本文采用非线性时程法进行拉索地震反应分析，计算时采用Rayleigh阻尼，阻尼比取0.03。文中分析了顺桥向和横桥向2种输入方式下拉索的地震反应。下文中出现的角度均代表拉索与水平面的立面夹角。

3.1 顺桥向输入时拉索地震反应

图6和图7分别为恒载下的索拉力和索应力，图8和图9分别为地震单独作用下的索拉力和索应力，拉索地震力为3条地震动作用下的最大索力。图10和图11为恒载和地震作用共同作用下的索拉力和索应力。表2为不同荷载工况下拉索内(应)力所占比重。

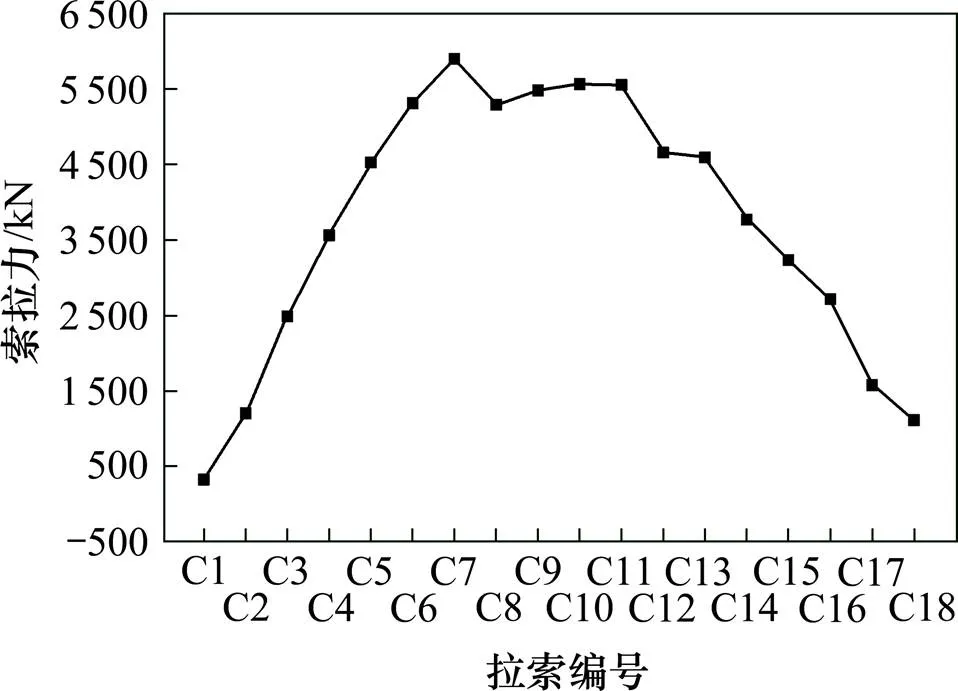
图6 恒载作用下拉索拉力

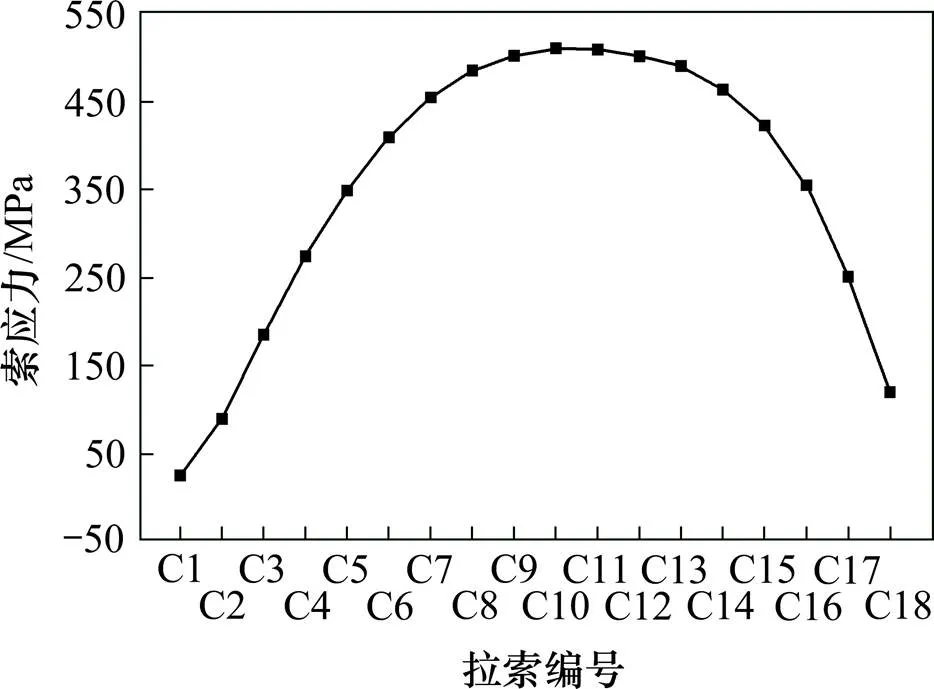
图7 恒载作用下拉索应力

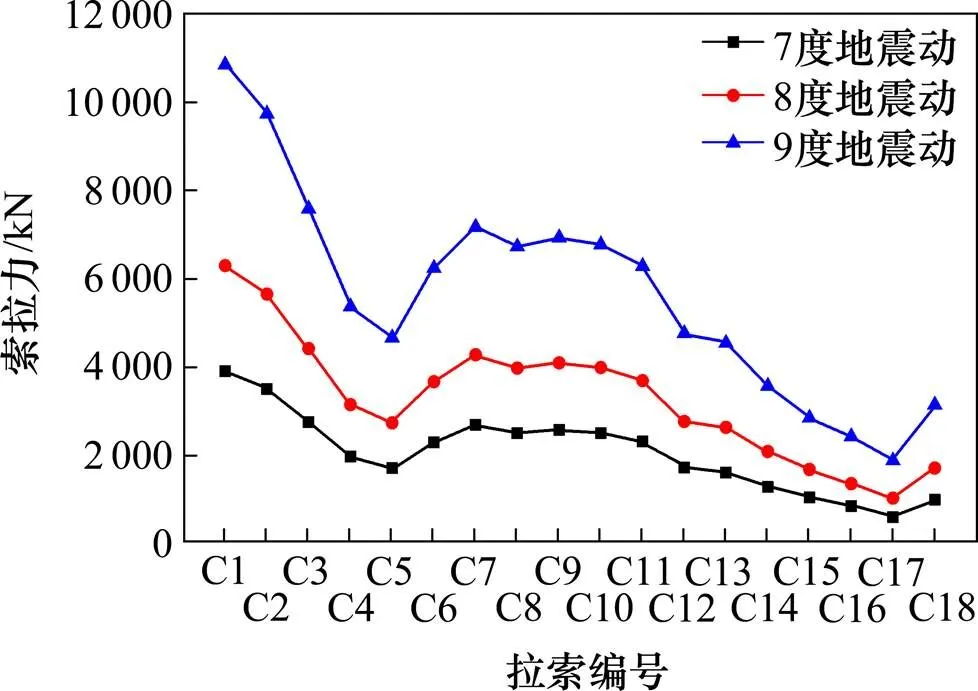
图8 不同强度地震动作用下拉索拉力

图9 不同强度地震动作用下拉索应力

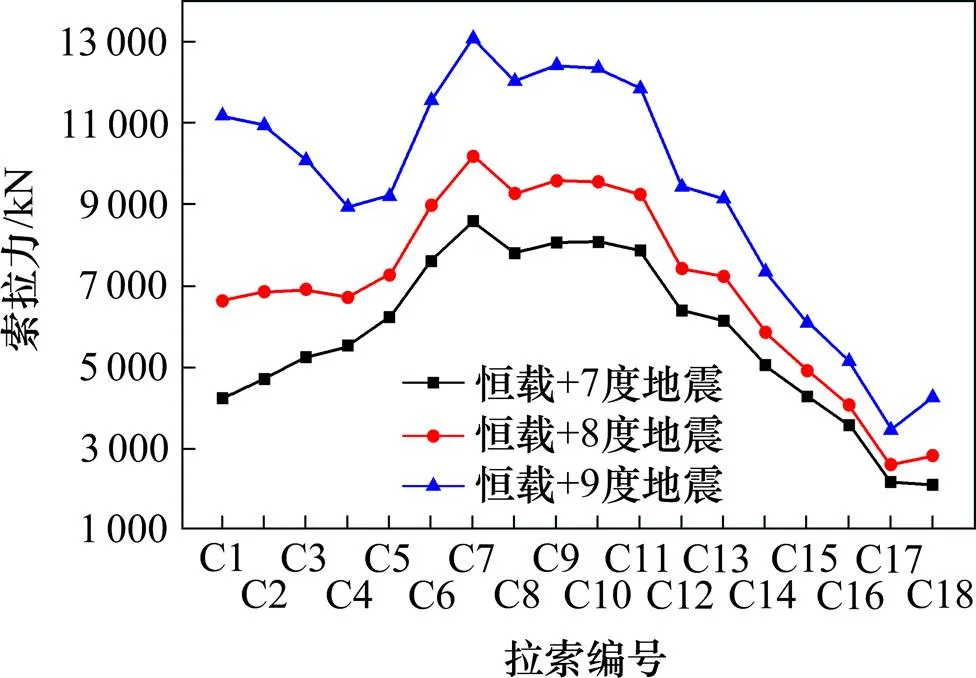
图10 恒载和不同强度地震动共同作用下拉索拉力

由图6可以看出，在恒载单独作用下，C7号拉索为最大拉力索，较大索力集中在跨中区域。拉索在26°～33°区域，索拉力随着角度的增大而增大；在34°～41°区域，索拉力基本不变；在41°～76°区域，索拉力随着角度的增大而减小。由图8和图10可以看出，随着地震动强度的增加，拉索的地震反应也相应的增大，在不同强度地震动单独作用下，C1号拉索(长索)为最大拉力索、与水平面夹角约为27°。在恒载和地震共同作用下，C7号拉索为最大拉力索、与水平面夹角约为33°，其角度与集集地震中集鹿大桥出现锚固失效的拉索角度(34°)相近，且都位于跨中区域。所以C7号拉索为地震中的最不利锚固索。

表2 不同荷载工况下索力所占比重

注：恒载比重=恒载下索力/恒载和地震共同作用下索力；地震比重=地震作用下索力/恒载和地震共同作用下索力。

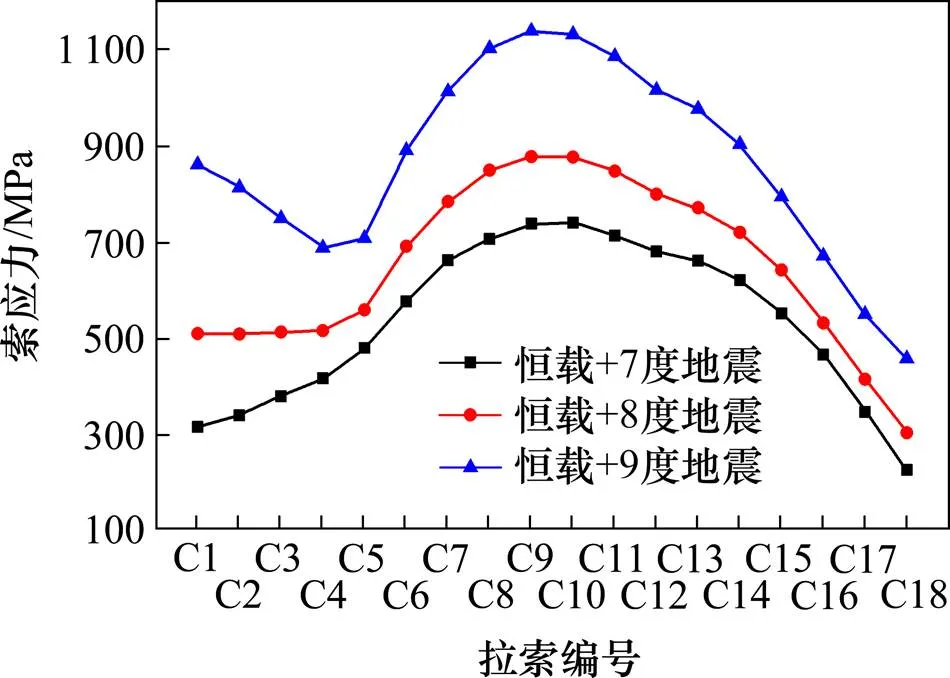
图11 恒载和不同度地震强度共同作用下拉索应力

由于拉索截面设计不同，最大拉力索并非最大拉应力索，由图11可以看出，在恒载和7度罕遇地震共同作用下，C10号拉索为最大拉应力索、与水平面夹角约为38°，最大索应力为741 MPa；在恒载分别与8度和9度罕遇地震共同作用下，C9号拉索为最大拉应力索、与水平面夹角约为36°，最大索应力分别为878 MPa和1 139 MPa。较大拉应力索集中在跨中(约35°～44°)区域。

3.2 横桥向输入时拉索地震反应

图12和图13分别为不同强度地震动单独作用下拉索的索拉力和索应力，图14和图15分别为恒载和不同强度地震动共同作用下拉索的索拉力和索应力，表3为不同荷载工况下拉索力所占比重。

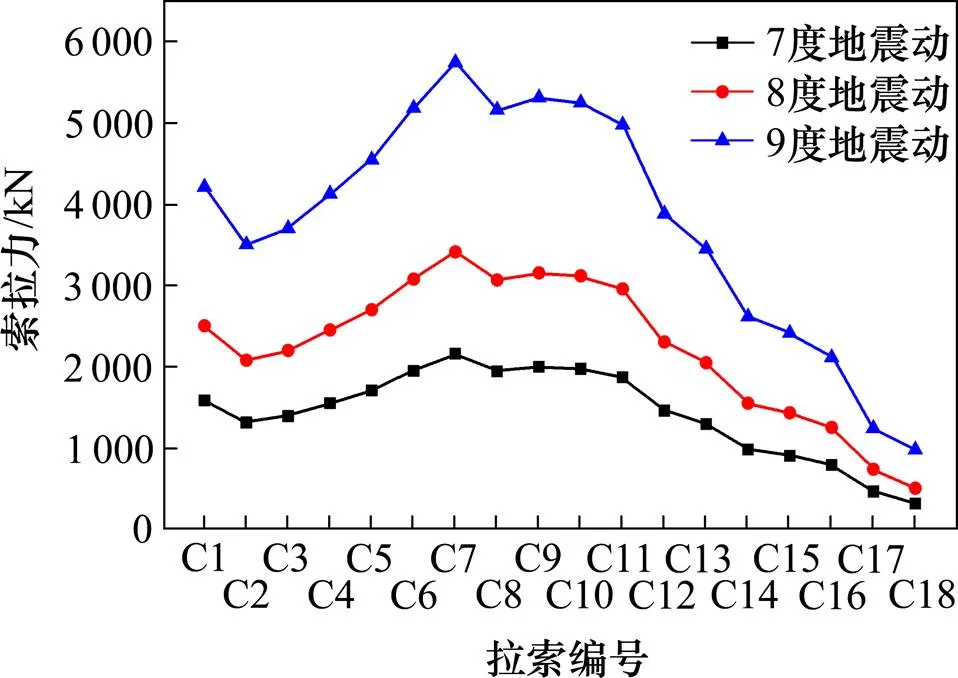
图12 不同强度地震动作用下拉索拉力

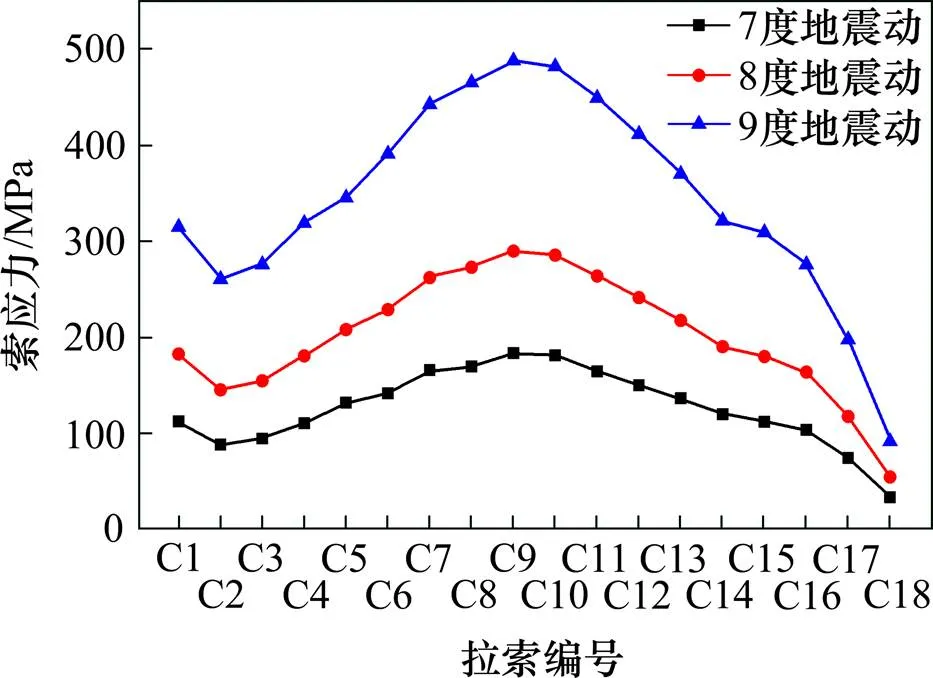
图13 不同强度地震动作用下拉索应力

由图12和图14可以看出，随着地震动强度的增加，拉索的地震反应也相应的增大，在不同强度地震动单独作用下，C1号拉索为最大拉力索、与水平面夹角约为27°。在恒载和地震共同作用下，C7号拉索为最大拉力索、与水平面夹角约为33°，所以C7号拉索为地震中的最不利锚固索。

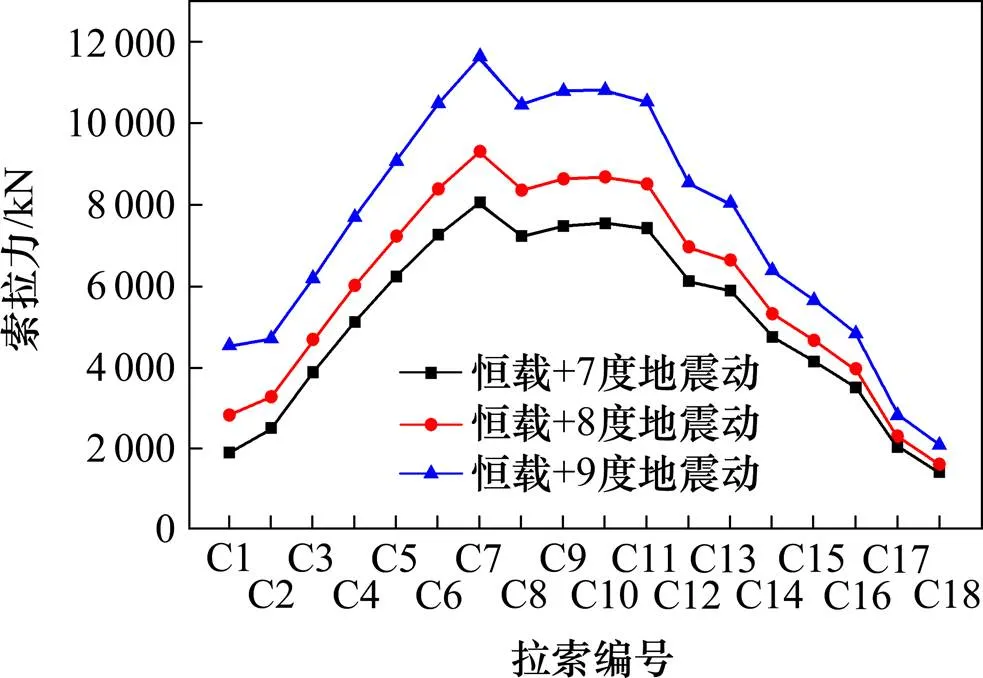
图14 恒载和不同强度地震动共同作用下拉索拉力

由图15可以看出，在恒载和不同强度地震共同作用下，C10号拉索为最大拉应力索、与水平面夹角约为38°，最大索应力分别为692，796及992 MPa。较大拉应力索同样集中在跨中(约35°～44°)区域。由表2和表3可以看出，在不同输入方式下，随着地震强度的增加，拉索地震反应也随之增大，地震比重也变大。顺桥向输入时的拉索地震反应大于横桥向输入，设计时顺桥向输入的拉索地震反应起控制作用。

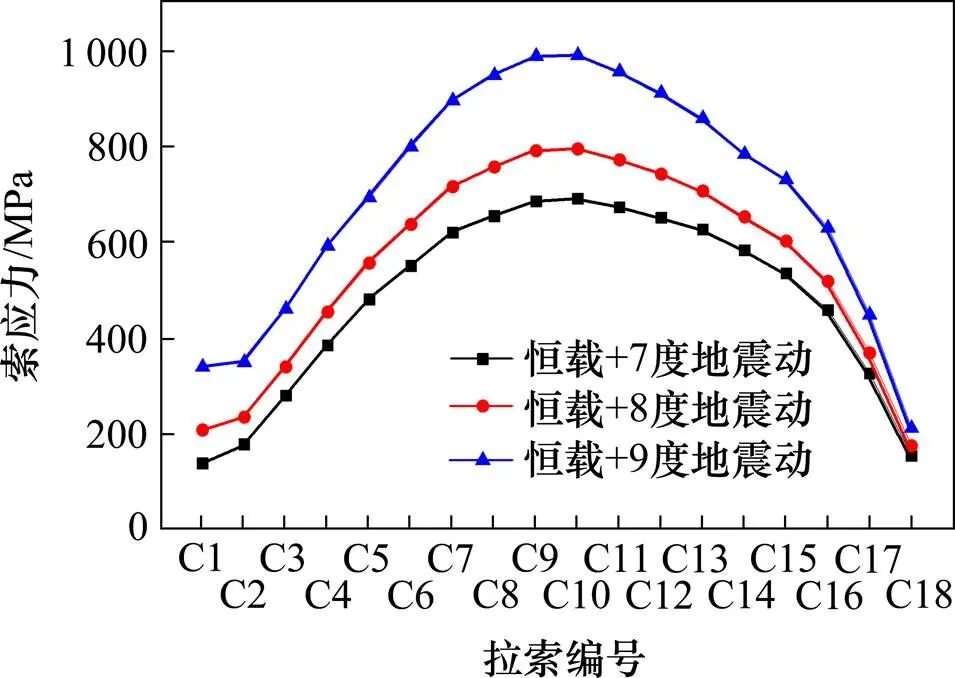
图15 恒载和不同强度地震动共同作用下拉索应力

表3 不同荷载工况下索力所占比重

4 结论

1) 与水平面夹角约33°的拉索为最大拉力索，该索为最不利锚固索，其与集集地震中集鹿大桥出现锚固失效的拉索角度(34°)相近，且都位于跨中区域，应引起设计的注意。

2) 顺桥向输入时，最不利拉应力索的位置随地震强度的增加而改变，但其与水平面夹角介于36°～38°之间。

3) 横桥向输入时，最不利拉应力索的位置不随地震强度的增加而改变，其与水平面夹角约呈38°。

4) 顺桥向输入时拉索地震反应大于横桥向输入，设计时应按顺桥向输入时的索力进行设计。

[1] 冯莉, 樊燕燕, 王力, 等. 基于性能的高速铁路钢管混凝土拱桥地震经济风险分析[J]. 铁道科学与工程学报, 2019, 16(3): 573−580. FENG Li, FAN Yanyan, WANG Li, et al. Performance-based seismic financial risk assessment of a CFST arch bridge over high-speed railway[J]. Journal of Railway Science and Engineering, 2019, 16(3): 573−580.

[2] 王海飙, 徐文静. 基于AHP-熵物元的地震安全社区应急管理评价[J]. 中国安全生产科学技术, 2019, 15(6): 55−60.WANG Haibiao, XU Wenjing. Evaluation on emergency management of earthquake safety community based on AHP-entropy matter-element[J]. Journal of Safety Science and Technology, 2019, 15(6): 55−60.

[3] 夏修身, 李建中, 管仲国, 等. 斜拉桥桥塔非线性抗震性能研究[J]. 中国公路学报, 2016, 29(3): 66−72, 81.XIA Xiushen, LI Jianzhong, GUAN Zhongguo, et al. Nonlinear seismic performance investigation of cable- stayed bridge towers[J]. China Journal of Highway and Transport, 2016, 29(3): 66−72, 81.

[4] 吴庆雄, 王文平, 陈宝春. 多索-梁结构固有振动特性分析[J]. 工程力学, 2017, 34(1): 109−116. WU Qingxiong, WANG Wenping, CHEN Baochun. Natural vibration analysis of multi-cables-stayed beam structure[J]. Engineering Mechanics, 2017, 34(1): 109− 116.

[5] CHANG K C, MO Y L, CHEN C C, et al. Lessons learned from the damaged Chi-Lu cable-stayed bridge[J]. Journal of Bridge Engineering, 2004, 9(4): 343−352.

[6] 宋涛, 宋一凡, 贺拴海, 等. 基于索梁权矩阵的矮塔斜拉桥索力优化[J]. 武汉大学学报(工学版), 2016, 49(2): 259−263. SONG Tao, SONG Yifan, HE Shuanhai, et al. Optimization for cable force of extradosed cable-stayed bridge based on cable/girder weight matrix[J]. Journal of Wuhan University (Engineering Science), 2016, 49(2): 259−263.

[7] 陈志军, 刘洋, 杨立飞, 等. 基于粒子群优化算法的独塔斜拉桥成桥索力优化[J]. 桥梁建设, 2016, 46(3): 40− 44. CHEN Zhijun, LIU Yang, YANG Lifei, et al. Optimization of stayed tention of completed bridge of single-pylon cable-stayed bridge baseded on particle swarm optimization algorithm[J]. Bridge Construction, 2016, 46(3): 40−44.

[8] 何旭辉, 杨贤康, 朱伟. 钢桁梁斜拉桥成桥索力优化的实用算法[J]. 铁道学报, 2014, 36(6): 99−106. HE Xuhui, YANG Xiankang, ZHU Wei. Practical algorithm for optimization of cable forces in completion of steel truss girder cable-stayed bridges[J]. Journal of the China Railway Society, 2014, 36(6): 99−106.

[9] REN W X, Obata M. Elastic-plastic seismic behavior of long span cable-stayed bridges[J]. Journal of Bridge Engineering, 1999, 4(3): 194−203.

[10] Nazmy A S, Abdel-Ghaffar A M. Non-linear earthquake- Response analysis of long-span cable-stayed bridges: Theory[J]. Earthquake Engineering & Structural Dynamics, 1990, 19(1): 45−62.

[11] Nazmy A S, Abdel-Ghaffar A M. Non-linear earthquake- response analysis of long-span cable-stayed bridges: Applications[J]. Earthquake Engineering & Structural Dynamics, 1990, 19(1): 63−76.

[12] XIA Y, Fujino Y. Auto-parametric vibration of a cable- stayed-beam structure under random excitation[J]. Journal of Engineering Mechanics, 2006, 132(3): 279− 286.

[13] 叶爱君, 苏振宇. 超大跨径斜拉桥斜拉索局部振动对地震反应的影响[J]. 同济大学学报(自然科学版), 2010, 38(2): 158−163. YE Aijun, SU Zhenyu. Effect of cable vibrition on seismic response of supper-long span cable-stayed bridge [J]. Journal of Tongji University (Natural Science), 2010, 38(2): 158−163.

[14] 易江, 莫金生, 李建中. 强震作用下独塔斜拉桥拉索松弛现象研究[J]. 工程力学, 2018, 35(6): 97−104. YI Jiang, MO Jinsheng, LI Jianzhong. Study on cable relaxation of signle-tower cable-stayed bridge due to strong earthquake[J]. Engineering Mechanics, 2018, 35(6): 97−104.

[15] 初明进, 周育泷, 陆新征, 等. 钢筋混凝土单向梁板子结构抗连续倒塌试验研究[J]. 土木工程学报, 2016, 49(2): 31−40. CHU Mingjin, ZHOU Yulong, LU Xinzheng, et al. An experimental study on one-way reinforced concrete beam-slab substructures for resisting progressive collapse [J]. China Civil Engineering Journal, 2016, 49(2): 31− 40.

[16] 叶爱君. 桥梁抗震[M]. 北京: 人民交通出版社, 2017. YE Aijun. Seismic design of bridge[M]. Beijing: China Communication Press, 2017.

Study on cable seismic performance of a long-span cable-stayed bridge with single tower

LEI Liben1, XIA Xiushen1, DAI Xiaochun2, WANG Jinbo1, HAN Sen1

(1. School of Civil Engineering, Lanzhou Jiaotong University, Lanzhou 730070, China;2. China Railway Eryuan Engineering Group Co., Ltd., Chengdu 610031, China)

In order to study the cable seismic response, a full-span single-stayed cable-stayed bridge was used as the engineering background. The full bridge finite element model was established using MIDAS CIVIL software. Earthquakes with different intensities at the E2 level were input to the longitudinal and transverse bridges, and the seismic response of the stay cables was analyzed by a non-linear time-history analysis method. Examined the variation of the position of the most unfavorable cable with earthquake intensity. The results show that the C7 cable with an angle of about 33° to the horizontal plane is the maximum tension cable, which is the most unfavorable anchor cable. The cable in the region with an angle of about 36° to 38° to the horizontal plane is the maximum tensile cable, which is the most Unfavorable stress. The seismic response of the cable when bridge is input thelongitudinal earthquakes is more unfavorable than when bridge is input the transverse earthquakes. The research results can be used for reference during design.

cable-stayed bridge; cable; earthquake response; cable-girder anchorage

TU443.22；U442.55

A

1672 − 7029(2020)11 − 2857 − 07

10.19713/j.cnki.43−1423/u.T20200044

2020−01−12

国家自然科学基金资助项目(51668035)

夏修身(1978−)，男，安徽涡阳人，教授，博士，从事桥梁抗震研究；E−mail：xiaxiushen@mail.lzjtu.cn

(编辑 蒋学东)