考虑拉力场的钢板梁抗剪承载力计算

李立峰，郭艳艳，程子涵，孙敬凯

考虑拉力场的钢板梁抗剪承载力计算

李立峰1, 2，郭艳艳1，程子涵1，孙敬凯3

(1. 湖南大学 土木工程学院，湖南 长沙 410082；2. 风工程与桥梁工程湖南省重点实验室，湖南 长沙 410082；3. 云南武倘寻高速公路有限责任公司，云南 昆明 650000)

针对采用拉力场计算的腹板发生弹性剪切屈曲的钢板梁抗剪承载力的可靠性进行分析，并针对不产生腹板弹性剪切屈曲的钢板梁提出抗剪承载力计算方法，设计完成4个钢板梁抗剪模型试验，掌握其破坏模式和特征，获得顶底板弯曲应变及面内变形、腹板主拉应变及面外变形；根据试验现象，提出适用于不产生腹板弹性剪切屈曲的钢板梁抗剪的扩展拉力场理论，提出相应的计算公式；并采用ABAQUS软件建立试验梁空间有限元模型，理论仿真与试验结果吻合良好。研究结果表明：对于腹板产生弹性剪切屈曲的钢板梁，采用Rockey理论计算的抗剪承载力精度较高，对于腹板不产生弹性剪切屈曲的钢板梁，抗剪破坏时也发展了拉力场机制，采用本文提出的扩展拉力场理论计算公式具有较高精度，可为实际工程与规范提供参考价值。

钢板梁；拉力场理论；旋转应力场理论；屈曲后强度；抗剪承载力

近年来，我国钢板梁的建设得到大力发展、应用前景非常广阔。钢板梁的抗剪破坏机理及计算方法一直是研究热点，现有的钢板梁抗剪承载计算理论可归纳为2类，一类是不考虑屈曲后强度；另一类是考虑屈曲后强度，代表理论为拉力场和旋转应力场理论[1]。现有拉力场理论主要包括Basler[2]理论和Rockey[3]理论，区别在于Basler理论忽略翼缘刚度对钢板梁抗剪承载力的影响，假定拉力带产生于加劲肋之间，而Rockey理论则考虑翼缘刚度的影响，假定拉力带产生于翼缘塑性铰之间。之后，众多学者通过大量试验、仿真与理论研究，以拉力场理论为基础对钢板梁抗剪计算理论进行了修正与完善。段兰等[4]通过4片高强度工字梁腹板试验，分析了腹板高厚比、翼缘约束效应等对抗剪承载力的影响；童根树等[5]提出了翼缘对腹板转动约束的合理参数，给出了考虑综合翼缘影响的抗剪公式；康孝先等[6]提出考虑翼缘抗弯刚度与腹板弯曲刚度的翼缘嵌固系数，提出了修正拉力场理论。Davies等[7-9]学者也进行了钢板梁抗剪研究。度计算钢板梁抗剪承载力的拉力场理论已经很成熟，但因理论假定腹板发生剪切弹性屈曲，导致无法应用到腹板不发生剪切屈曲的钢板梁抗剪计算中。旋转应力场理论虽然可以计算腹板不发生剪切屈曲的钢板梁抗剪承载力，抗剪承载力由腹板作用及翼缘作用两项组成，但翼缘抗剪公式中塑性铰间宽度是根据试验总结的经验公式，大多数规范假定剪力完全由钢梁腹板承担，计算结果比较保守。因此本文通过不同腹板厚度的钢板梁抗剪试验，分析钢板梁的受力性能、破坏模式，获得抗剪承载力，对比腹板是否发生弹性剪切屈曲的2种钢板梁的受力特性与破坏模式的区别，对Rockey理论的计算公式进行修正，使其适用于腹板不发生剪切屈曲的钢板梁抗剪承载力计算。并建立有限元模型，与理论及试验结果、各国规范结果进行对比，验证结果准确性，对规范提出建议。

1 钢板梁抗剪承载力计算理论

本节先介绍具有代表性的钢板梁抗剪理论，并基于Rockey拉力场理论提出适用于不产生腹板弹性剪切屈曲的钢板梁抗剪承载力计算的扩展拉力场理论。

1.1 考虑屈曲后强度的钢板梁抗剪理论

1.1.1 拉力场理论

拉力场理论作为重要的考虑屈曲后强度的钢板梁抗剪理论，有2个基本假定：一是极限状态下的应力满足Mises屈服准则，二是腹板达到剪切屈曲后，任何屈曲后的贡献由拉力场承担。现有的拉力场理论主要包括Basler理论和Rockey理论。

1) Basler理论

Basler理论不考虑翼缘刚度的影响，假定拉力带形成于加劲肋之间，如图1。抗剪承载力由梁作用与拉力场作用组成[3]。AISC1997，AASHTO 2012采用了此模型。

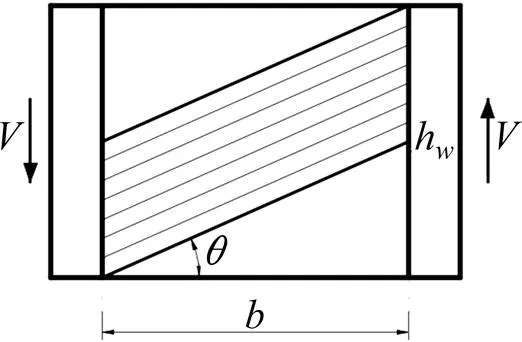
图1 Basler拉力场模型

2) Rockey理论

Rockey理论考虑了翼缘刚度的影响，假定拉力带产生于翼缘塑性铰之间。抗剪承载力由翼缘作用、拉力场作用与梁作用组成[6]，且全式只有一个变量。Eurcode 3拉力场方法采用了此模型。

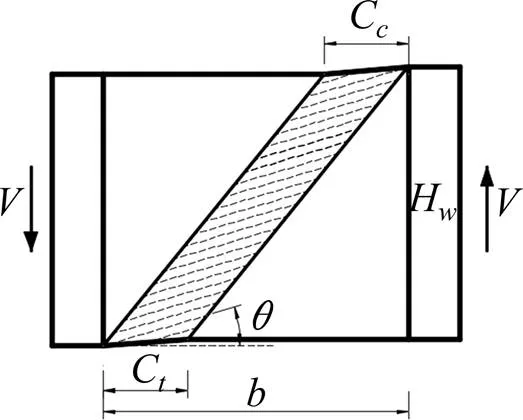
图2 Rockey拉力场模型

1.1.2 旋转应力场理论

旋转应力场理论有2个基本假定：一是当腹板屈曲后，主压应力不变且等于剪切屈曲应力，主拉应力由膜应力角度确定；二是只在翼缘处形成拉力带，且翼缘之间拉力场的形成不改变腹板之前的抗剪承载力。

利用旋转应力场理论计算钢板梁的抗剪承载力由梁作用与翼缘作用组成[1]，如图3，EC3与GB50017采用了旋转应力场理论。

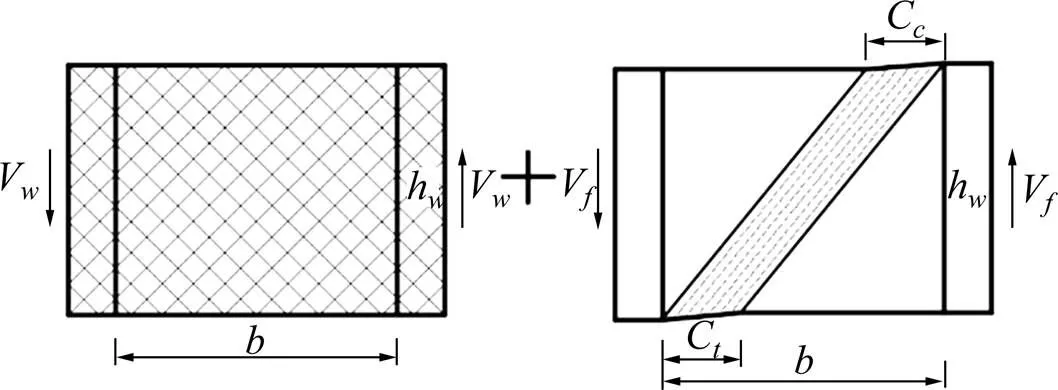
图3 旋转应力场模型

1.2 本文提出的扩展拉力场理论

虽然利用屈曲后强度计算钢板梁抗剪承载力的拉力场理论已经很成熟，但对于腹板不会发生剪切屈曲的钢板梁，无法考虑屈曲后强度，Rockey拉力场理论不再适用。通过本文钢板梁抗剪实验现象发现，无论钢板梁腹板是否产生弹性剪切屈曲，发生抗剪破坏时均发展了拉力场机制，区别仅在于发展拉力场的时机与程度大小。因此本文通过钢板梁试验结果分析了是否发生腹板剪切屈曲的钢板梁的不同的受力特征，以下面的基本假定为基础，对Rockey拉力场理论中3种作用的计算公式分别进行修正，使其适用于腹板不发生弹性剪切屈曲的钢板梁抗剪承载力计算。

1.2.1 基本假定

1) 腹板屈服后，主压应力不变，任何屈服后的贡献由拉力场承担；

2) 只在翼缘处形成拉力带，且不考虑钢材的强化效应，即翼缘之间拉力场的形成不改变腹板之前的抗剪承载力。

1.2.2 计算公式

基于上述假定对Rockey理论求解钢板梁抗剪的公式进行修正，包括以下3项：

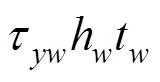
2) 拉力场对腹板抗剪的贡献：Rockey理论认为当腹板产生剪切屈曲后开始发展拉力场；对于腹板不发生剪切屈曲的钢板梁，腹板直到全截面屈服失效后，主压应力不变，拉力带才在主拉应力下形成，见图4，但此项相比考虑屈曲后强度时拉力场对钢板梁腹板的抗剪贡献小得多，因此本文假定忽略钢材的强化作用，此项作用作为安全储备；

3) 拉力场对翼缘抗剪的贡献：拉力带作用下上下翼缘产生的塑性铰对抗剪也有一定的贡献。塑性铰产生于弯矩最大而剪力为0的位置，将图4中上翼缘ABC取出单独进行受力分析：

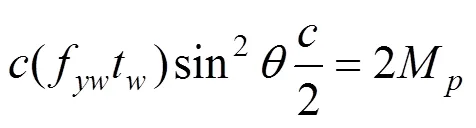
(2)

采用本文提出扩展拉力场理论，计算不发生腹板弹性剪切屈曲的钢板梁抗剪承载力的公式如下，全式只有一个变量，公式中C与C按式(2)求解：

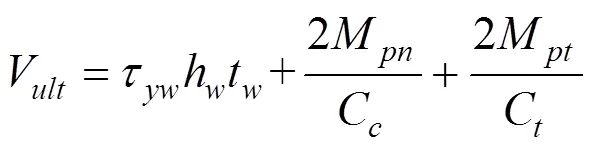
下文拟通过模型试验结果与仿真结果来证明本文扩展拉力场理论的可靠性。

2 模型试验

2.1 试件设计

为研究腹板发生剪切屈曲与不发生剪切屈曲的钢板梁关于拉力场抗剪的不同破坏特性，本文设计了2片钢板梁共4次抗剪承载力试验，见图6，在第一次加载前，对短边腹板两侧受压对角线各焊接两条受压板件并用混凝土块进行填充加固，避免进入塑性，一侧破坏后，对破坏侧进行加固，并取消加强侧的钢板，再次进行另一侧加载。4片加载试件的尺寸除了腹板厚度、宽度不同，其余尺寸均相同，其中顶板尺寸为250 mm×25 mm，底板尺寸为250 mm×16 mm，具体尺寸见表1及图5。

表1 试验梁腹板尺寸

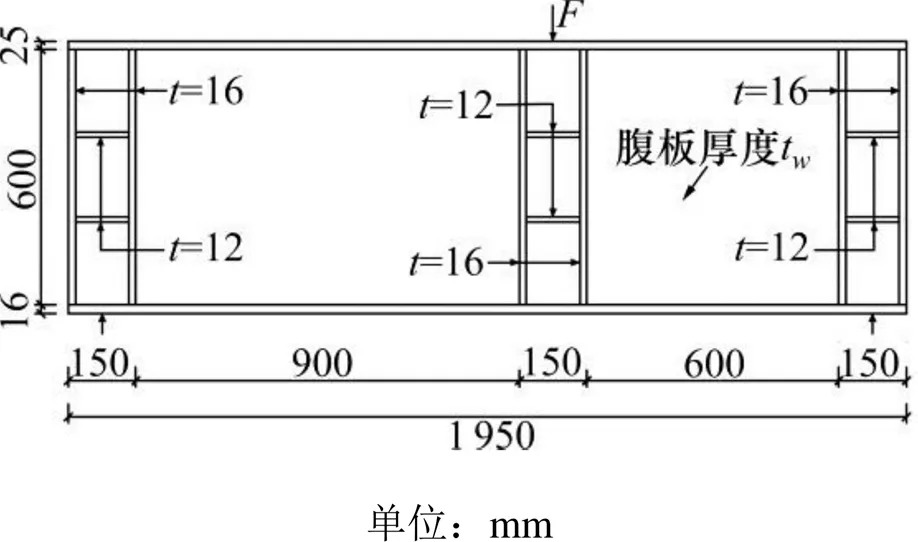
图5 试验梁尺寸

试验用钢材为Q345b，弹性模量为206 000 MPa，实测屈服强度为383.1 MPa。钢梁的本构关系采用双线性随动强化模型。

2.2 加载及测试方案

2.2.1 加载方案

试验梁采用2 500 kN液压千斤顶在中间加劲肋位置处进行简支加载，如图6所示。

图6 试验梁加载方案

2.2.2 测试方案

试验中，钢梁腹板对角线布置应变花、顶底板布置应变片，数量较多、以跟踪腹板屈服位置，具体布置如图7所示。简支和加载处均布置了百分表测量竖向位移，同时采用非接触式方法测量试件的变形以及腹板的应变场。

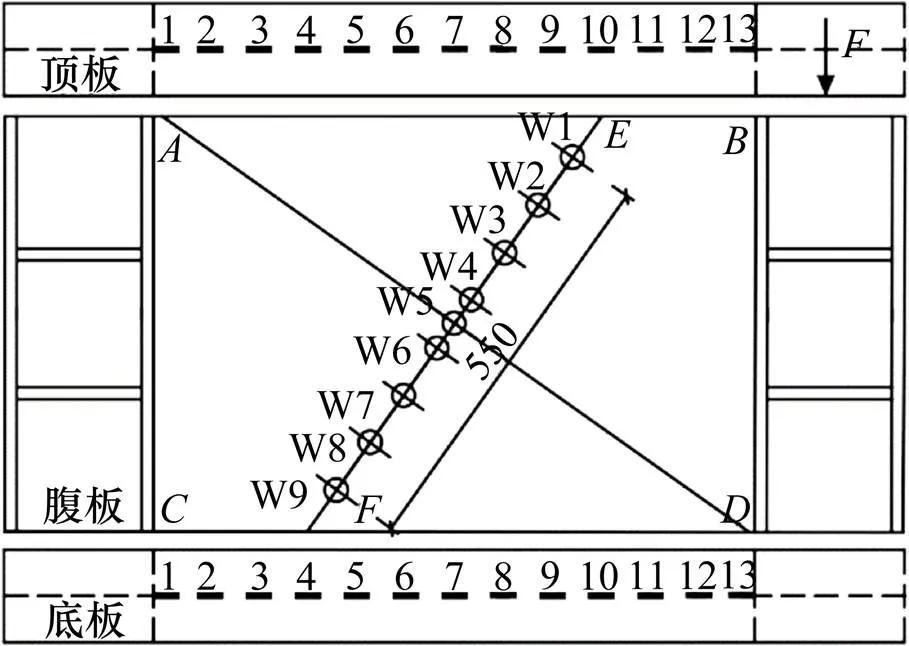
图7 试验梁测试方案

2.3 试验结果

2.3.1 破坏现象

试验梁SPG1-1与SPG1-2、试验梁SPG2-1与SPG2-2的破坏现象和受力特征基本一致。

对于腹板发生剪切屈曲的试验梁，以SPG1-2为例，当荷载较小时，加载端位移增长缓慢，结构处于弹性阶段；荷载继续增加到280 kN时，腹板开始出现面外变形、中心区域出现屈服失效；继续加载，腹板面外变形逐渐明显，腹板失效区域逐渐增大；加载到400 kN时，腹板大部分区域失效，结构接近破坏时、不能继续承载，由顶、底板和加劲肋组成的“空腹梁”继续承力，当框架形成塑性铰并扩展形成机动机构后，极限承载能力达到411 kN。卸载后测得腹板的面外残余变形，最大达到了26 mm，位于腹板中心位置。

图8 SPG1-2破坏现象

对于腹板不会发生剪切屈曲的试验梁，以SPG2-2为例，加载前期受力特征与薄腹板试验梁基本相同，但加载前期，腹板主应变沿对角线基本呈对称分布；加载到1 080 kN时，腹板开始屈服；继续加载，屈服区域逐渐扩大，顶底板塑性铰开始产生；直到腹板全截面失效不能承载后，腹板才产生面外变形；当全部塑性铰产生并扩展形成机动机构时，极限承载能力达到1 400 kN。卸载后测得腹板的面外残余变形，最大达到了36 mm，位于腹板中心位置。

图9 SPG2-2破坏现象

2.3.2 荷载-位移曲线

图10给出了4次试验梁加载点处的荷载-位移曲线。结果显示：加载前期，梁的刚度很大，位移增加缓慢，结构处于弹性阶段；继续加载，腹板逐渐失效并在翼缘产生塑性铰后，梁的刚度急剧下降，各试验梁的最终变形均超过200 mm。

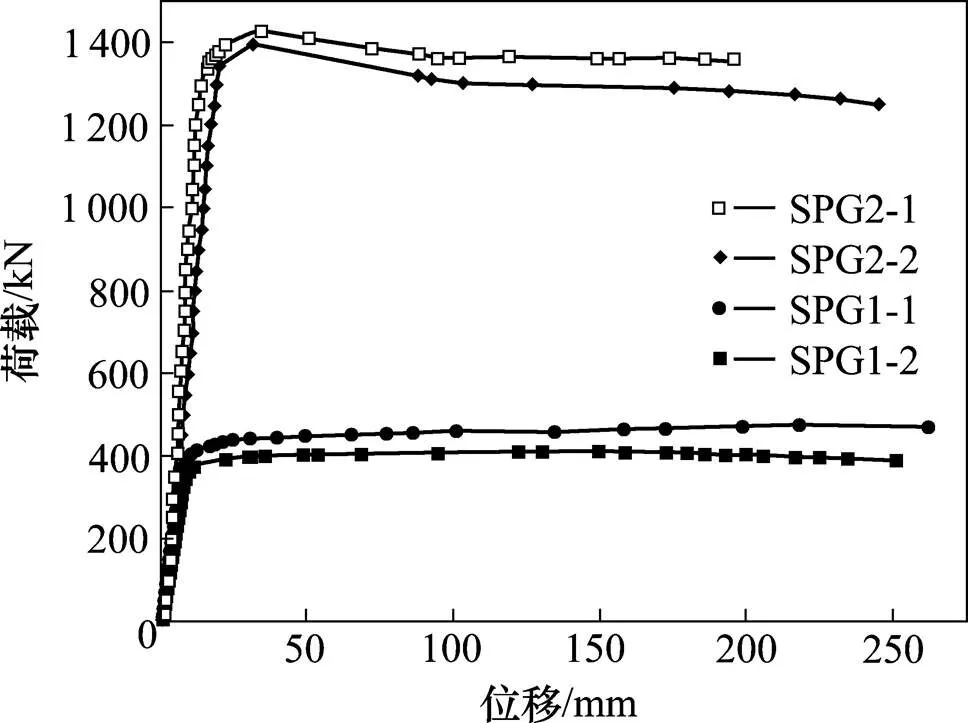
图10 荷载-位移曲线

2.3.3 应变分布规律

1) SPG1-2应变分布

①腹板应变

图11展示了简支梁腹板各应变花测得的主拉应变，原点位于腹板中心，横坐标为应变花测点在垂直于主对角线的位置，参照图9。腹板应变沿对角线应基本对称，随着荷载的增大，腹板屈服失效区域由对角线中心逐渐向两侧扩展。

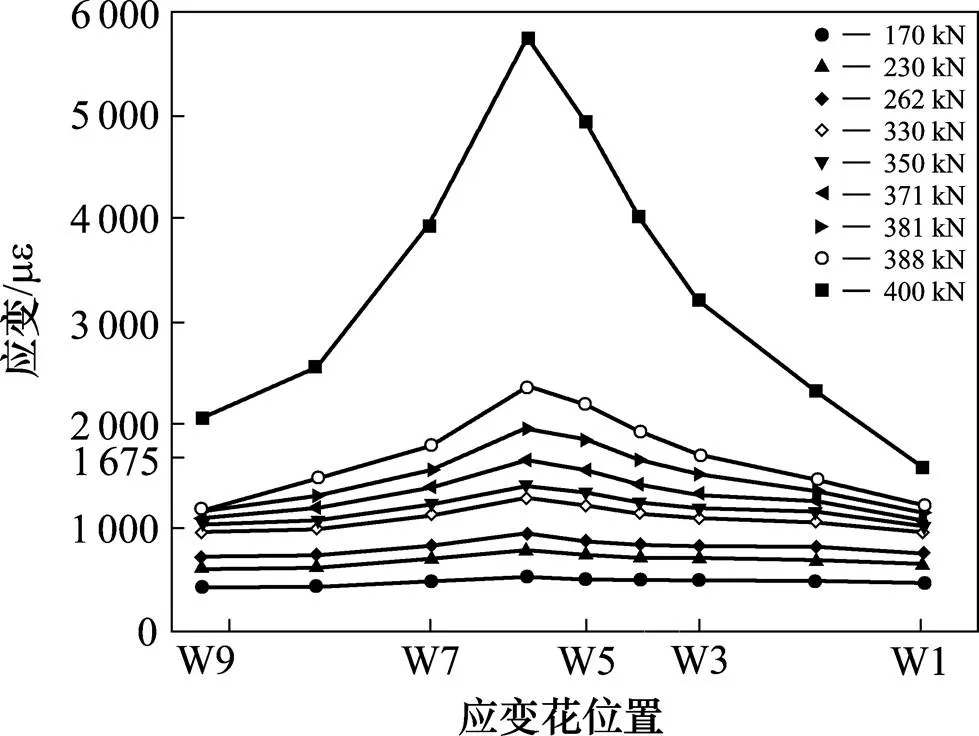
图11 腹板主拉应变-位置曲线

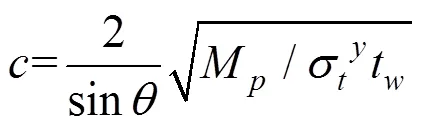
②顶、底板应变

图12～13展示了简支梁顶板、底板的弯曲应变。由图可以看出，达到极限荷载时，顶板之间的塑性铰形成于距离简支端0.57处，最终扩展范围达到0.57～0.69；底板之间的塑性铰形成于距离简支端0.61处，最终扩展范围达到甚至超过 0.52～0.7，与理论计算以及腹板应变推测的塑性铰位置相差不大，进一步验证了考虑屈曲后强度的拉力场理论的准确性。

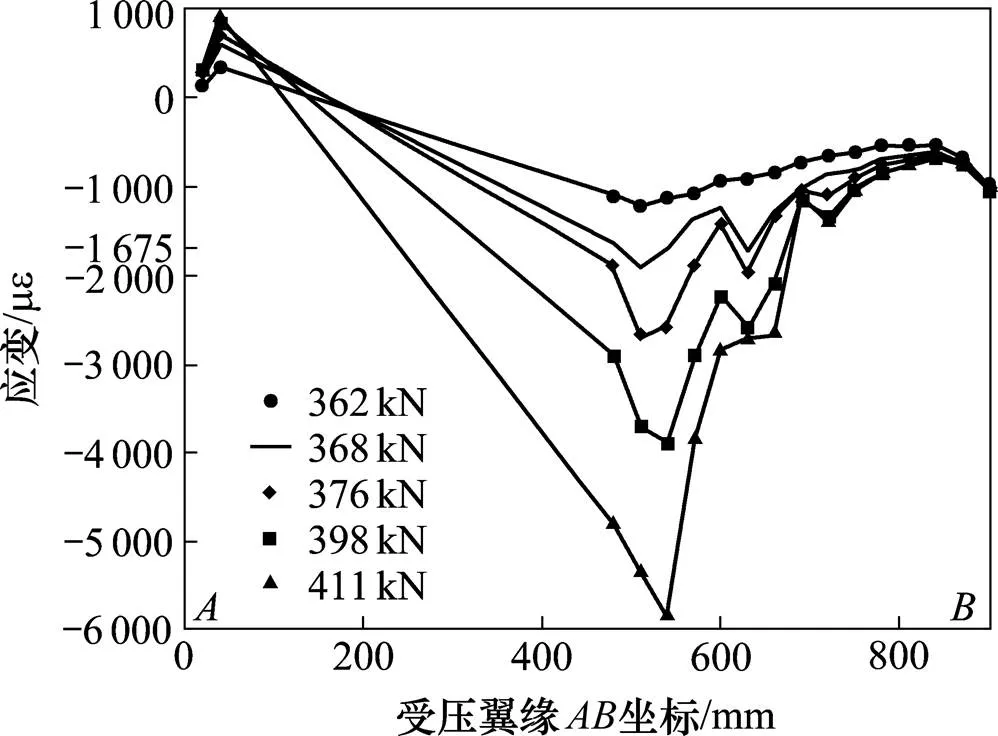
图12 受压翼缘应变-位置曲线

2) SPG2-2应变分布

①腹板应变

图14展示了简支梁腹板应变花测得的主拉应变，原点位于腹板中心，横坐标为应变花测点在垂直于主对角线的位置，参照图9。加载前期，腹板主应变沿对角线基本呈对称均匀分布，加载到1 080 kN时，腹板开始屈服；继续加载，屈服区域逐渐扩大，但在主对角线上呈无规不均匀状态，腹板未全截面失效。

由图可以推断出，达到极限荷载时，腹板的失效区域达到44%，根据腹板的失效位置，推断出顶板中间塑性铰的位置距离简支端0.37处，底板中间塑性铰的位置距离简支端0.75处，与利用本文提出的扩展拉力场理论中塑性铰求解式(2)计算得到的的0.36及0.77相比，结果较为吻合，说明了拉力场理论可以扩展到不考虑屈曲后强度的钢板梁抗剪中。

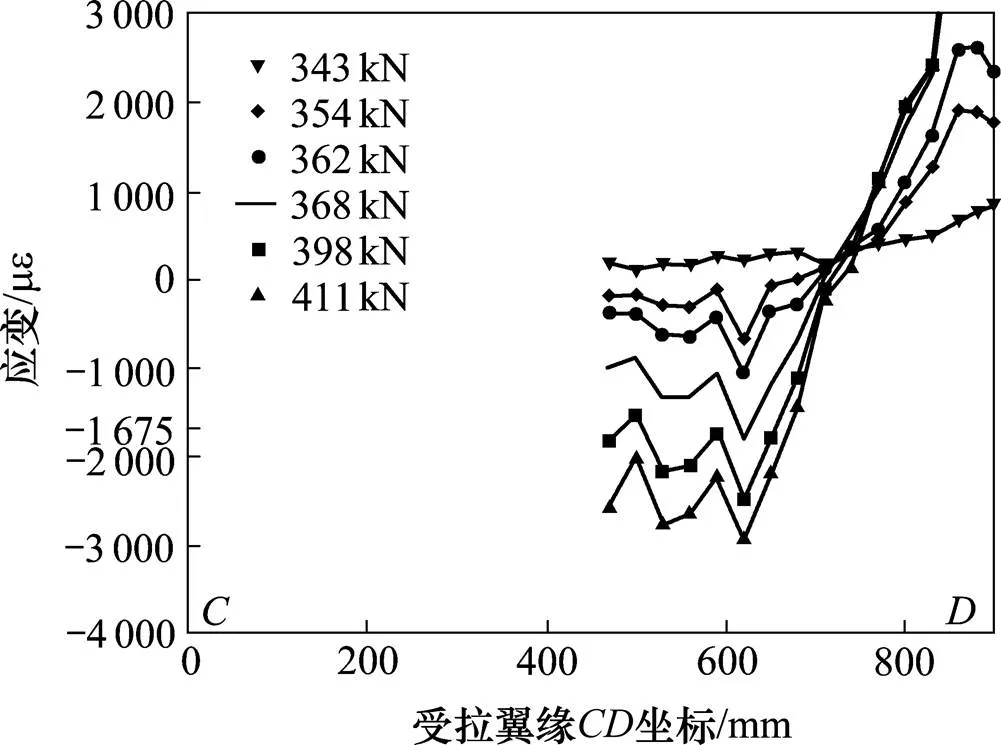
图13 受拉翼缘应变-位置曲线

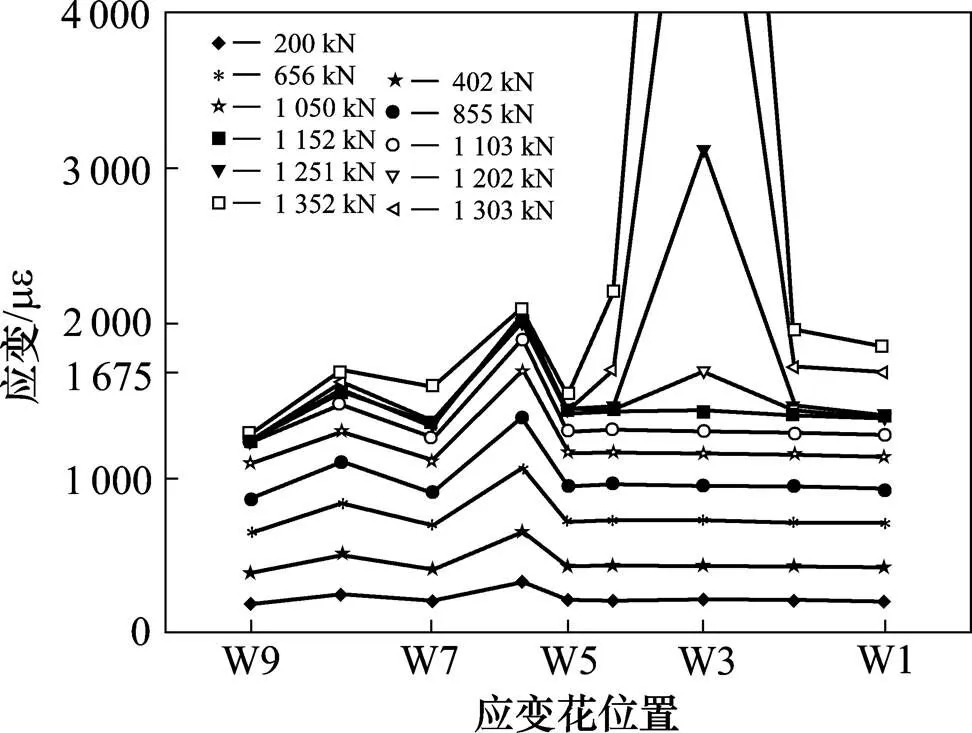
图14 腹板主拉应变-位置曲线

②顶、底板应变

图15～16展示了简支梁顶板、底板的弯曲应变图。由图可以看出，达到极限荷载时，顶板之间的塑性铰形成于距离简支端0.11处，底板之间的塑性铰形成于距离简支端0. 78处，与本文提出的扩展拉力场理论计算以及腹板应变推测的塑性铰位置相差不大，进一步说明了本文提出的扩展拉力场理论的正确性。

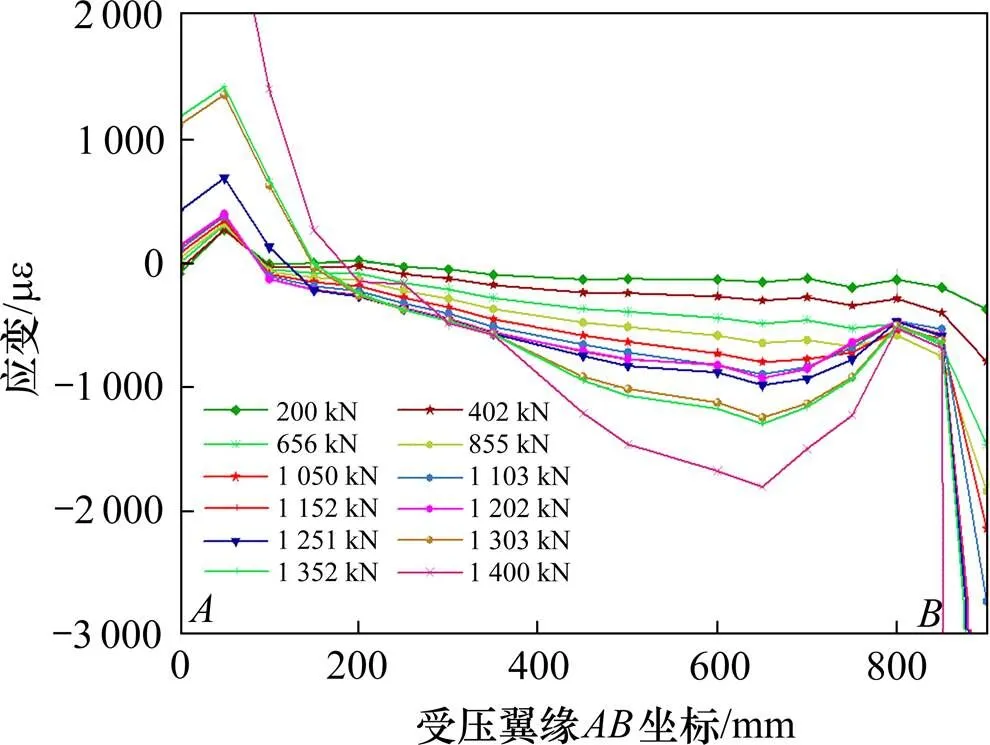
图15 受压翼缘应变-位置曲线

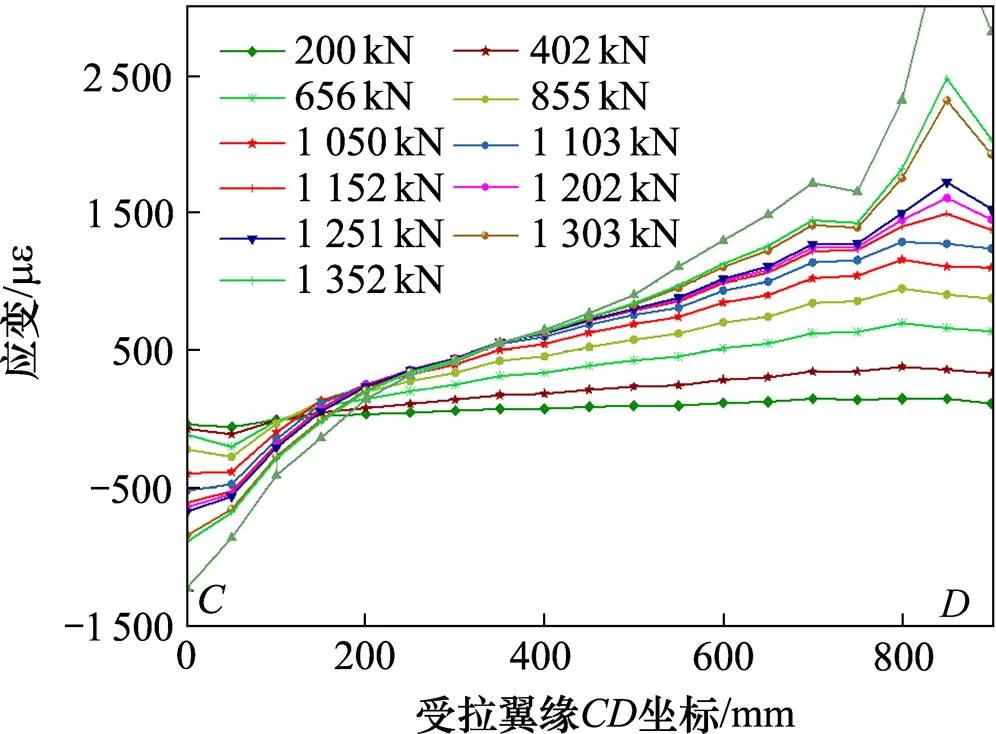
图16 受拉翼缘应变-位置曲线

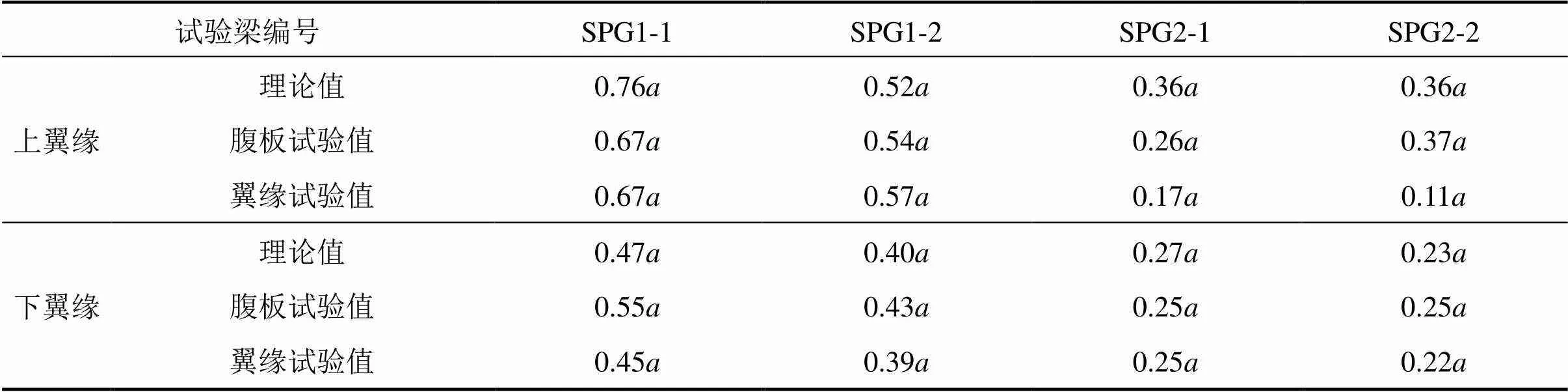
表2 试验梁翼缘塑性铰距离

2.3.4 塑性铰位置

分别采用Rockey拉力场理论与本文扩展拉力场理论中塑性铰求解公式求得发生与不发生腹板剪切屈曲的试验梁翼缘塑性铰位置，将理论值与通过腹板主拉应变试验值和翼缘应变试验值获得翼缘塑性铰之间的距离列于表2，对比结果表明：试验值与理论值吻合良好，验证了本文理论的准 确性。

3 仿真分析

3.1 Abaqus分析模型

本文采用ABAQUS软件建立各试验梁的非线性有限元模型，采用实体单元C3D8R模拟，单元尺寸控制在20 mm，材料参数同前，采用简支边界，如图17所示。

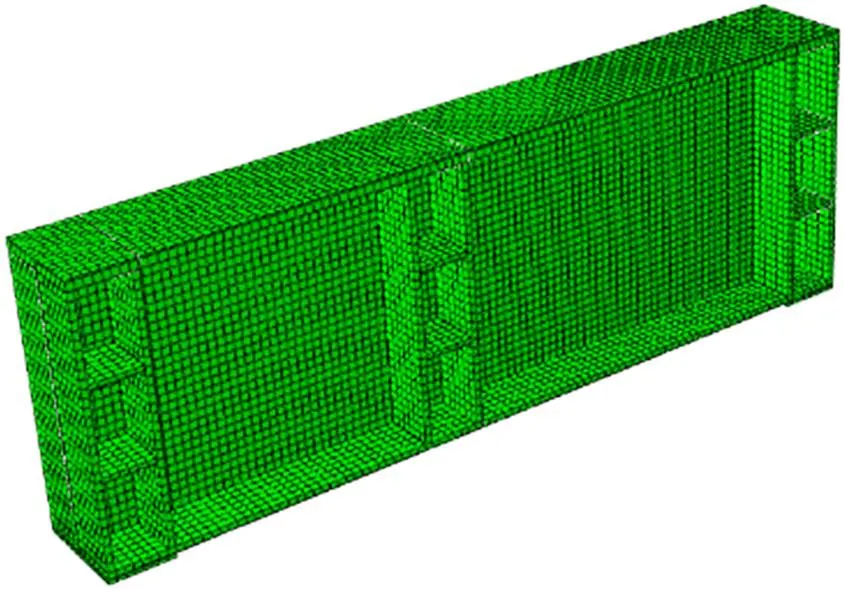
图17 有限元模型网格图

3.2 模型结果

图18～19展示了仿真分析得到的MIises等效应力云图。当试验梁达到极限状态时，腹板在一定宽度内失效，并在上、下翼缘处产生了塑性铰。

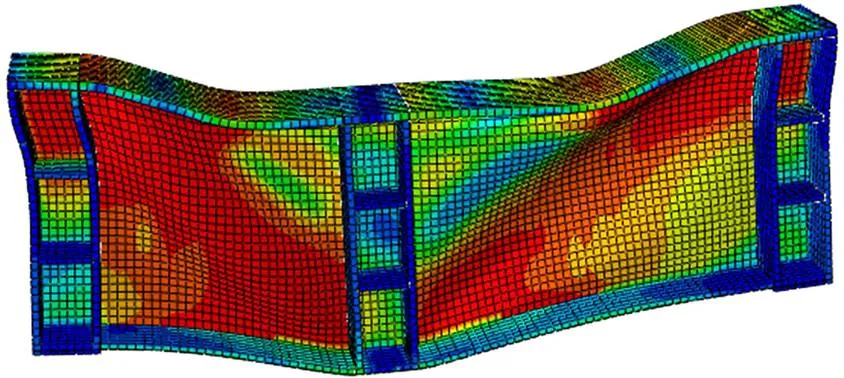
图18 SPG1 MIises等效应力云图

3.3 结果对比

图20为4次试验梁有限元结果与试验结果的荷载-位移曲线对比。

可以看出，试验梁有限元模型与试验结果的起始刚度、极限强度吻合较好，误差较小，本文有限元模型能有效地模拟钢板梁的受剪过程。

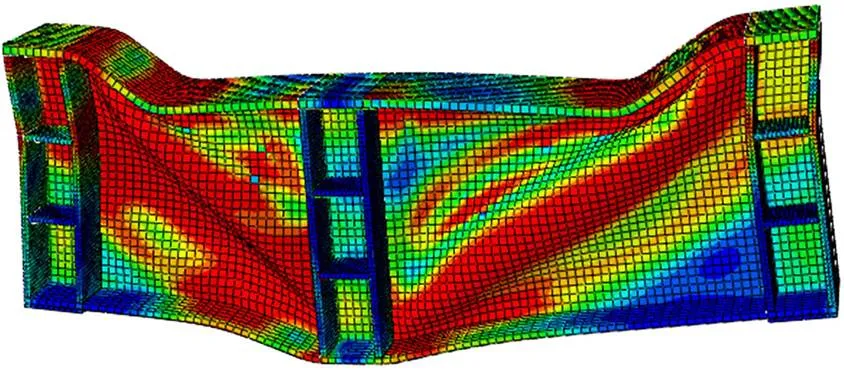
图19 SPG2 MIises等效应力云图

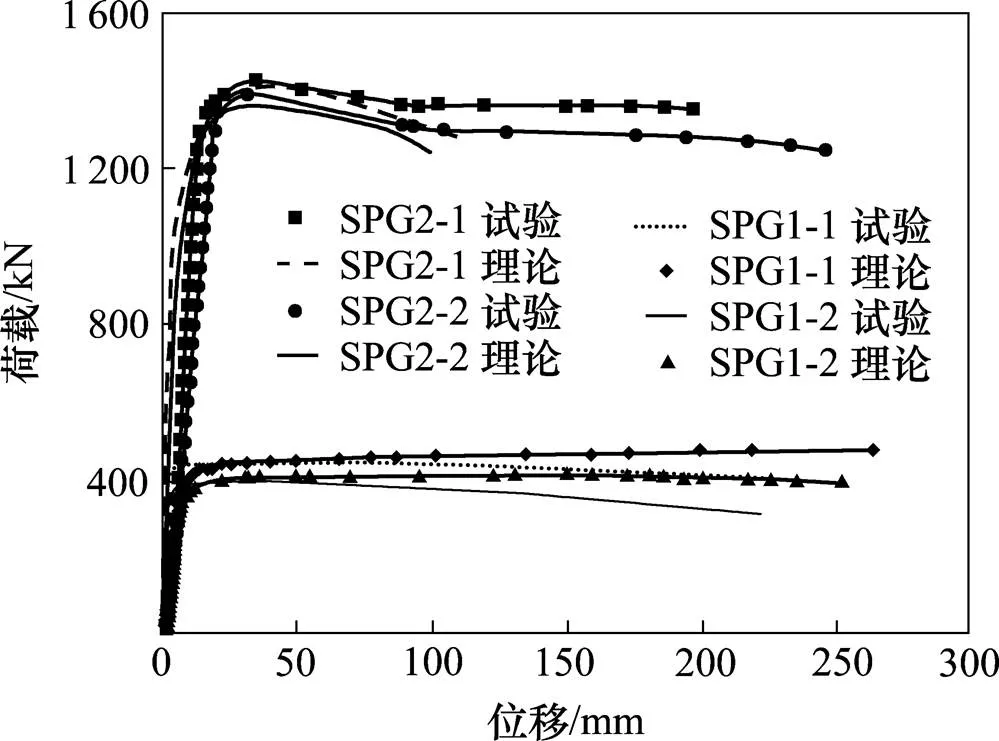
图20 有限元和试验荷载-位移曲线对比

4 拉力场公式验证与适用性讨论

本文将4个试验梁的抗剪试验值test，仿真值abq，按照各规范规定计算的抗剪值以及本文扩展后的拉力场理论值进行对比，列于表3。

1) 对腹板发生弹性剪切屈曲的钢板梁，SPG1-1考虑屈曲后强度的拉力场理论值与试验、仿真结果的比值分别为0.985和1.06，而SPG1-2的比值分别为0.912和0.954，精度较高；规范值则与试验、仿真值相差很大，说明对于发生弹性剪切屈曲的钢板梁，应考虑屈曲后强度的影响。

2) 对于腹板不发生弹性剪切屈曲的钢板梁，SPG2-1采用本文扩展拉力场理论的计算结果与其试验、仿真结果的比值分别为0.958和0.972，而SPG2-2的比值分别为0.95和0.972，精度较高；规范值则与试验值、仿真值相差很大，说明本文提出的扩展拉力场理论适用于腹板不发生剪切屈曲的钢板梁抗剪计算。

EC3 1-5规范采用的是Davies修正的简单屈曲后方法，虽然结果与4片梁的试验值、仿真结果均吻合的较好，但对于腹板发生剪切屈曲的钢板梁，Davies修正未充分考虑屈曲后强度的影响，无论腹板是否发生屈曲，Davies修正均通过试验结果得出的经验公式在腹板抗剪的基础上进行了翼缘抗剪的修正，其准确性还有待讨论。

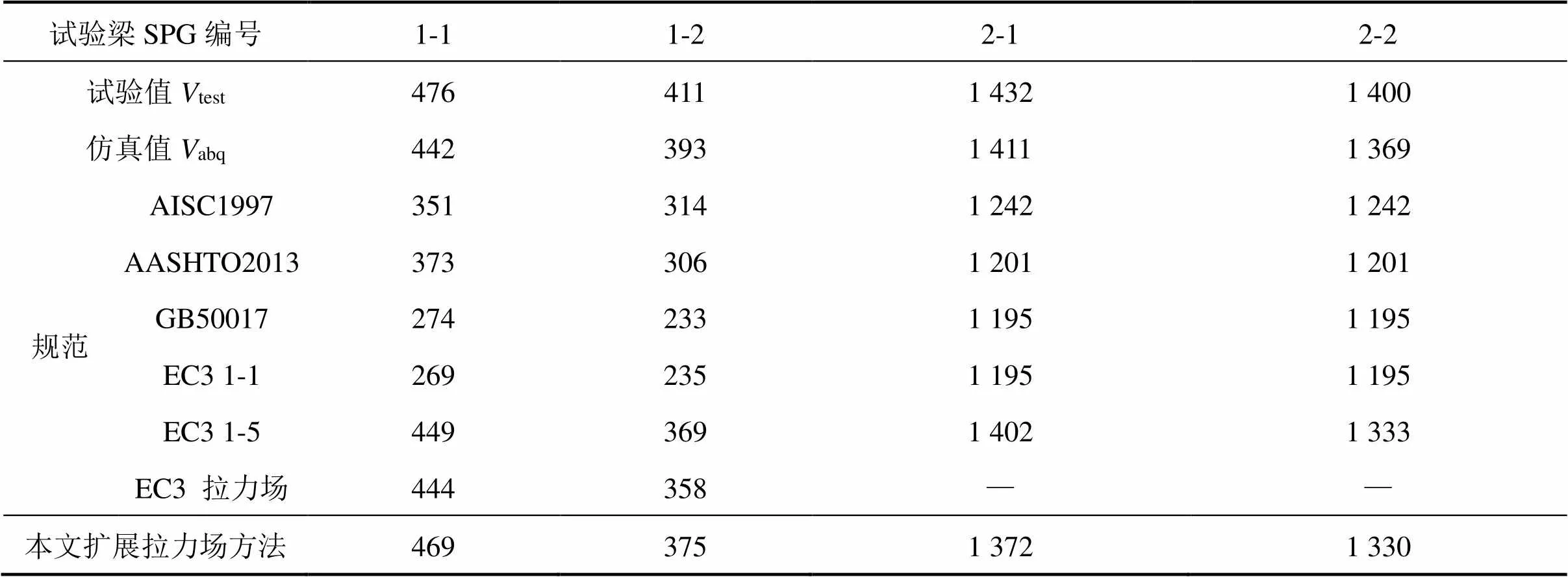
表3 试验梁试验、理论与仿真结果对比

5 结论

1) 对于腹板发生弹性剪切屈曲的钢板梁，利用考虑屈曲后强度的抗剪计算方法较为合理，拉力场理论计算具有较高的精度。

2) 本文提出的扩展拉力场理论，预测剪切荷载作用下腹板不发生弹性剪切屈曲的钢板梁的抗剪承载能力具有较高的精度，可为工程设计及规范修订提供参考。

关于考虑钢板梁腹板残余应力、几何初始缺陷以及翼缘约束作用对抗剪破坏模式及极限承载力的影响有待于进一步研究。

注释

，h，t=腹板长度、高度、厚度；

b，t=翼缘宽度、厚度

τ=腹板剪切屈服应力

σ=腹板屈服应力

V=钢板梁抗剪极限承载力

=翼缘塑性铰之间的距离

c，c=受压、受拉翼缘塑性铰间距

=拉伸膜应力的倾角

M=翼缘的塑性极限弯矩，定义为；

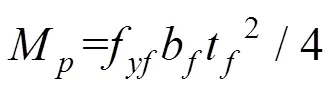
M，M=受压、拉翼缘塑性极限弯矩

[1] Höglund T. Shear buckling resistance of steel and aluminium plate girders[J]. Thin-Walled Structures, 1997, 29: 13-30.

[2] Basler K. Strength of plate girders in shear[J]. Journal of Structure Division, 1961, 87(7): 151-180.

[3] Porter D M, Rockey K C, Evans H R. The collapse behaviour of plate girders loaded in shear[J]. The Structural Engineer, 1975, 53(8): 313-325.

[4] 段兰, 王春生, 王世超, 等. 高强度工字钢梁腹板抗剪性能试验[J]. 中国公路学报, 2017, 30(3): 65-71. DUAN Lan, WANG Chunsheng, WANG Shichao, et al. Web shear behavior test for high strength I steel girders[J]. China Journal of Highway and Transport, 2017, 30(3): 65-71.

[5] 童根树, 任涛. 工字梁的抗剪极限承载力[J]. 土木工程学报, 2006(8): 57-64. TONG Genshu, REN Tao. Shear resistance of slender webs in I-girders[J]. China Civil Engineering Journal, 2006(8): 57-64.

[6] 康孝先, 强士中. 工字梁腹板拉力场理论的修正[J]. 西南交通大学学报, 2008(1): 77-81. KANG Xiaoxian, QIANG Shizhong. Modification of tension field theory on I-girder Web[J]. Journal of Southwest Jiaotong University, 2008(1): 77-81.

[7] Davies A W, Griffith D S C. Shear strength of steel plate girders[J]. Instn Civ Engrs Structs & Bldgs, 1999(134): 147-157.

[8] Alinia M M, Shakiba M, Habashi H R. Shear failure characteristics of steel plate girders[J]. Thin-Walled Structures, 2009, 147(12): 1498-1506.

[9] Hayatdavoodi A, Shanmugam N E. Web buckling and ultimate strength of composite plate girders subjected to shear and bending[J]. International Journal of Structural Stability and Dynamics, 2015, 15(2): 1-18.

[10] Ricky L, Singh K D. Structural performance of hybrid stainless steel plate girders under shear[J]. Thin-Walled Structures, 2019, 143: 1-17.

[11] BS EN 1993-01-05: 2006. Eurocode 3: Design of steel structures-Part 1-5: Plated structural elements[S].

[12] GB 50017—2017, 钢结构设计标准[S]. GB 50017—2017, Standard for design of steel structures[S].

Calculation of shear capacity of steel plate girder considering tension field

LI Lifeng1, 2, GUO Yanyan1, CHENG Zihan1, SUN Jingkai3

(1. College of Civil Engineering, Hunan University, Changsha 410082, China; 2. Key Laboratory for Wind and Bridge Engineering of Hunan Province, Changsha 410082, China;3. Yunnan Wuruoxun Expressway Co., Ltd., Kunming 650000, China)

In order to analyze the reliability of calculating the shear capacity of plate girders with elastic shear buckling of web by tensile field, and to propose the calculation method of the shear capacity of plate girders without elastic shear buckling of web, four shear model tests of steel plate beam were designed and completed in this paper, and the shear failure mode and failure characteristics were grasped. At the same time, test results such as the bending strain and the in-plane deformation of compression flange and tension flange, the main tensile strain and the out of plane deformation of the web were obtained. Based on the experimental phenomena, this paper proposed an extended theory based on Rockey’s theory, which was suitable for calculating the shear capacity of plate girders with elastic shear buckling of web, and the corresponding calculation formula was put forward. At the same time, ABAQUS was used to establish the spatial finite element model of the test girder, and the theoretical and simulation results were in good agreement with the test results. The results are as follows. For plate girders with elastics hear buckling of web, the accuracy of shear capacity calculated by Rockey’s theory is high. And for plate girders without elastic shear buckling of web, the tensile field is also developed in shear failure. In this case, the results of the extended tensile field theory proposed in this paper have high accuracy, which provide some reference value for engineering and specifications.

plate girder; tension field theory; rotation stress field theory; post buckling strength; shear capacity

U448.212

A

1672 - 7029(2020)11 - 2873 - 09

10.19713/j.cnki.43-1423/u.T20191196

2019-12-31

国家自然科学基金资助项目(51978257)；陕西省交通厅科研课题(17-19K)；云南省交通厅科研课题资助项目(2017-17)

李立峰(1971-)，男，湖南沅江人，教授，博士，从事桥梁抗震、超高性能混凝土应用、钢桥与钢混组合桥基本理论等研究；E-mail： lilifeng@hnu.edu.cn

(编辑 涂鹏)