考虑桥墩实测刚度的墩梁固结桥梁合龙顶推力调整简化算法

渠述锋，孟栋梁，杨孟刚

考虑桥墩实测刚度的墩梁固结桥梁合龙顶推力调整简化算法

渠述锋1，孟栋梁2，杨孟刚2

(1. 济青高速铁路有限公司，山东 济南 250014；2. 中南大学 土木工程学院，湖南 长沙 410075)

当墩梁固结桥梁存在合龙温差时，为使桥梁结构的成桥状态接近于设计基准状态，需要对合龙顶推力进行调整，且当地质状况复杂时，有限元软件难以对桩-土相互作用进行精确的模拟，因此有必要考虑顶推过程中桥墩实测抗推刚度的影响。以某塔墩梁固结矮塔斜拉桥为工程背景，提出一种根据合龙温差和桥墩实测抗推刚度，在顶推过程中调整合龙顶推力的简化计算方法。研究结果表明：合龙温差会使实际成桥状态偏离设计基准状态，该偏差在顶推前可以通过对合龙顶推力进行调整来抵消；桥墩实测抗推刚度会对合龙顶推力的调整产生一定的影响，需在顶推过程中根据实测值进一步调整合龙顶推力来消除；提出的简化算法可方便快速应用于同类型桥梁顶推过程中合龙顶推力的精确调控。

墩梁固结桥梁；合龙温差；桥墩实测抗推刚度；顶推力调整；简化算法

塔墩梁固结矮塔斜拉桥是介于刚构桥和常规斜拉桥之间的桥型。成桥之后混凝土的收缩徐变作用会使主梁线形下挠且会产生较大的二次内 力[1-3]；为了减小成桥后收缩徐变等因素对后期结构状态的影响，在其合龙时需对梁体施加纵向水平顶推力，使合龙前各桥梁参数产生一定的反向预偏量，以抵消收缩徐变等引起的结构位移和二次内力。对于合龙顶推力的计算分析已有一些学者进行了研究[4-5]。李军等[6]对某大跨连续刚构桥的顶推力及顶推位移分析表明：顶推施工能改善桥墩长期受力状态，避免桥墩墩底出现拉应力，配合预拱度设置，可以有效解决跨中下挠的病害；李杰等[7]通过数值计算分析得出顶推力与成桥后主梁的水平位移呈线性变化；石雪飞等[8]用顶推力与位移双控措施来控制V形墩刚构桥的“墩底辅助顶推”，保证成桥线形和内力同时达到设计要求；白玉堂等[9]通过计算得出了不同顶推力与Y形桥墩墩底截面弯矩的关系；杨孟刚等[10]为确定合龙顶推力的合理取值范围，基于《公路钢筋混凝土及预应力混凝土桥涵设计规范》中的裂缝宽度公式，从控制桥墩裂缝宽度的角度出发推导出了合龙顶推力简化计算方法。目前，对于部分斜拉桥合龙顶推力的研究仍不完善[11-12]。实际桥梁合龙时通常存在合龙温差(即实际合龙温度与设计合龙温度不一致)，会导致合龙后主梁产生偏离设计状态的伸缩变形，将影响主梁线形及成桥内力[13]。另一方面，仿真计算模型中常采用m法模拟桩-土相互作用，桥墩的计算抗推刚度往往与实际抗推刚度存在一定的偏差[14]。目前，关于合龙温差对合龙顶推力影响的研究通常未考虑桥墩(桥墩+桩基础)实际抗推刚度的影响，且缺乏在顶推过程中快速调整合龙顶推力的简化计算方法。论文以某塔墩梁固结矮塔斜拉桥为例，在充分考虑合龙温差和桥墩实测抗推刚度的基础上，提出了一种调整合龙顶推力的简化算法，可实现对合龙顶推力快速精确的调整，且在调整过程中不再需要复杂的有限元计算分析。

1 背景工程及有限元模型

以某三塔四跨塔墩梁固结矮塔斜拉桥为工程背景，桥跨布置为(140+2×225+120) m；中塔高45 m，边塔高35 m；全桥共108根φS15.2钢绞线斜拉索，单索面双排布置。主梁为预应力混凝土结构，截面形式为变高度斜腹板单箱三室，顶板宽36 m，跨中梁高3.8 m，主塔根部梁高6.8 m。桥墩为双肢薄壁空心桥墩，两肢间净距为2 m。主梁采用悬臂施工，先合龙中跨，再合龙边跨。

采用空间有限元软件Midas/Civil建立全桥有限元模型，如图1所示。主梁、主塔、桥墩、承台、桩基均采用梁单元模拟，拉索采用索单元模拟，全桥共划分为2 110个单元，2 087个节点。边墩采用竖向支撑模拟，桩基底部边界条件按固结处理，桩基与土层的相互作用采用一般支撑模拟，刚度根据土层地质状况按m法计算所得。主梁采用“T”形悬臂施工，共分26个梁段，施工周期按3 a考虑，收缩徐变达到终极值按运营2 000 d考虑，后文的成桥状态均表示已完成收缩徐变。

图1 Midas有限元模型

2 合龙顶推力调整有限元方法

2.1 成桥状态对合龙温差的敏感性分析

为研究合龙温差对成桥状态的影响，以设计合龙温度20 ℃，设计顶推力14 000 kN为基准状态；分别建立合龙温差为±15 ℃的有限元模型以确定成桥以后主梁线形、梁顶应力、拉索索力、塔顶偏位、墩顶位移、墩底应力等参数相较于基准状态的偏差并分析这些参数对合龙温差的敏感程度，分析结果如图2所示。

(a) 梁顶应力；(b) 拉索索力；(c) 墩底应力；(d) 主梁线形；(e) 塔顶偏位；(f) 墩顶位移

由图2(a)和2(b)可知，梁顶应力及拉索索力受合龙温度的影响较小，索力偏差在-1.26%～1.16%之间、梁顶应力偏差在-8.65%～8.65%之间，但是由图2(c)可知，合龙温差对墩底应力有较大的影响。这主要是因为合龙温差使主塔、桥墩、主梁及拉索均产生膨胀或收缩，拉索可以认为是无约束自由膨胀收缩，索力变化很小；主梁在顺桥向伸缩时因为有桥墩的约束，会对梁顶应力产生一定的影响；主梁的伸缩变形会使桥墩产生侧移，因此会对墩底的应力产生较大的影响。由图2(d)～2(f)可以看出，由于桥梁结构近似关于8号墩对称，所以8号墩所对应的主梁线形、塔顶偏位及墩顶位移受合龙温差的影响较小，7号和9号墩由于合龙温差的作用会发生侧移，对应的主梁线形、塔顶偏位及墩顶及墩顶位移受合龙温差的影响较大。因此，在合龙阶段存在合龙温差时，应重点关注合龙温差对主梁线形、塔顶偏位、墩顶位移及墩底应力的影响。

2.2 合龙顶推力调整

根据第2.1节分析结果，以设计成桥状态作为基准状态，选择跨中恒载挠度、塔顶偏位、墩顶位移、墩底外侧纤维应力等相对于基准状态的偏差值为控制参数，分析了各成桥状态控制参数偏差值随合龙温度及合龙顶推力的变化规律，如图3所示。限于篇幅，图3中只给出左半桥各控制参数变化规律。由图3可知，各控制参数随合龙温度及合龙顶推力的增加基本呈线性变化，且两者变化的斜率相反，即可以认为由合龙温差产生的各项控制参数相对于基准状态的偏差是可以通过调整合龙顶推力来抵消的；图3中各图的交点即为设计基准状态，对应的合龙顶推力为14 000 kN，合龙温度为20 ℃。

(a) 7～8号墩跨中恒载挠度；(b) 7号塔塔顶偏位；(c) 7号墩墩顶位移；(d) 7号墩右肢墩底应力

以各控制参数达到设计基准状态为控制目标，合龙顶推力调整可按下式计算：

式中：t为控制参数随合龙温度变化率；F为控制参数随合龙顶推力变化率；Δ为设计合龙温度与实际合龙温度之差；Δ为设计合龙顶推力与实际顶推力之差，即顶推力折减值。

实桥合龙时，通过从气象部门获取资料及现场温度的监测，最终确定在合龙锁定时的温度为11 ℃，即Δ=9 ℃。根据式(1)，该桥7～8号墩、8～9号墩间合龙顶推力调整计算过程分别见表1和表2。由表1和表2可知：①各项控制参数随合龙顶推力与合龙温度的变化率是不同的，说明不能通过调整合龙顶推力使各项控制参数均达到设计成桥状态，可以取各项控制参数顶推力调整的平均值作为最终的顶推力调整量；②经计算得到7～8号墩间的顶推力平均折减6 264 kN，8～9号墩间的顶推力平均折减5 430 kN，这是由于9号墩相较于7号墩的桩基更长，桥墩及桩基的抗推刚度较小的缘故；③通过对比可以发现，各项控制参数顶推力折减的平均值与按墩顶位移计算的折减量较为接近，在合龙顶推力调整时可以近似选取墩顶位移作为控制参数[12, 15]。

表1 7～8号墩间合龙顶推力调整

表2 8～9号墩间合龙顶推力调整

3 顶推过程中的合龙顶推力调整简化算法

第2节介绍的方法需要计算大量的有限元模型，且通过有限元模拟桩-土之间的相互作用通常具有一定的误差。实际上，在墩梁固结桥梁中跨合龙前，需要对预定的合龙顶推力进行分级顶推；在进行前几级顶推时通过测量相邻桥墩墩顶相对位移，即可获得桥墩的实测相对抗推刚度(假定顶推力与墩顶相对位移呈线性关系)，可以实现对合龙顶推力进一步精确调整。正是基于此，本文提出了一种在顶推过程中调整合龙顶推力的简化计算方法。

3.1 简化算法

3.1.1 成桥后由合龙温差产生的墩顶相对位移

选择实测较为方便的墩顶相对位移作为合龙控制参数(第2节已对其可行性进行了说明)。合龙温差对于结构的作用相当于整体升降温，由第2节分析结果可知，整体升降温对索力的影响较小，因此可以忽略索力变化的影响；且主塔及拉索结构对由合龙温差产生的墩顶相对位移的影响也可以忽略。因此，选择的简化结构如图4(a)所示，选取一半结构建立基本体系，如图4(b)所示，基本体系中用轴向力N，弯矩代替跨中对称约束。需要说明的是，对于非对称结构同样可解，本文为方面描述，选择的简化模型为对称结构。

(a) 简化结构；(b) 基本体系

为求解赘余力N，，建立力法典型方程：

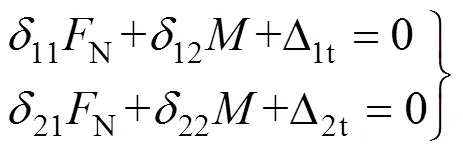
式中：11，12=21，22为在基本体系上，第2个角标对应的单位力引起的第1个角标对应的位移，即柔度系数，可用图乘法求解(角标1和2分别代表N和)；Δ1t和Δ2t为在基本体系上由温度引起的对应于N和的位移。

由式(2)解得：

式中：Δ为设计合龙温度与实际合龙温度之差；为混凝土线膨胀系数；为主梁长度；为桥墩高度；为主梁混凝土弹性模量；为主梁横截面积，对于变截面梁可近似取主梁各特征截面积的平均值；1、2为主梁及桥墩的截面惯性矩。对于式3(a)，令：

则式3(a)可写成：

式中：相当于由桥墩产生的抵抗由合龙温差引起的墩顶相对位移的刚度，即两桥墩的相对抗推 刚度。

在求解出赘余力N和后，即可求出墩顶相对侧移Δ：

式中：Δ为由合龙温差产生的墩顶相对位移；Δt，Δk分别为在基本体系上由合龙温差、赘余力引起的墩顶相对位移。

由式(6)可以看出，由合龙温差产生的墩顶的相对位移包括2部分：1) 自由效应：合龙温差产生的主梁自由伸缩作用；2) 约束效应：温度力(由桥墩的约束作用导致)引起的主梁伸缩效应。将式(5)代入式(6)有：

3.1.2 合龙顶推力调整

由以上的计算过程可知，采用简化算法后，只需计算式(8)～(10)就可以同时考虑合龙温差及实测桥墩抗推刚度，对合龙顶推力进行快速精确调整。简化算法计算流程如图5所示。

3.2 实桥验证

3.2.1 实桥顶推力简化计算

前述矮塔斜拉桥的设计基准状态为合龙温度20 ℃，顶推力14 000 kN，Δ=9 ℃。在合龙顶推前，仅考虑合龙温差作用，按照第2.2节方法计算出预定合龙顶推力；考虑到顶推施工的方便，7～8号墩、8～9号墩间合龙顶推力的预定值均取为8 000 kN。预定合龙顶推力分5级加载，每级顶推力为 1 600 kN。

图5 顶推过程简化算法流程

2) 计算由合龙温差产生的变形Δ。

按式(8)计算由温差产生的变形，其中= 0.000 01 ℃；Δ9 ℃；=225 m；=3.60×104MPa；=33.779 m2。计算结果如表4所示。为验证式(8)的正确性，表中同时给出了有限元模型的计算结果。由表4可知，按简化方法计算Δ的结果具有很高的精度，验证了简化算法的可行性。

3) 合龙顶推力调整。

由上一步可知，由实际合龙温度变化到设计基准温度，7号和9号墩会分别相对于8号墩向外侧移18.94 mm和19.12 mm。因此可以在顶推阶段通过减小合龙顶推力预先消除由合龙温差产生的7号、9号墩相对于8号墩的侧移，使得最终的成桥状态接近设计成桥状态。将Δ1=18.94 mm，Δ2=19.12 mm分别代入式(9)，计算得7～8号墩间需折减顶推力Δ2=6 621 kN，8～9号墩间需折减顶推力Δ25 778 kN。进一步由式(10)计算可得7～8号墩、 8～9号墩间的最终合龙顶推力分别为7 379 kN、 8 222 kN。

表3 合龙顶推阶段墩顶相对位移实测值

注：墩顶侧移值为10个测点的平均值。

表4 合龙温差引起的墩顶相对位移

注：有限元模型中桥墩刚度修改为桥墩实测抗推刚度。

3.2.2 对比分析

合龙顶推力调整有限元方法与简化算法计算结果对比见表5，表中的计算结果均以墩顶位移作为控制参数。由表5可知：1) 当仅考虑合龙温差作用时，通过有限元计算与采用简化算法(桥墩抗推刚度从有限元模型中提取)计算的合龙顶推力折减值的误差分别为-1.81%和-1.45%，2种方法的计算结果非常接近，验证了简化算法的正确性；2) 考虑合龙温差及桥墩实测抗推刚度的简化计算结果相较于仅考虑合龙温差的有限元计算结果的偏差分别为8.13%和7.14%，说明桥墩实际抗推刚度对调整合龙顶推力的影响是不可忽略的，且地质状况越复杂有限元模拟的偏差越大。终上所述，在顶推合龙时需同时考虑合龙温差及桥墩实测抗推刚度对合龙顶推力进行调整。

表5 计算结果对比

4 结论

1) 合龙温差对成桥状态有显著的影响，由于合龙温差产生的成桥控制参数相对设计成桥状态的偏差，是可以通过调整合龙顶推力来消除的；但在计算合龙顶推力的调整值时，有必要考虑桥墩实际抗推刚度影响，尤其是对于存在地质状况复杂等因素导致的有限元难以准确模拟桥墩及桩基实际抗推刚度的情况。

2) 提出了一种考虑合龙温差及桥墩实测抗推刚度的墩梁固结体系桥梁合龙顶推力调整的简化算法，该算法先通过有限元计算仅考虑合龙温差作用下合龙顶推力的调整值，从而确定预定的合龙顶推力，在对预定的合龙顶推力进行分级顶推时，根据桥墩实测抗推刚度进一步对合龙顶推力进行精确调整。

3) 本文提出的调整合龙顶推力的该简化计算方法可实现对墩梁固结体系桥梁合龙顶推力快速精确的调整，在有限元难以准确模拟桥墩及桩基实际抗推刚度时，该方法尤为适用；且在调整过程中不再需要复杂的有限元计算分析。

[1] 孟新奇, 魏伦华, 张津辰, 等. 大跨径刚构桥梁跨中下挠问题研究[J]. 世界桥梁, 2013, 41(2): 76-79. MENG Xinqi, WEI Lunhua, ZHANG Jinchen, et al. Study of down warping in the mid-span of long-span rigid frame bridge[J]. World Bridges, 2013, 41(2): 76-79.

[2] LI W, LIU H. Calculating the closure jacking-force of a large-span pre-stressed concrete continuous rigid frame bridge[J]. International Journal of Engineering Research and Applications, 2015, 5(4): 29-32.

[3] 陈淮, 陈鹏飞, 李杰. 刚构-连续组合梁桥主梁合龙关键技术[J]. 铁道科学与工程学报, 2015, 12(1): 113-118. CHEN Huai, CHEN Pengfei, LI Jie. Study on key technology of the main girder closure of rigid frame-continuous combination beam bridge[J]. Journal of Railway Science and Engineering, 2015, 12(1): 113-118.

[4] 伍英, 刘榕, 邹卓, 等. 多塔矮塔斜拉桥合龙顶推力多目标优化研究[J]. 铁道科学与工程学报, 2018, 15(6): 1481-1486. WU Ying, LIU Rong, ZOU Zhuo, et al. Closure jacking force of multi-objective optimization of multi-span extradosed cable-stayed bridge[J]. Journal of Railway Science and Engineering, 2018, 15(6): 1481-1486.

[5] 易锦, 贺国京, 陆杰, 等. 合龙及体系转换顺序对多跨刚构-连续组合梁桥影响分析[J]. 铁道科学与工程学报, 2013, 10(5): 27-31. YI Jin, HE Guojing, LU Jie, et al. Impact analysis of closure order and system transformation order for bridges with rigid frame-combined continuous beam[J]. Journal of Railway Science and Engineering, 2013, 10(5): 27-31.

[6] 李军, 曾一帆, 陈辉, 等. 大跨径连续刚构桥中跨合龙顶推力研究[J]. 铁道科学与工程学报, 2015, 12(2): 335-341. LI Jun, ZENG Yifan, CHEN Hui, et al. Study on mid-span jacking force for long span continuous rigid- frame bridges[J]. Journal of Railway Science and Engineering, 2015, 12(2): 335-341.

[7] 李杰, 陈彬. 连续刚构桥顶推力计算与优化分析[J]. 郑州大学学报(工学版), 2013, 34(6): 85-89. LI Jie, CHEN Bin. Analysis of continuous rigid frame bridge jacking force calculation and optimization[J]. Journal of Zhengzhou University (Engineering Science), 2013, 34(6): 85-89.

[8] 石雪飞, 朱荣, 阮欣. V形墩刚构桥墩底顶推合龙施工控制[J]. 桥梁建设, 2015, 45(2): 105-109. SHI Xuefei, ZHU Rong, RUAN Xin. Construction control of closure of V-shape pier rigid-frame bridge aided by jacking at pier footings[J]. Bridge Construction, 2015, 45(2): 105-109.

[9] 白玉堂, 胡云耀. Y形墩刚构桥合龙顶推力设计探讨[J]. 中外公路, 2015, 35(3): 185-187. BAI Yutang, HU Yunyao. Discussion on design of jacking force for closure of Y-shape pier rigid-frame bridge[J]. Journal of China & Foreign Highway, 2015, 35(3): 185- 187.

[10] 杨孟刚, 黄文龙, 卫康华. 塔墩梁固结矮塔斜拉桥合龙顶推力的简化计算方法[J]. 桥梁建设, 2017, 47(3): 71- 75. YANG Menggang, HUANG Wenlong, WEI Kanghua. Simplified calculation method of jacking force for closure of an extradosed bridge with rigid fixity of pylons, piers and main girder[J]. Bridge Construction, 2017, 47(3): 71-75.

[11] 魏建斌, 魏家乐, 马玲. 高墩大跨连续刚构桥顶推合龙控制技术研究[J]. 世界桥梁, 2014, 42(4): 39-43. WEI Jianbin, WEI Jiale, MA Ling. Study of control techniques for closure of long-span continuous rigid- frame bridge with high-rise piers by pushing[J]. World Bridges, 2014, 42(4): 39-43.

[12] 严宗学, 王凌波, 卢旭, 等. 合龙温差下部分斜拉桥顶推力的确定[J]. 土木工程与管理学报, 2016, 33(2), 51- 55. YAN Zongxue, WANG Lingbo, LU Xu, et al. Determination of jacking-force of extradosed bridge considering final closure temperature differences[J]. Journal of Civil Engineering and Management, 2016, 33(2): 51-55.

[13] 谭冬莲, 王学礼, 王飞. 大跨径连续刚构桥多跨同时合龙顶推力优化施工[J]. 施工技术, 2015(44): 332-335. TAN Donglian, WANG Xueli, WANG Fei. The optimizing calculation on closure jacking force of long-span continuous rigid-frame bridge based on same-time closure[J]. Construction Technology, 2015(44): 332-335.

[14] 许明雷, 罗力军. 排调河一号特大桥中跨合龙顶推控制[J]. 桥梁建设, 2011(4): 79-82. XU Minglei, LUO Lijun. Control of push for closure of central span of Paidiao River Bridge No. 1[J]. Bridge Construction, 2017(4): 79-82.

[15] 邹娜, 王政平. m法在桩基计算应用中的误差分析[J]. 港工技术, 2009, 46(6): 26-27. ZOU Na, WANG Zhengping. Error analysis on m-method application in computation of pile foundations[J]. Port Engineering Technology, 2009, 46(6): 26-27.

Simplified calculation method of adjusting jacking force for the closure of pier-girder rigid bridges considering actual measured stiffness of piers

QU Shufeng1, MENG Dongliang2, YANG Menggang2

(1. Jinan-Qingdao High Speed Railway Co., Ltd., Jinan 250014, China; 2. School of Civil Engineering, Central South University, Changsha 410075, China)

To make pier-girder-consolidated bridges close to the design finished state, the jacking force needs to be adjusted when there is a closure temperature difference. Moreover, the finite element method is difficult to simulate the soil-pile interaction accurately due to the complex geological conditions. Therefore, it is necessary to consider the actual measured anti-pushing stiffness of piers in the process of pushing. Taking an extradosed cable-stayed bridge as the engineering background, a simplified calculation method is proposed to adjust the jacking force according to the closure temperature difference and the actual measured anti-pushing rigidity of the piers. The results indicate that the closure temperature difference will cause the actual finished state to deviate from the designed finished state, which can be counteracted by adjusting the jacking force. The actual measured anti-pushing stiffness of piers can influence the adjustment of closure jacking force, and it needs to be further adjusted according to the actual measured values during the process of pushing. The proposed simplified method can be quickly and conveniently applied to the precise control of the jacking force of the same type of bridge during the process of pushing.

pier-girder-consolidated bridges; closure temperature difference; the actual measured anti-pushing stiffness of piers; adjustment of jacking force; simplified calculation method

U448.27；U445.466

A

1672 - 7029(2020)11 - 2864 - 09

10.19713/j.cnki.43-1423/u.T20200678

2020-07-20

山东省交通运输厅科技计划资助项目(2020B79)

杨孟刚(1976-)，男，江西安义人，教授，博士，从事桥梁抗震与设计理论研究；E-mail：mgyang@csu.edu.cn

(编辑 蒋学东)