不等横向联结系对钢-混组合梁桥荷载横向分布的影响研究

李立峰，程子涵，冯威，刘新华

不等横向联结系对钢-混组合梁桥荷载横向分布的影响研究

李立峰1，程子涵1，冯威2，刘新华3

(1. 湖南大学 土木工程学院，湖南 长沙 410082；2. 西安公路研究院，陕西 西安 710065；3. 中交第二公路勘察设计研究院有限公司，湖北 武汉 430056)

目前，中等跨径窄幅钢-混组合梁桥常采用“两片组合梁成榀预制、整体吊装”的施工工艺，榀内横向联结密布、与主梁一起预制，而榀间横向联结在现场安装。为减少现场施工，榀间横向联结设置较少、与榀内横向联结数量不对等。为研究这种布置对桥梁荷载横向分布的影响以及传统理论方法的适用性，结合一座跨径40 m的组合桥，建立空间实体有限元分析模型，选取不同的桥面板厚度情况，以横向联结的数量与刚度为参数进行分析，获得了荷载横向分布影响规律。基于有限元结果，对传统的刚性横梁法、刚接梁法等进行了适用性评价。研究结果表明：榀内横向联结数量足够、榀间仅设置端部和跨中横向联结时，继续增加榀间横向联结对荷载横向分布影响较小，故可仅在梁端和跨中设置榀间横向联结；横向联结的刚度对荷载横向分布影响甚小；传统理论方法获得的荷载横向分布系数均大于有限元结果，偏于安全。

桥梁工程；钢-混组合梁；横向联结系；荷载横向分布；有限元分析

多梁式工字钢-混凝土组合梁桥具有受力明确、方便预制、质量轻、便于吊装、施工快捷等优点，近年来在中等跨径桥梁中得到广泛应用[1-2]。为了保证主梁稳定性和荷载横向传递的需要，梁与梁之间均匀设置钢横撑[3-4]。但目前，施工现场条件和吊装能力合适时，会先将2片组合梁用钢横撑连接(称为“一榀”)，作为一个整体吊装单元架设就位[5]，榀与榀之间再设置适量钢横撑进行连接。为降低现场施工量，榀间设置的钢横撑数量通常少于榀内，需针对这样榀内、榀间横向联结布置数量不一致情况下的荷载横向分布计算进行进一步研究。关于桥梁的荷载横向分布计算，美国AASHTO- LRFD[6]规范给出的计算公式考虑了桥梁跨度、主梁间距、桥面板厚度、主梁抗弯刚度等因素的影响；国内一般采用传统的荷载横向分布计算方法，有杠杆法、刚性横梁法、刚(铰)接梁(板)法等，每种方法均对主梁间的横向连接构造做出基本假定[7]。为考虑横向联结系的作用，Abendroth等[8-11]采用数值分析方法，针对横向联结的形状及布置数量对于主梁荷载横向分布的影响展开了研究。现阶段我国对钢-混组合梁桥的荷载横向分布的相关研究甚少，且上述的传统计算方法及研究是基于榀内外设置等量横向联结系的情况，或直接忽略了横向联结系的影响。对于采用工厂成榀预制、现场按榀吊装的中等跨径组合梁桥，有必要进一步分析其榀内、榀间设置不等横向联结的情况下荷载横向分布的规律。基于此，本文结合一座钢-混凝土组合桥，利用有限元软件ANSYS建立全桥模型，研究不等横向联结系数量和刚度对于宽跨比小于0.5的中等跨径钢-混组合梁桥荷载横向分布的影响；结合空间有限元分析结果，与传统刚性横梁法、刚接梁法等的计算结果进行对比分析，并讨论这些方法的适用性。

1 工程背景

云南省某三孔一联3×40 m钢-混组合梁桥，桥面分幅，单幅宽16.8 m、由6片梁组成，梁高2.08 m，梁间距2.8 m，宽跨比为0.42，截面如图1所示。组合梁的钢结构部分采用Q345焊接工字梁，高1.8 m，桥面板采用C50混凝土，最大厚度为0.28 m。 组合梁采用工厂预制，先利用X形钢横撑将2片钢梁组拼在一起，与预制的混凝土板相接后形成一榀组合梁；将组合梁运至施工现场，整榀梁作为一个吊装单元进行架设，再使用X形钢横撑连接相邻的两榀梁；最后浇筑榀间翼缘板湿接缝。本文将单榀组合梁内的横向联结定义为榀内横撑，两榀组合梁之间的横向联结定义为榀间横撑。

2 有限元分析

桥梁的荷载横向分布特性取决于桥梁的自身结构特性，包括跨径、主梁的截面尺寸以及主梁间的连接方式[12]，除横向联结系外，本文还考虑了不同桥面板刚度对荷载横向分布产生的影响。

分别选取桥面板厚度为200 mm和280 mm 2种情况，采用通用软件ANSYS建立该桥单跨的线弹性三维有限元模型，研究跨中荷载横向分布随榀内与榀间横撑数量和刚度的变化。

2.1 空间有限元模型

钢梁及加劲肋采用壳体单元Shell63模拟，混凝土桥面板采用实体单元Solid65模拟，钢横撑采用梁单元Beam188模拟。混凝土的弹性模量为34.5 GPa，泊松比为0.2；钢材弹性模量为206 GPa，泊松比为0.3。为保证节点自由度不同的单元之间的连接，壳单元与实体单元之间用MPC多点约束进行刚接，梁单元与壳单元之间则用MPC184刚性梁单元进行连接，有限元模型如图3所示。

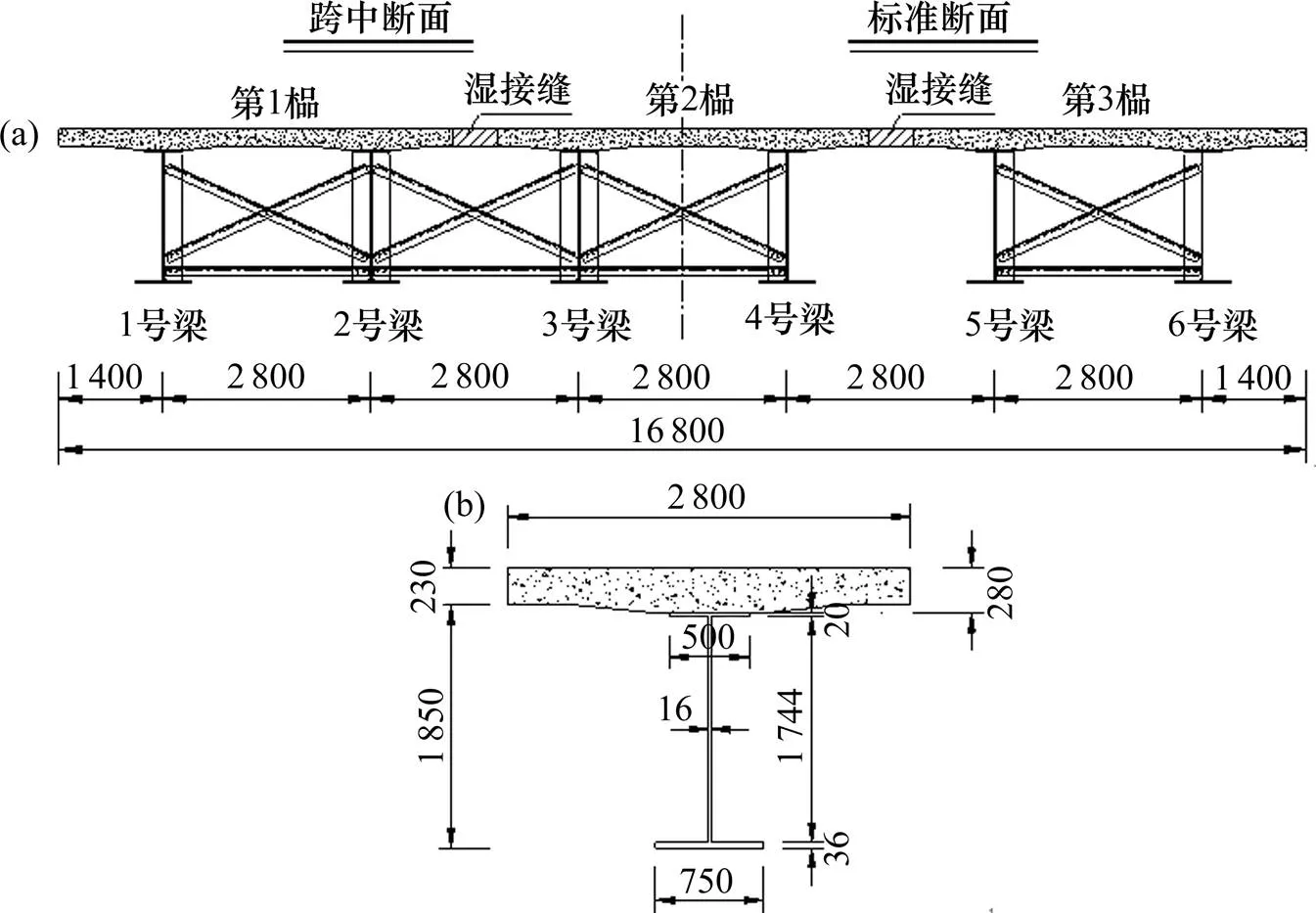
单位：mm

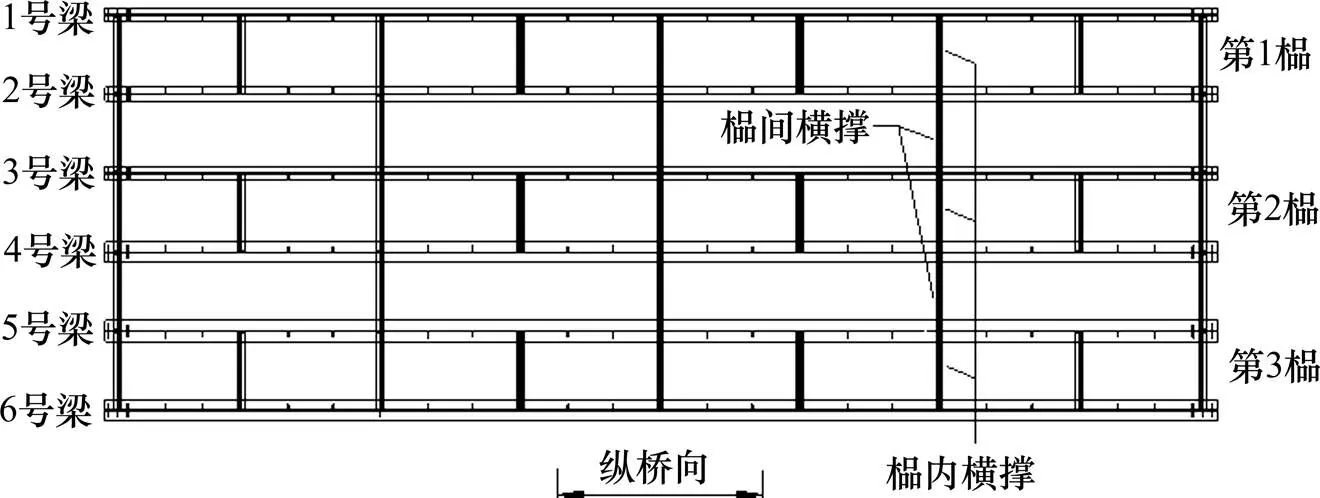
图2 不等横向联结系沿纵向布置

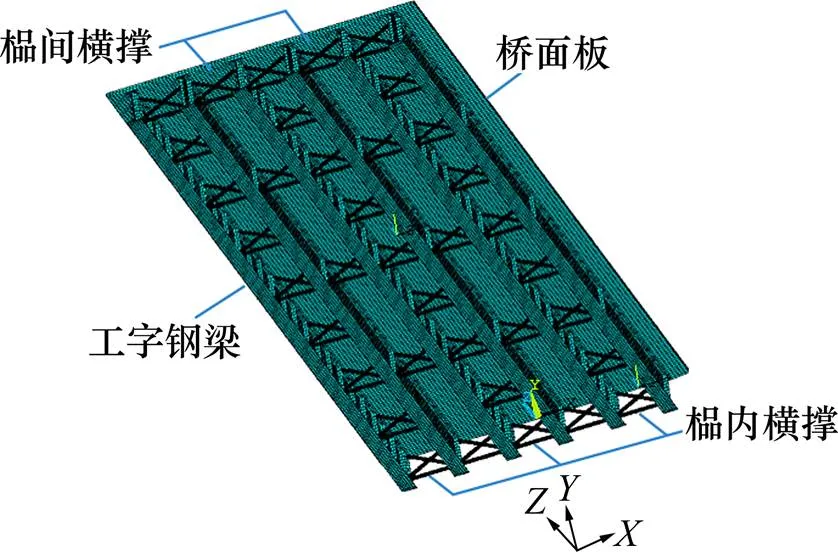
图3 空间有限元模型

2.2 荷载施加方法

对于等截面简支梁桥，在按半波正弦曲线沿桥跨分布的荷载作用下，主梁的挠度分布、内力分布和荷载分布的比例相等[1]，因此，将作用在跨中的集中荷载近似转化为沿纵桥向的半波正弦分布荷载，沿横桥向分别施加在图4所示的13个位置上，依次计算，此时按各片主梁跨中挠度的比例来计算每片梁分配的荷载比例及荷载横向分布影响线。荷载作用在号梁时号梁的荷载横向分布影响线竖坐标值可表示为：

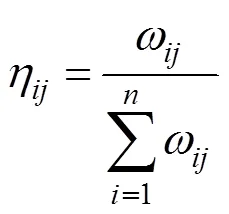
式中：ωij表示单位半波正弦荷载作用在j号位置时i号梁的跨中挠度；n为主梁数量。

3 有限元分析结果

3.1 榀内与榀间横向联结的数量对跨中荷载横向分布的影响

检验结果的拉曼光谱图如图1所示。通过分析谱图得出：10次测定结果的拉曼光谱图的特征峰数、峰位相同，峰形基本一致(忽略宇宙射线干扰)，表明实验仪器稳定性良好，利用该方法对塑料打包带(绳)进行检验，实验结果准确可靠。

横向联结系的具体布置为：榀内横撑数量按0道，3道，5道，9道考虑，榀间横撑数量按0道，2道，3道，5道，9道考虑，将榀内、榀间横撑数量进行不同的组合，共建立了10种布置情况的计算模型，后文图表中的数字-表示榀内道、榀间道横撑。

由于计算结果较多，仅给出1号，2号梁跨中截面的荷载横向分布影响线计算结果，见图5。从图中可以看出，在2种桥面板厚度下，跨中荷载横向分布随横向联结数量的变化规律相似：

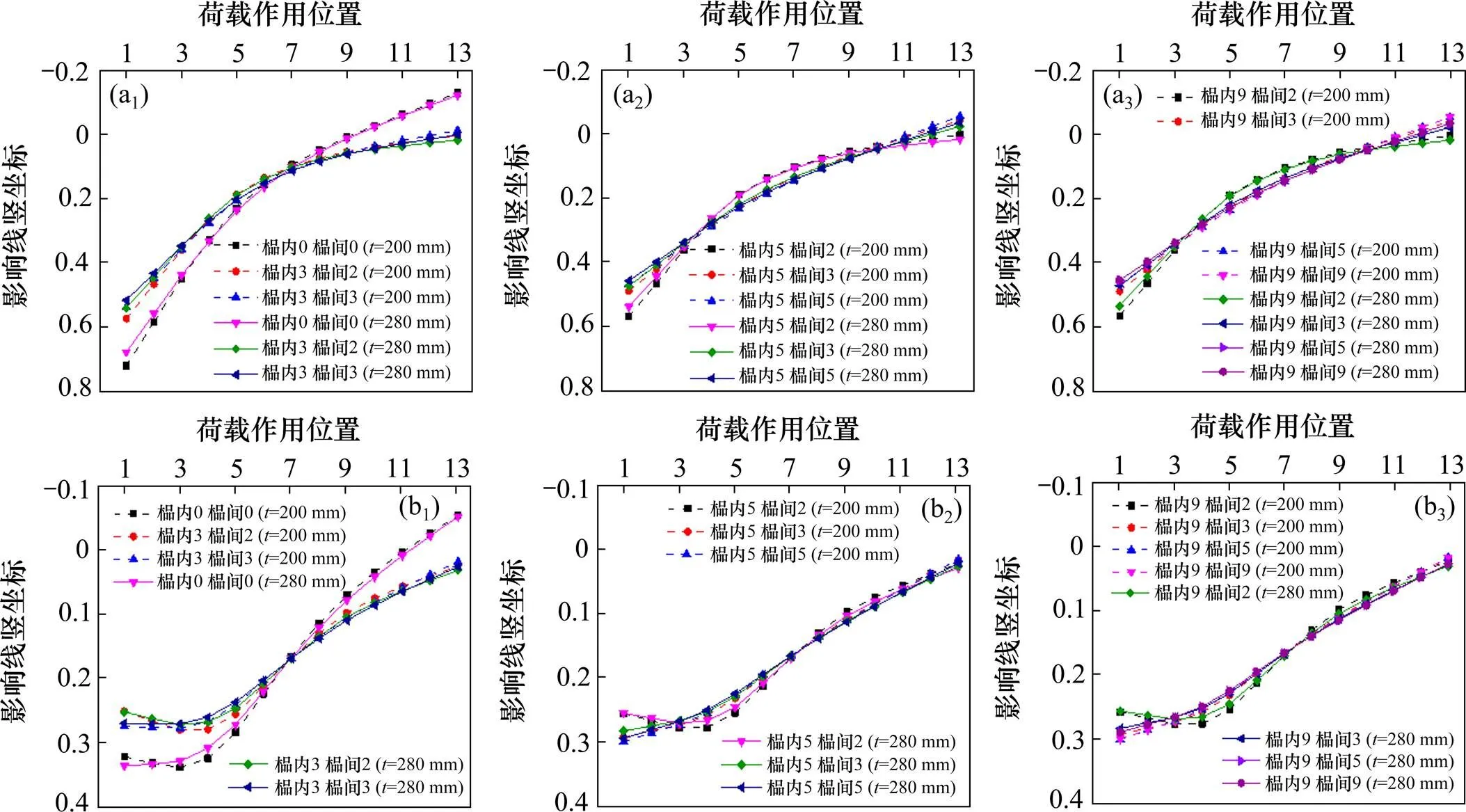
(a1)，(a2)，(a3) 1号梁；(b1)，(b2)，(b3) 2号梁

1) 无榀内、榀间横撑时，各主梁影响线的曲率较大，荷载作用梁位处的影响线竖标值较高，即直接承受荷载作用的主梁所分担的比例大，在2种不同的桥面板厚度下，1号梁分担的荷载比例最高分别达到72%，68%(即影响线竖标值×100%)；

2) 榀内有3道(端部和跨中横撑)、榀间有2道(端部横撑)时，各主梁影响线的竖坐标最大值相对无横撑时均有减小，1号梁分担的荷载比例最大值降至57%，54%左右；

3) 当榀内横撑增至5道，榀间增设1道跨中横撑时，各梁影响线的线型均发生了明显的变化。影响线的曲率大幅减小、从曲线趋近于直线，此时，1号梁分担的荷载比例最大分别下降至49%，47%，说明设置跨中横撑使荷载在跨中截面横桥向的分布更加均匀，主梁的整体受力性能得到增强；

4) 在榀内有5道、榀间有3道横撑的基础上，继续增加榀间横撑数量，影响线的曲率继续减小，但改变程度相对微弱，即榀间设置3～9道钢横撑对荷载横向分布的影响程度相近。

根据得到的各主梁影响线进行车辆最不利位置布载，按3车道布载求得荷载横向分布系数，计算结果示于表1。由表1可知：

1) 榀内、榀间均无横撑时，各梁的荷载横向分布系数相差较大；在2种桥面板厚度下，1号梁比2号梁的荷载横向分布系数分别高出约13%，15%；

2) 榀内有3道、榀间有2道横撑后，各梁的荷载横向分布系数均有所下降，1号梁的系数变化最为显著，下降幅度达22%，18%；同时，1号，2号梁系数的差值百分比下降，1号梁比2号梁分别高出约0.4%，7%；

3) 在榀内、榀间分别设置5道、3道横撑的基础上，继续增加横撑数目对荷载横向分布系数的影响较小；

4) 当榀内已经设置了9道横撑时，将榀间的横撑数由5道增至9道，影响线和横向分布系数几乎不再产生变化。

总的来看，在2种不同的桥面板厚度情况下，荷载横向分布影响线和系数随横向联结数量的变化规律是基本一致的：设置横撑能在一定程度上降低各主梁的跨中荷载横向分布系数；继续增加横撑数量，影响线的曲率减小，即主梁的整体受力性能增强，边梁的荷载横向分布系数则随之增加；当榀内横撑数量足够、榀间仅设置端部与跨中横撑时，继续增加榀内或是榀间横撑对于跨中荷载横向影响线及系数的影响程度很小。

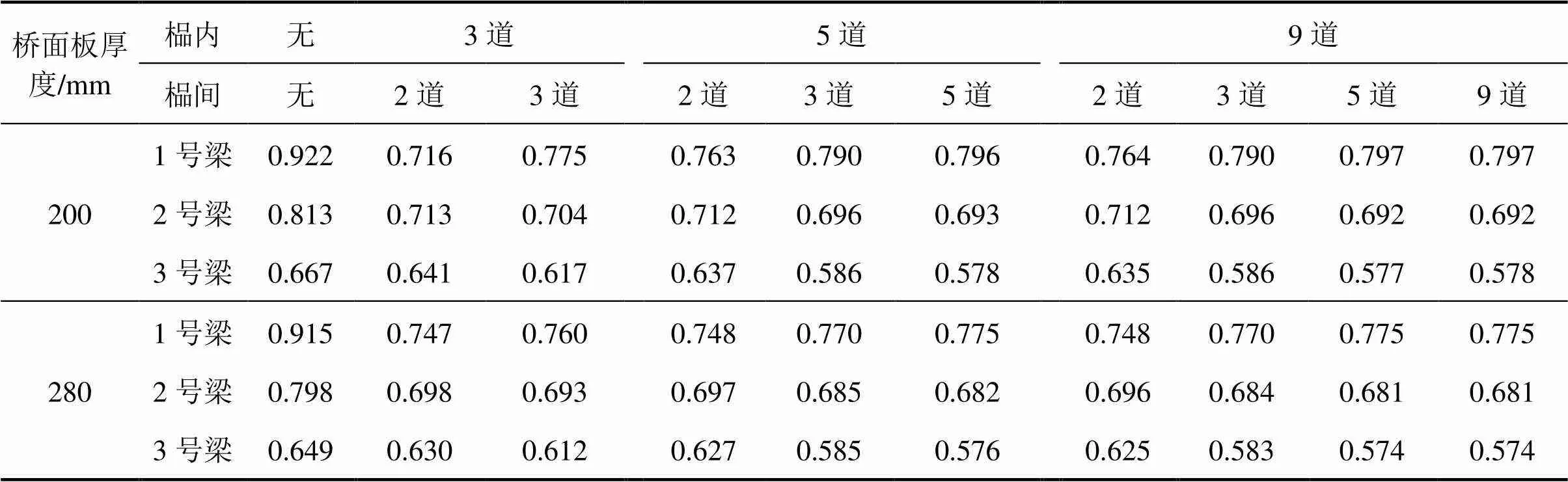
表1 各梁的跨中荷载横向分布系数

注：计算时不考虑横向折减系数。

3.2 横向联结的刚度对跨中荷载横向分布的影响

以榀内5道横撑、榀间3道横撑的情况为例，进一步研究横向联结刚度对荷载横向分布的影响。选取3种尺寸的钢横撑(∠125×12 mm，∠160×14 mm，∠200×14 mm)进行分析，荷载横向分布影响线及系数分别见图6和表2。

由计算结果可知：2种不同桥面板厚度下，跨中荷载横向分布随横撑刚度的变化规律基本一致：随着横撑尺寸的增大，各主梁的荷载横向分布影响线虽然有变平缓的趋势，但是变化幅度非常小。1号梁的荷载横向分布系数随着横撑刚度逐渐增大，而2号和3号梁的横向分布系数逐渐减小，系数的总体变化并不显著。可见，增大横撑尺寸对于荷载横向分布的影响有限。

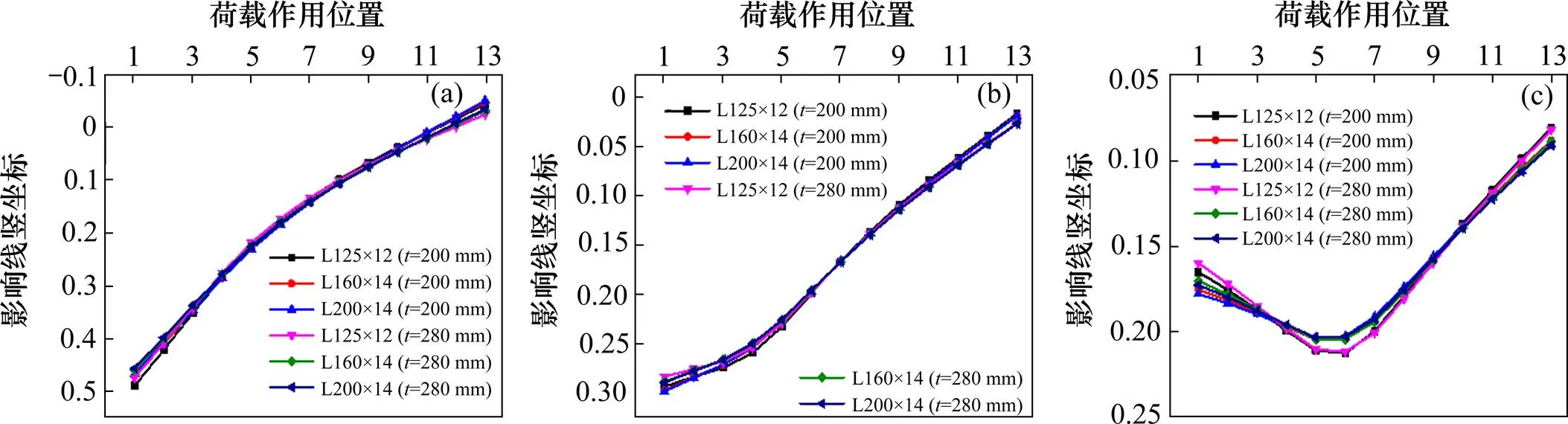
(a) 1号梁；(b) 2号梁；(c) 3号梁

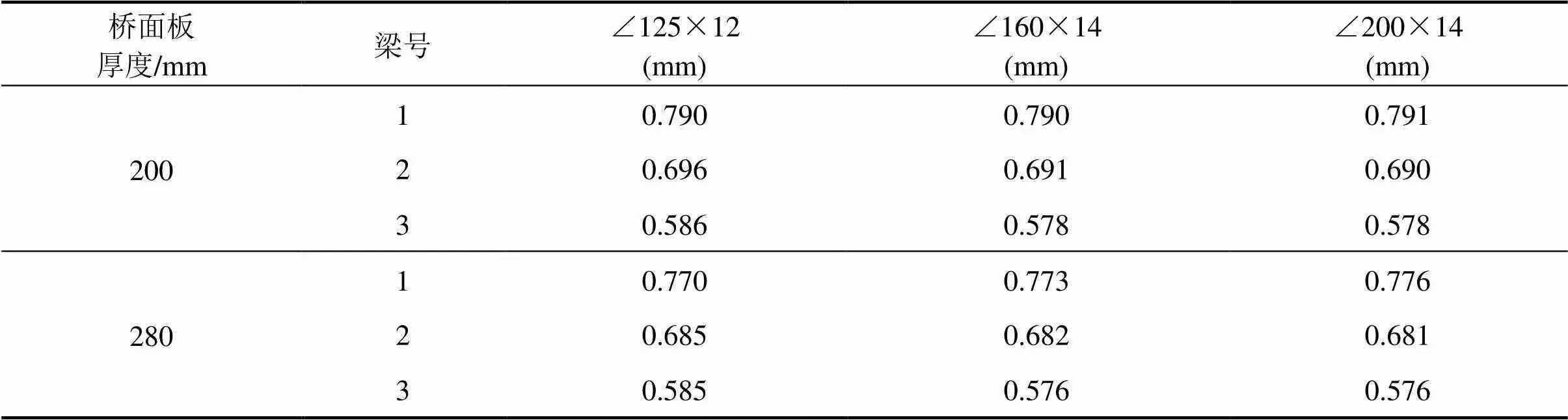
表2 不同尺寸横撑下的荷载横向分布系数

4 传统荷载横向分布计算方法的对比及适用性

4.1 跨中荷载横向分布系数

采用传统的刚性横梁法、刚接梁法计算跨中截面的荷载横向分布影响线及荷载横向分布系数，与有限元分析计算结果进行对比分析，得到1号和2号梁的结果列于图7和表3。

从图7可以看出：1) 对于全跨无横撑的情况，刚性横梁法与刚接梁法得到的影响线结果与有限元结果相近，但有限元法得到的影响线的曲率更大，即荷载向其他梁传递得少。这说明无横撑时，组合梁桥各主梁间的实际横向连接刚度小于刚性横梁法与刚接梁法假定的横向连接刚度；2) 对于榀内、榀间分别设置了5道、3道横撑的情况，1号梁和2号梁的有限元分析得到的影响线比刚性横梁法与刚接梁法计算得到的影响线斜率小，影响线竖标值在横桥向分布更均匀。

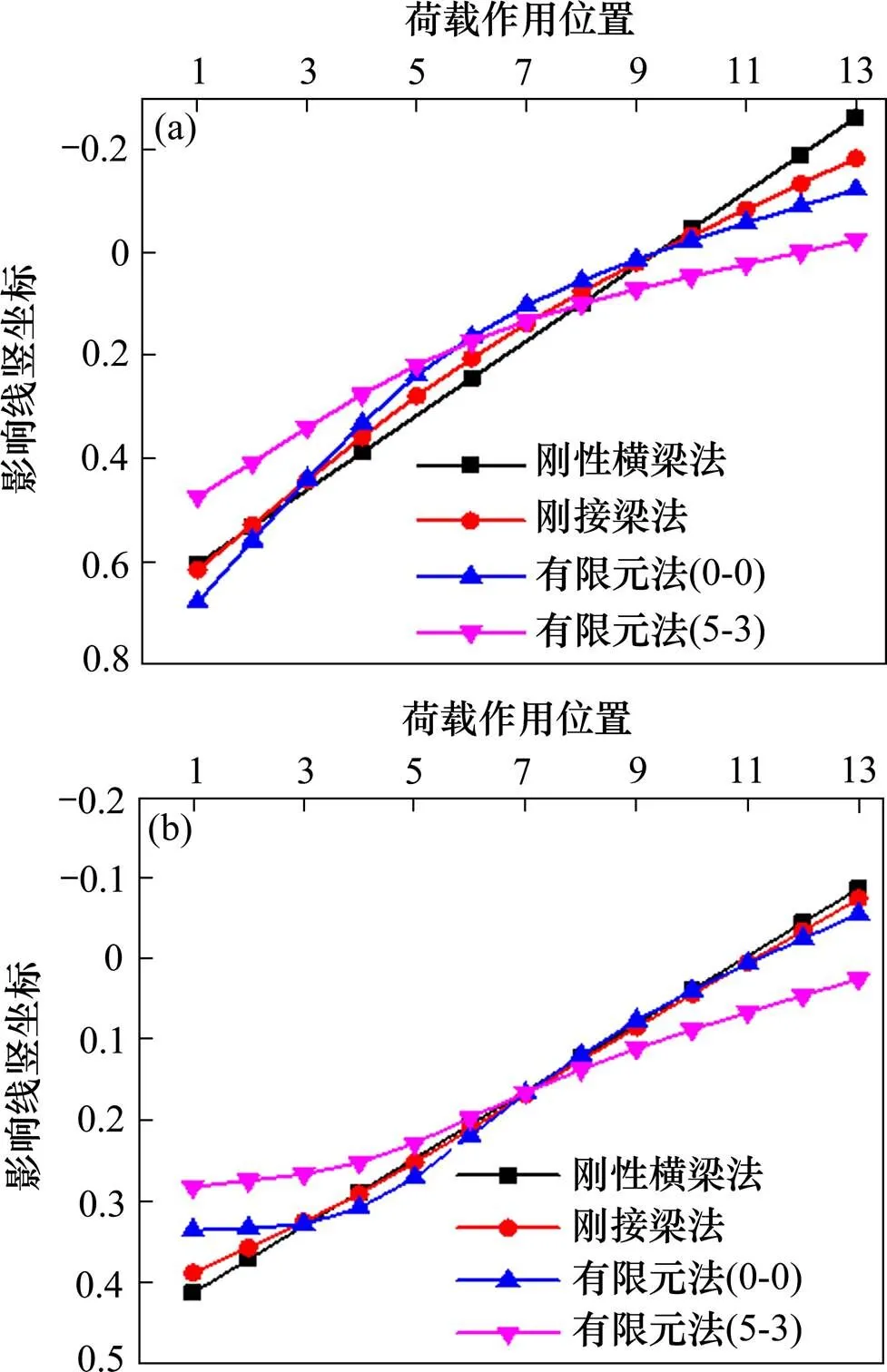
(a) 1号梁；(b) 2号梁

表3 传统方法与有限元法计算横向分布系数结果

注：0-0，5-3分别表示无横撑，榀内5道、榀间3道横撑的情况。

由表3可知：相对有限元结果，采用刚性横梁法、刚接梁法计算的1号梁荷载横向分布系数，在全桥无横撑的情况下偏高1.7%～7%，在设置钢横撑(榀间5道，榀内3道)的情况下偏高25%～36%，均偏于保守。因此，2种传统的跨中荷载横向分布计算方法对于设置了不等横向联结系的中等跨径窄幅钢-混组合桥仍具有适用性。

4.2 其他纵桥向位置的荷载横向分布系数

桥梁沿纵桥向各个截面的荷载横向分布系数可能均不相同，因此，本节针对沿纵桥的其他位置的荷载横向分布进行分析，研究传统理论方法在全跨荷载横向分布计算中的适用性。选取榀内5道、榀间3道横撑(桥面板厚度280 mm)的情况，在沿桥跨/100，/64，/32，/16，/8，/4，3/8的位置作用横桥向移动的荷载，得到各纵向位置1号、2号梁的荷载横向分布系数。

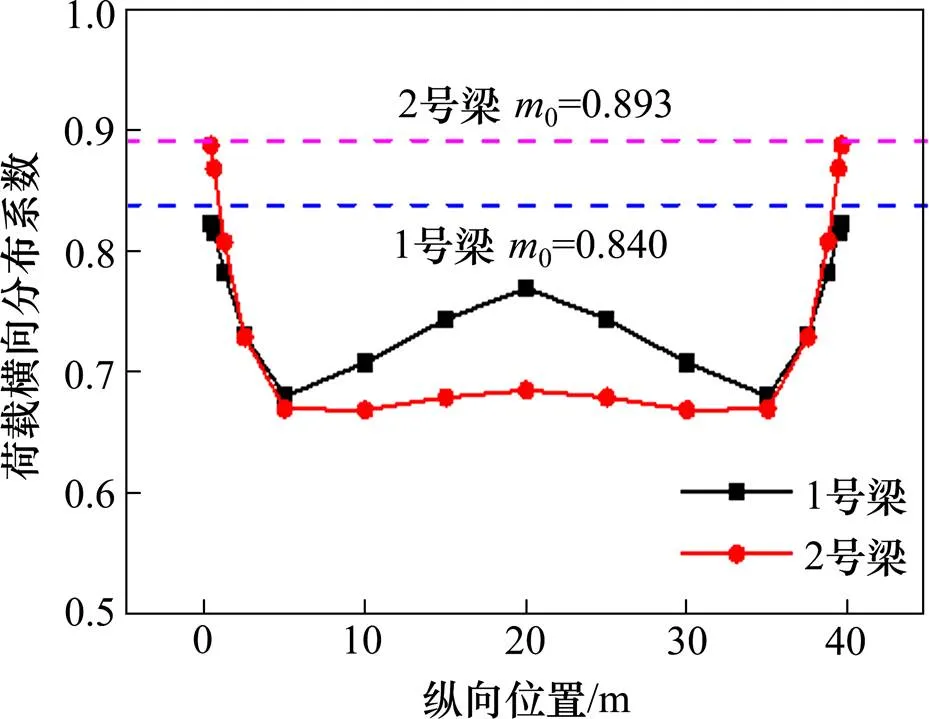
图8 荷载横向分布系数沿桥跨变化

图8实线部分为有限元分析得到的荷载横向分布系数沿纵桥向的变化，可以看出：支点附近到/8间，荷载横向分布系数下降得较快、近似于线性变化；/8到跨中位置，1号梁增长了约13%，2号梁几乎不变。图中虚线部分为采用杠杆原理法计算的支座处1号梁、2号梁荷载横向分布系数，大小分别为0.840、0.893，均大于有限元结果，偏于安全。

由4.1和4.2节的分析可知：实际设计时，支点处各梁的荷载横向分布系数可采用杠杆原理法进行计算，/8～/2区间采用刚接梁或刚性横梁法计算的跨中荷载横向分布系数，支点至/8区间内的荷载横向分布系数取线性变化。

5 结论

1) 榀内横向联结数量足够、榀间仅设置端部和跨中横向联结时，继续增加榀间横向联结横撑数量对荷载横向分布影响较小；设计时，榀间横向联结可仅在端部和跨中处设置，其余位置的横向联结则根据稳定性要求进行布置。

2) 横向联结刚度对荷载横向分布影响甚小。不同的桥面板厚度下，荷载横向分布随榀内、榀间横向联结的数量以及刚度的变化规律基本一致。

3) 采用传统刚性横梁法、刚接梁法计算得到的跨中截面荷载横向分布系数均大于有限元结果，偏于安全。

[1] 张凯. 中小跨径钢板组合梁桥快速建造技术与应用研究[D]. 西安: 长安大学, 2016. ZHANG Kai. Research on the accelerated construction technology and the application of composite steel plate girder bridge with medium-small span[D]. Xi’an: Chang’an University, 2016.

[2] Collings D. Steel-concrete composite bridges[M]. London: Thomas Telford Ltd., 2005.

[3] Helwig T, Yura J. Steel bridge design handbook: Bracing system design[M]. Washington D. C.: Federal Highway Administration ,2015.

[4] Jean-Paul L, Manfred A. 钢与钢-混组合桥梁概念和结构设计[M]. 北京: 人民交通出版社, 2014. Jean-Paul L, Manfred A. Steel bridges: Conceptual and structural design of steel and steel-concrete composite bridges[M]. Beijing: China Communications Press, 2014.

[5] 刘永健, 高诣民, 周绪红, 等. 中小跨径钢-混凝土组合梁桥技术经济性分析[J]. 中国公路学报, 2017, 30(3): 1-13. LIU Yongjian, GAO Yimin, ZHOU Xuhong, et al. Technical and economic analysis in steel-concrete composite girder bridges with small and medium span[J]. China Journal of Highway and Transport, 2017, 30(3): 1-13.

[6] American Association of State Highway and Transportation Officials, Bridge design specifications, 2004[S].

[7] 邵旭东. 桥梁工程[M]. 北京: 人民交通出版社, 2016. SHAO Xudong. Bridge engineering[M]. Beijing: China Communications Press, 2016.

[8] Abendroth R, Klaiber F, Shafer M. Diaphragm effectiveness in prestressed-concrete girder bridges[J]. Journal of Structural Engineering, 1995, 121(9): 1362- 1369.

[9] 张龙. 横梁对装配式钢筋混凝土简支T梁桥受力性能的影响[D]. 北京: 清华大学, 2015. ZHANG Long. Effects of the diaphragm on mechanical behavior of the simply supported fabricated reinforced concrete T-girder bridge[D]. Beijing: Tsinghua University, 2015.

[10] 闫君媛. 考虑车辆荷载横向位置随机性的中小跨径桥梁安全评估[D]. 长沙: 湖南大学, 2018. YAN Junyuan. Safety assessment of small and medium span bridges considering the randomness of transverse position of vehicle load[D]. Changsha: Hunan University, 2018.

[11] 冯宇. 钢-混组合梁加宽T梁桥的受力性能分析[D]. 西安: 长安大学, 2018. FENG Yu. Mechanical behaviour and analysis of steel- concrete composite widened T-girder bridges[D]. Xi’an: Chang’an University, 2018.

[12] Tabsh S W, Tabatabai M. Live load distribution in girder bridges subject to oversized trucks[J]. American Society of Civil Engineers, 2014.

Study on the effect of unequal transverse bracing systems on the transverse load distribution of steel-concrete composite bridges

LI Lifeng1, CHENG Zihan1, FENG Wei2, LIU Xinhua3

(1. College of Civil Engineering, Hunan University, Changsha 410082, China; 2. Xi’an Highway Institute of Shaanxi Province, Xi’an 710065, China;3. CCCC Second Highway Consultants Co., Ltd., Wuhan 430056, China)

At present, the construction technology that using double beams as a whole for hoisting is generally used in medium-span narrow steel-concrete composite beam bridges. The internal transverse braces are densely packed and prefabricated together with composite beams, while the external transverse braces are usually fewer to reduce site construction. To study the influence of this arrangement on the transverse load distribution and the applicability of conventional methods, a finite-element method was used to create several different models with a varying quantity and stiffness of internal and external transverse braces based on a 40 m steel-concrete composite bridge with different slab heights. Based on the FE analysis results, the applicability of the conventional rigid transverse beam method and rigid-jointed beam method were evaluated. These results are as follows. When the internal transverse braces are sufficient and external transverse braces are set up at the midspan and the ends, the increase of transverse braces has a small effect on the transverse load distribution; the stiffness of braces has limited effect on the transverse load distribution. The transverse load transverse distribution factors calculated through the conventional methods are greater than the FE analysis results, which is conservative.

bridge engineering; steel-concrete composite beam; transverse bracing system; transverse load distribution; finite element analysis

U448.216+6

A

1672 - 7029(2020)11 - 2832 - 08

10.19713/j.cnki.43-1423/u.T20191137

2020-12-16

国家自然科学基金资助项目(51978257)；陕西省交通厅科研课题(17-19K)；云南省交通厅科研课题(2017-17)

李立峰(1971-)，男，湖南沅江人，教授，博士，从事桥梁抗震、超高性能混凝土应用、钢桥与钢混组合桥基本理论等研究；E-mail：lilifeng@hnu.edu.cn

(编辑 蒋学东)