基于ITSRP模型的吕梁市水资源优化配置研究

单义明 杨侃 吴云

摘 要：针对区域缺水风险以及水资源配置中的不确定性与复杂性，在传统两阶段随机规划与区间线性规划的基础上，加入鲁棒性优化方法形成区间两阶段随机鲁棒规划（ITSRP）模型，不仅可以用离散的区间数表示水资源配置中的多重不确定性，而且可以实现模型的最优化目标与系统稳定性，提高模型的可靠性。将该模型应用于吕梁市的水资源优化配置中，当模型的鲁棒性因子达到一定值时，不同概率水平下的目标函数值均达到最优，最终得到吕梁市2025年水资源优化配置结果，表明模型具有较好的适用性。

关键词：水资源配置;不确定性;区间两阶段随机鲁棒规划;鲁棒性优化;吕梁市

中图分类号：TV213.9   文献标志码：A

doi：10.3969/j.issn.1000-1379.2020.11.009

Abstract： In view of the regional water shortage risk and the uncertainty and complexity in the allocation of water resources， on the basis of the traditional two-stage stochastic programming and interval linear programming， robust optimization methods were added to form an interval two-stage stochastic robust programming （ITSRP） model. The model could not only express the multiple uncertainties in the allocation of water resources with discrete interval numbers， but also realize the optimization goal and system stability of the model， and improve the reliability of the model. The model was applied to the optimal allocation of water resources in Lyuliang City. When the robustness factor of the model reached a certain value， the objective function values under different probability levels reached the optimal values， and finally the results of the optimal allocation of water resources in Lyuliang City in 2025 were obtained which showed that the model had good applicability.

Key words： water resources allocation; uncertainty; interval two-stage stochastic robust planning; robust optimization; Lyuliang City

水资源优化配置是一个复杂的不确定性问题，很多因子都难以精准预测。近些年来，很多专家学者都对不确定条件下的水资源配置方法进行了研究：Huang等[1]提出一种非精确两阶段随机规划方法，用于不确定性条件下的水资源管理系统，解决水资源分配问题;娄帅等[2]提出一种基于区间直觉模糊集的水资源配置群决策研究方法，提高了流域水资源配置方案的合理性;刘静[3]用多重不确定优化方法有效处理了水质和水资源系统的不确定性和复杂性。很多研究[4-8]采用区间两阶段随机规划方法（ITSP），但该方法在模型的可靠性方面有所欠缺，不能保证在不同概率水平下的目标函数值均达到最优。在水资源配置中，除了以经济效益最大化为目标外，还应该保证配置方案的可行性与可靠性。可行性指配置方案的实用性，实用性高则配置的缺水量小;可靠性指不同概率水平下目标函数值的平衡性，可靠性高則目标函数值的偏差小。区间两阶段随机鲁棒规划（ITSRP）模型将鲁棒优化方法与两阶段随机规划方法结合起来，是一种可以体现系统动态复杂性、保证系统可靠性的模型。本文以吕梁市为研究区域，将ITSRP模型应用于不确定条件下的吕梁市水资源优化配置中，综合分析用水效益与缺水风险，有针对性地提出不同情境下的用水对策，以期为吕梁市的水资源优化配置提供参考。

1 模型建立

在保证区域水资源承载力以及充分供水的前提下，以吕梁市的用水综合效益为第一阶段（将供水量作为第一阶段决策因素）、缺水引起的经济损失为第二阶段（将缺水量作为第二阶段决策因素），建立吕梁市两阶段随机规划模型。

1.1 目标函数

1.1.1 原始目标函数

2 实例研究

吕梁市位于山西省西部，经济社会的迅猛发展使得水资源供需矛盾日益突出，部分地区用水超出当地的水资源承载能力[9]。吕梁市多年平均降水量为498 mm，多年平均水资源总量约13亿m3，人均水资源量不足400 m3（仅为全国平均水平的14%）[10]，属于严重缺水地区，因此该地区水资源优化配置尤为重要。吕梁市辖1个市区、10个县，代管2个县级市，其区域供水网络概化见图2。

鉴于当地可供水总量的不确定性以及不同典型年不同概率下的可供水量不同，将可供水量离散为区间随机变量。根据2006—2016年《山西统计年鉴》和《山西省水资源公报》以及山西省吕梁市供水资料，预测2025年不同来水频率下的可供水量，见表1。

表2列出了吕梁市各行政区域各用水户2025年供水目标的上下限预测值，作为模型第一阶段的决策变量取值。其中：下限值参考《吕梁市水资源综合规划（2015—2030年）》中的数据，考虑到产业结构进一步优化调整，将其提高10%～20%作为不同用水户供水目标的上限值。

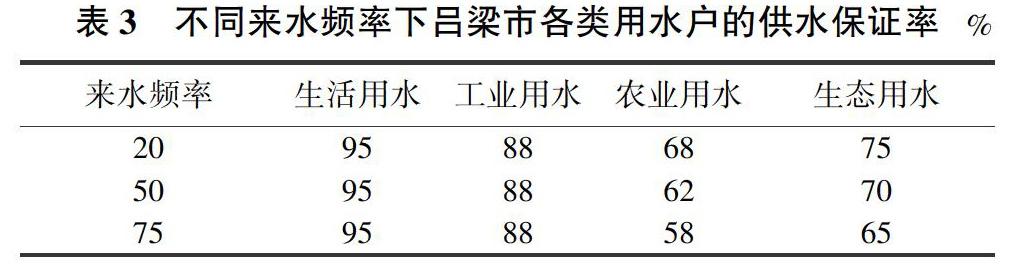
考虑到生态用水和农业用水在不同来水频率下的供水优先次序不同，表3列出了不同来水频率下的吕梁市各用水户的供水保证率。根据表3可求出各用水户的最小需水量，把其作为约束条件之一。

目标函数中的用水效益系数为用水收益减去用水成本所得的系数，参考文献[11-12]中的分摊系数計算方法及文献[13-14]中的山西省水价数据，得出用水效益系数;缺水惩罚参数主要由缺水时引外调水的成本以及缺水导致的经济损失决定[15]。由于成本相关系数存在不确定性，因此均采用区间数来表示，见表4。

3 结果与分析

3.1 水资源优化配置结果分析

根据表2可以得到不同来水频率下不能达到目标供水量的缺水水平，进而得到不同来水频率下吕梁市2025年水资源配置总量区间为[59 977.59，81 136.30]万m3。城市生活及生态用水应尽可能满足，取目标供水量的上限值W+ij（Zij，opt=1）;在以农业为主的地区应尽可能满足其农业需水要求（Zij，opt=1）;而以城市工业用水为主

（Zij，opt=0.71）以及一些农业占经济比重小的地区（Zij，opt=0）的目标供水应综合考虑区域发展过程中的用水综合效益，用水量较大的企业应控制生产规模，以确保区域水资源配置最优化。

表5列出了吕梁市2025年的水资源配置结果，缺水情况见表6。由表5和表6可以看出，不同来水频率下的配置均先按照预测目标供水量充分供水，不同用水户的配水量以及缺水量在较大程度上受来水频率的影响。丰水年时，区域内的生活用水、工业用水、农业用水、生态用水都可满足需求;平水年时，应首先满足生活和生态用水，但受来水量限制，工业、农业、生态用水均出现缺水情况;枯水年时，缺水情况最为严重，4类用水户均出现缺水，其中农业的缺水量最大。当来水较丰时，可充分分配可供水量，若分配不足则会出现惩罚成本的增加;当来水不足时，需要根据实际情况适当减少可供水量，维持系统的稳定性。

3.2 模型优化结果评价

采用ITSRP模型，考虑模型的不确定性，引入鲁棒优化方法，将水资源配置结果离散为区间形式。图3、图4为用水效益与鲁棒性因子的关系，可知：①鲁棒性因子越大，模型的上限和下限用水效益值越大，ρ≥5时用水效益基本不再变化，模型逐渐趋于稳定;②随鲁棒性因子的增大，用水效益的上下限差值逐渐减小至稳定值，模型的稳定性增强;③不同来水频率下的用水效益均在ρ增大到一定值时达到最优，体现了模型的平衡性和可靠性。对于用水户来说，如果供水量不满足需求，将直接影响其用水效益和产业发展;若供水量过多，则会导致供水成本增加或资源浪费。因此，应根据不同地区、不同用水户、不同产业综合分析，能满足供水目标时，大力发展用水效益高的产业，而在达不到供水目标时积极采取措施避免成本增加。

4 结 语

利用ITSRP模型，分析了吕梁市如何合理有效地分配水资源到各区域及各类用水户，以实现系统用水效益的最大化。配置结果显示，吕梁市2025年水资源配置总量区间为[59 977.59，81 136.30]万m3。丰水年时可按预测供水量给各类用水户充分供水;平水年以及枯水年时，城市生活以及生态用水应尽可能满足，在以农业为主的地区应尽可能满足农业需水要求，而城市工业用水以及农业占经济比重小的地区目标供水应根据其具体情况制定经济效益与缺水风险平衡的水资源配置方案。

在传统两阶段随机规划与区间线性规划的基础上，加入鲁棒性优化方法，构建区间两阶段随机鲁棒规划模型，以离散区间的形式表示水资源配置中的多重不确定性，提高了模型的可靠性，可保证在不同来水频率下的目标函数值均达到最优。

参考文献：

[1] HUANG G H，LOUCKS D P. An Inexact Two-Stage Stochastic Programming Model for Water Resources Management Under Uncertainty[J].Civil Engineering and Environmental Systems，2000，17：95-118.

[2] 娄帅，王慧敏，牛文娟，等.基于区间直觉模糊集的水资源配置群决策研究[J].长江流域资源与环境，2014，23（3）：319-327.

[3] 刘静.多重不确定性条件下流域水质管理与水资源配置[D].北京：华北电力大学，2017：134-135.

[4] 李晨洋，于伟铭，陈正锐，等.考虑生态的灌区水资源区间两阶段随机规划模型建立与应用[J].农业工程学报，2017，33（21）：105-114.

[5] 张成龙，郭萍，赵建明.不确定条件下的区间两阶段模糊可信性约束规划配水模型研究[J].中国农村水利水电，2016（8）：97-101.

[6] 曾雪婷. 随机模糊规划方法及流域水权交易研究[D].北京：华北电力大学，2015：152-157.

[7] XU Y，HUANG G H，QIN X S. Inexact Two-Stage Stochastic Robust Optimization Model for Water Water Resources Management Under Uncertainty[J]. Environmental Engineering Science，2009，26（12）：1765-1776.

[8] 刘敏.不确定性条件下的水库优化调度及水资源管理研究[D].北京：华北电力大学，2013：64-65.

[9] 米占萍.吕梁市水资源问题及对策[J].华北国土资源，2007，4（3）：32-34.

[10] 王春梅.吕梁市水资源现状及可持续利用对策[J].山西水利，2008，24（4）：32-33.

[11] 高波，郭菊娥，薛欣喜.沿海城市多水源多用户供水优化配置研究[J].中国海洋大学学报（社会科学版），2013，20（2）：19-24.

[12] 谷红梅，邱林，张民安，等.渭南市供水水资源优化配置研究[J].人民黄河，2005，27（12）：55-57.

[13] 许建武.山西省中型灌区水价探析[J].山西水利，2019，35（4）：20-22.

[14] 陈玮.山西省水完全成本测算及定价研究[D].北京：中国矿业大学，2011：67-79.

[15] 张静.不确定条件下城市多水源供水优化配置[D].北京：华北电力大学，2008：40-49.

【责任编辑 张华兴】