太阳帆板驱动装置高分辨率转速测量方法
2020-12-14郭超勇刘若莹于国庆
郭超勇,刘若莹,于国庆,张 猛,张 强
(1.北京控制工程研究所,北京100190;2.北京东方计量测试研究所,北京 100086)
为了应对高分辨率星载相机和高精度激光通信设备等有效载荷对卫星控制性能提出的挑战,卫星平台的指向精度和指向稳定度要求不断提高[1]。传统太阳帆板驱动装置(Solar Array Drive Assembly,SADA)一般都采用步进电机作为驱动源,造成太阳帆板在保持对日定向的连续转动过程中出现速率波动,并对太阳帆板的挠性模态产生激励,成为卫星Y 侧姿态控制性能的主要扰动源[2]。
提高整星姿态稳定度,降低乃至消除太阳帆板转速波动的不利影响是至关重要的手段之一[3],因此提出了SADA 采用永磁同步电机(Permanent Magnet Synchronous Motor,PMSM)直接驱动并实现转速闭环的高稳定度控制方案。PMSM 低速高性能驱动控制的关键技术之一是高精度、高分辨率位置和转速的检测和处理,从而实现更低的转速波动。旋转变压器由于其稳定、高效、抗冲击震动和温湿度变化小等优势,大量应用于航天器、机器人等工作环境恶劣的场合。航天器运动部件等要求在极低速场合下实现高稳定转速控制而不出现抖动、滑移、爬行等现象。因此,低速驱动速度高精度、高分辨率测量具有重要意义[4]。针对采用旋转变压器进行转速测量一般有以下两种方法:一种是直接通过对旋转变压器解码角度计算获得,另一种是构建速度观测器[5,6]。速度观测器基于整个伺服系统模型,与控制策略密切相关,其缺点是需要大量的先验知识,如整个系统的转动惯量、模态频率等,实际应用效果并不理想。文献[7]提出了一种针对旋转变压器-数字转换器(Resolver Digital Converters,RDC)输出的速度信号进行自整定滤波的方法,此方法针对极高的工作转速减少了速度误差,但对低速的效果未进行验证。Leonam Pecly 等[8]对转速测量采用位置直接差分、自适应数字滤波方法的优缺点进行比较,并提出了一种转速虚拟-模拟高通滤波方法;文献[9]针对旋转变压器的正余弦输出信号进行线性成形,通过改善信号质量来提高位置和速度精度;张梁等[10]针对速度观测所用Kalman 滤波器的噪声问题提出了采用粒子滤波器的方法。这些方法的缺点是计算相对复杂,且本质上并没有改善旋转变压器的低转速测量分辨率。
传统的测周期法(M 法)直接对旋转变压器角度周期差分得到转速易于实现,但在低速工况下存在分辨率不足、转速检测性能较差的现象。因此,迫切需要研究SADA 驱动系统的转速检测及控制方法。本文针对SADA 采用旋转变压器进行转速检测,根据检测的转速实现转速闭环控制,具有以下创新之处:
(1) 提出了一种基于旋转变压器的高分辨率频率法(T 法)测速及其FPGA 实现方案。在低速驱动场合,与传统周期法获取转速方法相比,具有更高的检测分辨率;
(2) 对提出的频率法测速进行实用化改进设计,与SADA 驱动特性及速度控制策略相结合,改善了低速驱动控制性能;
(3) 针对频率法测速产生的延时约束进行分析,结合SADA 驱动系统的转速控制策略,研究了驱动系统稳定的约束条件。
最后,仿真和试验结果表明了针对旋转变压器测角装置采用频率法测速可以显著改善SADA 驱动系统的测速分辨率及控制性能。
1 传统周期法转速测量
1.1 旋转变压器测角工作原理[11]
旋转变压器是一种测量旋转元件角位置和角速度的电磁式传感器,本质上相当于一种两相交流电动机。旋转变压器有几种类型,最常用的是正余弦旋转变压器,其结构示意图如图1所示。

图1 旋转变压器结构示意图Fig.1 Structure of resolver
正余弦旋转变压器绕组全部安置于定子中,而转子不安置绕组。其中,R1R2 为输入激磁绕组,S1S3为正弦输出绕组,S2S4 为余弦输出绕组。当激磁绕组R1R2 通入特定频率的正弦交流电压ur,正弦绕组S1S3 和余弦绕组S2S4 通过电磁感应分别输出与转角θ相关的正弦余弦值usin和ucos。

式中,n为旋转变压器的变比,Um和ωr为激磁电压幅值和角频率,θ为旋转角位置,t为时间。
针对式(1)输出的正余弦信号采用RDC进行解调,可以得到机构的绝对角位置。SADA 采用粗精双通道旋转变压器,其测角分辨率达到21 位,但仍难以满足低速工况下的测速分辨率要求。
1.2 在低速范围内角度差分测量转速方法的不足
根据旋转变压器及RDC 的特点,其转速测量采用测周期法进行角度差分非常容易实现。即在特定的采样周期内,测量旋转变压器的角度变化量来计算转速,测速原理如图2所示。

图2 周期法测速原理图Fig.2 Period-method for speed detection
周期法转速测量计算如式(2)所示:

式中,ω M为周期法计算得到的速度,M1为采样周期内旋转变压器输出的电机位置角度增量,k为采样周期序号,Tc为周期法转速测量的采样周期。
从式(2)可以看出,转速测量分辨率与角位置分辨率和采样周期相关。受限于重量、体积以及加工精度限制,进一步增加旋转变压器的解算分辨率非常困难。增大采样周期同样可以提高角速度测量分辨率,但是过大的采样周期导致延时增加从而影响SADA 的动态伺服性能。
在周期法测速方式下,旋转变压器角度变化量的分辨率为1 个当量,转速测量误差率计算如下:
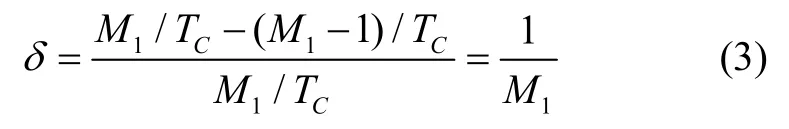
转速测量误差率与旋变测角变化量成反比,转速越低,M1越小,则误差率越大。因此,对于SADA极低转速工况,在一个采样周期内,周期法测速得到的M1变化缓慢且非常小,从而导致转速测量误差率δ极大,难以满足低速工况测量要求。
2 基于旋转变压器的频率法转速测量设计
2.1 频率法转速测量实现原理
光电编码器一般都具备输出A、B、Z 脉冲接口,采用频率法进行转速测量非常易于实现。然而SADA采用旋转变压器进行转速测量反馈,RDC 一般不具备此输出脉冲接口。因此,本文提出了一种基于旋转变压器的高分辨率频率转速测量及其FPGA 实现策略。通过FPGA 软件控制RDC 始终处于实时采集角位置模式,捕获数据总线的变化沿来实现频率法测速,其原理示意如图3所示。

图3 频率法测速原理图Fig.3 Frequency-Method for speed detection
图中,D[0…N]为RDC 输出的数据总线位,N为数据总线位次序,通过软件进行灵活配置;f0为高频采样时钟频率;M2为相邻两个跳变沿高频时钟计数,ΔT为相邻两个跳变沿间隔时间。
SADA 驱动系统实现的频率法转速测量计算结果如式(4)所示:

式中,θ N为频率法测速选择的第N位总线的角度分辨率。频率法转速测量的分辨率与高频时钟频率和角度分辨率有关。
采用频率法测速最多可能产生1 个高频计数时钟的误差,其转速测量误差率计算如下:
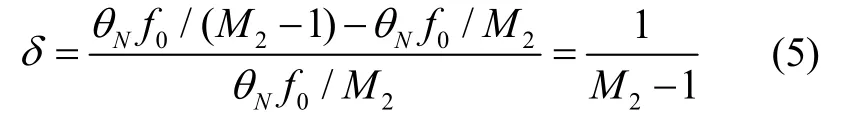
SADA 长期工作转速约为0.06 °/s,此工作转速下,数据总线相邻跳变沿间隔较长,高频时钟脉冲计数个数较多,误差率更小。因此,频率法测速非常适合SADA 低速运行工况。
2.2 FPGA 设计实现
针对旋转变压器测角装置的频率法测速实现简化框图如图4所示,FPGA 为频率法测速系统的核心,其时钟周期为40 MHz,通过控制RD 转换器始终处于测角转换和数据输出状态,并实时读取RD 转换器输出的数据总线沿变化以及方向信号。RD 转换器对旋转变压器在外部激磁产生的正余弦信号进行实时角度解算,通过数据总线对外输出角度数据。

图4 频率法测速简化框图Fig.4 Diagram of speed detection using frequency-method
为了实现旋转变压器的频率法测速,FPGA 软件内部设计了4 种状态:S0-S3,并根据触发条件实现状态转移,如图5所示。

图5 FPGA 状态机Fig.5 State machine of FPGA
接收到外部测速启动信号后,状态机进入S0 状态,完成高频时钟计数器清零,设置RD 转换器的实时工作模式等。当总线D[0…N]第K-1 个上升沿到来时刻,状态机进入S1 状态,此时计数器M2开始计数。当总线D[0…N]第K个上升沿到来时,状态机进入S2状态,计数器M2停止计数;然后进入S3 状态,完成计数器数据锁存及清零操作,并自动复位到S0 状态。
3 频率法延时约束与分析
3.1 频率法测速延时计算分析
旋转变压器采用频率法测速可以极大提高转速测量分辨率。通过式(4)和式(5)看出,转速测量分辨率与角位置检测分辨率和高频时钟频率有关。受硬件条件限制,时钟频率不能无限提高;角度分辨率取决于当前选择的第N位总线位,其中选择第0 位总线位角位置分辨率最高。当SADA 运行角速度一定时,数据总线跳变沿间隔ΔT随选择总线位N确定的角位置分辨率而变化,选取的总线位越高,间隔时间ΔT越长,高频计数M2也越大,相应的速度测量误差率也越小,但是,产生的转速测量延时会越长。为了提升SADA转速控制性能,需根据转速范围以及频率法测速导致的测量延时Td考虑选择相应的数据总线。

图6 频率法转速测量延时Fig.6 Speed-detection delay of frequency-method
图6描述了频率法转速测量产生的延时与SADA工作转速测量值和数据总线选取的关系曲线。由于SADA 驱动负载的低速特性,驱动控制性能要求的速度测量延时不可能无限降低,导致转速测量能够识别的最低转速将得到限制。
3.2 频率法限制及改进处理方法
通过式(4)获得SADA 低速工况下的转速并进行速度控制。当SADA 进行位置或速度保持控制时,转速接近零,此时FPGA 在非常长时间内检测不到旋转变压器角位置的变化沿,测量得到的间隔ΔT可能无界。这也将使得驱动系统的测量延时变得无限长,从而导致系统得不到真实稳定的转速。转速信号的输出也不能准确反映SADA 的工作状态。针对这种情形,在算法设计过程中,考虑设计频率法测量延时保护域值Tlim。在实际的位置跳变脉冲到来之前,采用如式(6)所示的方法进行转速测量的改进计算,ωT的正负由RDC 给出的方向信号进行确定。

根据式(6),当转速低于0.005 °/s 时,SADA 驱动系统长时间内得不到位置跳变沿,等效为驱动系统进入零速附近工况,结合RDC 方向信号,计算可得到SADA 的极低转速。其他情况根据测量得到的时间间隔ΔT进行转速计算。改进后的频率法获得的转速测量结果可以保证整个低速驱动范围频率法测量得到的转速信号都有界。因此,结合SADA 的速度控制策略可进行统一设计。
3.3 SADA 驱动系统稳定性分析
为了分析频率法测量延时带来的影响,对PMSM作为驱动源的SADA 驱动系统进行理论分析。首先,SADA 需要实现能量和信号传输,设计有功率导电环传输功率,信号导电环传输信号。导电环刷丝和盘环相对运动产生摩擦阻力,其负载模型为非线性,可采用Stribeck 摩擦模型描述:

式中,T c为库伦摩擦阻力矩,T m最大静摩擦阻力矩,ω s为Stribeck 角速度,σ为常数,经验选取范围1~2,B为粘性摩擦系数。
因此,SADA 低速驱动系统是一个高阶非线性的动态系统。为了分析方便,考虑电流内环响应远比转速环响应快,将电流环路等效为增益为1 的惯性延时环节,简化后转速环路控制框图如图7所示。

图7 伺服系统速度环结构图Fig.7 Speed-loop structure of servo system
对驱动系统的速度环路进行简化分析,将小时间常数环节合并为等效的惯性环节,则速度环控制对象传递函数为:

式中,JM为负载转动惯量,Ti为电流环等效时间常数,pn为PMSM 极对数,Φr为转子磁链,K ob为速度环等效增益,T∑n为速度环等效时间常数。
为了实现SADA 准确定向太阳,其转速控制要求无静差,因此速度环常采用经典PI 调节器,其传递函数为:

式中,k p为控制器比例系数,τ n为积分时间常数。
根据典型II 型系统设计,SADA 驱动系统控制参数设计为kp=7.3,τn= 0.03。为了分析所提出的频率法测速产生的延时对SADA 驱动性能的影响,在不同的频率法测速延时下进行系统频域对比,如图8所示。

图8 系统频域分析结果Fig.8 System frequency analysis results
随着转速测量延时的增大,系统的稳定裕量降低,性能变差;当转速测量延时时间接近或大于控制器积分时间常数时,系统的相位裕量接近0 度,系统稳定裕度不足将导致控制策略失效。因此,针对SADA 负载驱动系统,应结合高精度频率法测速带来的延时,需合理设计速度环控制参数。
4 仿真和试验验证
为了验证本文提出方法的正确性和可实现性,建立了相应的仿真和试验验证平台。针对SADA 转速测量分别采用传统周期法和改进后的频率法进行性能对比验证。仿真和试验平台所用的PMSM 和导电环负载参数如表1所示。

表1 验证平台负载参数Tab.1 Load parameters of verify platform
为了突出本文所提出高分辨率转速测量方法的优势,在SADA 巡航转速0.06 °/s 下,采用传统周期法测速以及本文提出的频率法测速进行了仿真对比,仿真结果如图9所示。通过两种方法得到的转速测量结果可以看出,在SADA 巡航转速0.06 °/s 下,旋转变压器测角装置采用周期法转速测量得到的转速波动范围为0.05 °/s-0.07 °/s,转速波动量约为0.02 °/s;采用频率法测速得到的转速波动范围为0.056 °/s-0.064 °/s,转速波动量约为0.008 °/s。与原有传统测速方法相比,转速波动量降低了约60%,且转速波动曲线更为平滑。

图9 SADA 低速仿真结果Fig.9 Simulation results of SADA at low speed
进一步搭建了SADA 驱动系统实物验证平台。为了验证所提出的针对旋转变压器频率法测速的有效性,对两种方法得到的转速分别进行反馈及高性能PMSM 驱动控制。转速评价采用同样的评价方法,为了排除传感器测量噪声的影响,对旋转变压器测量得到的角度进行100 ms 差分计算,从而得到SADA 的工作转速曲线。

图10 SADA 试验结果(0.06 °/s)Fig.10 Experiment results of SADA (0.06 °/s)
图10 描述了SADA 从零速切换至巡航转速的角速度波动情况。从试验结果看出,旋转变压器采用频率法转速测量具有更低的转速波动量,转速波动范围为0.055 °/s-0.065 °/s,转速波动量0.01 °/s;采用传统周期法进行转速测量,转速波动范围约为0.045 °/s~0.075 °/s,转速波动量0.03 °/s。两种方法对比,采用频率法实现转速测量反馈,驱动系统的转速波动量降低了约67%。
5 结 论
本文首先分析了SADA 旋转变压器测角装置采用传统测周期法测速分辨率有限的原因。在此基础上提出了针对旋转变压器实现低速驱动的高分辨频率法测量转速及其FPGA 实现方法。通过理论分析得到了频率法测速产生的时延对SADA 高性能驱动系统产生的影响,分析得出驱动系统的控制算法需与频率法产生的时延进行综合设计。最后,建立了SADA 驱动系统的仿真和试验验证平台。仿真结果表明,针对旋转变压器测角装置提出的高分辨率测速方法在SADA 工作转速下具有更低的转速波动,驱动系统的转速波动量降低了60%以上。进一步的试验验证结果也验证了本文所提方法的有效性。
