基于广义罗德里格参数的恒星相机和陀螺联合测姿方法

尹 潇，柴洪洲，杜祯强，向民志，石明琛

（信息工程大学地理空间信息学院，郑州 450001）

航天器控制的重要前提是确定航天器的轨道和姿态，而其中姿态信息对于航天任务的完成至关重要。因此，相关学者对姿态测定的传感器及算法进行了深入研究[1-2]。特别地，随着我国测绘卫星将配备恒星相机，利用恒星相机和陀螺联合测姿成为一种相对应用广泛的方法[3]。该方法兼顾恒星相机的高精度姿态四元数信息和陀螺的高频角速度信息，可实现高精度高频率的姿态获取。

在进行恒星相机和陀螺数据融合时，多采用四元数进行状态传递，然后采用三个姿态角误差进行测量更新[4]。当姿态扰动误差较小时，利用姿态角误差进行测量更新，并对更新获得的四元数进行强制归一的方法适用性较好[5]。但当状态初值不准确时，四元数强制归一会引起估计的误差。

因此，文献[6]提出一种基于广义罗德里格参数的误差四元数更新方法，其通过四元数的乘法特性，保持了更新后的四元数的归一化性质。另外，与经典Gibbs 向量和改进的罗德里格参数(Modified Rodrigues Parameters,MRPs)相比，广义罗德里格参数不存在180 °和360 °的奇异现象[7]。考虑文献[6]采用三轴磁强计且没有给出具体的算例，有必要进一步分析，不同初始姿态精度时，广义罗德里格参数对于恒星相机测姿的影响。

另外，在进行姿态估计时，常采用扩展卡尔曼滤波(Extended Kalman Filter,EKF)，其算法简单且易于实现，但该算法忽略了高阶信息，较适合于弱非线性的系统。对于强非线性和非高斯环境，常采用采样趋近的方法逼近后验概率密度分布，经典的算法有文献[8]提出的无迹卡尔曼滤波(Unscented Kalman Filter,UKF) 和文献[9]提出的粒子滤波(Particle Filter,PF)。但PF 计算量较大，且容易出现粒子退化，较难满足导航实时性的需求[10-11]。为此，在状态初值不准确时，有必要研究采用UKF 进行姿态估计[12]。特别地，对于恒星相机的非线性测量方程，利用UKF 进行测量更新优势较为明显。另外，相较文献[12]，有必要分析不同缩放参数对于恒星相机和陀螺联合测姿的影响，确定基于广义罗德里格参数采样的策略。

为此，本文首先给出广义罗德里格参数的构造方法以及其与四元数的关系，并详细介绍其在四元数归一化中的应用。然后，介绍基于陀螺角速度的运动学方程以及基于恒星相机的测量方程，并给出UKF 的详细流程。最后将本文算法应用于旋转航天器的姿态估计，并与EKF 结果比较，验证算法的有效性。

1 广义罗德里格参数

在描述航天器姿态时，常采用的方式包括欧拉角、方向余弦和四元数。其中，欧拉角在接近90 °时，会出现退化现象，仅适合于姿态变化不大的情况[13]。方向余弦避免了退化现象，但方向余弦包含九个未知量，计算量大，难以满足实时性的要求。因此，多选用四元数表达姿态信息[14]：

由于利用四个数表达三维姿态，四元数满足以下的约束条件：

式(2)也称为归一化条件。利用四元数表达姿态矩阵，表达为：

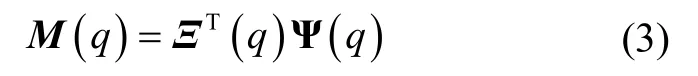
其中，

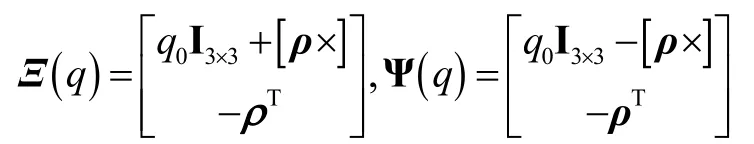
I 为单位阵，［ρ×］为向量ρ的反对称矩阵，即：

由四元数表示的姿态运动学方程为：

式中，ω为经过陀螺零漂改正的测量角速度向量。在高采样的情况下，可近似认为ω在相邻时刻的方向固定不变，则姿态运动学方程可离散为：

其中，

式中，为修正后的四元数，δα为测量更新估计得到的三个姿态角扰动误差。式(6)修正后的四元数在大的初始状态偏差时仍然需要进行强制归一化，即：

为此，本文采用广义罗德里格参数建立误差运动学方程，其表达式为[6]：

式中，δ p为罗德里格参数，其为三维向量；f为比例因子；a为常数，通常取0 ～ 1。当a= 0,f= 1时，式(8)为Gibbs 向量，其存在180 °的奇异；当a= 1,f=1时，式(8)为MRPs，其存在360 °的奇异。因此，本文取a= 1,f= 2 （a+ 1）计算式(8)，其不存在奇异，称为广义罗德里格参数，其与误差四元数的关系为：

当由测量更新计算出δ p的估值后，即可以采用(9)式计算出误差四元数，再利用四元数乘法修正式(5)，即：

式中，⊗表示四元数乘法。由于连续旋转不会改变向量的模，因此四元数乘法保持了四元数归一化特性。因此，采用广义罗德里格参数建立运动学方程，然后转换为误差四元数进行乘法修正可有效避免强制归一化引起的误差。

2 基于恒星相机和陀螺的UKF 姿态确定

2.1 姿态运动学方程

式(5)给出离散的姿态运动学方程，其由陀螺测量的角速度进行更新。陀螺的测量模型一般表示为[15]：

式中，为陀螺测量的角速度；β为陀螺零漂，为待求参数；nv和nu分别为测量白噪声和随机游走噪声，二者满足均值为零的高斯分布，且二者独立，方差分别为σv2和σu2。

2.2 恒星相机测量方程

利用固定在航天器上的相机拍摄恒星照片，获取恒星像点坐标bi与其惯性系坐标的共线方程，即可求解航天器的姿态。因此，可以建立如下的测量方程：

其中，

式中，i为观测恒星的编号；（xi,yi）为像点坐标；f0为相机焦距；ri为恒星在惯性系的坐标，为已知值；M为待求解的姿态矩阵；Vi为观测噪声，近似服从高斯分布，即：

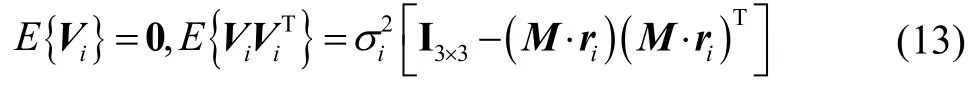
式中，σi2为测量噪声的方差。

2.3 UKF 姿态估计

根据2.1 可知，姿态估计中的参数包括四元数和陀螺零漂，共计七个参数，即：

但在测量更新时，采用广义罗德里格参数，即：

其中，δ p为零向量。下面给出UKF 采样变换的方法，其主要通过构造一组Sigma 点集(2n+ 1)，以及相应的权系数Wim和Wic来近似逼近状态分布的均值和方差[8]。权系数常用式(16)表达：

式中，n为状态参数的个数；λ为缩放参数，一般取λ= 3-n。具体算法实现的流程总结于表1。

表1 UKF 姿态估计算法Tab.1 UKF for attitude estimation

其中，过程噪声按照文献[6]的方法确定，计算公式如下：

3 仿真试验及分析

将提出的基于广义罗德里格参数改进的UKF 姿态估计算法应用于恒星相机和陀螺的联合测姿试验，并与EKF 算法的结果对比。试验中航天器的轨道周期约90 min，恒星相机的采样频率和陀螺的采样频率相同，本次试验取1 Hz。陀螺的常值零漂噪声σv、随机游走σu，初始姿态q0、零漂β0及其方差P0，以及恒星相机的测量噪声σs如表2所示。

表2 参数设置Tab.2 Configuration for technical parameters

首先按照表2给出的姿态和零漂初值进行EKF 及UKF 姿态估计，此时初始状态精度较好，结果如图1所示。

图1(a) EKF 估计的姿态角误差Fig.1 (a) Attitude errors of EKF

EKF 估计姿态时，采用式(6)强制归一化的方法；UKF 估计姿态时，采用广义罗德里格参数构造误差四元数的方法。由图1可看出，横滚角、俯仰角的精度明显优于偏航角，这与航天器的飞行状态是相符的。另外，三倍中误差边界很好限定了姿态误差，也表明姿态估计精度较优。对比EKF 和UKF 的估计结果，可看出二者没有明显的差异，表明在初始状态准确时，UKF 并没有优势，采用强制归一化引起的误差也可以忽略。

下面给初始姿态角分别加50 °、50 °和160 °的误差，仅采用EKF 估计，但分别采用式(6)和式(10)进行四元数更新，三维姿态误差的比较见图2。由图2可以看出，采用广义罗德里格参数构造误差四元数的方法精度优于强制归一化的方法。统计两种方法的平均RMS 分别为6.79 °和6.17 °，进一步表明在初始姿态偏差较大时，采用广义罗德里格参数构造误差四元数的方法可有效改善强制归一化引起的误差。

采用同样的初始姿态角偏差，分别采用EKF 和UKF 进行姿态估计，并皆采用式(10)进行四元数更新，重新进行一次试验，见图3。由图3可以看出，在初始姿态存在较大偏差时，UKF 精度明显优于EKF。

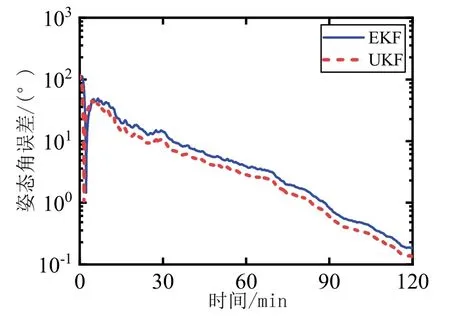
图3 EKF 和UKF 的姿态角误差比较(初始姿态偏差)Fig.3 Attitude errors comparison between EKF and UKF(Initial attitude errors)

在同样的初始姿态角偏差基础上，另外在偏航方向加10 °的初始零漂误差，分别采用EKF 和UKF 进行姿态估计，并皆采用式(10)进行四元数更新，再次进行一次试验，见图4。由图4可以看出，在初始姿态和零偏同时存在较大偏差时，EKF发生明显的震荡，无法收敛。相比EKF，UKF 仍然可以收敛至0.1 °，再次表明UKF 性能优于EKF。

图4 EKF和UKF的姿态角误差比较(初始姿态和零漂误差)Fig.4 Attitude errors comparison between EKF and UKF(Initial attitude and bias errors)

上述试验时，取缩放参数λ=- 3。但由于缩放参数影响UKF 的采样分布[6]，本文进一步研究λ取值不同对恒星相机和陀螺联合测姿的影响。采用如上的初始姿态和零漂误差，试验结果如5 所示。由图5可以看出，λ=-3 时姿态角误差最大，表明进行非线性变换后，状态参数分布不再是高斯分布。更进一步采用同样的50 次蒙特卡洛试验，统计每次结果的RMS，如图6所示。由图6可以看出，λ= -3 时精度最差；λ=-2 和λ=-1 时，波动也较大；λ= 0时，大部分精度最优，但出现一次明显的误差；λ= 1时，稳定性和精度总体最优，这与参考文献[6]的结论一致，再次表明在进行非线性的无迹变换后，状态参数分布不再是高斯分布。

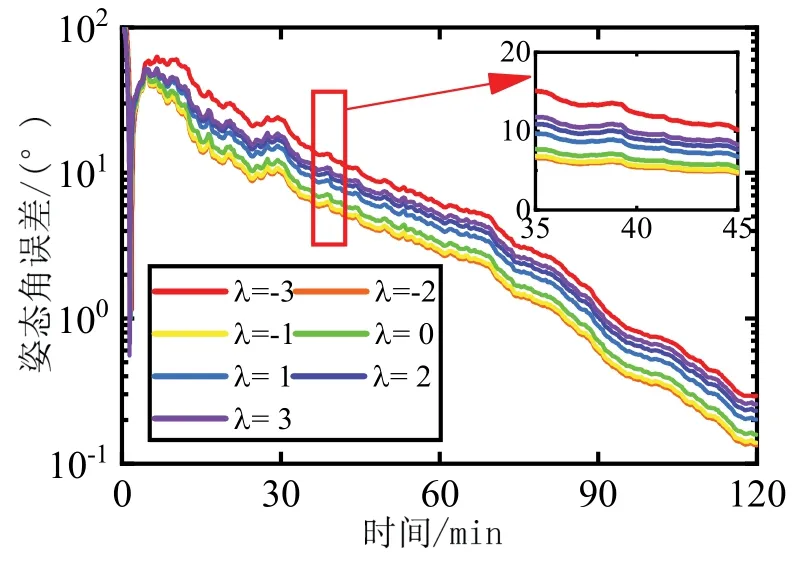
图5 采用不同缩放参数的姿态角误差Fig.5 Attitude errors using different scaling parameters

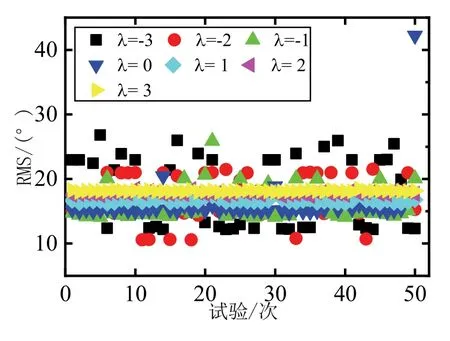
图6 采用不同缩放参数的姿态角RMS 统计Fig.6 RMS of attitude errors using different scaling parameters

4 结 论

本文首先推导了基于广义罗德里格参数构造误差四元数进行乘法更新的方法，并通过试验分析该方法对强制归一引起误差的改善。在此基础上，本文给出基于UKF 的恒星相机和陀螺测姿算法流程，并与EKF比较。仿真试验表明，在状态初值不准确时，UKF 在收敛速度和精度上都优于EKF。并且，经过非线性无迹变换后，状态参数的分布不再是高斯分布，缩放参数在λ= 1时估计最优。另外，UKF 计算非线性观测方程时所需运算量大于EKF，下一步需要优化算法处理速度。