基于IMU预积分封闭解的单目视觉惯性里程计算法

徐晓苏，吴 贤

（1.微惯性仪表与先进导航技术教育部重点实验室,南京 210096；2.东南大学仪器科学与工程学院,南京 210096）

使用低成本的传感器在移动设备和机器人上实现高精度的3D 导航，在增强现实和自动驾驶等实际应用中具有巨大意义。为此，利用惯性导航定位方案实现室内三维场景定位，该方案利用惯性测量单元(IMU)测量传感器平台三轴角速度和线性加速度，并将其刚性附着在传感器平台上。通常，IMU 工作频率很高(如100～1000 Hz)，使它能够测量高速运动。然而，由于传感器噪声和偏置的影响，单纯使用IMU 测量很容易导致失败的运动估计。因此，研究人员开发了视觉惯性组合导航定位系统（VINS）[1]，该系统融合至少一个摄像机的辅助信息来限制累积的惯性导航漂移，从而实现高精度的运动估计。再过去的十几年中，视觉惯性导航系统取得了巨大的进步，研究人员开发出了许多应对不同环境和功能的视觉惯性融合算法[2-4]。

融合相机和IMU 数据进行运动估计的算法统称为视觉惯性里程计（VIO），根据其实现途径，可以分为基于滤波器的VIO[5]和基于优化的VIO[6]。传统上，基于滤波的算法主要是通过扩展卡尔曼滤波器(EKF)来实现，其中IMU 测量载体的运动数据和相机测量的地图特征点分别被用来运动传播和更新状态估计。然而这些滤波器方法不更新被边缘化的历史状态，从而导致它们容易出现漂移。文献[7]提出了一种基于双目多状态约束下的卡尔曼滤波器（MSCKF）并结合Lucas-Kanade（LK）光流法的视觉惯性里程计算法，该算法能够在相机抖动和纹理缺失等情况下的精准位姿估计。相比之下，基于优化的算法同时处理在一个轨迹上的所有测量，估计平滑的载体状态，这些方法由于能够实现非线性测量方程并修正历史的状态估计，从而能够获得较高的运动估计精度。然而基于优化的方法需要处理所有的IMU 高频数据，具有较大的计算复杂度；相比之下基于扩展卡尔曼滤波的方式能够有效地处理IMU 数据并更新，速度快并且能够实时运行。

基于滤波的视觉惯性里程计算法主要是基于紧耦合的方式，即使用相机和IMU 传感器的数据共同进行运动估计[8]。该类型算法中的EKF-SLAM[9]将IMU 状态和相机观测到的地图点共同放入系统状态量，从而实现运动估计，但是由于状态向量维度非常大，使得运算效率很低并且精度不高。研究人员对EKF-SLAM算法进行了一系列的改进，包括ACK-MSCKF[10]、MSCKF[1]、Trifo-VIO[11]等算法。MSCKF 算法同样以EKF 滤波器为框架，采用一个滑动窗口来维护多个时刻的相机位姿，而不是三维地图点，从而有效解决了EKF-SLAM 系统状态向量维度过大的缺点，并且能实现较高的精度和实时性，但是MSCKF 对IMU 数据处理采用龙格库塔数值积分法，通过多次迭代计算出两帧图像间的IMU 速度和位置量，这种算法导致较大的计算量，加重了CPU 的计算负担，同时MSCKF 算法观测方程中的特征点逆深度化方法存在当z 轴方向趋近于零时会出现奇点的情况，使得这种算法存在一定的缺陷。文献[12]实现了双目版本的MSCKF 算法，并且将IMU 和相机之间的标定外参数加入到系统状态量中，实现在线标定，有效增加了系统的可观测性和一致性，并且实现了小型飞行器的定位功能。文献[13]对MSCKF 进行改进，将主参考系设置成机器人本体坐标系，而不是以世界坐标系为参考系，并且对IMU数据处理采用IMU 预积分算法，有效增加了系统的计算效率和定位精度。文献[14]提出了一种基于优化框架下的VIO 算法，同时采用IMU 预积分方法处理IMU数据，然而这种IMU 预计分算法通过离散的解来简化所需的预积分数值，而不计算出积分方程的闭式解。

上述MSCKF 框架下算法在处理相邻图像帧之间的IMU 数据时通常使用数值积分，从而递推得到下一个图像帧到来时的IMU 状态量初始值估计，这种数值积分的方法增加了系统的运算量，针对此问题，本文对MSCKF 中IMU 处理算法进行改进，提出了一种基于闭式解的IMU 预积分方法来替代数值积分。同时针对MSCKF 算法观测方程中的特征点逆深度化方法存在当z 轴方向趋近于零时会出现奇点的情况，本文提出了一种新的逆深度参数化方法，该方法提升了系统的鲁棒性和数值稳定性。通过EuRoc 数据集实验表明，本文的改进方法能提高MSCKF 框架下基于扩展卡尔曼滤波器的视觉惯性里程计算法精度。

1 基于封闭解的IMU 预积分算法

IMU预积分技术被广泛地用于视觉惯性融合算法中，传统的基于优化框架的VIO 算法通常在分段常数加速近似下采用离散解来简化所需的预积分，使得VIO 系统定位结果不高，为了提升VIO 系统的定位精度，本文提出一种基于封闭解的IMU 预积分方法，并应用于MSCKF 框架下基于扩展卡尔曼滤波器的VIO系统。

IMU 通常测量载体的角速度w和加速度a，其测量值表示为:

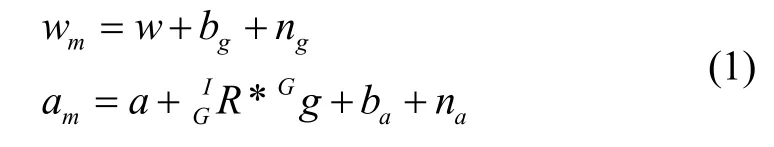
式中，wm和am分别表示IMU 陀螺仪和加速度计的测量值；w和a分别表示陀螺仪和加速度计的真实值；表示世界坐标系G到IMU 系I的旋转矩阵；b g和ba分别为陀螺仪和加速度计的随机游走偏置；n g和na分别表示陀螺仪和加速度计的零均值高斯白噪声。Gg表示重力加速度矢量。

类似于MSCKF 算法，k时刻系统IMU 状态向量定义为XI：

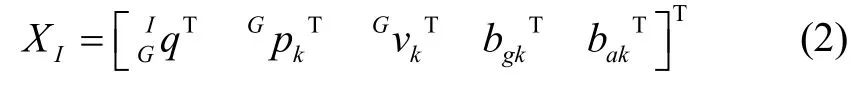
式中，GIq表示世界坐标系G到IMU 系I的单位旋转四元数；Gpk和Gvk表示k时刻IMU 在世界坐标系G中的位置和速度。

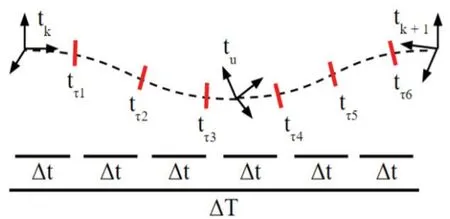
图1 在图像帧时刻到之间进行IMU 采样，采样间隔为ΔtFig.1 IMU sampling between image frame time tkandtk+ 1,sampling interval is Δt

由文献[15]，第k+1刻的IMU 位置、速度和旋转矩阵可以由第k时刻递推得到，方程如下：

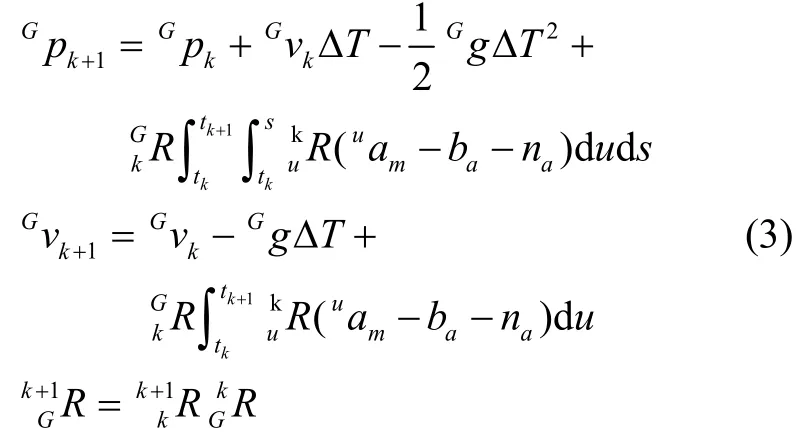
式中，ΔT=tk+1-tk，表示相邻图像帧时间间隔，如图1所示；式(3)预积分项记为kαk+1，kβk+1，且：

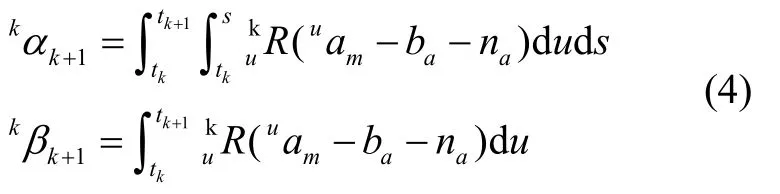
连续时间旋转四元数方程为：

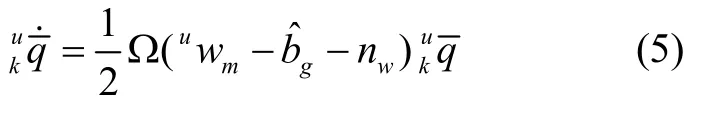
对式(5)进行零阶四元数积分求解出不同时刻的旋转四元数[16]。基于式(4)的定义，预积分项动态方程如下：

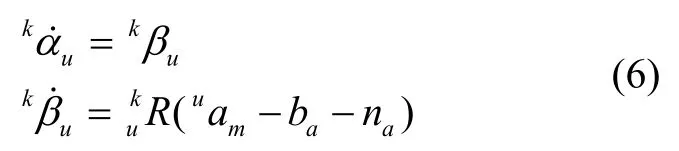
由式(6)动态方程，得到预积分估计值的线性系统方程如下，

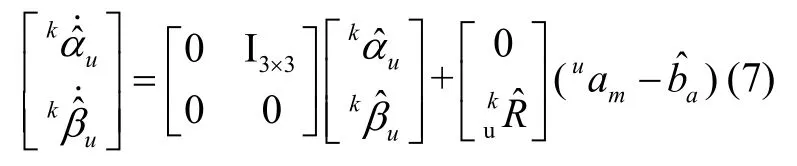
对式(7)积分，得到预积分项闭式解：

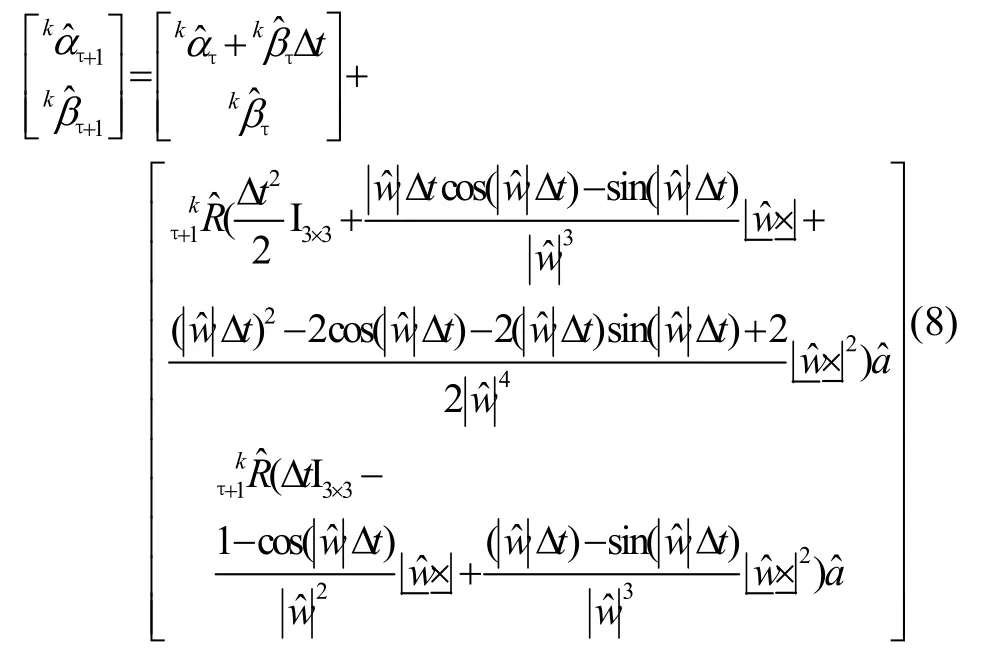
式中，Δt表示IMU采样间隔，Δt=tτ+1-tτ，表示加速度估计值，且。根据式(5)(8)得到相邻图像帧时刻的IMU 预积分项，再代入式(3)中得k+1时刻的位置、速度和旋转值。

2 基于封闭解预积分的IMU 模型传播

本文提出的基于扩展卡尔曼滤波器的视觉惯性里程计融合定位方法，其系统状态向量包括两个部分，分别为IMU 状态向量和基于滑动窗口的N 个历史相机位姿，系统状态向量为：

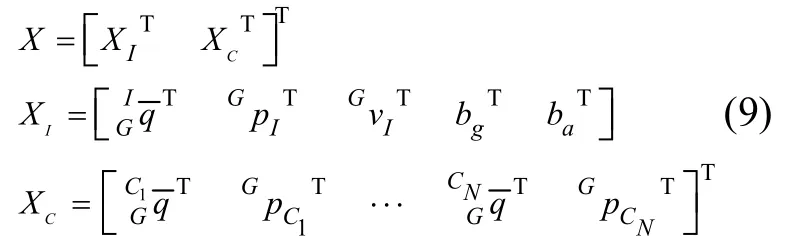
式中，XI表示k时刻IMU 的系统状态；XC表示N个历史相机位姿。

2.1 连续时间IMU 状态误差模型

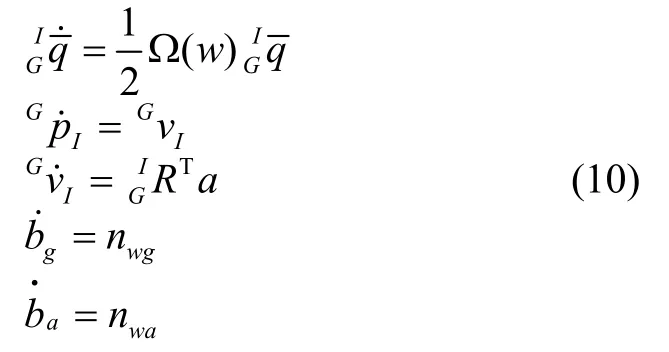
类似于MSCKF 算法，连续时间系统中，IMU 运动模型为：根据式(1)(9)(10)，IMU 观测向量的传递模型可以表示为：

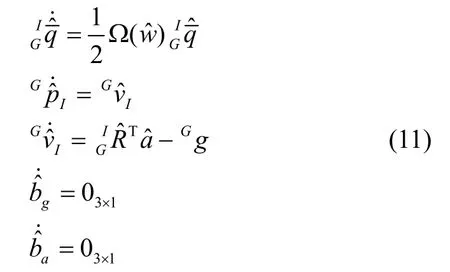
定义四元数误差向量为，则：

式中，表示旋转误差项；表示位置误差项；表示速度误差项；和分别表示陀螺仪偏置误差项和加速度偏置误差项。此时，系统误差表达式可以定义为：

式中，表示相机状态误差，可以定义为：

根据式(10)～(15)，连续时间IMU状态误差方程为：

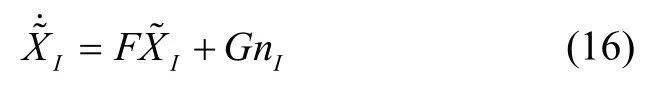
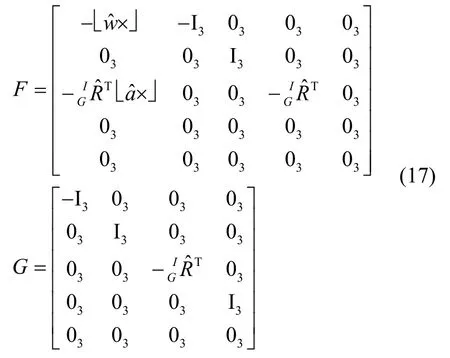
2.2 离散时间IMU 状态增广

传统的MSCKF 算法对离散时间IMU 状态增广，对式(10)采用数值积分法，使得每次积分都得引入当前位置到世界坐标系的旋转量，如图1所示，当对tk时刻相机位姿求导时，将会对图像帧之间所有IMU 状态求导，这将带来极大的计算量，因此本文采用1 节中论述的封闭解的IMU 预积分算法，替代数值积分法。

对离散时间IMU 状态估计值增广，从时间tk到tτ+1，通过零阶四元数积分得到旋转四元数；通过1 节中论述的IMU 预积分算法得到tτ时刻的IMU 位置和速度，方程如下：

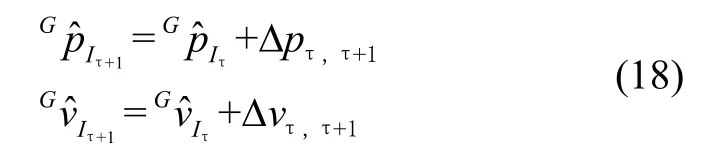
式中，Δp和Δv表示预积分项，如第1 节所示，通过当前IMU 测量值循环递归得到预积分项；且假设在［tτ,tτ+1］时间内，IMU 偏置的估计值保持不变，即：

2.3 离散时间系统协方差传播

离散式(16)系统离散时间状态转移矩阵和噪声协方差矩阵方程如下所示：

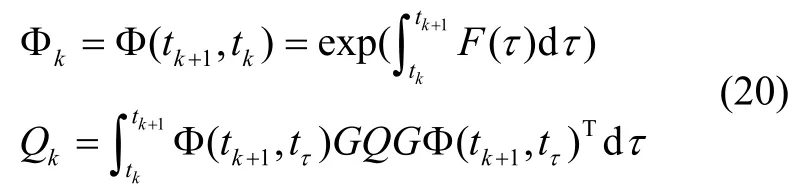
式中，Q=E[nI nIT]，表示连续时间系统噪声协方差矩阵；系统IMU 协方差矩阵传播方程如下：

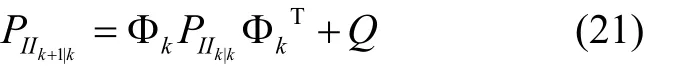
因此整个系统的协方差矩阵表达式定义为：

式中，PIIk|k为15× 15的IMU状态协方差矩阵；PCCk|k为6N×6N的相机状态协方差矩阵；PICk|k为IMU和相机相关矩阵。系统协方差矩阵传播方程为：

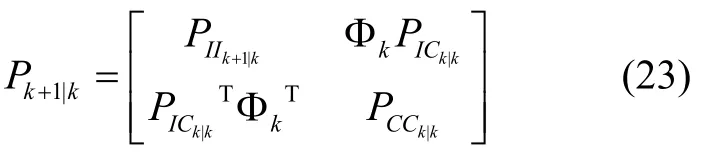
当系统接收到新的图像帧时，将其添加到系统状态向量中，此时相机的状态可以由IMU 状态和相机与IMU 之间的外参数计算得到，如式(24)：

式中，C（·）表示单位四元数到旋转矩阵的转换；表示IMU 和相机之间的旋转四元数，表示IMU 坐标系下相机的位置，可以由线下标定获得。此时系统的协方差矩阵增广形式如下式：

式中，J为相机状态方程对应的雅克比矩阵。

3 逆深度参数化观测模型

假设单个空间地图特征点fj，能够在连续的Mj帧中被单目相机观测到，相机的位姿向量分别为；则每个相机对此地图点的观测方程可以定义为：

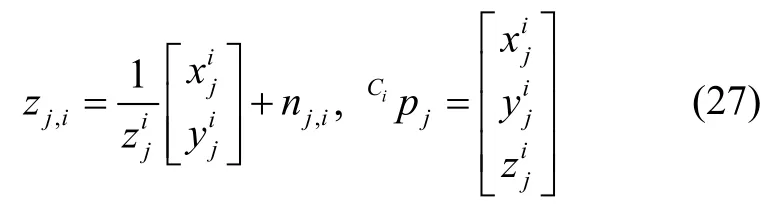
式中，nj,i表示相机观测噪声；Cipj表示地图点fj在相机Ci中的位置，其方程如下：

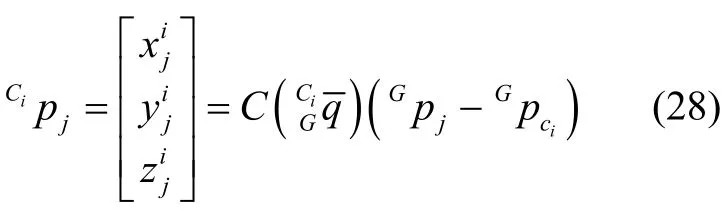
式中，Gpj表示地图点fj在世界坐标系中的位置坐标。

传统的MSCKF 算法使用式(27)作为相机的观测方程，当z 轴方向趋近于零时使得观测会出现奇点的情况影响系统的数值稳定性，本文对Gpj采用逆深度参数化方法，将有效避免MSCKF 算法的缺陷。其方程为：

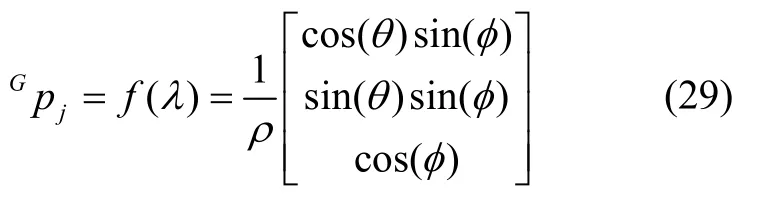
式中，λ=［θφ ρ］T；

系统的观测残差方程为：

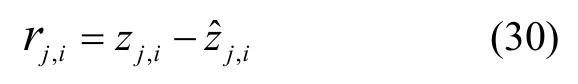
式(30)线性化可得：

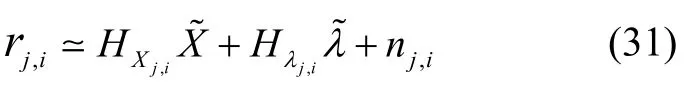
式中，HXj,i表示残差相对于系统误差的雅克比矩阵；表示逆深度参数λ的误差，可由测量值通过最小二乘法解出[17]；Hλj,i表示残差相对于参数的雅可比矩阵。

将式(31)扩展到对该地图点的所有的相机观测，即可得到该地图点的观测残差方程为：

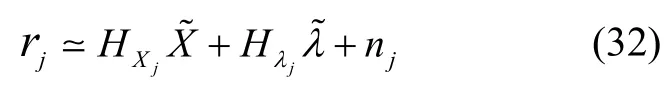
式中，HXj和Hλj为扩展后的协方差矩阵；nj为扩展后的噪声协方差矩阵；HXj、Hλj和nj都是由HXj,i、Hλj,i和nj,i组成的块矩阵或向量；由于在不同的相机观测中地图点特征是相互独立的，因此相机观测噪声向量nj的协方差矩阵可以定义为Rj=σ2im I2Mj。为了使观测方程能执行观测更新，将式(32)左乘Hλj的左零空间矩阵VT，定义残差，则：

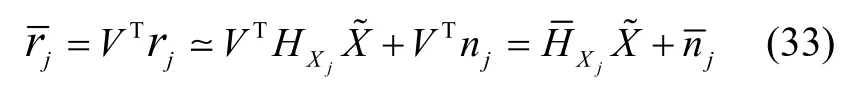
式中，VT为Hλj的左零空间矩阵，且：

由于矩阵Hλj的秩为2Mj× 3，因此其左零空间矩阵VT为秩2Mj- 3的酉矩阵，且观测噪声nj的协方差矩阵为：

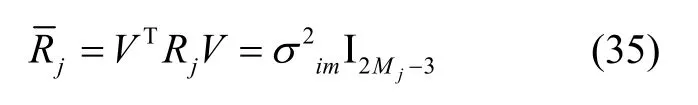
式(33)定义了对Mj个相机观测到的单个地图特征点的线性约束，充分利用了Mj个相机状态的观测信息，并且可以直接用于EKF 观测更新。

4 EKF 更新

假设时间k+1时，相机观测到M个地图特征点，则此时整个状态估计系统的观测残差可以由(j=1……M)扩增得到，定义系统残差为，则残差方程为：

式中，、和分别是由、和组成的块向量或者矩阵；系统残差r的维度为：

的噪声协方差矩阵如式(38)：

在实际应用中，即使M很小，其对应的残差维度d依然会是一个很大的值，这将导致非常大的系统计算量，为了减少计算量，让算法能够实时运行，在EKF更新之前对式(36)进行QR 分解；注意到为非满秩矩阵，对其QR 分解如下：

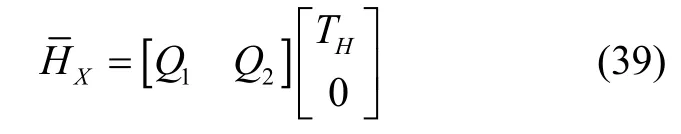
式中，Q1矩阵和Q2矩阵为形式唯一的酉矩阵，TH为上三角矩阵，将式(39)代入式(36)中，得：

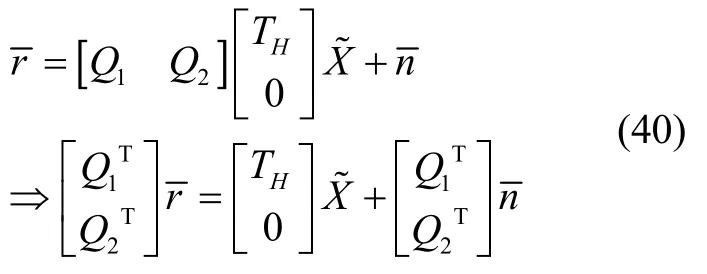
式中，由于项只包含测量噪声，可以忽略。所以式(40)可以简化为：

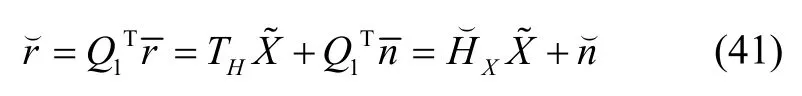
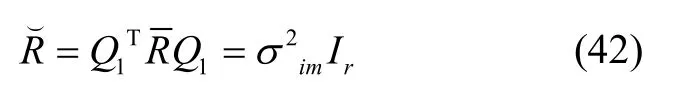
式中，r为矩阵Q1的列数。此时，系统卡尔曼增益矩阵为：

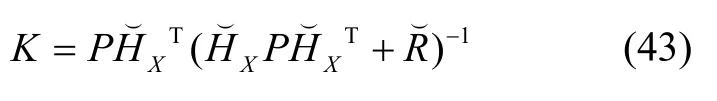
状态方程修正量为：

协方差矩阵更新方程为：

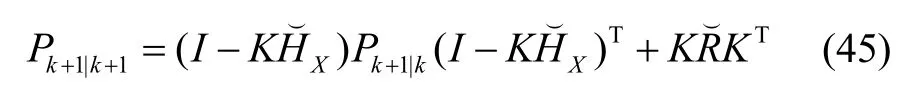
5 试验与结果分析

采用公开的EuRoc 数据集对本文提出的算法（后文记作proposed）进行性能分析。EuRoc 数据集包括从微型飞行器上收集到的11 个飞行序列数据。该数据集图像采集频率为20 Hz，IMU 采集频率为200 Hz，并且数据提供真实轨迹（后文记作Groundtruth）。本文试验使用内存为8 GB 的英特尔Core i5-8300H@2.30 GHz 四核笔记本电脑，将本文算法与MSCKF[1]和RVIO[13]两种算法比较。

为了验证本文提出的逆深度参数化方法相对于MSCKF 算法的稳定性，本文以EuRoc 数据集中的Vicon Room 中V2_01_easy 序列为参考标准，设计一组对比试验。试验中只改变MSCKF 算法更新步骤中的观测方程，分别采用标准MSCKF 算法和基于本文提出的逆深度参数化的MSCKF 算法，试验结果如图2所示。从图示的轨迹曲线可知，标准MSCKF 算法和逆深度参数化的MSCKF 算法整体上较为接近，但是在某些序列段中，逆深度参数化的MSCKF 算法跟真实的轨迹更为接近。通过查看数据集轨迹序列可知，该部分检测到的特征点Z 轴分量接近于零，使用逆深度参数化的MSCKF 方法具有更高的定位精度。

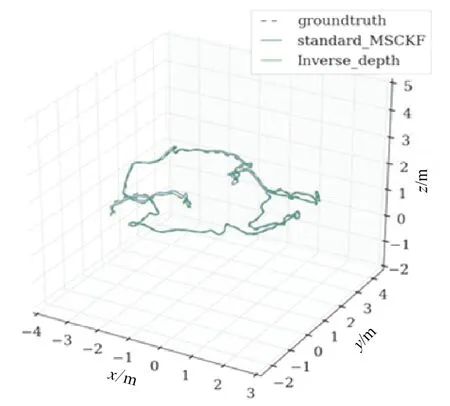
图2 V2_01_easy 序列轨迹Fig.2 V2_01_easy sequence trajectory

为了进一步分析逆深度参数化方法的性能，图3展示了试验轨迹在XYZ 三轴上的轨迹分量，由图3可知，标准的MSCKF 算法和逆深度参数化的MSCKF算法在X 轴和Y 轴上的轨迹较为一致，但是Z 轴方向上，逆深度参数化的MSCKF 算法跟真实参考值更为接近，性能提升较为明显。

为了验证本文提出的两点改进算法的有效性，将本文算法与MSCKF[1]和RVIO[13]两种算法比较。采用EuRoc 数据集中的Vicon Room 中的6 个飞行序列，并图示了V1_01_easy和V2_02_medium两个数据序列轨迹，分别如图4和图5所示。

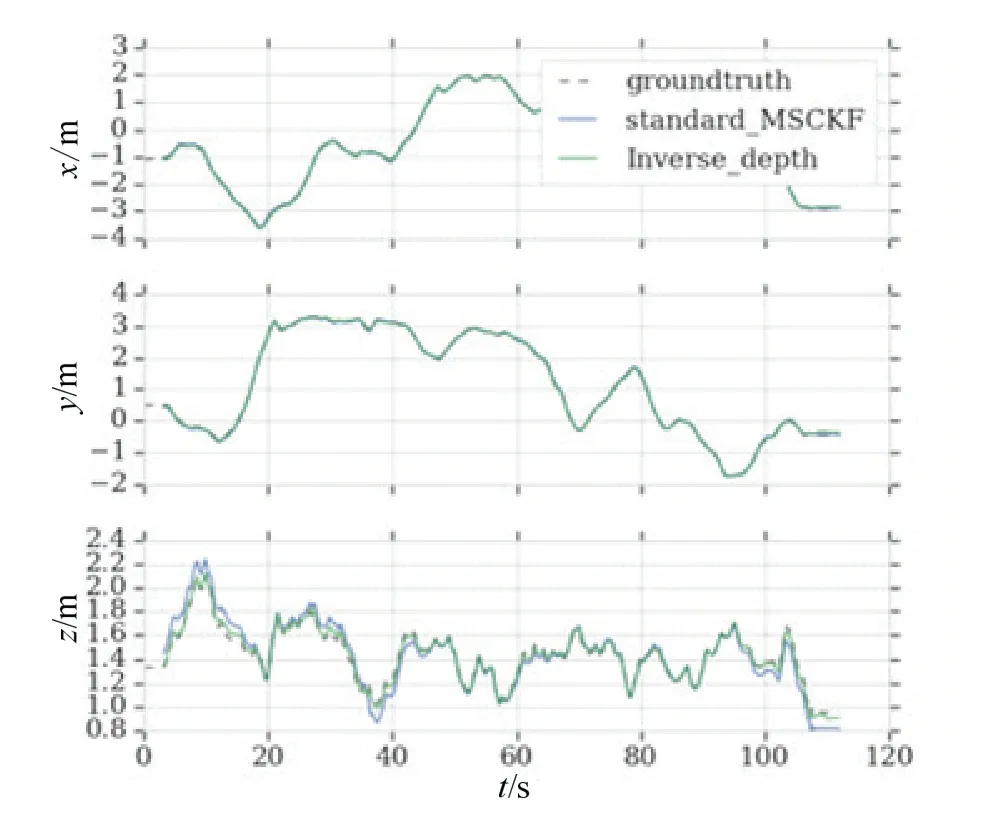
图3 X、Y、Z 三个方向运动轨迹与实际轨迹Fig.3 X、Y、Z movement trajectories and actual trajectories

由3 图中轨迹可知，MSCKF 算法轨迹与真实值轨迹偏离较大；RVIO 算法和本文提出的算法与真实值轨迹基本重合，但本文提出的算法轨迹更连续稳定，且偏离更小。

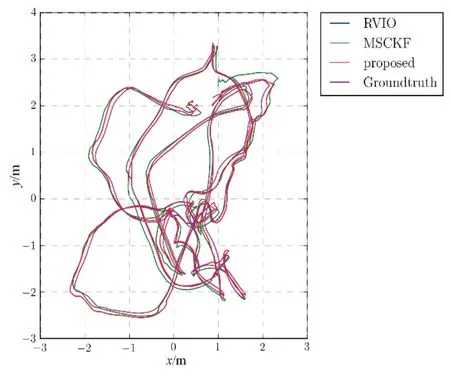
图4 V1_01_easy 序列轨迹Fig.4 V1_01_easy sequence trajectory

图5 V2_02_medium 序列轨迹Fig.5 V2_02_medium sequence trajectory

为了进一步分析算法的性能特性，本文以“V2_02_medium”数据集为例，对定位误差进行分析。“V2_02_medium”数据集是难度系数适中的数据集序列，收集数据的场景为一个房间，该序列运动速度适中，场景中有丰富的视觉特征，光度条件较好，可以保证准确地特征跟踪。图6为本文算法在X、Y、Z三个方向上轨迹漂移误差曲线，图7为本文算法中载体的俯仰、滚动和航向三个姿态角的误差曲线，图6为三个算法在X、Y、Z 三个方向上的运动轨迹与实际轨迹对比曲线。从图6和图7可以看出本文算法的位置漂移不超过0.15 m；俯仰角和滚动角漂移幅度较小，航向角误差相对较大。从图8可以看出MSCKF 算法在X、Y、Z 方向的漂移程度较大，而RVIO 算法和本文算法漂移程度较小，基本与真实轨迹重合。

为定量地分析本文算法的定位精度，表1对数据集6 个飞行序列上的估计结果的均方根误差（RMSE）进行了统计计算。表1将均方根误差指标最小值用加黑体字进行了标注。由标注结果可示，相对于其他两种算法，本文算法在其中4 个数据集上表现出更好的精度，且整体的均方根误差平均值表现出较好的精度，精度提升比较明显。由此可以说明本文算法相对于传统的MSCKF 算法或者RVIO 算法提高了定位精度。相较于传统的MSCKF 算法，其均方根误差减少了约36.5%。

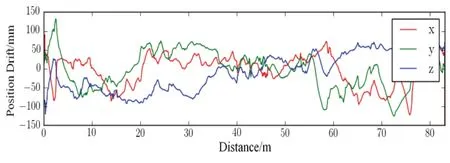
图6 X、Y、Z 三个方向上轨迹漂移误差Fig.6 X、Y、Z trajectory drift error

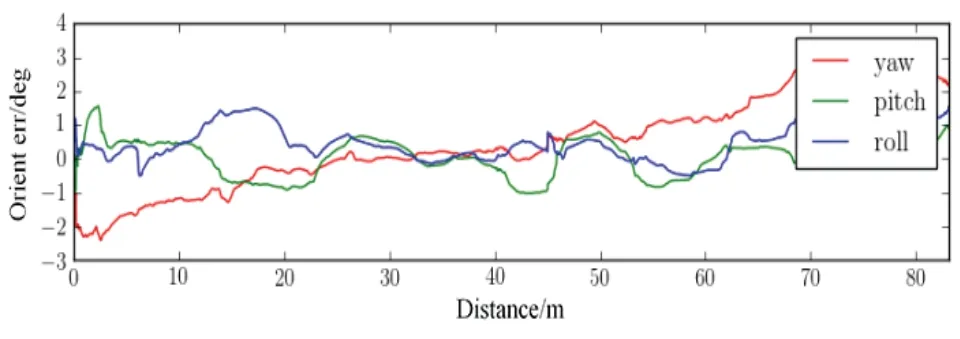
图7 俯仰角、滚动角和航向角漂移误差Fig.7 Pitch,roll and yaw drift error

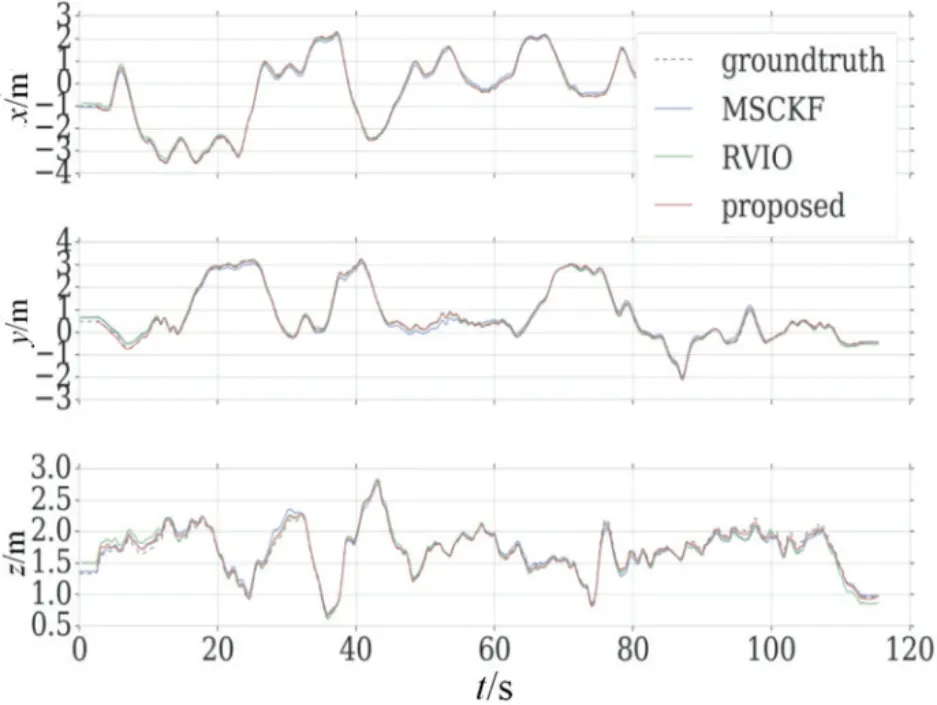
图8 X、Y、Z 三个方向运动轨迹与实际轨迹Fig.8 X、Y、Z movement trajectories and actual trajectories

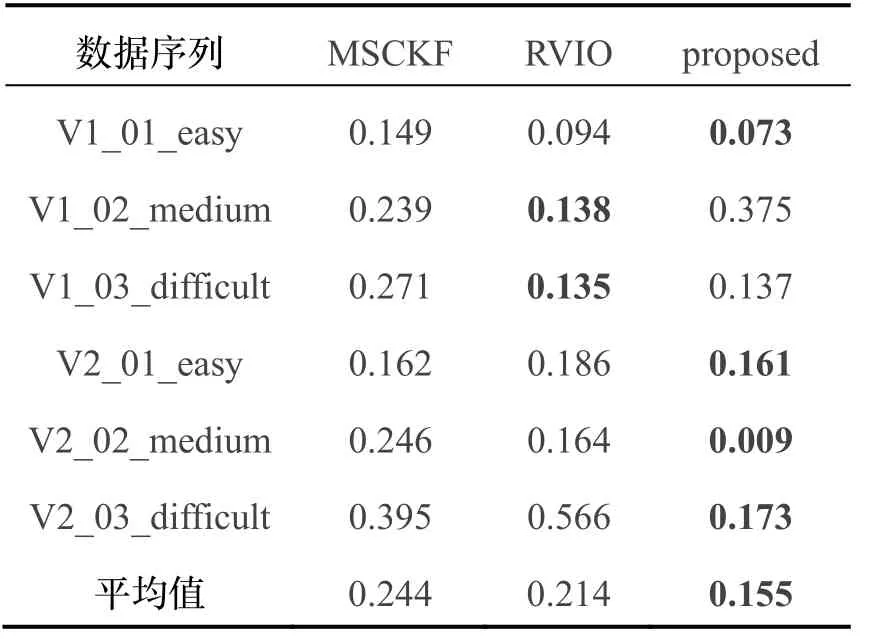
表1 EuRoc 数据集轨迹误差统计（单位：米）Tab.1 Statistical of trajectory error in EuRoc dataset (unit: m)

6 结 论

为了提高MSCKF 框架下的视觉惯性里程计系统定位精度和系统鲁棒性，本文对传统的MSCKF 算法做出了两点改进措施，并通过试验验证了算法的有效性。针对如何快速精确地处理两帧图像之间的IMU 数据的问题，提出了一种基于IMU 预积分封闭解的算法，相较于传统基于优化的视觉惯性里程计算法在分段常数加速近似下采用离散四元数积分来简化所需的预积分值，IMU 预积分封闭解算法在IMU 时间周期内求解解析解，并应用于MSCKF 视觉惯性里程计框架下，试验证明可以有效提高系统定位的精度。针对MSCKF算法观测方程参数化方法存在的数值稳定性的问题，提出了一种逆深度的参数化方法，该方法克服了MSCKF 算法在空间点坐标z 轴深度值趋近于零时，系统观测值会出现奇点的情况，试验结果表明，该算法相较于传统的MSCKF 算法，能有效增加系统的鲁棒性。

通过在公开的EuRoc数据集上试验验证了该算法的有效性，同时将本文建立的视觉惯性里程计算法与已有开源的视觉惯性里程计系统对比，在EuRoc 数据集六个飞行序列上的试验结果表明，改进的算法在定位精度和稳定性上均有提升，相较于传统的MSCKF视觉惯性里程计算法漂移较小，均方根误差（RMSE）减小约36.5%，定位精度得到有效提升。