一类切换时滞系统在异步切换下的绝对指数稳定性
2020-12-14贾红威王跃华
刘 娟, 贾红威, 王跃华
(沈阳大学 师范学院, 辽宁 沈阳 110041)
在许多科学和工程领域,如通信网络、制造系统、生物和其他领域等,时滞会经常出现,它经常会引起系统性能的下降甚至使系统不稳定.时滞系统的稳定性问题在近几十年得到了广泛的研究,并引起了许多学者的关注[1-4].在目前的研究中,切换非时滞系统或时滞非切换系统是相对简单的,切换与时滞同时存在的系统可能会变得更为复杂.事实上,切换时滞系统有着很强的实际背景,分布式网络、热交换系统和钻井系统等都是切换时滞系统.近年来,切换时滞系统引起了人们极大的兴趣[5-8].
绝对稳定性理论也是一个重要的研究方向,该理论由Lur’e首次提出.后来,许多学者开始研究这类含有非线性限制系统的绝对稳定性并有了很多结果[9-13].由于时滞在现实生活中的重要作用,近年来,这类时滞系统的绝对稳定性引起了越来越多专家和学者的广泛关注与研究.
尽管如此,到目前为止,以上对于时滞系统绝对稳定性的研究均是非切换的.实际上,含有非线性有界项的该类切换时滞系统具有广泛的应用.文献[11]考虑了该类切换时滞系统的绝对稳定镇定,给出了相应的控制器设计.但是,文献[11]给出的控制器切换与子系统切换是同步的.众所周知,到目前为止,控制器设计有2种方法.最初,控制器与子系统的切换被假设是同步的. 实际上,这种假设是不现实的.系统的切换过程是需要时间的,这个时间(切换时滞)就使得控制器间的切换以及子系统间的切换是异步的.
鉴于此,本文主要考虑了这种含有非线性有界项的切换时滞系统在异步切换下的稳定性.首先,得到了跟切换时滞有关的控制器设计;其次,本文的结果拓展了非切换系统及切换系统[11]的相关结果.
1 问题陈述
考虑如下切换时滞系统

(1)
式中:x(t)∈n,ω(t)∈m,z(t)∈m分别表示系统的状态向量、输入向量、输出向量;τ>0,是常时滞;φ(·)是一个连续的向量值初始函数;σ(t):[0,∞)→M={1,2,3,…,m}表示切换信号,表示第i个子系统被激活,m表示子系统的个数;Ai,Bi,Ci,Di,Ei,Fi均为适当维数的常矩阵;u(t)为控制输入向量;φ(t,z(t)):[0,∞)×m→m是非线性向量值函数,关于时间t处处连续,在z(t)处是全局Lipchitz的,且φ(t,0)=0,另外,φ(t,z(t))还满足
[φ(t,z(t))-K1z(t)]T[φ(t,z(t))-K2z(t)]≤0, ∀t≥0,∀z(t)∈m,
(2)
式中K1、K2为适当维数的常矩阵,并且K=K2-K1是对称正定矩阵, 此时,非线性函数φ(t,z(t))被称为属于向量[K1,K2].
假设在切换瞬间,系统的状态不发生跳变,并且,假设在有限时间区间内,仅仅发生有限次切换.在理想的情况下,当系统发生切换时,对应的切换器同步进行切换,即u(t)=Mσ(t)x(t).然而在实际运行的过程中,由于无法预知哪个子系统被激活,这个时候需要首先识别子系统,然后将数据信息传送至控制器,从而进行系统切换.可以发现,切换过程实际上需要花费一些时间,而正是这个时间往往会造成控制器的切换与系统的切换不是同步的,这个时间被称为切换时滞.此时整个闭环系统将进行异步的切换.因此考虑如下形式的控制输入:
u(t)=Mσ(t - τs(t))x(t).
(3)
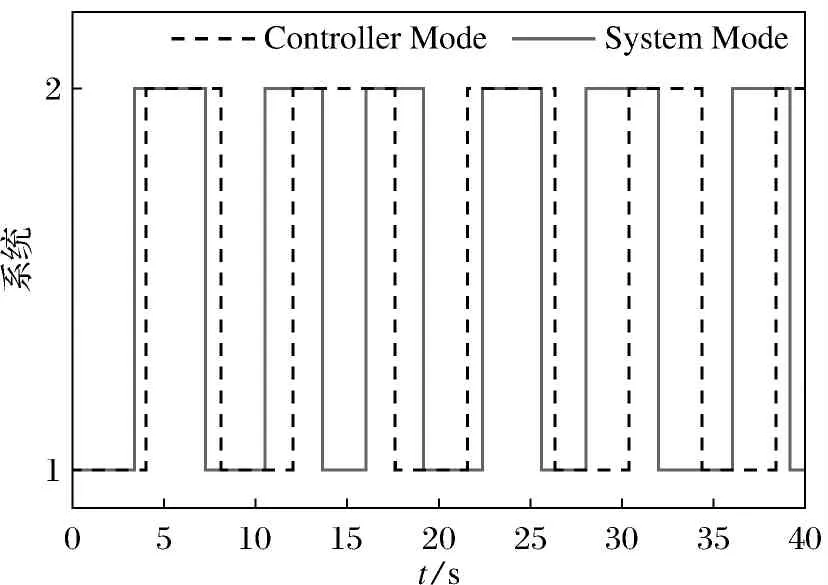
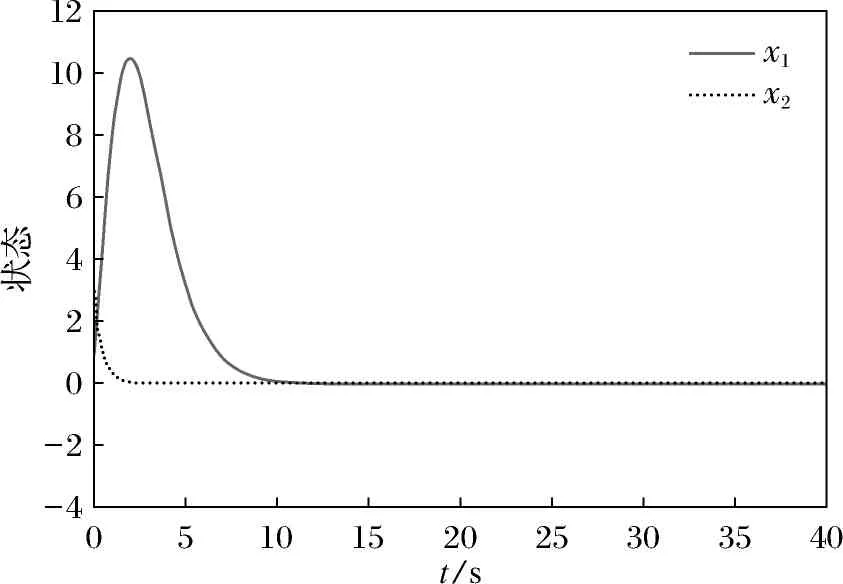
式中,τs(t):[0,∞)→[0,τs]是切换时滞,满足τs 这时对应的闭环系统为 (4) 下面给出本文中所需的定义及引理. 定义1[11]如果对于满足条件(2)的φ(t,z(t))以及某种切换信号,闭环系统(4)的零解是全局渐近指数稳定的, 就称式(1)在[K1,K2]上绝对指数稳定. (5) 那么,对于∀ξ≠0,ξTFiξ≥0,以下不等式成立 ξTF0ξ>0. (6) 特别地,当p=1时,式(5)与式(6)等价. 引理2[14]系统 (7) 在[K1,K2]上的绝对稳定性与系统 (8) 在[0,K]上的绝对稳定等价. 引理3[15](Schur补) 对于适当维数的矩阵Q=QT,S,以及R=RT,不等式 等价于下列2个不等式: R>0,Q-SR-1ST>0. 设计反馈控制器(3)以保证相应的闭环系统(4)是绝对指数稳定的.首先,当φ(t,z(t))∈[0,K]时,得到如下定理. (9) (10) 式中: 那么控制器(3)可以保证系统(4)在任意满足如下平均驻留时间 (11) 证明 利用信号整合的方法,设计切换信号σ′(t)=(σ1(t),σ2(t)),σ′(t):[0,∞)→M×M.由于切换时滞的存在,当第j个子系统被切换到第i个子系统时,控制器Kj,即Ki-1仍然运行.此时会得到如下闭环系统: (12) 选取Lyapunov-Krasovskii函数如下: (13) 沿着式(4)的解的轨迹对Vi,i(t)关于时间t求导得: (14) 式中, 类似地,沿着式(4)的解的轨迹对Vi,j(t)关于时间t求导得: (16) 式中, 由式(1)及φ(t,z(t))∈[0,K],得 ωT(t)ω(t)+ωT(t)K[Dσ(t)x(t)+Eσ(t)x(t-τ)]≥0, (17) 从而 这时,如果存在实数ε≥0,使得以下不等式成立: 于是根据引理1可得: ηT(t)Σi,iη(t)<0,ζT(t)Ξi,jζ(t)<0, (21) 则 事实上,式(19)与式(20)可以分别改写成 (24) (25) 式中: 式中, 此时,由Schur补定理,式(26)及式(27)分别等价于式(9)与式(10),从而式(22)与式(23)成立. 下面证明式(4)的绝对指数稳定性. 当t∈[tk,tk+τs(tk)[,k∈+时,由式(23)得到 当t∈[tk+τs(tk),tk +1],k∈时,由式(22)得到 令 (31) 则 a‖x(t)‖2≤V(t)≤b‖x(t)‖2. (32) 于是, 注1 本文选取的Lyapunov-Krasovskii函数与控制器的切换信号有关,使得异步切换下的控制器设计与分析变得更为简单. 注2 事实上,当τs(t)=0时,相应的切换即为同步切换,此时定理1将退化为文献[11]中的定理2. 当φ(t,z(t))满足一般的条件(2)时,可以得到如下推论. 式中 Λ11、Θ11、Θ14、Θ24、Θ33如定理1中所示. 证明 利用引理2及定理1,容易得到本推论. 切换系统(1)中的参数如下所示: 此时,相应闭环系统的切换信号及状态反应曲线分别如图1及图2所示. 图1 异步切换信号Fig.1 Asynchronous switching signal 图2 闭环系统的状态反应曲线Fig.2 State response curve of closed loop system 本文考虑了一类含有非线性项的切换时滞系统在异步切换下的绝对指数稳定的状态反馈控制器设计.所考察的绝对指数稳定性指的是扰动输入在一定区域内取值时,系统的零解在某种切换信号下均是指数稳定的. 绝对指数稳定性概念拓展了有关切换时滞系统的其他稳定性概念. 首先,构造了适当的Lyapunov-Kracroskii函数,并设计了基于ADT的切换信号;然后,在此切换信号的基础上,进行了依赖于切换时滞的控制器设计,以保证闭环系统的绝对指数稳定性;最后,给出了结果的数值模拟与仿真,验证了结果的可行性与优越性.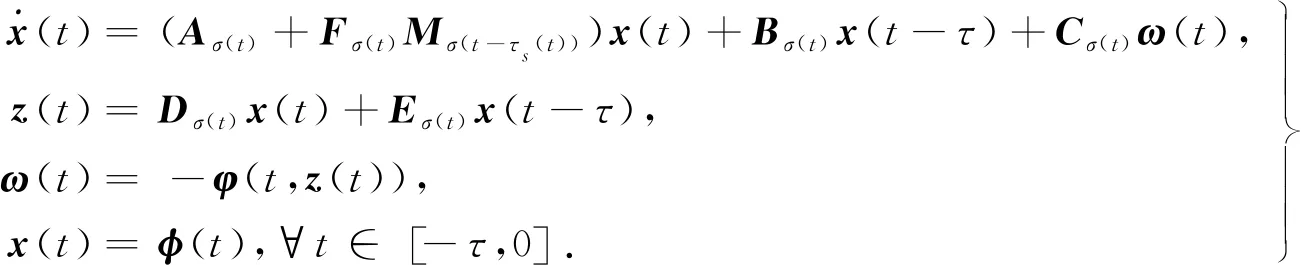
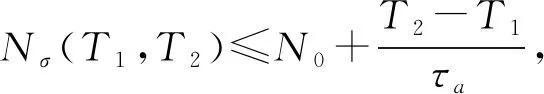


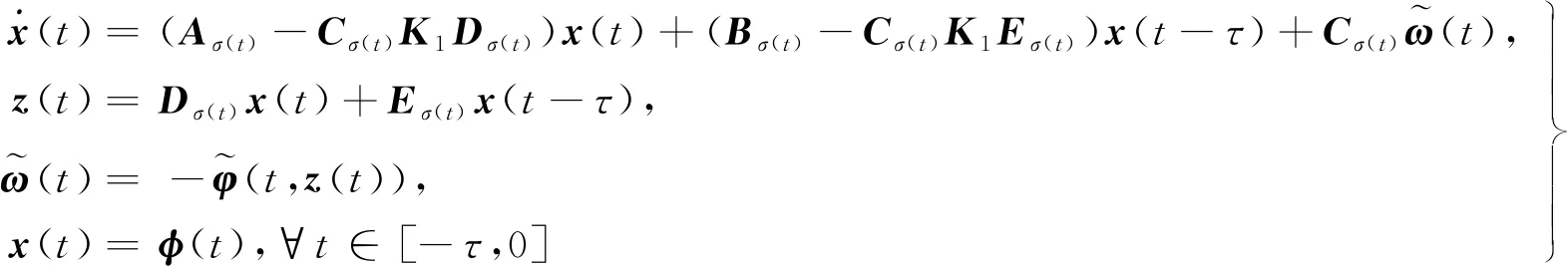
2 主要结果

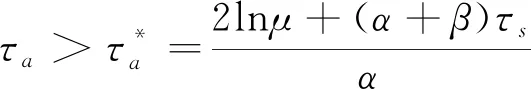

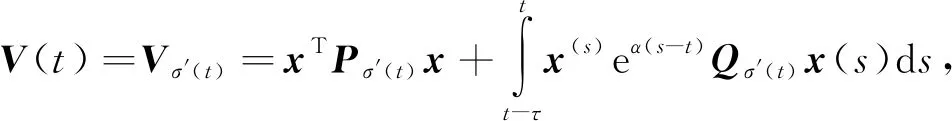




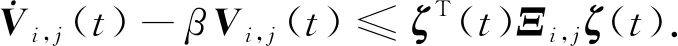
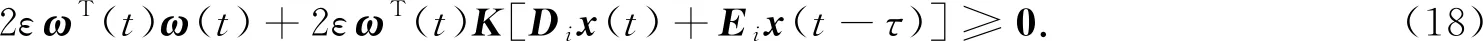
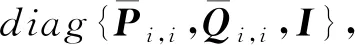

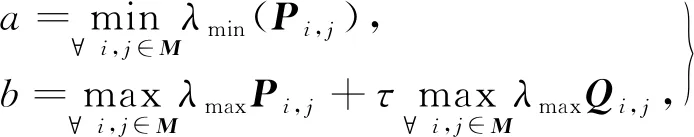

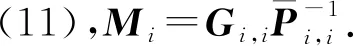
3 数值模拟与仿真
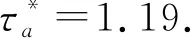
4 结 论
