核心素养下的小学数学生本课堂的构建

彭娟华

（福建省武夷山市崇安小学，福建武夷山 354300）

引 言

核心素养的提升是当前各学科教学中教师的主要任务，但每门学科都有其自身所对应的素养，目的就是确保学科价值及学科教学目标的最大化实现。所以，我们要借助生本课堂的构建来从不同的角度培养学生的数学学科素养，笔者从数学学科素养入手，结合生本课堂的构建来充分发挥学生的课堂主体地位，进而确保学生的数学学习能力得到大幅度提高。

一、生本课堂：数学抽象意识的培养

抽象意识是相对于形象意识、直观意识而言的，所以，随着生本理念的落实，我们要提高学生的数学课堂参与度，通过学生自主寻找数量与数量、图像与图像之间的关系等来帮助学生理解相关的数学概念，最终为学生抽象意识的形成，以及数学素养的提升奠定坚实的基础[1]。

例如，在教学“三角形分类”这部分知识时，为了构建有效的生本课堂，也为了培养学生的数学抽象意识，在教学时，笔者先让学生自己动手画出“所有”的三角形，这里的“所有”是指学生自己能够想到的三角形类型，同时，让几名学生在黑板上画出来，之后，与学生一起对这些图形进行归类，然后，对每类三角形的特点进行学习，如锐角三角形的角有什么特点，直角三角形的角有什么特点，等边三角形的边有什么特点等。之后，教师再组织学生思考等边三角形与锐角三角形之间有什么关系等，进而帮助学生对三角形的分类有一个明确的认识，同时，也能充分发挥学生的课堂主体作用，使学生在自主学习的过程中树立自主探究的意识。可见，在这样的教学过程中，直观的三角形绘制既可以降低单一讲授的枯燥感，又提高了学生的课堂参与度，之后的总结及归纳则是抽象出概念的过程，这对学生抽象意识的培养、学生数学素养的提升都起着非常重要的作用。

二、生本课堂：数学逻辑思维的培养

什么是数学逻辑思维呢？经过对相关文件的学习及实践经验的积累，我们认为可以借助归纳、类比及一般到特殊的推理来达到掌握知识的目的。同时，学生在积极参与这些活动的过程中，其数学逻辑思维也会得到培养，而且，这样的过程对生本课堂的构建也具有一定的推动作用。

例如，在教学“小数的加减法”这部分知识时，为了逐步培养学生的数学逻辑思维，也为了培养学生的类比意识，在教学时，笔者先组织学生对整数的加减法进行回忆，并列出几个式子，如51+28=___；89+53=___；58-27=___；53-26=___等，之后，让学生求出这些整数加减法的结果，并思考：5.1+2.8=___；8.9+5.3=___；5.8-2.7=___；5.3-2.6=___等，尝试结合教材内容对这些小数的式子进行求解，并推理出小数加减法的运算规律及小数加减法的本质，以强化对这部分知识的认识。可见，在这样的类比及同类思考的过程中，教师既可以凸显学生的课堂主体地位，有效落实以生为本的教育理念，又能帮助学生理解小数与整数之间的关系，进而培养学生的数学逻辑思维。

三、生本课堂：直观想象能力的锻炼

培养学生直观想象能力是为了建立数与形之间的关系，在构建数学直观模型中帮助学生理解和解决相关的数学问题。所以，作为一线数学教师，我们可以尝试组织学生借助图形来理解相关的数学知识或者是寻找题干中的数量关系，以此来为学生数学学习质量的提高打好基础。

例如，小红从家到学校，先走了3 分钟，每分钟的速度是80 米，但是，如果按照这种速度走的话，小红到学校会迟到3 分钟，所以，小红改为用110 米/分钟的速度行走后面的路程，结果提前到了3 分钟，问小红家到学校有多远？

这是一道小学数学教学中的典型性行程问题，也是数形结合的一类代表问题，从题干来看，数字比较多，而且数与数之间还存在一定的联系。所以，笔者先组织学生对该题进行了分析，明确了该题的考查点及其中的等量关系，即路程=速度×时间，之后，组织学生根据题干一步步绘制与其相匹配的图（见图1）。

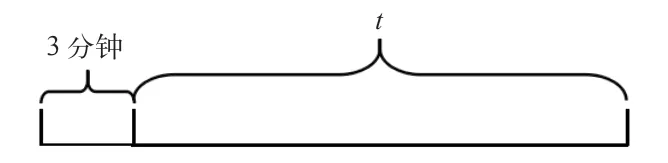
图1

从这样的图形制作的过程中，学生可以轻易地发现时间上的关系，即t+3、t-3，准确地设置出未知数，并找到等量关系来列方程，从而准确地解答出该题。当然，除这种数形结合的解题方法外，随着年级的增长，教师可以借助几何的直观想象及对学生空间能力的培养，来逐步培养学生的数学直观想象能力。

四、生本课堂：数学建模能力的形成

数学建模是数学学科素养中的重要内容之一，但在实际教学中，我们常常会考虑现阶段学生学习能力的问题而不对学生进行建模教学，导致很多学生的知识运用能力有限，尤其是当数学与实际生活进行联系时，很多学生都不能从中分析出数学知识，找不到联系点。所以，在构建生本课堂的背景下，教师要转变思想，注重对学生数学建模能力的培养，进而为学生数学能力的发展打好基础。

例如，一个长方形的操场，长为60m，宽为30m，校长想对其进行扩建，即将宽增加10m，如图2 所示，思考：扩建后的操场面积有多大？

该题对于学生来说相对较为简单，但为了培养学生的建模能力，也为了帮助学生理解数学运算定理，在解答的过程中，笔者组织学生先对该题进行绘图，之后，根据直观的图形来找到等量关系。学生在思考的过程中提出了两种解题思路，即

方法一：60×(30+10)=2400（m2）

方法二：60×30+60×10=2400（m2）

图2

方法一运用的就是长不变、宽变的方式，整体的思路还是长×宽=面积。而对于方法二来说实际上原来的面积+增加后的面积，求的是面积和。计算到这里，教师不妨引导学生进行建模，既然两种方法得出的结果是一样的，我们可以组织学生将两等式左边的式子分别转到等式的左边和右边，即60×(30+10)=60×30+60×10，60×30+60×10=60×(30+10)，引导学生观察式子，最终得出结论，即乘法分配律。可见，在这样的一个建模过程中，学生可以自己体会整个推导过程，不仅能够提高相关知识的理解能力，还能强化认识，提高学习效率。

结 语

综上可以看出，数学学科素养的提升对学生数学学习能力的培养、对学生知识运用能力的锻炼都起着非常重要的作用。但前提是学生自主参与，积极成为课堂的主体，也就是说，我们要充分发挥生本课堂的作用，通过组织恰当的活动，来全面提升学生的数学学科素养。