基于修正Theta法的P92钢蠕变行为及寿命预测研究

叶有俊，王志成，王一宁，张鹏鹏，姜 勇

（1.江苏省特种设备安全监督检验研究院，江苏 南京 210036；2.南京工业大学，江苏 南京 211816）

近年来，随着资源与环境问题的日益严峻，火力发电机组的蒸汽参数在不断提高[1-2]。P92钢是一种添加了Nb、V和W等元素改良得到的新型Cr-Mo耐热钢，其综合性能优异，已逐步成为超超临界机组主蒸汽管道的重要用钢[3-6]。然而在高温、高压的长期服役过程中，P92钢不可避免会发生蠕变损伤，造成构件失效[7-10]，因此对其进行寿命预测研究势在必行。文中通过对P92钢进行蠕变试验，利用修正Theta法对蠕变数据进行分析，以研究P92钢的蠕变行为及寿命预测。

1 P92钢蠕变试验试样及试验条件

蠕变试验中使用的试样为P92钢构件，其管件尺寸为Ø390 mm×70 mm，实际操作压力26 MPa，操作温度 600℃。依据 GB/T 2039—2012《金属材料 单轴拉伸蠕变试验方法》[11]加工恒载荷蠕变试验试样，其形状与尺寸见图1。为了避免试验数据分散，试样材料均从同一根尚未使用的P92钢管上截取。

图1 恒载荷蠕变试验试样形状和尺寸

综合考虑P92钢构件的实际操作温度与实际操作压力，蠕变试验温度选取650℃，应力分别为180、165、135、115、100、90 MPa。

2 修正Theta法简介

Evans R W和Wilshire B等[12-15]提出了Theta projection concept蠕变数据处理方法 （简称Theta法），该方法适用于预测不同温度及应力水平下材料的蠕变性能，Theta投影法示意见图2。

图2 Theta投影法示图

Theta法表达式为：

式中，εt为总应变；t为蠕变时间，h；et为试验曲线和拟合曲线之间的随机误差；θ1为描述蠕变第一阶段的应变硬化参数，θ2为描述蠕变第一阶段的应变速率，θ3为描述蠕变第三阶段的应变弱化参数，θ4为描述蠕变第三阶段的应变速率。参数θi（i=1，2，3，4） 是与应力 σ 和温度 T有关的参数，且满足以下关系式：

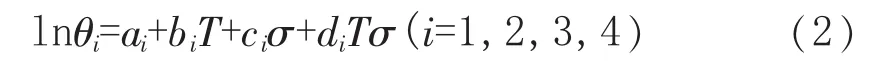
式中，ai、bi、ci和 di为材料常数，可以通过最小二乘法对短时蠕变数据进行多元线性回归得到具体的数值。

当4个材料常数确定后，通过式（1）和式（2）可得到任意温度和应力状态下的材料蠕变曲线，从而可以通过高应力、高温度条件下的短时试验数据预测低应力和较低温度下的蠕变曲线，进而推导出材料的蠕变寿命。对式（1）进行求导可以得到最小蠕变速率表达式：

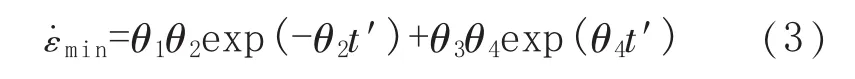
对蠕变曲线进行分析时发现，Theta法存在一定的不足，某一时刻与其后一时刻之间的误差值呈现出一定的线性关系，致使式（1）中的随机误差值et不满足互不相关性条件。因此，由Theta法得到的拟合曲线与实际试验曲线之间吻合程度不高，使得参数θi具有一定的不确定性。赵艳萍[16]将N阶自回归模型应用于Theta模型中，对传统的Theta法进行了修正，建立了修正Theta模型，以此来消除上述不确定性。修正Theta模型具体表示如下：

式中，ert为时间为t时的误差；vt为与自相关性无关的新误差；N为回归阶数；ρi为相关系数，主要用于描述自相关度，可以通过式（5）拟合得到。

通过式（5）可以计算得到误差值最小的vt，按照此值得到的蠕变试验曲线与拟合曲线之间的吻合程度更高。

3 P92钢蠕变试验结果与讨论

3.1 蠕变曲线分析

P92钢在650℃不同应力下的试验蠕变曲线见图3。

图3 650℃不同应力下P92钢的试验蠕变曲线

由图3看出，不同应力下P92钢蠕变主要由蠕变第二阶段和蠕变第三阶段组成，蠕变第一阶段时间非常短，第二阶段蠕变速率较为稳定，而第三阶段蠕变速率不断增加。随着应力的增大，蠕变更快进入第三阶段，蠕变断裂时间相应急剧缩短。当应力为90 MPa时，蠕变断裂时间在6 000 h左右；当应力提升至180 MPa时，蠕变断裂时间急剧缩短为50 h左右。

650℃下P92钢蠕变断裂时间和应力之间的关系曲线见图4。由图4可以知道，蠕变断裂时间和应力呈现近似线性关系，其结果符合以下指数形式：

式中，tr为蠕变断裂时间，h；A、P为参数，均可通过最小二乘法拟合获得。

图4 650℃下P92钢蠕变断裂时间与应力关系曲线

最小蠕变速率是描述材料蠕变性能的重要参数，也是计算许多其他蠕变参数的基础。650℃下P92钢最小蠕变速率与应力关系曲线见图5，与断裂时间关系曲线见图6。

图5 650℃下P92钢最小蠕变速率与应力关系曲线

图6 650℃下P92钢最小蠕变速率与断裂时间关系曲线

从图5和图6可以看出，在对数坐标下，最小蠕变速率与应力σ和断裂时间tr之间均呈现较好的线性关系。

式（7）为Norton公式，可以表示最小蠕变速率与应力的关系：

式中，n为应力指数，B为材料参数。最小蠕变速率与蠕变断裂时间在双对数坐标下同样呈现线性关系，利用经典的Monkman-Grant公式[17-20]即可描述两者之间的关系：

式中，α、C均为材料参数，通过最小二乘法线性拟合即可获得。

利用式（7）和式（8）可以对P92钢在蠕变试验中的寿命进行预测，但传统Theta公式法存在一定的局限性，外推的寿命不能太长，仅可预测最长试验时间10倍以内的寿命，故后续研究中采用修正Theta法模型进行蠕变行为和寿命的预测。

3.2 修正Theta法预测材料蠕变行为及寿命

结合实际蠕变数据和修正Theta法模型，利用数理统计软件Eviews分别对650℃下，应力为100、115、135、165 以及 180 MPa 时的 P92 钢蠕变曲线进行拟合，得到了ln θi与施加应力σ之间的关系曲线，见图7。

图 7 650℃下 P92钢的 ln θi与 σ 拟合曲线

由图7可知，P92钢的参数 θi的对数与应力σ之间线性相关，具体关系式见表1。

表1 650℃下P92钢参数 θi与应力关系式

利用表1中的关系式，可以得到修正Theta法下 650℃、90 MPa时 P92钢的 θi值， 将 θi代入式（5）拟合得到P92钢蠕变曲线，从而进行寿命预测。利用传统Theta法和修正Theta法得到的650℃、90 MPa下P92钢的蠕变试验曲线拟合值和随机误差见图8。从图8可以看出，传统Theta法和修正Theta法均可以较好拟合得到材料的蠕变曲线。传统Theta法得到的随机误差曲线呈现典型的波浪状分布，表明由该方法得到的结果具有自回归性，修正Theta法得到的随机误差值明显减小，进一步验证了修正Theta法的准确性。

图 8 650℃、90 MPa下利用 Theta法和修正 Theta法得到的P92钢蠕变试验曲线拟合值及随机误差

图9 基于修正Theta法P92钢最小蠕变速率预测值与实测值比较

利用最小蠕变速率进行预测时，蠕变速率实测值与利用修正Theta法得到的预测值之间的相对大小可以用来确定预测精度，两者之间的比较见表 2。

由表2可以看出，两者之间最大误差为22.99%，在允许的范围之内[21-22]。

表2 基于修正Theta法650℃下P92钢最小蠕变速率预测值与实测值比较

4 结论

（1）P92钢蠕变曲线主要由蠕变速率较为稳定的第二阶段和蠕变速率随时间增加的第三阶段组成，蠕变第一阶段时间非常短。蠕变应变随着应力的减小而不断减小，随着应力的增大，蠕变断裂时间也相应急剧缩短。蠕变断裂时间与对应应力呈现近似线性关系，可为后续构件的寿命评价提供一定的参考。

（2）利用修正Theta法与传统Theta法对P92钢蠕变曲线进行拟合的结果表明，修正后的结果与试验数据吻合度更高，误差更小。计算所得ln θi值与应力σ之间具有良好的线性关系，修正Theta法得到的θi值具有较高的可靠性，为后续外推数据及预测各参数奠定了基础。