粗糙集理论下的海量数据挖掘算法

刘福刚

（淮南联合大学信息工程学院 安徽淮南 232001）

一、基于粗糙集数据挖掘步骤

随着信息技术、计算机技术的发展，信息展现出指数上升的增长速度，也出现大量数据库，涉及银行存款、制造业等领域，信息量迅速增长，导致传统分析方法难以达到现实需求。应对海量数据，如何充分挖掘有价值的数据或者知识，是一项艰巨的任务，必须提供一项去伪存真的技术。数据挖掘则是一种具有强大功能、潜在的技术，可以帮助用户自海量、隐含的数据内找出重要、有价值的信息，从而预测未来的行为，有利于用户做出准确的决策。数据挖掘作为近些年数据库领域研究的新兴热点，也成为提升管理决策支持能力重要的手段及工具，其主要任务在于由大量数据内提取未知、隐含有价值的知识。数据挖掘研究热点也从单一的数据挖掘转变为多种方法结合起来获取知识[1-4]。本研究提出依托粗糙集开展数据挖掘的方法，粗糙集理论用于处理海量数据，从而消除一系列冗余信息。粗糙集理论就是用于研究不完备、不精确信息处理的重要工具，其研究对象是具备多个属性描述的一组对象集合，并把对象以等价关系为依托在整个空间实施划分，从而划分成正域、负域及其边界[5-7]。其特点就是由实际数据入手，不再依赖对象模型，无需先验知识，结论也是客观的。自波兰数学家首次提出粗糙集相关知识后，通过几十年的研究及发展，该理论在实际应用方面获取长足进展，也受到不同领域的广泛重视及关注。粗糙集理论就是创建在分类机制上，将分类理解为在特定空间内的等价关系，这种关系就是对空间实施划分，旨在利用已有知识库，把不确定或并没有精确的知识通过已有知识库内的知识进行近似划分。如今，粗糙集理论在人工智能、故障分析、决策支持等方面得到成功的应用。采用粗糙集相关理论，对一般信息系统执行数据挖掘，其步骤如图1所示。具体操作步骤如下：（1）数据抽取：自数据库或数据表内，依托合并、聚合等手段，在海量数据内提取相关数据，组成相应的数据集；（2）预处理：把数据集合内非数值属性列实施编码处理，补齐缺值，组成数值化数据集。离散化：把处于连续状态的属性值展开离散化处理，最终组成决策表[8-13]。属性约简：对第3步形成的决策表展开属性约简操作，删除冗余属性及其不必要性，求解属性核。对属性约简之后决策表内的冗余属性值执行删除处理，提取精炼、有效的规则知识；规则解释：对数据提取后，将各条规则属性值翻译成没有编码或离散化前的描述。粗糙集理论主要特点如下：不得不说，粗糙集方法比较简单、实用，它在创立后迅速得到应用，其具有下列特点：粗糙集理论支持处理各类数据，包含不完整数据、具有多变量数据；它可以处理数据不精确性，包含确定性与非确定性这两种情况；它可以求出知识的最小表达及知识不同颗粒层次；它可以由海量数据内揭示概念简单，方便操作的模式；它能够产生精确、便于检查、证实的规则，尤其适合用在智能控制规则自动生成过程中[14]。

二、基于动态聚类两步离散化算法

这种算法就是运用动态聚类算法对决策表实施离散化处理，随后，依托断点重要性算法进行第二次离散化处理，以此获取相应的断点集。依托粗糙集数据挖掘算法发现规则需要经过下列步骤，见图1。先把数据库中的初始数据转变成为粗糙集形式，明确设定条件属性及决策属性；在属性约减环节，组成不可分辨的矩阵，并在设计的矩阵上生成约减属性集；在响应的约减信息表内，依据可信度阀值准确发现规则[15]。

图1 基于粗糙集的数据挖掘处理实现简图

（一）改进处理的离散化算法。

算法1：

输入相应的决策表S=

输出：S首次进行筛选操作后，断点集CUTfirst循环历经S每一个条件属性k，算法执行如下：

（1）对k的每个断点重要性进行求解，并遵循自小到大的原则对断点值实施排序，把求解出来的结果保存到数组Importantk[]内，m表示重要的断点所处数组位置，即：

初始化聚类个数为1，循环控制变量为v=e+1；

若v>e，需要执行下列循环操作：

建立聚类中心表T，处在l-h范围之内自Importantk随机选取k个初始聚类中心；假设循环变量e1=0，如果e1≠v，执行以下操作：

①e1=v；

②对T中每种类数值与Importantk每一个h-l距离进行统计，并将上述统计结果同类到距离最小的类别中；

③对于聚类中心处于T中各类别数据实施调整；

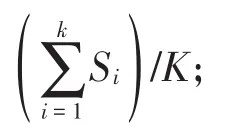
（2）K=K+1；

（3） 在l=m+l，h=|Importantk|-1,n=|h-l+1|，执行第3步至第5步。

自每一个聚类内挑选最重要的断点添加至CUTfirst内。

决策表通过以上算法离散化后，其效果仅次于依托属性重要性离散化算法的局部离散化效果。下文把CUTfirst输入到断点重要性算法中开展第一次全局离散化处理，以此获得依托动态聚类的两步离散化算法。

（二）两步离散化算法。

算法2：输入：S=

输出：S断点集CUTfirst；

算法操作流程：

（1）在并未实施离散化条件下，计算S的正区域POSC(D);

（2）对算法1进行调用，获取CUTfirst；

（3）通过断点集CUTfirst对S展开初步离散化处理明确S1正区域数值，假设S1代表离散化处理后的决策表，若不成立，实例会被CUTfirst划分为等价类集合采用L代表，对每一个X∈L，做出下列处理；如果以上条件成立，可以转至第5步。

（8）如果每个X∈L，且当Cmax等价类X划分为X1、X2，将等价类添加至L内，并由L中将X去掉；

（9）若L内所有等价类实例均不具备一致的决策，需要转移至第3步；反之，所有算法操作完成。从算法2视角分析，如果数据集中包含许多候选断点，此时，这种算法需要执行较长的运行时间，要结合并行计算思想对算法实施再次改进。

（三）两步并行离散化算法。

在算法3中，输入：S=

输出：决策表S断点集CUTlast，算法执行步骤为：

（1）在没有实施离散化条件下，求解出S的正区域POSc(D)；

（3）在并行处理中，若设当前进程是Pi，Pi依据算法2对Si内每个条件属性的候选断点展开聚类处理。如果设定聚类后的断点集是CUTfirst i，发送CUTfirst i至主进程；

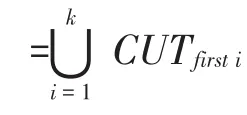
（5）进行断点补充修复阶段，与算法2相同；

（6）在断点散播环节，断点集CUTlast自各进程L代表的实例划分为相应的等价类集合，CUTlast=Φ，L={ }U。

由进程P1对CUT1这个断点集实施处理，···，Pk对CUTk进行处理；

（8）在并行处理环节；假设当前进程是Pi，Pi求解CUTi内每一个断点c重要性WCUTlast(c)，选定断点至主进程P1；

（9）对于每一个X ∈ l，在等价类X被划分为X1、X2，并将X1、X2添加至L内，并将X去掉；如果L内全部等价类内的实例均不具有相同的决策，需要执行第2步，反之，则算法结束。

三、算法测试结果分析

（一）改进Rough Set算法正确性及可伸缩性。挑选UGI数据库内的5个数据集，对比通过CDL改进的只是约简算法与原始算法的正确性，结果如表1所示。根据该表数据可知，采用CGL改造之后的知识约简算法并不影响原始算法的正确性、识别率等各项性能。

表1 对比不同算法正确性

在训练集由10万条逐渐增加导致100万条状态下，测试集记录的数据就是整个训练集30%。在此基础上，组成海量数据集，其包括条件、决策属性分别为8个、1个，其结果如图1所示。根据下图可知，新改进算法能有效提升算法可伸缩性，促使其适应更大的数据集。与此同时，这种算法具有良好的性能，不失具备正确率及识别率。对知识发现需要使用大量的时间，与测试所用平台配置的SQL服务器效率存在密切的关系，运用并行算法能提升其处理速度。

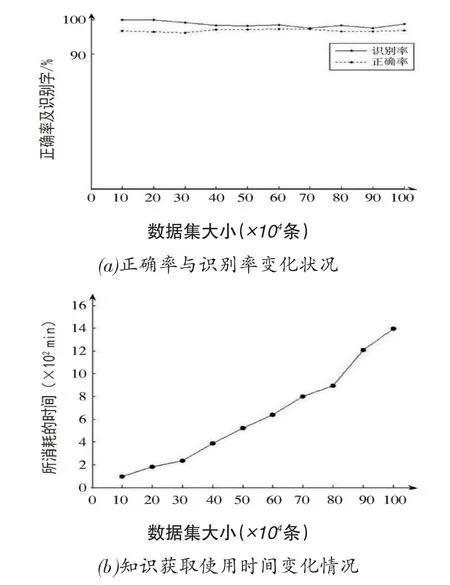
图1 改进算法测试结果分析

（二）基于动态聚类两步离散化算法并行化处理。根据UCI数据库挑选6组数据集对算法2展开测试，其中，算法运行时间采用T代表，规则集正确识别率以P代表。采用基于动态聚类的离散化算法实施动态聚类处理后，其结果如表2所示。自SONA、IRIS等方面分析，每一个数据集候选断点数据均明显降低下降。而基于动态聚类提出的两步离散化算法计算速度较快，从正确识别率等方面分析，贪心算法、基于断点重要性、动态聚类的算法处在一致状态[16-18]。

表2 离散化处理后断点个数

四、结语

综上所述，基于最常应用的数据挖掘算法，依托类分布链表对传统算法实施改进处理，这种改进算法有利于直接处理海量数据，进而实现处理超大规模数据集这个目标。系统依托并行化求解思想，借助并行离散化算法明确类分布链表方法，进而解决系统内存有所限制的问题，提升所用算法运行效率。