基于康奈尔笔记法的根轨迹教学方法研究

王立国，刘 丽

（哈尔滨工业大学a.电气工程及自动化学院；b.化工与化学学院，哈尔滨 150001）

0 引言

根轨迹法是“自动控制原理”教学中的重要内容之一［1-2］。根轨迹向上承接控制系统建模、方框图化简、传递函数分析，向下与Nyquist判据频域分析、Bode图的相频特性分析相印证，因此讲清楚这部分内容十分关键。但由于根轨迹是开环系统某一参数从零变化到无穷大时，闭环系统特征根在s平面上变化的轨迹，其绘制规则多达10 条，涉及渐近线、出射角、入射角、与虚轴的交点、分离点及根轨迹增益等多个概念的有机融合［3-7］，初学者对此多有困惑，难以把握根轨迹的学习实质，因此探究一种使学生易于理解的根轨迹教学方法十分关键。

康奈尔笔记法由康奈尔大学的Walter Pauk 博士［8］提出，此方法问世以来，已在生物学教学、深度阅读、英语报刊阅读、化学教学、临床医学教学、高职计算机课程学习及大学英语听力理解中得到成功应用［9-13］。康奈尔笔记法又称为5R笔记术，以Keywords（关键词）、Notes（注解）及Summary（概括）为主要特征，包括Record（记录）、Reduce（简化）、Recite（背诵）、Reflect（补充）、Review（复习）5 个阶段［14-17］，尤其适用于根轨迹概念烦冗、思路复杂及综合性强的解题过程。

本文以康奈尔笔记法为出发点，以哈尔滨工业大学-伊顿联合实验室为依托，针对根轨迹教学及实践教学中存在的问题，从教学理念、教学内容、教学方法等实践环节方面进行改进。依据康奈尔笔记法将根轨迹法适用的稳定性分析、暂态性能分析及稳态性能分析进行5R归纳，总结为闭环传递函数分析、闭环极点的实部与虚部、闭环极点与坐标原点的距离、闭环极点与负实轴的夹角、主导极点、增加开环极点对根轨迹的影响等典型的关键词，注解其作用与实质，并将其概括系统特征根在s平面移动对控制系统稳定性的影响。所做工作有助于学生对根轨迹内容的深入理解，促进了“自动控制原理”这一课程与国际知名院校的接轨。

1 康奈尔笔记法

康奈尔笔记法是一种集笔记、复习、自测和思考于一体的学习方法，以5R为特征；其精髓在于基于笔记本三栏区间划分，将课前预习和自测相结合，快速、准确地进行课堂记录，从而提高学生课堂学习的效率。康奈尔笔记法示意图如图1 所示，核心在于记录、简化、背诵、补充与复习。

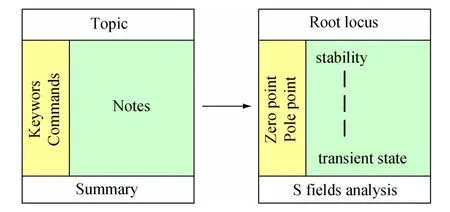
图1 康奈尔笔记法示意图

1.1 Record（记录）

Record（记录），在最大的笔记栏（Notes）中先进行快速直接的记录与收集。

（1）根轨迹的基本概念。根轨迹：当系统开环传递函数中某参数（如根轨迹增益）在某一范围内（如）连续变化时，闭环特征根在s平面上移动的轨迹，称为根轨迹。知识点总结见图2。

（2）根轨迹学习的前期知识点（见图3）。开环传递函数：前向和反馈通道的传递函数的乘积，G（s）H（s）；闭环传递函数；特征方程：1 ＋G（s）H（s）＝0；

系统的开环增益K，根轨迹增益Kg；开环传递函数的零点／极点；闭环极点及特征根等。

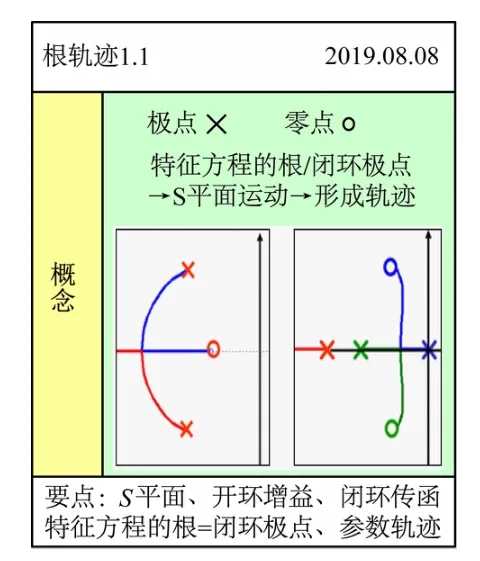
图2 根轨迹的基本知识点总结

图3 根轨迹学习的前期知识概括

1.2 Reduce（简化）

Reduce（简化），提炼重点，专注于获取关键词、关键语句，以便跟上授课速度，之后查缺补漏。

（1）根轨迹学习的必要性。基于特征方程应用Routh判据进行稳定性分析时，是通过Routh 表，利用特征方程根与系数的关系进行定性分析，得到的只是稳定、临界稳定、失稳3 种定性状态，难以定量分析系统稳定性；根据系统特征根可以定量分析稳定性，但特征根往往难以直接求出，因此亟须探求一种可行的稳定性定量分析方法。这是根轨迹法学习的初衷，如图4 所示。图4 表明，根轨迹法实质在于根据系统的开环零极点来分析系统的闭环极点／特征根的特性，属于图解方法，核心在于分析开环零极点随着系统参数的变化在S平面发展趋势及规律，可以部分定量分析控制系统的稳定性。

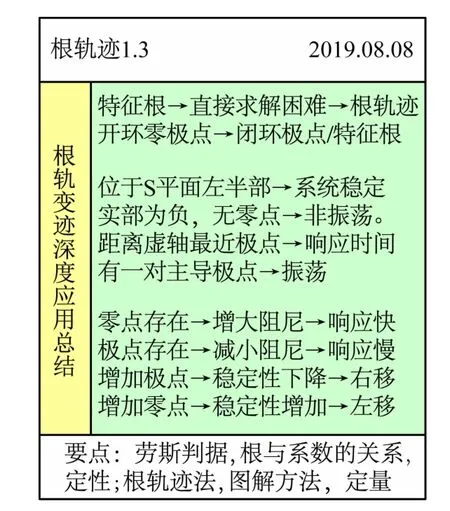
图4 根轨迹特性的简化分析

（2）根轨迹分析特点。①闭环极点位于S平面左半部，系统稳定；②闭环极点实部为负，无零点，非振荡；③闭环极点有一对主导极点，振荡；④响应时间取决于距离虚轴最近的极点；⑤零点的存在，增大阻尼，响应快；⑥极点的存在，减小阻尼，响应慢；⑦增加极点，稳定性下降，根轨迹右移；⑧增加零点，稳定性增加，根轨迹左移。

1.3 Recite（背诵）

Recite（背诵）：透过重点与资料的对照，转化出可以执行的学习行动。突出内容的实质与深度，力求精简，方便记忆。根据讲义，根轨迹的绘制规则总结为：①Rule ＃1，根轨迹的起点和终点。②Rule ＃2，实轴上的根轨迹。③Rule ＃3，根轨迹的对称性和渐近线。④Rule ＃4，渐近线和实轴的交点。⑤Rule ＃5，根轨迹的出射角和入射角。⑥Rule ＃6，根轨迹与虚轴的交点。⑦Rule ＃7，根轨迹的分离点。⑧Rule ＃8，分离点（多重）根轨迹方向夹角。⑨Rule ＃9，在某特定点上的根轨迹增益K。⑩Rule ＃10，闭环极点之和。

对上述规则应用康奈尔笔记法进行记录整理，如图5 所示。

图5 根轨迹绘制规则背诵笔记总结

图5 中将根轨迹绘制规则总结为点、线与面（角）：①点，涵盖起点与终点（Rule ＃1），交点（Rule ＃4，Rule ＃6，Rule ＃7），极点之和（Rule ＃10），特定点上的根轨迹增益（Rule ＃9）。②线，涵盖实轴上的根轨迹（Rule ＃2），渐近线（Rule ＃3）。③面／角，出射角和入射角（Rule ＃5），分离点（多重）根轨迹方向夹角（Rule＃8）。

图5 计算的难点在于出射角和入射角：①出射角——指起始于开环极点的根轨迹在起点处的切线与正实轴的夹角。②入射角——指终止于开环零点的根轨迹在终点处的切线与正实轴的夹角。

1.4 Reflect（补充）

Reflect（补充）：对根轨迹整体策划有了了解后，与刚刚学习过的动态性能指标分析相比总结，补充系统动态响应与稳态响应之间的对应关系，具体如图6所示。

根据图6，动态响应与稳态响应关系，可定量地总结为如下几点：

（1）动态性能分析，闭环极点的实部反映系统的调整时间，负实数极点离虚轴越远，对应的分量衰减越快，系统的调节时间就越短，响应越快。

（2）闭环极点与负实轴的夹角β反映了系统的超调量。

图6 稳态响应与动态响应关系总结

（3）稳定性分析，闭环极点在S左、右平面的分布反映了系统的稳定性；根轨迹全部位于S 平面的左半侧，且距离虚轴越远越稳定。

（4）闭环极点的虚部表征系统输出响应的振荡频率。

（5）闭环极点与坐标原点的距离表征了系统的无阻尼自然振荡频率。

（6）当系统具有多个闭环极点时，可借助于主导极点的概念，将系统简化成低阶系统。

（7）系统稳态误差的大小与系统的开环增益成反比，开环增益与根轨迹增益之间存在比例关系。

（8）增加开环零点，可使根轨迹向左半S 平面弯曲或移动，增加系统的相对稳定性，增大系统阻尼，改变渐近线的倾角，减少渐近线的条数。

（9）增加开环极点，可使根轨迹向右半S 平面弯曲或移动，降低系统的相对稳定性，减小系统阻尼，改变渐近线的倾角，增加渐近线的条数。

（10）由已知的开环零、极点的分布及根轨迹增益，通过图解法找出闭环极点。一旦闭环极点确定后，再补上闭环零点，系统性能便可以确定。

（11）由于闭环特征根和系统开环传函有相关性，因此改变开环传函的参数可以达到改变系统性能的目的。

1.5 Review（复习）

Review（复习）：这样一则以康乃尔笔记法写成的课堂记录与笔记，可以让学生事后回顾与查找资料时更容易找到重点。核心在于总结关键词，尽快从笔记本中提炼出关键思想和关键事实，把浓缩后的要点记录在左手边的那一栏。关注那些关键的字词和那些最为重要的概念。

绘制根轨迹的基本规则（见图7）源于相角条件和幅值条件，可将根轨迹的起点和终点、实轴上的根轨迹、根轨迹的渐近线、渐近线和实轴的交点、出射角和入射角、根轨迹与虚轴的交点、分离点、分离点（多重）根轨迹方向夹角及某特定点上的根轨迹增益及闭环极点之和统一于相角条件和幅值条件之下。

图7 根轨迹绘制规则与响应参数归纳

在综合分析根轨迹分析对系统动态性能与稳态性能分析的基础之上，对系统的校正做出延伸与预测，为教材的第6 章（超前、滞后及期望校正）奠定理论分析基础。

（1）增加开环零点对根轨迹的影响。①改变渐近线的条数和渐近线的倾角。②相当于增加微分作用，使根轨迹向左移动或弯曲，提高相对稳定性，过渡过程时间缩短；③增加的开环零点越接近坐标原点，微分作用越强，系统的相对稳定性越好。

（2）增加开环极点对根轨迹的影响。①改变渐近线的条数和渐近线的倾角。②相当于增加积分作用，使根轨迹向右移动或弯曲，从而降低了系统的相对稳定性。系统阻尼减小，过渡过程时间加长。③增加的开环极点越接近坐标原点，积分作用越强，系统的相对稳定性越差。

2 实例分析

实例：某系统开环传递函数为式（1），试绘制以为α变量的参数根轨迹，并讨论系统的稳定性。

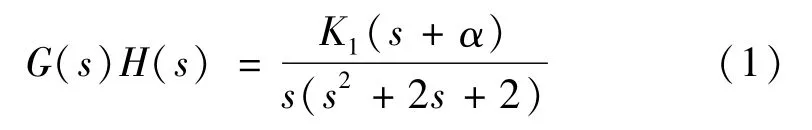
应用康奈尔笔记法求解过程如图8～12 所示，按照根轨迹绘制规则来进行，突出角度的大小与方向选择；注意虚轴左侧系统稳定；虚轴右侧，失稳；根轨迹与虚轴交点，系统临界稳定。

图8 等效（参数）特征方程的推导

图9 开环零极点、实轴上根轨迹

图10 根轨迹的渐近线相关计算

图11 与虚轴交点的相关计算

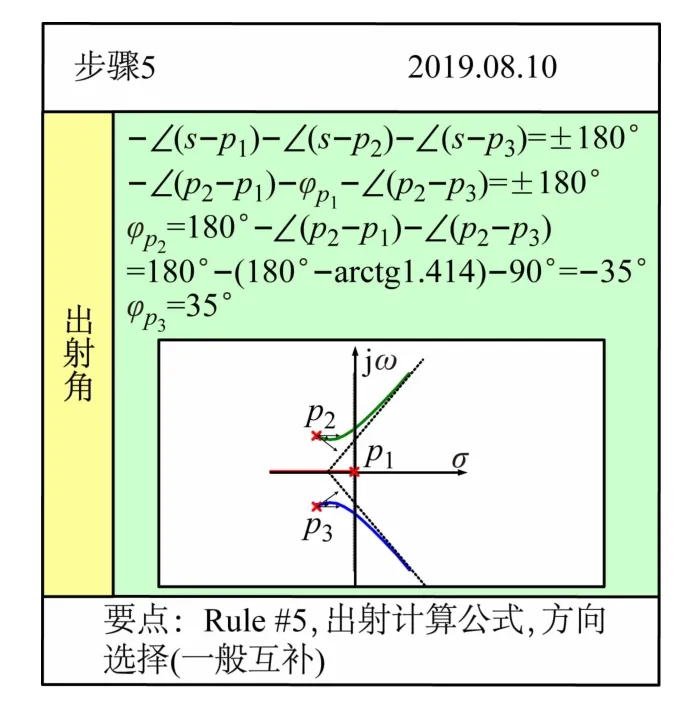
图12 出射角的相关计算

图8～10 分析中，注意应用Rule ＃1～Rule ＃4 时与幅值条件、相角条件结合起来，实际上根轨迹分析过程时刻与幅值、相角相关。

3 结语

基于美国康奈尔大学笔记法思想，将其与“自动控制原理”教学中的根轨迹法有机结合，建立根轨迹10 条绘制规则与康奈尔大学笔记之间的逻辑教学体系，突出记录、简化、背诵、补充与复习5 个环节教学内容、教学方法的改进；以哈尔滨工业大学-伊顿联合实验室为依托，提出了具有哈尔滨工业大学电气工程教学特色的康奈尔大学笔记法思路。

2018 年9 月，将康奈尔大学笔记法思想融于“自动控制原理”双语教学中，突出图1～7 所示的教学体系模式。重点对15 个同学的笔记／作业进行观察、总结及改进，取得了较为理想的授课效果。现在这15 人有14 人以保研的资质进入硕士学习阶段（课题进展顺利）、其中1 人的“自动控制原理”结业考试成绩为满分（100 分）；未取得保研资格的学生（1 人）后来自己考研成功。这在一定程度上验证了所提康奈尔大学笔记法教学思想的有效性。