连续深度基准面构建及通航水深服务模式研究
2020-12-11胡英俊张安民张佳丽侯泽北
胡英俊,张安民,2,张佳丽,侯泽北
(1.天津大学 海洋科学与技术学院,天津 300072;2.天津市港口环境监测工程技术中心,天津 300072)
水深是船舶安全航行中最关键的要素,水深测量以及通航水域动态水深的发布是航海动态信息服务最重要的内容之一。但是海水的瞬时深度受天文、气象等因素变化的影响,我国大多数海区受这些变化影响较大(孟德润等,1993)。国际海事组织(International Maritime Organization,IMO)为提高海上货物运输的高效性和安全性,于2006 年提出了e-航海概念(Graff,2009;IMO,2013),其中如何在航行中获得高精度的实时动态水深信息是各国研究的一项关键内容。在沿岸海域,尤其是船舶航行在接近安全航行水深的海域时,充分利用潮汐的有效水位,可提高航道通航能力、降低航程及船舶能源消耗,减少海洋环境污染(杜佳芸,2018)。
深度基准面是由验潮站的验潮资料利用调和分析法求得,采用13 分潮模型计算(海军司令部,1998)。因此深度基准面相对于平均海面数值,仅是对真正曲面形态基准面在特定点的采样,是离散、跳变和不连续的,具有区域性(柯灏,2012;暴景阳等,2013)。随着港口建设、船舶大型化和航运经济的迅猛发展,现有的深度基准面精度不高的问题成为制约海洋测绘服务于现代航运的瓶颈问题。此外,无验潮水深测量等远距离快速海道测量技术成为海洋测绘发展的主要方向,而这些技术发展的基本前提就是建立覆盖全海区的、高精度、无缝连接、平滑过渡的深度基准面。深度基准面构建方法依赖于潮汐的分潮理论,深度基准面的变化随潮波传播特征的变化而变化,如果能更深入地了解潮波运动特征,将对构建连续深度基准面具有指导作用。目前,国内已经有很多对于潮波的数值模拟研究,通过POM,FVCOM 等模式可以对研究海区的潮波运动进行较高精度的模拟(许军等,2008;张安民 等,2018;柯灝 等,2018;管明雷 等,2017;Lai et al,2018),已有学者采用POM 海洋模式模拟了渤海潮汐的主要特征(康鸿轩 等,2016)。而国外也已进行了相关研究,将潮波数值模拟的方法运用于保障船舶的航行安全,并取得了较好的效果(Chen et al,2013,2015;Lecci et al,2015)。
陆地高程基准和深度基准的不统一,导致陆海高程数据存在缝隙(周兴华等,2017)。建立一套具有通用意义的陆海高程基准统一方法和模型,是满足迅猛增长的测绘服务的需要。随着GNSS 空间大地测量技术的进步和高精度地面控制网络的完善,采用三维地心坐标系统已成为国际潮流,我国于2008 年7 月1 日启用了CGCS2000(China Geodetic Coordinate System 2000) 坐标框架即多源空间大地测量技术融合的组合框架(柳根等,2019)。张安民等(2013) 提出了基于CGCS2000参考椭球面构建陆海一体化的垂直基准并建立数字球 模 型, 以 GNSS(Global Navigation Satellite System)为主要定位手段可实现一体化地形更新和水下地形更新的模式。将深度基准面值归算到CGCS2000 参考椭球面上,构建陆海高程一体化测绘基准,可以满足日益多元化的测绘服务需求,同时以CGCS2000 参考椭球面作为深度基准面具有计算简单、易于转换的特点,符合未来发展方向。本文在此基础上对通航水深相关的基准面及其相互转换进行了讨论,提出釆用数值模式进行高精度连续深度基准面的构建方法,应用POM 模式,建立基于参考椭球面的动态海面模型。通过高精度GNSS直接进行海底地形测量,并通过基于参考椭球面的深度基准面模型和海底大地高的差值获得海图水深及通航水深。
1 通航水深相关垂直基准面及其转换关系
1.1 平均海面
平均海面是指某地在一定时间段内的海面变化算术平均值,可由验潮站观测数据计算算术平均值得到。这种方法获得的平均海面值是离散、跳变的,精度不高。而卫星测高数据可提供大范围、全天候的水位变化观测数据。通过卫星获取某种平均意义上的海平面相对于参考椭球面的大地高,即海平面高度。融合多源卫星测高数据各项订正后可以精确刻画平均海平面高。
1.2 深度基准面
深度基准面通常为海图水深的起算面,在数据处理、水深测量、信息发布以至航海的过程中发挥着重要作用。深度基准面构建标准应是可以使船舶安全航行保障率达到95%以上。其作为海道测量和海图水深的垂直基准面,一般指的是位于平均海平面以下的一个面。其与平均海平面之间的距离,即L 值,随着各地潮差的不同而不同,一般都定在当地最低潮附近,潮差大的海区比潮差小的海区深度基准面低。因此,海图水深受深度基准面的计算精度的影响较大。
深度基准面利用调和分析法计算求得,由M2、N2、Q1、K2、S2、K1、O1、P1这8 个分潮叠加可能出现的最低值计算得到。《海道测量规范GB 12327—1998》(海军司令部, 1998) 中规定计算采用13个分潮模型,全部附加M4、MS4、M6的浅水改正和S4、Ssa的长周期改正,其公式为:
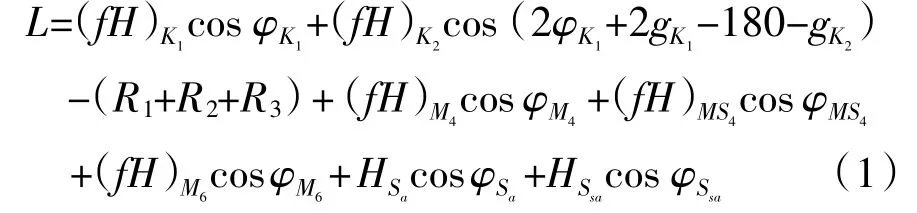
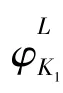
1.3 不同基准面间转换关系
与水位记录零点相关的潮汐基准信息在传统观测的方法中,是由验潮站水位观测数据的分析计算得到,进而通过验潮站大地联测数据实现与高程基准的联系,反映离散验潮站点的垂直基准转换关系(暴景阳等,2016)。而随着卫星测高技术的发展,垂直基准模型向着更大区域和高精度方向快速发展。海上航行相关的海图水深、各种高度与相关基准面之间的关系如图1 所示。
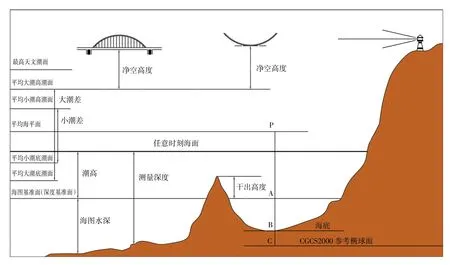
图1 各基准面之间的关系
孙翠羽(2011) 归纳了参考椭球面、平均海面、大地水准面和深度基准面等几个基准面的特点。其中参考椭球面具有数学表达严格、空间变化规则、符合GNSS 的使用、可直接测量参考椭球的大地高等优点,能够实现直接大地高测量,缺点是它不完全符合地球的物理特性,无法保障船舶的安全航行,不利于提高水深利用率,与海图高的使用习惯不相符合。
2 基于潮波模拟的深度基准面构建
2.1 研究方法
深度基准面推算模型构建有两种方法,其一是通过验潮站多年观测数据的离散点内插完成,其二是通过潮波动力学数值模拟的方式完成。第一种方法要求有一定密度的且布置合理的潮位站网点,这种方法成本高昂,并且受制于内插模型的适用性,深度基准面模型误差较大。本文采用的潮波运动数值模拟的方法不仅可以得到各点逐时的潮位变化情况,同时还能够得到模拟区域内各格网点的潮流流速、流向。通过一段时间的模拟潮位可进一步计算出各格网点处的潮汐调和常数,进而根据深度基准面模型构建整个海区的连续深度基准面。
2.2 模式介绍
POM 模式是由Alan Blumberg 和George L Mellor等人于1977 年创建(George,2004;Blumberg et al,1987;Ezer,2004),后由普林斯顿大学和美国国家大气海洋局地球流体动力学实验室等部门联合推广。
该模式的垂向混合系数由二阶湍流闭合模型确定,在很大程度上去除了人为因素的干扰,为提高模式计算效率,该模式应用时间分裂的算法。包括热力学的过程(李冬等,2010),使用静力近似。为了进一步提高模拟的精度,采用Blending 同化法(许军,2008)将实际观测数据融合到动力学模型中。Blending 同化法是指将实际卫星测高数掘直接插入到动力学模型中,把待求格网点的预报潮高看成是实际观测数据与动力学模型的模拟位的加权和的形式,其算法模型可以此公式表达:

如果控制点的潮汐参数是真值,则f 应取0.25 ~0.4,其主要起松弛调节作用。但T/P 存在3~4 cm的综合测高误差,同时调和分析得到的振幅基本具有等精度,而迟角的精度则不均匀,基本反比于分潮振幅,这使得f 的取值应小于1 且与分潮的平均振幅大致成比例。
2.3 研究区域及模型配置
模式计算域选取范围为37毅N—41毅N,117.5毅E—122.8毅E,水深数据来自TOPO2 卫星数据,近岸地区使用中国航海保证部出版的海图和实测水深进行调整,各网格点的潮汐调和常数数据来自俄勒冈州立大学发布的海潮模型(http://volkov.oce.orst.edu/tides/YS. html),模式水平分辨率为1.2忆伊1.2忆,模式网格格点数为200伊265伊13,由13 个分潮组成:M2、K2、S2、O1、Q1、P1、N2、K1、M4、MS4、M6、Sa和Ssa。其中,Sa和Ssa分潮由T/P 沿轨结果和沿岸验潮站结果利用Kriging 法分别内插正弦分量和余弦分量得到,其他分潮由数值计算得到。由POM 模式分别运行Q1、O1、P1、K1、N2、M2、S2、K2等8 个分潮,开边界与T/P 点的输入都对应单分潮的水位。浅水分潮也同时运行,此时开边界与T/P 点的输入为MS4、M2、S2、M4与M6。垂直方向上分为13个sigma 层,较好地拟合了海底地形和海岸线,可以较好地反映真实的地形。海底地形和海岸线形状对近岸潮汐的变化特征具有非常重要的影响,为直观表征模拟区域的地形特征,模拟区域的地形和水深分布(图2)。
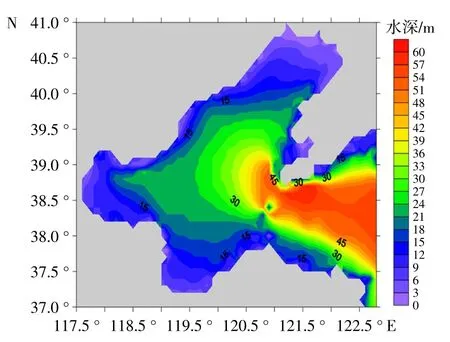
图2 模拟区域地形及水深分布
模式的内模式时间步长取60 s,外模式时间步长取2 s,模式运行480 h,最后48 h 每小时输出一次水位场,通过最小二乘调和分析法得到计算域内各网格点上的潮汐调和常数。M2、K1、O1和S2分潮同潮图如图6 所示,迟角采用东8 区。
2.4 模拟结果分析
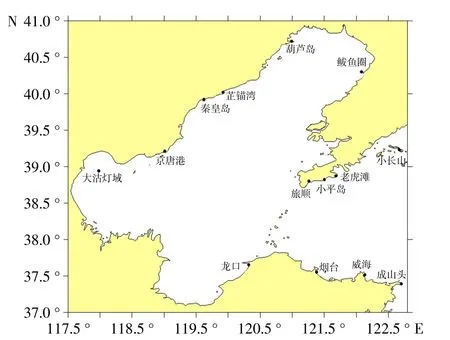
图3 验潮站分布图
为了评估潮汐数值模拟的精度,选用14 个长期验潮站作为验证点(图3),分别收集至少12 个月的实测验潮数据,对验证点进行调和分析。潮汐的调和常数具有稳定性,由潮汐场模型内插出验证点处的调和常数,将内插得到的调和常数与由实测数据得到的调和常数相比较来验证模拟精度。表1为其中4 个验证点处8 个主要分潮的调和常数的对比,其中驻H(cm)表示振幅差,驻g(毅)表示迟角差。
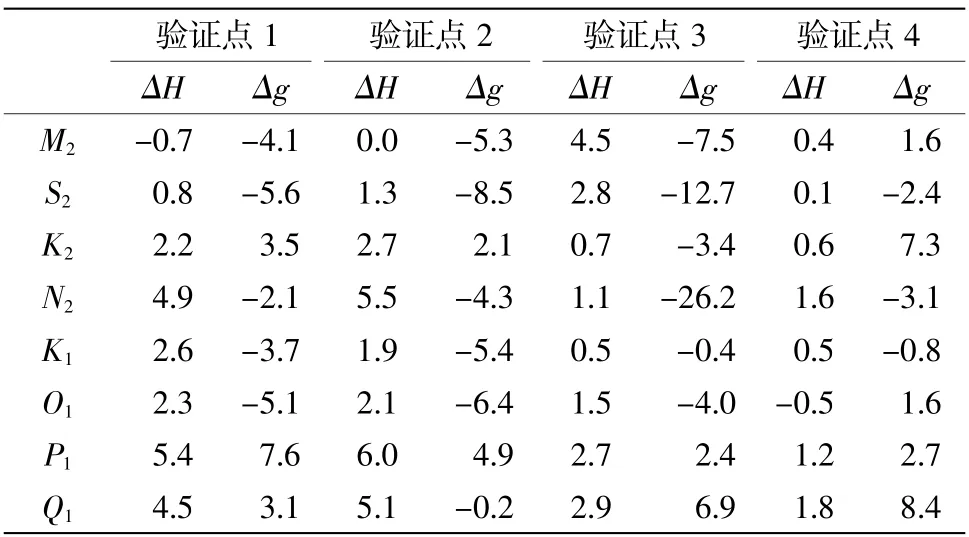
表1 调和常数对比
为直观表征验潮点各分潮的振幅和迟角误差,来检验POM 模拟精度,从图4 和图5 中可以看出,4 个验潮点中除个别几个分潮振幅和迟角误差偏大之外,误差都在允许的范围内。产生误差的可能原因是为了提高计算效率,降低了地形的分辨率,模型分辨率不够,在有些岸线弯曲程度复杂的地方处理不够精细,还有可能就是水深资料不够准确,造成局部误差过大。但总体来讲,调和常数的计算值与实测调和常数值相差较小,模拟精度基本符合要求。通过对验证点的振幅差和迟角差分析,实现渤海M2、S2、K1、O14 个主要分潮的伴随同化数值模拟。所得4 个主要分潮的调和常数精度为:振幅绝均差分别为1.4 cm、1.25 cm、1.37 cm、1.6 cm;迟角绝均差分别为:4.6毅、7.3毅、2.57毅、4.27毅,由于模拟区域受M2和K1分潮影响最强,较前人(高秀敏,2010;朱学明,2009)相比,本文研究的精度均有所提高。
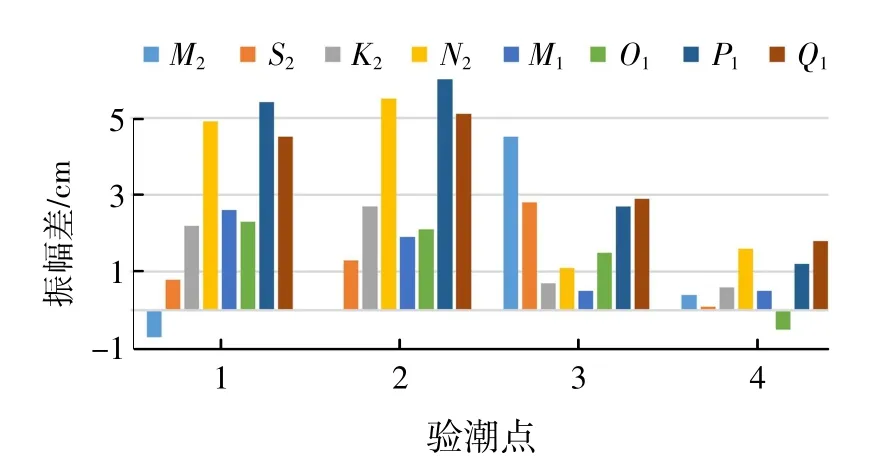
图4 4 个验潮点各分潮振幅误差对比图
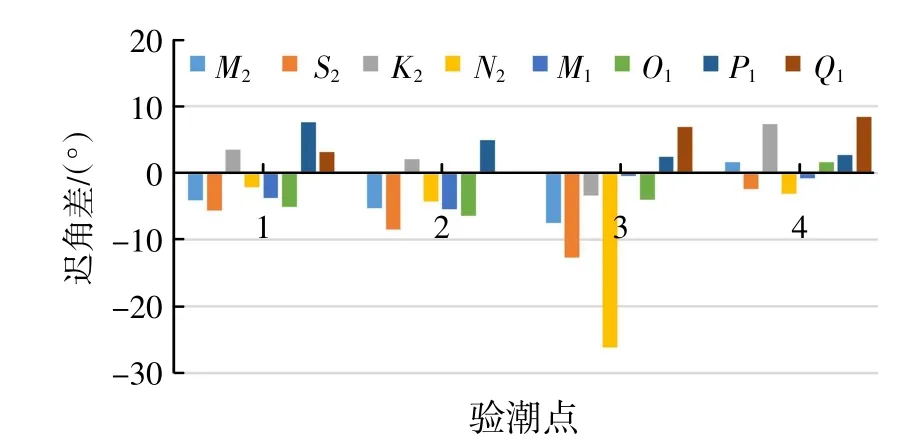
图5 4 个验潮点各分潮迟角误差对比图
对比调和常数,计算结果与实测结果吻合良好,对计算结果进行准调和分析,对M2、K1、O1和S2分潮同潮图进行分析(图6),其中M2、S2半日分潮在计算区域内形成了两个无潮点,其中一个比较明显的点位于秦皇岛外海附近海域,较不明显的一个点位于老黄河口位置,由于填海造陆等人类活动的影响,导致海岸线急剧变化,从而影响了潮流的运动,导致无潮点已退化到陆上,通过与(朱学明,2009;郑鹏,2013)的研究对比可发现,M2和S2分潮的振幅和迟角的走向基本一致,S2分潮的情况与M2分潮类似,在渤海也存在两个无潮点,且两个分潮的最大振幅均出现在辽东湾顶。K1和O1分潮在渤海中各存在一个无潮点,均位于渤海海峡中央附近,振幅最大值均位于辽东湾顶,且迟角线沿逆时针方向旋转,上述结果与前人的研究也是比较一致的。在渤海海区,M2分潮是其主要潮波系统,由M2分潮的模拟结果可见,本模式在渤海海区的本次模拟应用是较为成功的,结果也是合理可信的。
2.5 连续深度基准面的建立
根据模拟得到潮位数据的调和分析结果,建立研究区域连续深度基准面,其具体步骤为: (1)在模拟海域建立1.2忆伊1.2忆的网格,(2)应用数值模型计算各网格点的13 个分潮的值,(3)按照《海道测量规范(GB12327—1998)》1998 规定的13个分潮模型构建整个研究区域的连续深度基准面值,(4)通过网格点的(B,L,H)拟合三维曲面,此曲面即连续深度基准面。由于我国渤海湾近岸海域缺乏长期验潮数据且该区域存在无潮点,潮汐性质复杂。为了与历史上沿用的海图基准面一致,同时又保持基准面分布的平滑性,根据渤海湾西部的天津港原东突堤、大沽灯塔和黄骅港工作码头3 个验潮站处的海图基准面,用下列方法对计算的深度面做了调整。
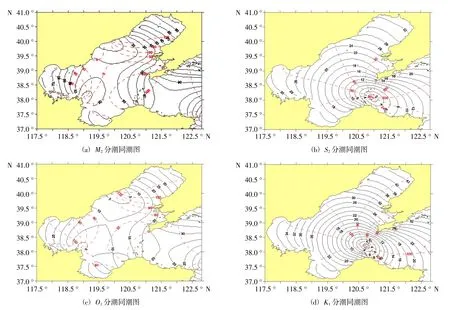
图6 分潮同潮图
(1)采用线性插值方法,将网格点数值插值到所选验潮站处。
(2)计算验潮站处基准面数值与网格点插值结果之比。

其中,Z 表示基准面数值;下标O 和C 分别表示观测值和网格点插值结果,通过此式来帮助建模和验证模拟精准面精度,其值越接近于1,模拟的越精确。
(3)采用距离加权平均的方法,对网格点结果进行调整,权重函数如下:

其中,N 是所选验潮站的个数;d(N)是第N 个验潮站到网格点的距离;a 取0.9 时既可以抚平短期波动,还起到了平滑的作用。
(4)对调整后的结果进行平滑。
渤海湾西部验潮站深度基准面值与模拟数据计算深度基准面值如表2 所示。
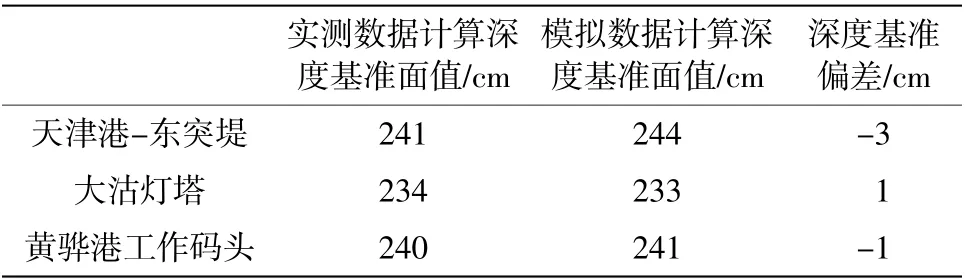
表2 渤海湾西部验潮站深度基准与模拟结果
如表2 所示,各验潮站处的实测数据计算深度基准值与模拟数据计算深度基准面值的偏差很小,3 个站点处的深度基准面差值的绝对值平均为1.67 m,从表中可直观地看出深度基准偏差值最大为-3 cm,在天津港-东突堤站,该站位于港口末端出海口处。显然,这与POM 模式模拟的精度有关。在模型格网覆盖区域的边缘地带,潮位模拟精度和深度基准推算精度一般较差;而在模型内部区域,潮位模拟精度和深度基准推算精度较高。
2.6 CGCS2000 深度基准面模型建立
为实现卫星测高获得的平均海面到海图水深的转换,根据深度基准面模型,结合海底地形,将海图水深的基准面换算为CGCS2000 椭球面。
CGCS2000 参考椭球面与深度基准面之间的关系不能直接求得,需要建立与其他基准面的转换关系模型,找出CGCS2000 参考椭球面与深度基准面之间的关系。通过对海底地形的测量,建立海底地形模型、深度基准面模型和平均海平面模型,可以实现深度基准面到CGCS2000 参考椭球的转换。这几个基准面之间的转换关系如图1 所示。通过计算可得出深度基准面与CGCS2000 参考椭球面的距离AC,用公式可表示为:

式中:PA 表示平均海平面到理论深度基准面的距离,PC 为平均海平面到CGCS2000 参考椭球面的距离。
3 海底地形测量与通航水深应用模式
3.1 基于精密定位定姿系统(position and orientation system)的海底地形测量
在统一的参考椭球和深度基准面等海洋垂直基准基础上,可以采用精密POS 及测深仪进行精密的海底地形测量。在CGCS2000 地心坐标系中,陆地表面和海底表面的每一个点都有明确的坐标,并且在一定时段内保持稳定。同时,通过精密POS进行三维测量,能够获取符合海道测量精度要求的卫星天线高(基于椭球面的大地高),经过精密计算,能够得到与卫星天线高的精度相当的海底大地高。基于精密POS 的海底地形测量时卫星接收机天线架设及高程计算原理如图7 所示。
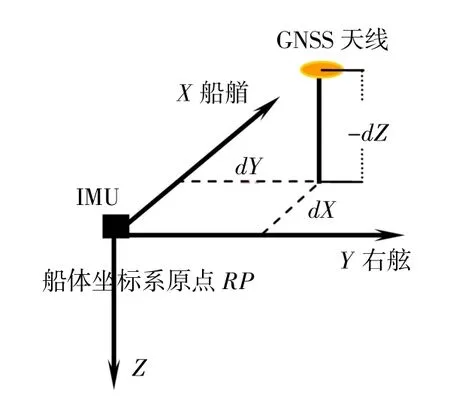
图7 GNSS 高程计算原理图
由GNSS 和测深设备直接测量海底点的大地高的公式为:

式中:HGNSS为GNSS 天线处的大地高;z 为GNSS 天线到重心位置RP (Reference Point)的垂直距离;h 为换能器表面至RP 的垂直距离;D 是测深仪测量的换能器表面至海底的垂直距离。至此,通过姿态变换,实现了定位、测深的一体化改正,完成了精密水下地形测量。
3.2 通航水深的应用
装备了高精度GNSS 的船舶进行航行时,可实时进行船舶的大地高测定,并通过已知海底的地形模型计算实时水深:

式中:HGNSS是GNSS 的天线高,H海底是船舶所在位置的海底高,HW是船舶吃水线到GNSS 天线的垂直距离,可由GNSS 天线的安装高度和船舶吃水计算得到。相较于传统的水深测量方法,采用精密POS测量和通航水深应用模式跳过了复杂的潮汐变化对水深测量精度的影响,可以直接获取海底的大地高。对于过于保守的深度基准面值虽然可以保障船舶的航行安全,但造成了航道水深利用率和航道维护费用增加等问题,通过航行船舶自身的高精度GNSS,可获取瞬时海面到海底的深度,能够解决船舶在港口水域水深利用率低和港口航道维护费用高的问题。实时水深测量应用模式如图8 所示。
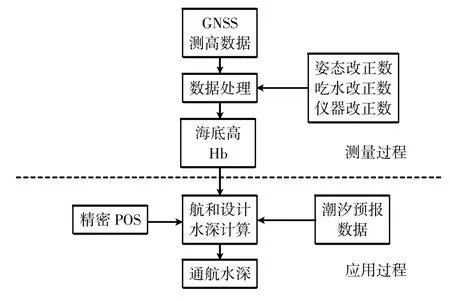
图8 即时水深测量应用模式图
3.3 基于e-航海的通航水深智能服务
由高精度GNSS 测量和应用模式获得的通航水深数据和数据库数据,可通过AIS 和Internet 等实时数据传输方式发布给用户,实现一种自主、高效、可靠、经济的个性化智能服务模式,为用户提供水深浅点预警信息、潮汐信息、电子海图更新等推送服务。信息推送技术有助于很好的保证数据传输的实时性,符合e-航海战略的宗旨。在航行前,船舶将自己的航行计划上传至岸端服务器,利用高精度通航水深应用模式,由岸端服务器计算出该航行区域的实时水深图。e-航海服务端还可为用户智能推送最佳航线和通航时段,其具体服务模式流程如图9 所示。
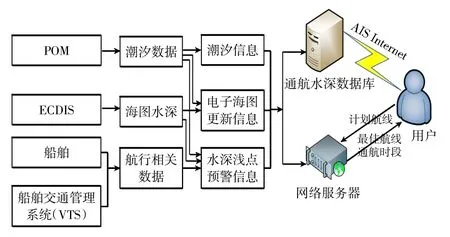
图9 通航水深智能服务流程图
4 结论
本文对基于高精度GNSS 的通航水深服务模式进行了探讨,采用计算精密海面数值模型获取的海面高与海底大地高之差的方法获得水深值。研究结论如下:
(1)采用POM 模式对渤海湾西部海域进行了潮波运动模拟,模拟所得网格点潮汐特征符合当地实际潮汐特征,并在此基础上构建高精度的连续深度基准面,根据模型计算结果分析可知,模型整体精度较高。
(2)通过卫星测高的方法获得平均海面,由平均海面、深度基准面和海底建立转换模型,将深度基准面归算到CGCS2000 参考椭球面。
(3)基于精密POS 测量技术直接进行海底地形测量,建立与陆地地形相衔接的数字地形模型,并可应用于船舶获取动态水深。
(4)e-航海服务体系能够为船舶提供智能化通航水深服务。
本文提出的通航水深服务模式应用精密POS测量技术进行高精度海底地形测量,建立与陆地地形相衔接的数字地形模型,另一方面,建立与时间及空间位置相关的潮汐变化模型,在船舶航行时,能够实时解算船舶所在位置或未来某一时刻船舶航行至某位置的水深值,由此可指导船舶在水深比较接近船舶吃水区域的航线、航行时间的选择。除此之外,该服务模式在港口建设和海洋科学研究中也将发挥重要的作用。
致谢:天津航海仪器研究所张永兵为文章修改提出宝贵意见,在此一并致谢。



