基于MODWT 变换的海洋重力观测航行数据滤波方法
2020-12-11孙鹤泉金绍华张宇
孙鹤泉,金绍华,张宇
(海军大连舰艇学院 军事海洋与测绘系,辽宁 大连 116018)
海洋测量船搭载海洋重力仪实施重力测量时,重力仪在受地球自转产生的离心力影响的同时,还受到测量船移动产生的附加离心力的影响,出现厄特弗斯效应,产生额外的扰动加速度,扰动加速度与重力加速度相混叠,影响海洋重力测量的精度。在海洋重力测量中,厄特弗斯效应是主要误差源,是所有修正项中最大的影响项,海洋重力测量数据需要经过多项修正,才能得到重力空间异常、布格异常成果。厄特弗斯效应无法通过改进仪器和增加附属设备来消除,只能通过相应的数据处理进行修正(韩孝辉等,2017)。
对海洋重力测量数据进行厄特弗斯改正时要用到测量船航速和航向角的数据,海洋调查规范要求测量船在海洋重力测量过程中沿着设计测线匀速直线航行,航速和航向角误差要在规定的范围内(国家海洋局,2007)。受海况及环境因素影响,差分GPS 得到的航速和航向角时间序列存在较大误差,需要对航速和航向角数据进行滤波处理来削弱这些误差的影响,提高航速和航向角的测量精度,满足海洋调查规范要求(张会等,2011)。
噪声干扰无处不在,从含噪信号中滤除干扰,提高信噪比具有实际应用价值。根据噪声能量集中在高频,有效信号的能量分布在低频这一特点,研究人员提出了多种降噪滤波方法,面对众多的滤波方法,需要对滤波器类型与参数进行合理选择。多数常规滤波器是前验性的,即对信号和噪声的分布类型进行特定假设,利用信号中噪声的一些特征或统计参数才能很好地实现滤波,降低了滤波器对信号与噪声的自适应功能。在缺乏先验知识的情况下,采用小波变换进行降噪处理成为研究人员的一种很好选择。在采用定量化的Lipschitz 条件来确定小波收缩阈值的基础上,本文提出了一种利用具有平移不变性的最大重叠离散小波变换(Maximal Overlap Discrete Wavelet Transform,MODWT)进行海洋重力观测中航速和航向角数据滤波的算法,并通过分析实测数据验证了算法的可靠性。
1 理论基础
只考虑加性噪声,可以将观测信号X(t)分解为如公式(1)所示的两部分:
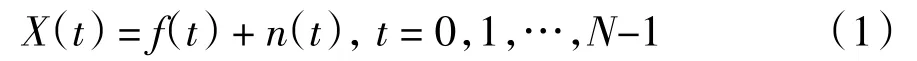
其中,f(t)表示信号中的有效部分;n(t)表示信号中的高斯噪声或高频波动;本文算法主要用来消除或抑制公式(1)中的第二项n(t)。
1.1 MODWT 变换
MODWT 变换是小波分析领域中较新的一种形式,也是离散正交小波变换的一种变形拓展。与正交小波变换相比,MODWT 变换是一种高冗余度非正交变换,但具有平移不变性,可以弥补正交小波变换的固有缺陷。与正交小波一样,MODWT 变换也可以通过塔形算法进行高效计算,只需将正交小波变换在滤波器设计上做些细微的修改即可实现MODWT 变换,且计算复杂性与FFT 算法相同(Donald et al,2000)。本文采用MODWT 变换是因为其具备如下特点:
(1)J 级的正交小波变换要求信号序列的长度为2J的整数倍,而MODWT 变换对信号序列的长度没有要求;
(2) 通过MODWT 变换实现信号的多分辨率分析,变换的细节部分和光滑部分是与零相位滤波器相关的,可以提取出原信号中的关键特征;
(3) 信号序列的循环平移的MODWT 变换与信号序列的MODWT 变换的循环平移相对应;
(4) 可利用MODWT 变换的小波系数和尺度系数进行信号的方差分析。
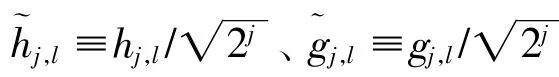
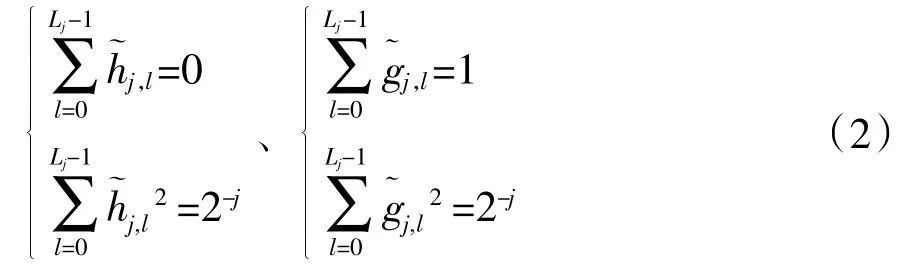
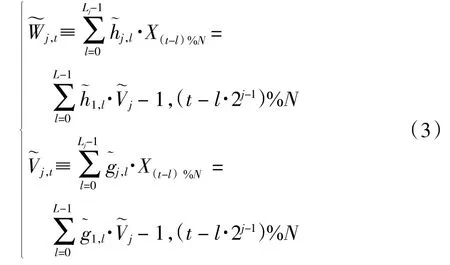
其中,t=0,1,…,N-1。
1.2 高斯噪声

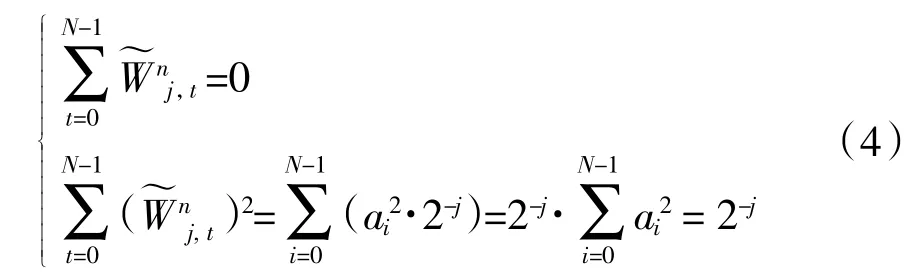

1.3 收缩阈值
与正交小波变换一样,公式(1)中信号X(t)的特征可以用其MODWT 变换的小波系数来描述:较大的系数对应较多的信息、较小的系数对应较少的信息。根据数值大小来衡量小波系数在信号中所占比重,利用MODWT 小波进行信号降噪就是对绝对值较小的小波系数进行阈值收缩处理(Donald et al,2000),把低于阈值的小波系数作为噪声进行置零或收缩处理。
在对MODWT 小波系数进行阈值收缩处理过程中,阈值的选取直接影响到小波降噪的处理效果。阈值选择过大,会导致过滤波,信号过度光滑,丢失边缘等局部特征;阈值选择过小,则造成欠滤波,噪声抑制不够,达不到降噪目的。为了避免过滤波和欠滤波的出现,本文以假设观测信号光滑连续为前提,利用表征函数正则性的Lipschitz条件来确定合适的收缩阈值。
如果函数f(x)满足Lipschitz 条件,那么存在常数L,对定义域内任意两个自变量,有公式(6)成立。
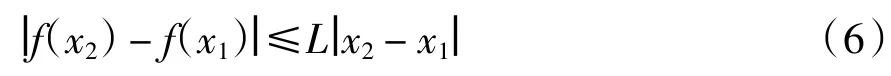
公式(6)是定性描述表征函数正则性的Lipschitz 条件,所有文献中关于常数L 的计算方法并无太多介绍。为了能够定量使用Lipschitz 条件,本文对公式(6)进行了改进。利用Donoho 等(1995a,1995b) 提出的MAD 中位数阈值估算方法获得初始阈值(Donald et al,2000),依次小幅增大阈值,直到重构信号满足公式(7)所示的条件为止,实现信号重构。
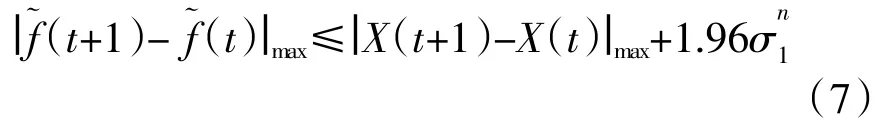
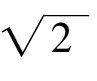
2 算法测试
为了验证上述算法的降噪性能,模拟生成如图1 所示的理想信号和随机加噪信号。

图1 理想模拟信号与随机加噪信号
利用传统频域低通滤波方法对图1(b)中的加噪信号进行光滑处理,得到如图2(a)所示结果,图2(b)则为利用本文算法分析得到的结果。
对比图2 中的两组分析结果可以看出,本文算法在消除噪声的同时,很好地保留了信号的局部特征;进一步计算两种方法的信噪比,分别为29.82、33.32,也能够体现出本文算法的优势。

图2 降噪处理后的信号
3 数据分析
下面提供了两组实测信号及处理结果,用来验证本文方法的可靠性和实用性。图3 和图5 中列出了在中国南海某区域进行重力测量时的航速和航向角数据,从图中的曲线可以看出,原始观测数据中存在明显的噪声干扰。考虑到小波的光滑性、消失矩和紧支区间等因素,本文选用db-3 小波作为基函数,图4 和图6 中列出了采用本文方法处理后的滤波结果。
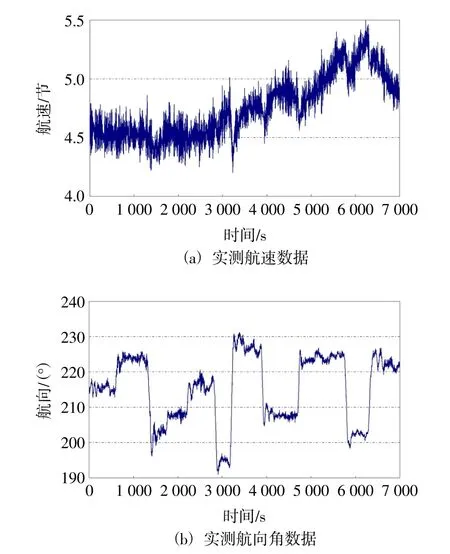
图3 第一组实测航行数据曲线

图4 降噪滤波后的第一组航行数据曲线
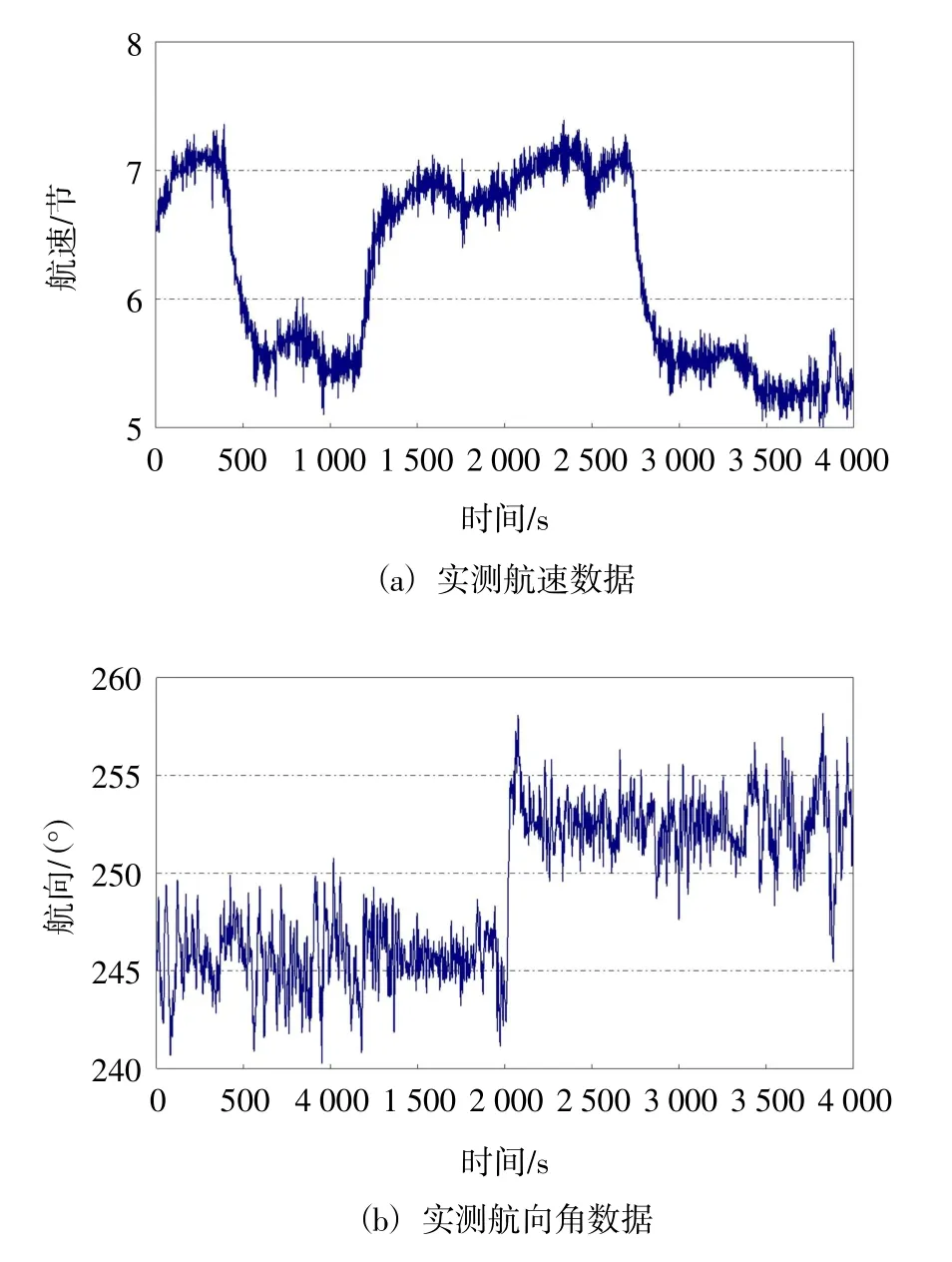
图5 第二组实测航行数据曲线
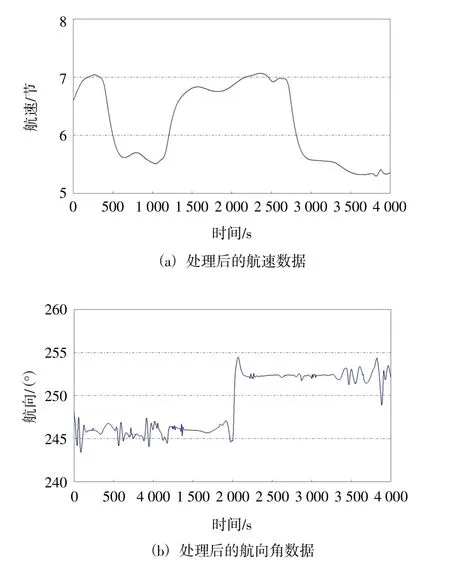
图6 降噪滤波后的第二组航行数据曲线
图3 中相邻测点的角度差最大为3.43毅、速度差最大达到0.42 节,图5 中相邻测点的角度差最大为4.03毅、速度差最大达到0.4 节,且为高频波动,显然是因为波浪等海况因素导入的噪声干扰,航速和航向角误差已经超出规范规定的范围(国家海洋局,2007)。图4 中相邻测点的角度差最大为0.99毅、速度差最大达到0.004 节,图6 中相邻测点的角度差最大为0.74毅、速度差最大达到0.021 节,很好地抑制了信号中的噪声成分,符合规范要求。同时本文方法准确地保留了信号的局部特征,便于后期对数据进行分段处理。
4 结论
海洋调查数据中的噪声干扰对数据后期分析和参数计算的影响很大,削弱噪声干扰能够显著提高数据信噪比,突出观测数据中的关键特征。本文利用MODWT 变换和改进的定量化Lipschitz 条件,从高斯噪声小波系数的分布特性入手,提出了一种海洋重力观测中含噪航行数据的滤波方法。本文方法能够准确重构观测数据中的有效信号,在去除噪声干扰的同时,又不致重构信号失真。对比本文提供的模拟信号和两组实测数据及滤波处理结果,可以验证本文方法的可靠性与有效性。

