1979—2018 年长江口及邻近海域风速和波高的分布特征与变化趋势
2020-12-11吴秋原史本伟黄远光杨世伦
吴秋原,史本伟,黄远光,杨世伦,2
(1.华东师范大学河口海岸学国家重点实验室,上海 200062;2.崇明生态研究院,上海 200062)
气候变化是海洋与大气科学研究的重点之一,风速的变化以及由海上风场引起的海面波动是气候变化研究的重要内涵。海表面风速以及包括有效波高等在内的各种海浪要素,都对海-气相互作用的过程具有重要的影响,与发生在海-气界面和海洋上混合层的能量交换存在密切的关系(Young et al,2011)。以往对风速、波高的观测手段,如气象站、船只定点或走航观测只能提供极其有限的数据,且观测成本高,限制了人类对海洋的认识。卫星遥感技术的出现有效地解决了这个问题,例如通过主动式微波测量的雷达高度计(Chelton et al,2001),能够在全球范围内全天候、重复测量瞬时海面高度、波高和风速。而随着计算机技术的发展,数值模拟的方法也越来越得到广泛的应用。另外,通过卫星数据与数值模拟同化并结合实测资料校准,可以得到更合适的数据资料进行研究。如Zieger 等(2009)对1985—2008 年全球卫星观测资料进行系统的校准与同化,提供了长时间连续的数据集。
全球气候变化背景下河口海岸地区风浪的趋势变化是一个具有重要应用背景的科学问题。已有的风浪变化研究一部分着眼于全球的分布变化,如Sergey 等(2004)利用国际综合海洋大气数据研究发现过去百年北太平洋风浪波高呈显著的正趋势,Young 等(2011)利用卫星同化资料分析全球风速与波高的长期变化趋势。一部分着眼于中国近海局地变化,如李荣波等(2016)基于ERA-40 资料计算1957—2002 年南海海表风速、波高的分布特征与变化趋势。长江口地处东海之滨,受季风和台风影响,波浪作用强烈(肖文军,2008)。学者对其所在东海海域进行了相关研究,如刘志宏等(2011)利用CCMP 资料对西北太平洋1988—2009年海表风场进行研究,发现西北太平洋大部分海域风速呈显著递增趋势。作为河口海岸水域重要动力条件之一,风浪变化不仅会影响流场、泥沙运动、水体浊度、底床稳定性等自然过程(哈长伟等,2009;肖林等,2018),也会影响通航条件和海岸防护工程的安全,故研究长江口海域风浪要素的分布特征与变化趋势具有重要的意义与价值。
对于该区域而言,由于过去观测资料的限制,以往研究中较少同时对较长时间序列与较大空间系列的数据资料进行分析,且很少结合风、浪要素研究其特征与关系,本文的创新之处是基于欧洲中期天气预报中心最新的ERA5 与ERA-Interim 再分析资料进行系统化、网格化的分析,统计分析近40 年(1979—2018 年) 长江口及其邻近海域风、浪要素的季节特征,利用EOF 分解法分析风、浪场的空间分布特征及其关系,Mann-Kendall 检验法分析该海域风浪要素年际变化趋势,并结合全球变暖背景下海平面的变化,分析该海域波高在未来可能的变化趋势。
1 资料与方法
1.1 数据资料
本文使用欧洲中期天气预报中心(ECMWF)ERA5 与ERA-Interim 再分析资料,其基于欧洲中心IFS version Cy31r2 系统模拟得到,并使用4DVar 分析方法同化大量卫星高度计、浮标等观测数据以及海浪模式数据(王传辉等,2018;庄晓霄等,2014)。ERA-Interim 全球海洋与大气再分析资料是继其早期ERA-15 和ERA-40 后的产品,ERA5 则是EAR-Interim 后优化推出的新产品。Dee 等(2011) 验证了ERA-Interim 数据的优越性,指出其在很多方面都超出预期值。前人据此资料进行过不少相关研究,如Semedo 等(2001)通过ERA-40 研究分析了1957—2002 年全球风浪和涌浪的气候态特征,庄晓霄等(2014)通过ERAInterim 对全球海表风场与波高等进行统计分析,并揭示了风浪与涌浪的分布特征。在中国近海该资料亦有相关应用经验,如Wu 等(2014) 利用ERA-Interim 与ERA-40 波浪数据结合20CR 再分析资料构建1911—2010 年中国海域波高Hs-SLP多元回归模型,分析发现波高在南海中部春夏季以及东海夏季存在显著递增趋势,李荣波等(2016)通过ERA-40 资料计算了1957—2002 年南海海表风速、波高的分布特征与变化趋势。总结前人的应用经验,本文选取的数据资料具有相当的可靠性。
1.2 分析方法
本文选择的研究区域为29毅—33 毅N,120毅—123 毅E,包括长江口、杭州湾在内的东海西北部海域,如图1。针对该研究区域,提取1979—2018年ERA5 月均海表面10 m 风场(以下简称风场、风速、风向),和ERA-Interim 每日8 时次风场、每日4 时次混合浪海浪场,包括有效波高(swh,以下简称波高)、平均波周期(mwp,以下简称波周期)、平均波向(mwd,以下简称波向)。本文使用EOF 经验正交函数分解法分析1979—2018 年长江口及邻近海域风、浪场的空间分布特征,使用Mann-Kendall(M-K)检验法分析该段时间内风速与波高的变化趋势。
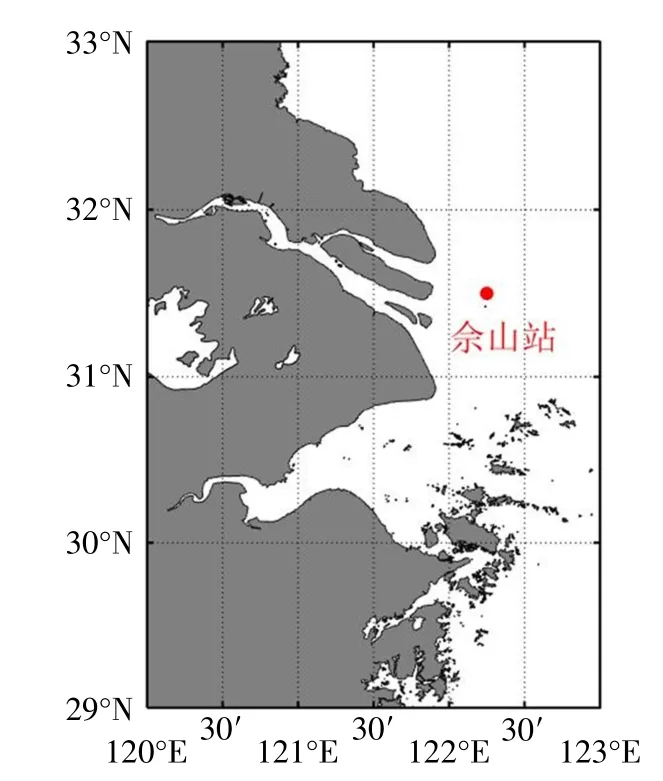
图1 长江口及其邻近海域(研究区域)
1.2.1 EOF 分析
EOF(Empirical Orthogonal Function)是一种分析矩阵数据中结构特征、提取主要数据特征量的方法,最早由统计学家Pearson(1901)提出,后来被引入气候研究领域。分析过程中特征向量对应空间样本的称为空间模态,对应时间变化的称为时间系数。基本思想是将观测场序列分解成相互正交的时间函数与空间函数的乘积之和。将空间函数看作典型场,时间函数看作典型场的权重系数,则不同时间的要素场是若干个要素场按不同权重线性叠加的结果。海洋资料中过程与关系错综复杂,为了简化分析又尽量少损失信息,需提取多变量之间的主要特征变量,利用其相互关系构造独立的新变量,从而达到降维分析。本文使用EOF 分解对研究海域内1979—2018 年间的风、浪场进行展开,滤去随机干扰,保留统计上最显著的两个典型模态,探讨研究海域内风、浪场的空间分布特征及其关系。
1.2.2 M-K 趋势检验法
M-K(Mann-Kendall)检验法是一种针对随机分布的非参数检验法,被广泛运用于水文资料分析,能够检验线性或者非线性趋势(Mann,1945;Kendall, 1948)。零假设(H0) 表明数据序列(本文中为风速和波高数据序列)是独立恒等分布的随机样本,即在此前提下风速与波高不存在趋势变化。
在M-K 检验法中,定义检验统计量S 为:
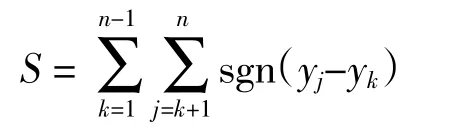
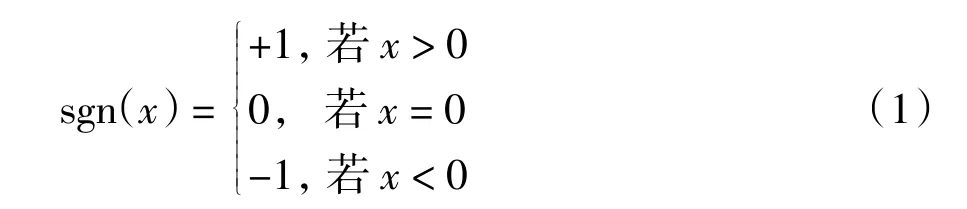
在零假设(H0)的前提下,随着数据序列长度趋向无穷(即风浪要素资料数据无限长),统计检验量S 呈对称正态分布,均值为0,方差表示为:

其中,n 为数据序列长度。时间双边的趋势检验通过对以下统计量的比较实现:

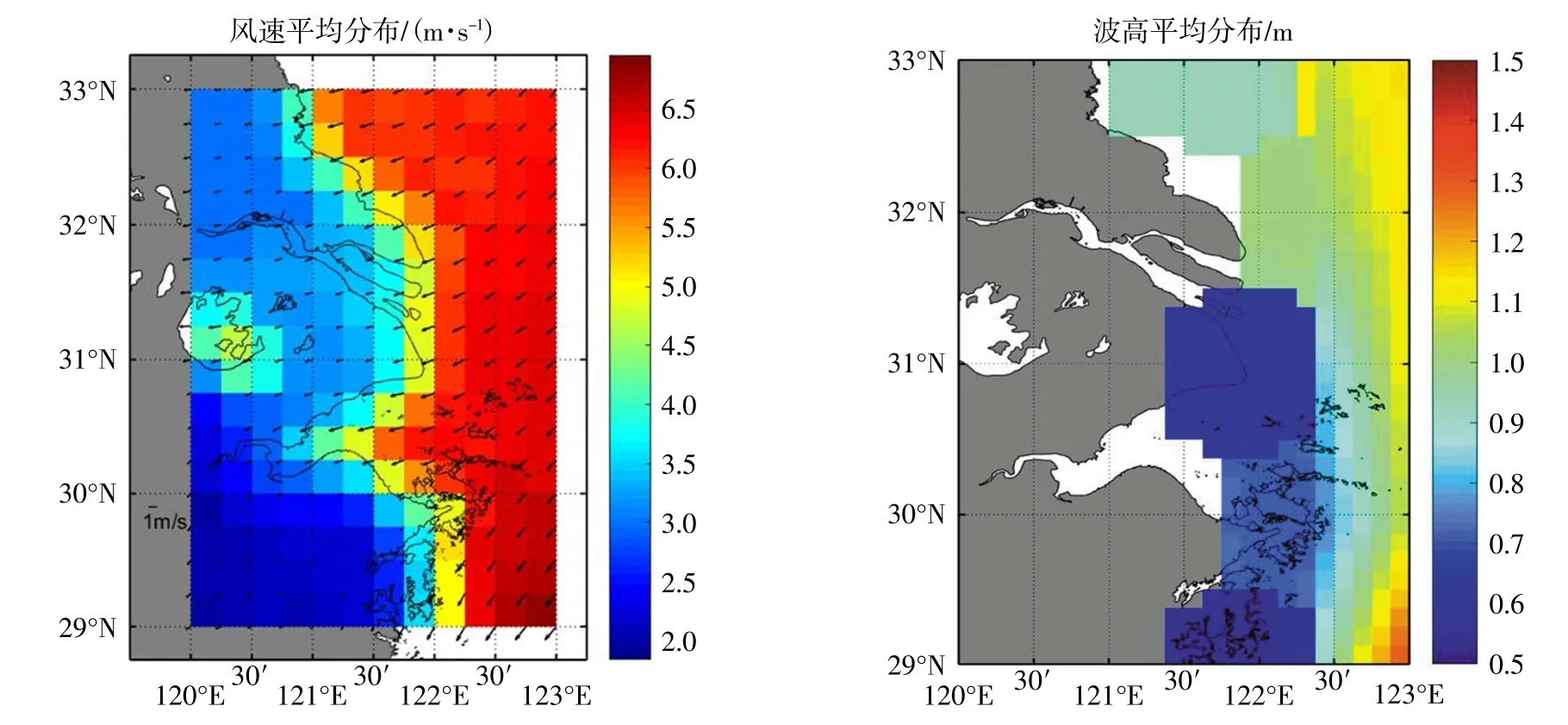
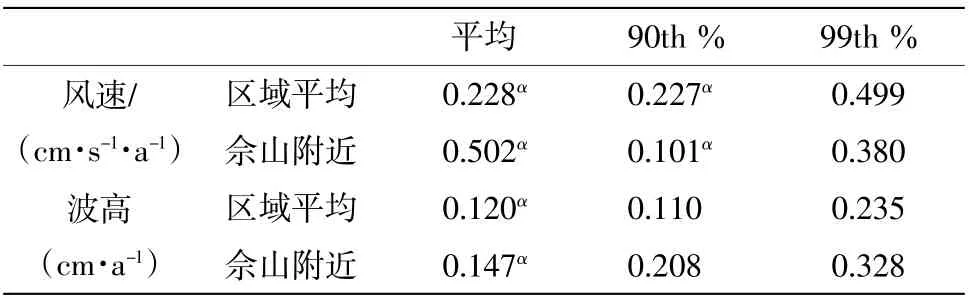
若渣Z渣 当趋势显著存在时,用ti表示第i 次观测的时间长度,则对于1 其中值表示无偏估计下趋势变化的斜率,本文据此定义风浪要素的年际变化速率。 对ERA5 与ERA-Interim 资料场统计得1979—2018 年研究海域内风、浪场要素的变化范围与均值如表1 所示,表明当发生极端气候事件时,相关要素数值会远超通常的波动范围。图2 是研究海域风速风向与波高40 年平均分布。其中阴影部分表示风速或波高大小,箭头长度表示该处风速,箭头方向表示该处风向。可见近岸海区风速与波高整体小于外海,且越趋向外海,风速与波高越大。其原因主要是由于海陆热量分布存在差异,以及陆地摩擦相对较大。而波高的分布受风速影响,又由于近岸地形引发能量耗散,故波高减小。 图2 1979—2018 年平均风场与波高的分布 使用EOF 经验正交函数分析方法对研究区域1979—2018 年风、浪场提取典型模态场,并探讨空间分布特征及其关系。对风、浪要素数据各自计算月平均距平场作为EOF 分析的原始资料矩阵。表1 为风速与波高前3 个主要模态的方差贡献率,第一模态方差贡献率分别为72.5 %和93.95 %,前两个模态累积方差贡献率各自达87.79 %和98.11%,故取前两个模态分析能充分反映风浪要素逐月变化的主要空间分布特征。 图3 风速前两个模态空间分布 表1 风、浪要素统计值 表2 年际变化风速与波高前三个主要模态的方差贡献率 图3 为风速前两个模态空间分布。可见风速第一模态总体呈正偏差值,并沿长江口内至近岸再向外海越来越高,其风速变化梯度逐渐增大。第二模态方差贡献率15.29 %,零偏差值大约沿着NESW 走向分布至舟山群岛附近,其以东南分布呈负值。图4 为波高前两个模态空间分布,第一模态总体呈正偏差值,且由长江口近岸向外海正偏差值逐渐增强。第二模态方差贡献率约4.16 %。对比风速与波高第一模态分布形式,其梯度方向近似,两者间存在密切对应关系。但第二模态的分布形式有明显的差别,说明海浪场分布并非完全由风场决定,而波浪的浅水效应以及涌浪分布等可能是造成两者空间分布差异的原因。 图4 波高前两个模态空间分布 长江口属亚热带季风气候区,其所在东海海域受盛行东亚季风影响。夏秋季盛行东南风,暖流系统加强,沿岸流系统变弱,通常海况下波浪作用较弱,而夏秋季大浪以台风浪为主,作用时间较短,对均值影响不大,但台风过境时风大浪高,出现一年中的风浪要素极端值。冬春季盛行西北风,沿岸流系统增强,暖流系统减弱并向南退缩,大浪以寒潮浪、气旋浪为主,作用时间较长,波浪能量较强,故均值通常较高。针对长江口风、浪要素季节特征分析,本文记3 月至5 月为春季,6 月至8月为夏季,9 月至11 月为秋季,12 月与1、2 月为冬季。 图5 为研究海域1979—2018 年风速季节平均分布图,可见外海风速普遍大于沿岸,秋冬季风速普遍高于春夏季,例如在长江口外佘山岛附近春夏季平均风速分别为6.228 m/s 和6.138 m/s,秋冬季则分别为6.380 m/s 和6.582 m/s。图6 为风向季节平均分布,春季风向主要分布在N-E-S,频率合计77.09%,常风向为SSE 向,频率占比10.91%,夏季主要分布在ENE-SSW,频率合计74.82 %,常风向为S 向,频率占比16.49%。秋季主要分布在NNW-ENE,合计62.64%,常风向为NNE 向,频率占比16.79%。冬季主要分布在NW-NE,合计67.4%,常风向为N 向,频率占比19.79%。图7为1979—2018 年波高季节平均分布,可见外海波高普遍高于近岸,秋冬季波高普遍高于春夏季,例如口外佘山岛附近春夏季波高分别为0.572 m 和0.537 m,秋冬季则为0.662 m 和0.695 m。图8 为波向季节分布,春季波向主要分布在N-SSE,频率合计85.39 %,常浪向为NNE 向,频率占比13.29%,夏季主要分布在E-S,合计76.76%,常浪向为SSE 向,频率占比19.25%,秋季主要分布在N-E,合计76.61%,常浪向为NE 向,频率占比19.74%,冬季主要分布在NNW-NE,合计73.18%,常浪向为N 向,频率占比24.30%。对比图6,可见波向与风向的季节分布有一定相似性,这是由于当地风向是影响波浪传播方向的重要因素之一。综上所述,风向与波向的季节统计结果符合长江口所在东海海域受盛行东亚季风影响的特征。 图5 风速季节平均分布 图6 风向季节平均分布 图7 波高季节平均分布 图8 波向季节平均分布 本文通过M-K 检验法对1979—2018 年ERA5与ERA-Interim 风速、波高逐月序列(风速逐月平均序列采用ERA5,其余均用ERA-Interim)进行趋势分析并计算年均变化速率,对研究区域(29毅—33毅N,120毅—123毅E)内计算区域平均,另外选择佘山水文站位置计算结果说明长江口风、浪要素年际变化速率。结果如表3 所示,分别为风速与波高的月平均序列与极端值(90th%、99th%)的年均变化速率。表格注明结果通过显著性水平为5%的检验。结果表明在1979—2018 年研究区域内风速存在0.228 cm/(s·a)的平均递增趋势,累计增长1.6%(相较于均值),佘山站位置风速呈0.502 cm/(s·a)递增趋势,累计增长3.5 %。波高存在0.120 cm/a 的平均递增趋势,累计增长5.4%,佘山站波高呈0.148 cm/a 递增趋势,累计增长9.6%。以百分位数表示的极端值序列中,仅风速90th %年际变化在绝大部分区域通过5 %的显著性检验,存在0.227 cm/(s·a)的递增趋势,佘山站位置为0.101 cm/(s·a)。 表3 风速与波高的年际变化趋势(琢表示数据通过5%的显著性检验) 风速与波高的递增趋势现象与前人的一些相关研究结果一致。如Young 等(2011) 利用卫星同化资料研究发现风速在全球诸多海域存在增高趋势,且极端风速更为明显,极端波高值在中高纬度存在递增趋势。刘志宏等(2011) 利用CCMP 风场资料研究发现1988—2009 年间西北太平洋大部分海域风速呈显著逐年递增趋势。关于波高的变化因素较为复杂,匡翠萍等(2016)利用MIKE21 SW构建长江口波浪数学模型,发现周期性变化中波高总体随海平面上升而增大。根据IPCC 第五次科学评估报告(IPCC,2013)结果表明全球海平面上升的线性趋势在1902—1990 年期间是1.6[1.2 耀2.2] mm/a, 1993—2012 年为3.3 [2.8 耀3.6] mm/a。在全球变暖背景下,长江口及邻近海域波高很可能会随海平面上升而继续增大。而长江口海域水动力环境十分复杂,波要素的变化存在诸多可能的影响因素,因此对影响波高变化的具体因素还需进行更精确的界定。 (1)研究区域内风、浪要素分布整体符合亚热带季风气候特征,波向的季节分布与风向具有一定相似性,表明风向是影响波浪传播方向的重要因素。统计得1979—2018 年间风速变化范围为0耀29.652 m/s,均值为5.762 m/s,波高变化范围为0.062 耀9.670 m,均值为0.896 m,波周期变化范围为1.975 耀13.041 s,均值为4.900 s。当发生极端气候事件时,风浪要素的数值远超通常的波动范围。 (2)风速场空间分布呈W-E 走向递增,外海风速明显高于近岸。波高第一模态在研究区域内均呈正偏差值,其空间分布沿W-E 走向增强,分布形式与风速存在对应关系。第二模态方差贡献率分别为15.29%和4.16%,其分布差别表明波高分布不仅与风速场有关,涌浪场分布可能是影响波高分布的因素之一。 (3) 1979—2018 年间研究区域内风速年平均值总体呈增长趋势,计算得区域平均增长速率为0.228 cm/(s·a),累计增长1.6%,佘山站位置增长速率为0.502 cm/(s·a),累计增长3.5%。波高普遍呈增长趋势,区域平均增长速率为0.120 cm/a,累计5.4 %,佘山站位置增速为0.147 cm/a,累计9.6 %。年际90th%值与99th%值波高与风速则呈不同程度的增长趋势。
2 风速与波高的分布特征
2.1 空间分布
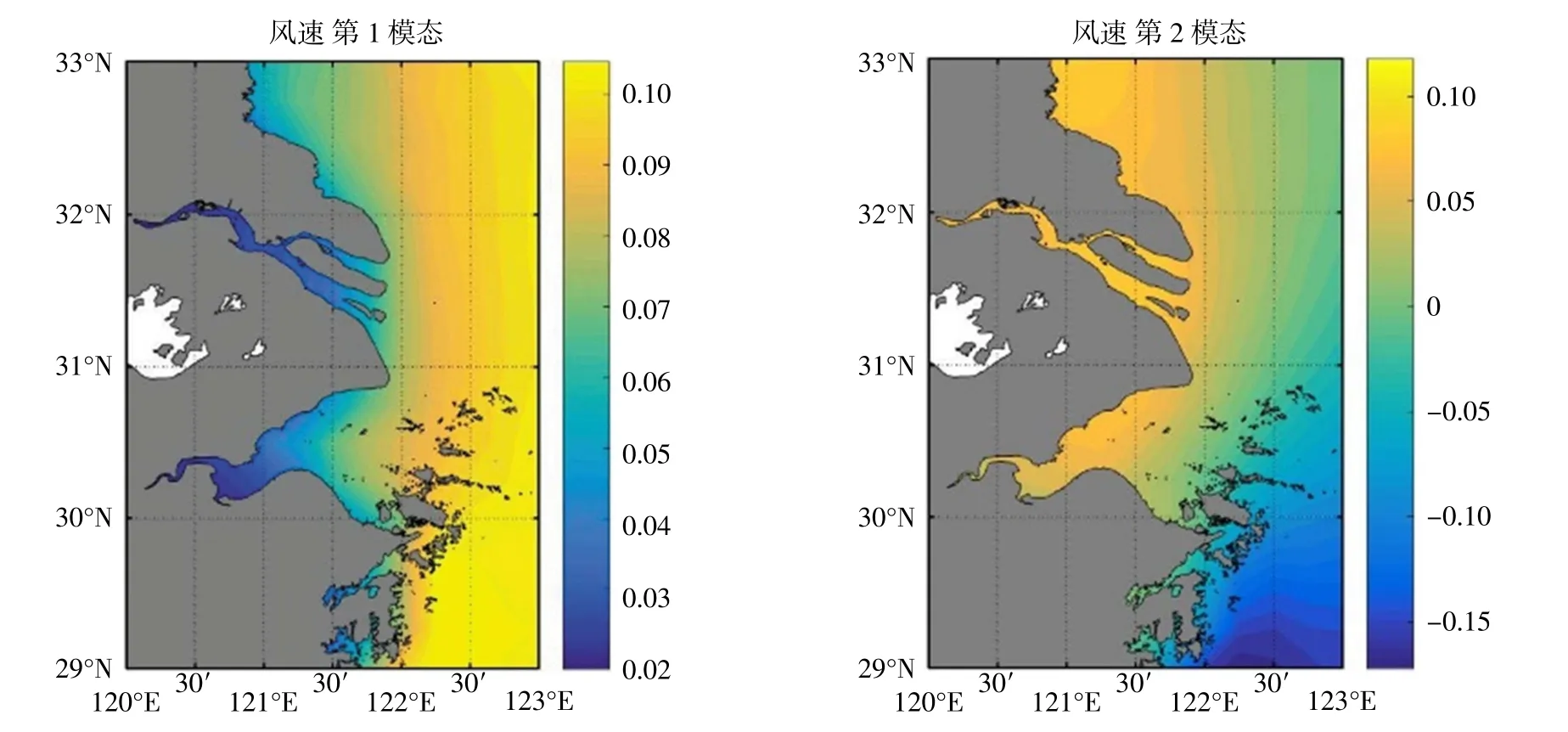
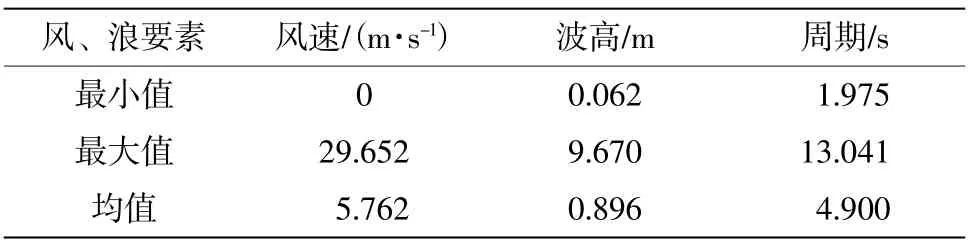
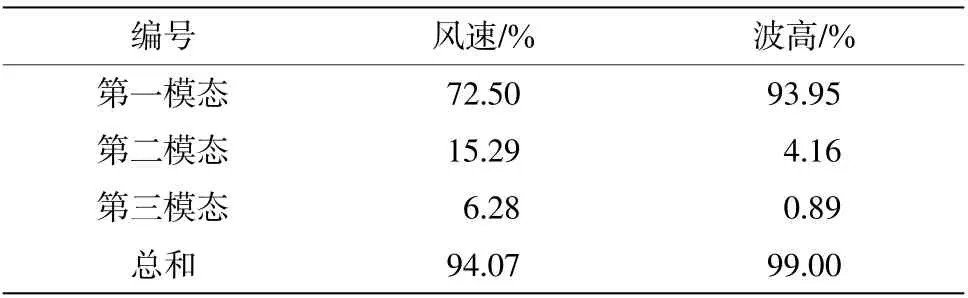
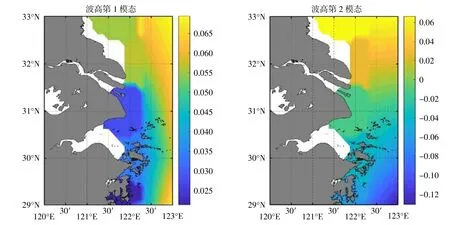
2.2 季节特征
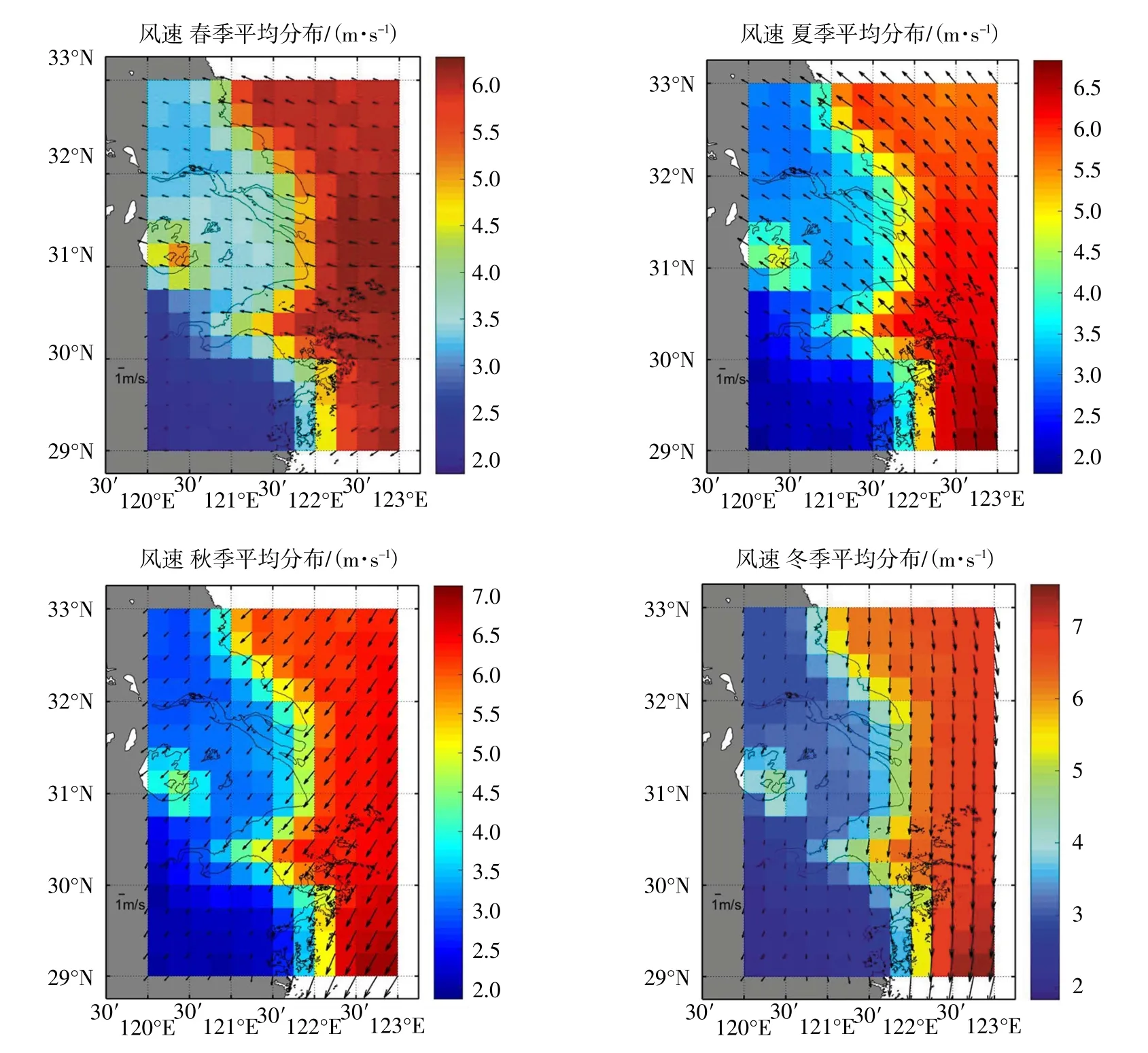
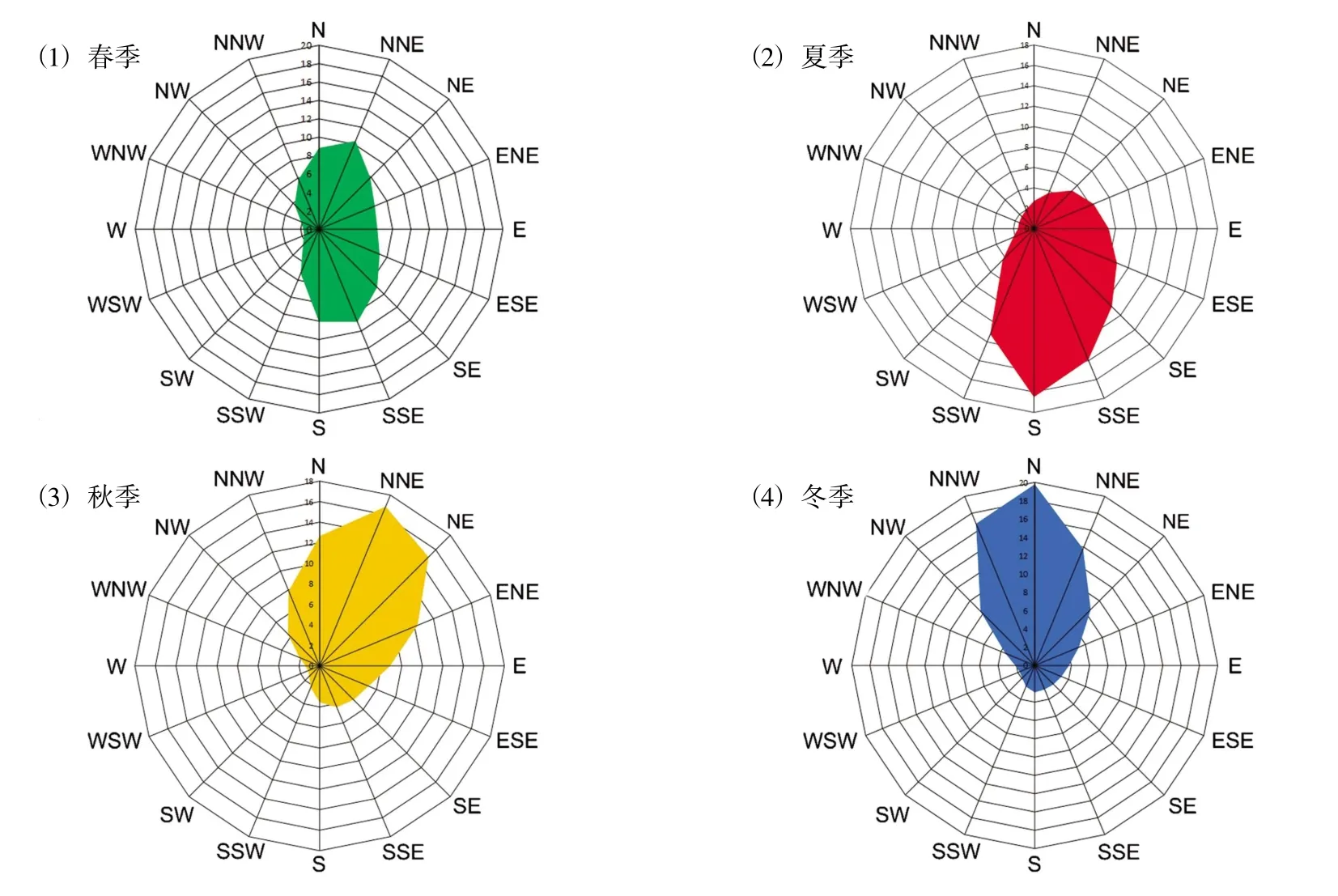
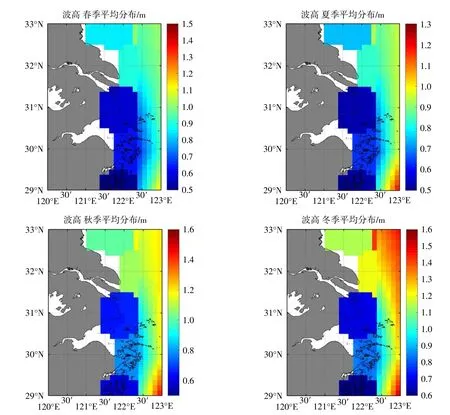
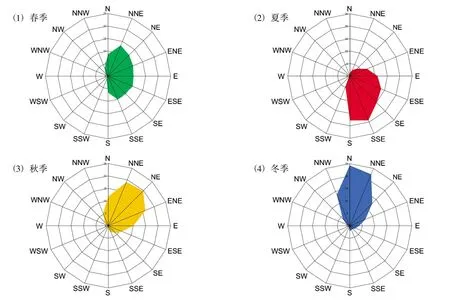
3 风速与波高的变化趋势
4 结论


