一篇文章中关于端点效应理论的修正证明及其应用举例
2020-12-11广东省中山市桂山中学528463余铁青
广东省中山市桂山中学(528463) 余铁青
一、问题提出
最近笔者在学习《中学数学教学》杂志2019年第6 期的文献时,发现当时湖北省黄石市第一中学杨瑞强老师的文章《端点效应破解恒等式问题》一文中存在叙述错误(具体错误请大家参考文献[1]).基于学习的初衷,笔者就此类问题进行了进一步的思考,给出了修正的结果,并进行了严格的证明.
近年来高考以及全国各地的模拟题中都出现了大量含参数恒成立问题,我们经常采用变量分离,等价转换等方法来进行解题.在使用这些做法解题中我们时常会遇到分类讨论情况多,我们可以说是不胜其烦,很难摆脱计算量大的困局,甚至最后不了了之,造成得分率较低的实际情况.笔者结合教学实际发现,在很多时候我们使用端点效应来解题效率会高得多,能够有效避免不必要的分层讨论,达到耗时少,得分多的效果.以下我们约定,文中所提及的有关函数的导数以及极限都存在.
二、端点效应的概念及修正证明
(一)端点效应的概念与适用范围
第一类: 若函数f(x,m)≥0(其中m为参数)在区间[a,b](a,b均为常数)上恒成立,且f(a)=0 或f(b)=0 则f′(a)≥0 或f′(b)≥0.此法应用于区间端点函数值为零的情况.[1]
结论处应修正为:f′(a)≥0 或f′(b)≤0.
第二类: 若函数f(x,m)≥ 0(其中m为参数)在区间[a,b](a,b均为常数)上恒成立,且或则f′′(x)≥0 或f′′(x)≥0[1].此法应用于区间端点函数值为零和端点一阶导数同时为零的情况.
此处结论应修正为:f′′(a)≥0 或f′′(b)≥0.
另外两种情况将一二类里面f(x,m)≥ 0 改为f(x,m)≤0 时的情形可以类比上述,进行等价转换,在此不再赘述.
(二)端点效应的理论证明
第一类情形的证明: 因为在区间[a,b](a,b均为常数)上f(x,m)≥0(其中m为参数)上恒成立,所以当x →a+时f(x)≥0;x →b−时f(x)≥0.结合f(a)=0 和导数的几何意义知:
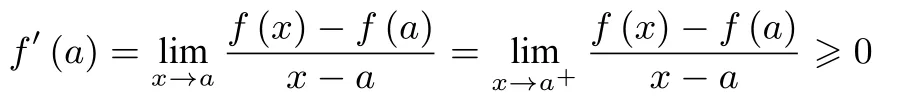
(具体理解可以参考文献[2],函数的右连续); 同理可证≤0(函数的左连续).
第二类情形的证明: 若函数f(x,m)≥0(其中m为参数)在区间[a,b](a,b均为常数)上恒成立去,为省去繁琐只证当则f′′(b)≥0.仿照上述证明因为
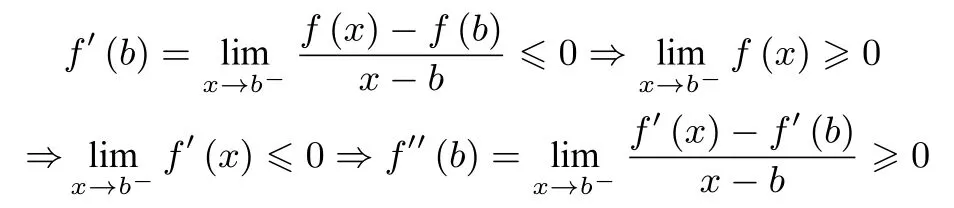
特别说明(1)上述证明的本质内涵实质是函数在区间端点处的左右导数(或二阶导数)问题,具体可以查阅参考文献[2],其次所给区间可以取开区间,利用极限即可处理.
(2)目前利用端点效应还只是解决了参数范围的必要性,还要证明充分性.直观的理解为: 第一步利用端点效应求出参数的具体范围;第二步将参数取值范围代入验证其正确性.
三、例说端点效应解题的优越性(第一类)
例1设a∈ℝ,已知函数f(x)=xlnx+ax2−(1+a)x+1,x∈(1,+∞).若f(x)>0 恒成立,求a的范围.
浙江省绍兴市柯桥区越崎中学的俞新龙老师在《恒成立问题中一类难点突破》[3]一文中给出了求解含参恒成立的几种常用方法.基于此认知,我们不妨对此题运用三种不同的方法来解,看看哪种策略更有优势.
解 方法1(等价转化法)令g(x)==lnx+ax+−(1+a),则原问题可以转化成g(x)>0 在x∈(1,+∞)恒成立.易知,
①当a≥0 时,g′(x)>0 在x∈(1,+∞)恒成立,即g(x)在x∈(1,+∞)单调递增,而且g(x)>g(1)=0 符合题意.
②当a≤时,g′(x)≤0 在x∈(1,+∞)恒成立,即g(x)在x∈(1,+∞)单调递减,而且g(x)<g(1)=0 不符合题意.
综上,参数a≥0.
方法二(参数分离法)由已知不等式f(x)>0 整理得对x >1 恒成立.设1),那么再 设h(x)=−2(x >1),则h′(x)=(x >1),当x∈(1,2)时,h′(x)<0,h(x)单调递减; 当x∈(2,+∞)时,h′(x)>0,h(x)单调递增,又h(1)=0,=+∞,即存在唯一x0>2 使得h(x0)=0.因此g(x)在区间(1,x0)递减,在(x0,+∞)上递增,又因为那么g(x0)≤g(x)<0.故a≥0.
方法三(端点效应法)由方法一和方法二知:f(1)=0.由于f′(1)=a以及f′(1)≥0,所以a≥0.所以a≥0 是原不等式成立的一个必要条件,下证充分性.
当a≥0 时,f′(x)=lnx+2ax −a,进一步f′′(x)=+2a,显然f′′(x)>0,那么f′(x)在(1,+∞)单调递增,且f′(1)=a >0,所以f′(x)>f′(1)>0 在x∈(1,+∞)上恒成立,所以f(x)>f(1),又结合f(1)=0,可知待证不等式成立.
评注分析对比三种不同解题方法可以发现以下几个问题: 第一,函数可以通过等价变化的形式来证明,此种方法有一定的思维难度,学生不一定能够想到;第二,此题第二种分离变量的策略是学生较为常用的方法,但在实际做题过程中经常会出现,分离参数后得到的新函数的导数表达式较为繁杂;第三种方法巧妙避开了讨论,使得整个体做起来更加顺畅高效,那么在教学中应更倾向于第三类解法.
四、端点效应再应用(第二类)
例2(2018 浙江镇海中学高三期中考试第21 题改编)函数f(x)=ex−1−x,当x >1 时,f(x)>m(x −1)lnx恒成立,求实数m的范围.
解令g(x)=ex−1−x −m(x −1)lnx,只需证明g(x)>0.显然g(1)=0,g′(x)=ex−1−1−mlnx −(x −1),此 时g′(1)=0,于是考虑求二阶导数得:g′′(x)=令g′′(1)≥0 得到
下证充分性.当m≤时,对g′′(x)求导,得到g′′′(x)=ex−1+下面分类讨论.①当0<m≤时g′′′(x)=ex−1+>0,因此g′′(x)=ex−1−在(1,+∞)上单调递增,于是g′′(x)=ex−1−>g′′(1)=1−2m≥0,同理分析可得g′(x)=ex−1−1−mlnx −(x −1)>g′(1)=0,那么g(x)在(1,+∞)上单调递增,所以g(x)>g(1)=0,于是0<m≤符合题意;
②当m≤0 时,f(x)=ex−1−x显然在(1,+∞)上大于零,而m(x −1)lnx在(1,+∞)上小于等于零,所以此时g(x)>0 依然成立.
综上,m≤证毕!
结语运用端点效应实质上是先给出必要性范围,再证充分性.很多时候能够大大减少分类讨论,有效提高解题效率,降低思维难度.教学中多思多想多总结是关键,力求做到精准解题,达到简洁高效的效果.
