数学建模视角下解决一道高中数学联赛的争议题*

2020-12-11广东仲元中学511400许鲔潮

中学数学研究(广东) 2020年21期

广东仲元中学(511400) 许鲔潮

广东番禺中学附属学校(511400) 麦桂崧

《普通高中数学课程标准(2017 版)》提出了数学学科核心素养,将学生的核心素养定义为“学生应具备的,能够适应终身发展和社会发展需要的必备品格和关键能力”[1].数学建模是六大核心素养之一,指对现实问题进行数学抽象,用数学语言表达问题、用数学方法构建模型解决问题,即在实际情境中从数学的视角发现问题、提出问题,分析问题、建立模型,确定参数、计算求解,检验结果、改进模型,最终解决实际问题[2].本文以2020年高中数学联赛浙江赛区初赛一道有争议的题目为起点,从数学核心素养出发,利用数学建模的思想和方法解决这道题并提出建议与改编.

一、问题的提出

题目某竹竿长为24 米,一端靠在墙上,另一端靠在地面上.若竹竿上某一节点到墙的垂直距离和到地面的垂直距离都是7 米,则此时竹竿靠在墙上的端点到地面的垂直距离为____米,或____米.

图1

本题是2020年6月21日举办的高中数学联赛浙江赛区初赛第3 题,分值8 分是一道中档题,但根据某学校学生的答题调查,只有10%左右的学生写出参考答案.

二、模型假设

(一)假定竹竿是正放,即竹竿在地面上的射影与墙面垂直;

(二)墙面及地面摩擦系数足够大,并且竹竿不会下滑;

(三)不考虑竹竿大小,重量及弹性形变等物理因素.

三、模型建立与求解

在模型假设的情况下,本题为平面几何问题,可建立如图1 的平面直角三角形模型,将题目抽象为: 己知ΔAOB为直角三角形,P点为斜边上一点,PM⊥OB于M点,PN⊥OA于N点,且PM=PN=7,AB=24,求OA的长度.不妨设OA=a,OB=b,依题意可得ΔANP与ΔAOB相似,可得化简可得

根据AB=24 可得a2+b2=242,可化为

由①,②可得a+b=25+7=32,ab=7×32,从而a,b为方程λ2−32λ+32×7=0 的两根,即16±由对称性可知OA的长度可能为a也可能为b,所以答案就是16+或16−

这个答案引发了不少质疑: 根据上面的模型假设竹竿是要正放,但题目中没有提及,是否还有其它的情况呢? 因为本题有较强的物理背景,我们尝试用实验进行验证,通过立体几何建模的方法对这个模型进行优化分析.

四、模型的验证及优化

(一)实验我们通过实物实验和计算机模拟实验进行验证.分别以吸管,普通2B 铅笔,质地均匀的木棍,铁棍以及计算机软件SolidWords 仿真模拟进行实验.实验设定及原理如下:

1.地面材料分别选择瓷砖(摩擦系数小),木地板(摩擦系数中等)和水泥地(摩擦系数大);

2.SolidWords 仿真模拟为了得到区分度较大的数据,我们将材料设置为超高密度的金属材料;

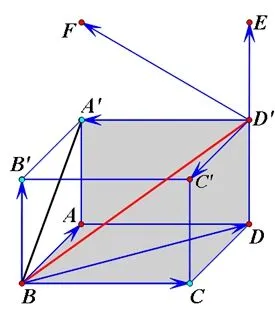
图2

3.利用手机软件“AR 测量”,通过如图2 中测量|AD|和|BD|的长度,计算出sin ∠ABD=所以(只取整数度数的角度).

在同一面墙壁上,多次重复实验得到如下实验结果:

_地面材料___吸管___铅笔___木棍___铁棍___SolidWords___瓷砖__________17° 22° 23° 13° 7°__木地板________22° 22° 24° 17° 9°__水泥地________35° 27° 27° 27° 14°

实验的结果显示存在稳定的倾斜放置.而且最大倾斜角度与物体的质量成负相关,与地面及墙面摩擦系数成正相关.

(二)模型拓展分析对竹竿进行受力分析如图2,竹竿B点处受到地面垂直向上的支持力及摩擦力其中可以分解为两个互相垂直的力同理,竹竿D′点处受到墙面垂直向外的支持力及摩擦力其中可以分解为两个互相垂直的力

(三)模型优化通过实验和竹竿受力分析,我们将模型优化为立体几何长方体模型,将竹竿理想化为长方体ABCD −A′B′C′D′的对角线BD′,竹竿上的点P到底面ABCD的距离为PM=7,点P到墙面ADD′A′的距离为PN′=7,竹竿的长度为BD′=24.以点B为坐标原点,以BC为x轴,BA为y轴,BB′为z轴建立空间直角坐标系,设BC=a,BA=b,BB′=c,BS=t则各点的坐标为B(0,0,0),C(a,0,0),A(0,b,0),B′(0,0,c),D′(a,b,c),P(t,b −7,7),则有由向量可得

由③式的第二个等号可得bc=7(b+c),联立a2+b2+c2=242可得a2+(b+c)2=242+14(b+c)化简可得a2+(b+c −7)2=252.

令a=25 cosθ≥0,而b ＞7,c ＞7 则b+c −7=25 sinθ ＞0,即b+c=7+25 sinθ,bc=7(7+25 sinθ)所以b,c为一元二次方程λ2−(7+25 sinθ)λ+7(7+25 sinθ)=0 的两个实数根.

结合判别式(7+25 sinθ)2−4×7(7+25 sinθ)≥0,解得sinθ∈,此时b,c有解.不妨设b ＜c则有

根据对称性,竹竿到地面的距离可以为c也可以为b,所以b,c两值就是题目的两解.所以符合题目的解有无数个,其中当a=25 cosθ=0 时,sinθ=1 则有b=16−c=16+这就是原模型的解答.

图3

图4

五、题目的优化与改编

(一)直接说明“正放”.例如: 某竹竿长为24 米,一端靠在墙上,另一端靠在地面上.使得竹竿在地面上的投影垂直于墙面.这样的说明可以让学生直接进入题目情景.

(二)与物理知识的结合.例如: 某竹竿长为24 米,一端靠在光滑的墙上,另一端靠在粗糙的地面上.这样的题设有一定的物理背景,由图2 受力分析可以知道,如果墙壁光滑没有摩擦力,则只有正放才能保持平衡.数学核心素养的本质,是描述一个人经过数学教育后应当具有数学特质,大体可以归纳为: 会用数学的眼光观察世界,会用数学的思维思考世界,会用数学的语言表达世界,简称“三会”[3].所以跨知识体系甚至跨学科的知识结合,也是数学核心素养的综合体现.

(三)构思新试题.原创题: 有一个长方体模型己知各边都为整数,对角线长度为39,且对角线上存在一点P到交于同一个顶点的三个侧面的距离分别为3,8,12,求这个长方体的体积.

分析本题入手简单,但错误率很高,主要原因是没有进行准确的分类讨论,对空间想象力和抽象逻辑要求较高.

解因为长方体的体对角线恒定,如图4,不妨设点P在对角线BD′上,设P到面ABB′A′的距离为3,P到面ABCD的距离为12,这时有两种情况:

(1)P到面BCC′B′的距离为8.

以点B为坐标原点,分别以BC,BA,BB′为x,y,z轴建立空间直角坐标系,设BC=a,BA=b,BB′=c,则点P的坐标为P(3,8,12),根据共线,所以D′(a,b,c)的坐标可设为D′(3θ,8θ,12θ),故|BD′|2=a2+b2+c2=217θ2,即θ2=不符合边长为整数的条件.

(2)P到面ADD′A′的距离为8.

点P的坐标为P(3,b −8,12),由向量可得可得c=4a,b=所以有