二面角中角的关系初探及应用

广州市第六中学(510300) 刘旭升

二面角中蕴含了很多的角,有二面角的平面角,直线与直线所成的角,直线与平面所成的角,那么这些角之间都有些什么关系呢? 下面我们一起来探究一下.

1.二面角与线线角的关系

如图1,给出大小为θ的二面角A −l −B.

图1

图2

如图2,在二面角的棱l上取点O,C,两个半平面内分别取射线OA,OB,设∠AOC=α,∠BOC=β,∠AOB=γ.则有

结论1(三面角的余弦公式)

特别地,当θ=90°,即两平面互相垂直时,cosγ=cosαcosβ.

限于篇幅,下面仅证明α,β均为锐角时,结论成立.

我们不妨设AC⊥CO,BC⊥CO,OC=1,则∠ACB=θ.易知AC=tanα,BC=tanβ,AO=secα,BO=secβ.ΔABC中,由余弦定理得

ΔAOB中,由余弦定理得

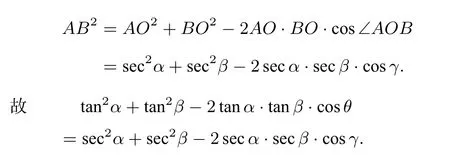
由sec2α=1 + tan2α,sec2β=1 + tan2β化 简 得secα·secβ·cosγ=1+tanα·tanβ·cosθ,同乘以cosα·cosβ得cosγ=cosαcosβ+sinαsinβcosθ.

注结论1 也称为三面角的余弦公式(见[1]).此外由异面直线所成的角的定义可知,当OA、OB改为两个半平面内任意一条直线时,该结论仍然成立.

2.二面角与线面角的关系

如图3,OA为二面角β −l −γ中面γ的一条射线.

图3

图4

结论2二面角β −l −γ的大小为θ,OA与面β所成角为φ,与棱l所成的角为α,则有sinφ=sinαsinθ.

证明: 如图4,过A点作AC⊥l于点C,作AB⊥β于点B,连BC,则由三垂线定理知∠ACB=θ,又∠AOB=φ.则sinφ==sinαsinθ.证毕!

结论3二面角β −l −γ的大小为θ,直线AB与棱l所成的角为α,与面β所成的角为φ1,与面γ所成的角为φ2,则有sin2θsin2α=sin2φ1+sin2φ2−2 sinφ1sinφ2cosθ.

图5

图6

证明如图6,作BG//l,取OA⊥l,OG⊥l交BG于点G,作AE⊥直线OG,作GF⊥直线OA垂足为F,BD⊥面γ且D∈ γ,则∠AOG=θ,∠ABG=α,∠ABE=φ1,∠BAD=φ2.取AB=1,则有AE=sinφ1,OA=AEcscθ=sinφ1cscθ;FG=BD=sinφ2,OG=FGcscθ=sinφ2cscθ.又AG=sinα,故ΔAOG中,由余弦定理得AG2=OA2+OG2−2OAOGcosθ,即有

整理得sin2θsin2α=sin2φ1+sin2φ2−2 sinφ1sinφ2cosθ.证毕!

注当φ2=0 时,结论3 即为结论2.

3.角间关系的应用

结论1 有广泛的应用,尤其在折叠问题中涉及角的问题,运用起来更是得心应手,很多问题均可轻松解决.下面我们看几道具体的问题.

例1(2015年高考浙江卷理科第8 题)如图7,已知ΔABC,D是AB的中点,沿直线CD将ΔACD折成ΔA′CD,所成二面角A′−CD −B的平面角为α,则( )

图7

A.∠A′DB≤αB.∠A′DB≥α

C.∠A′CB≤αD.∠A′CB≥α

解由结论1得到:cos ∠A′DB=cos ∠A′DCcos ∠BDC+ sin ∠A′DCsin ∠BDCcosα,由∠BDC=π −∠A′DC知cos ∠A′DB=−cos2∠A′DC+sin2∠A′DCcosα,因为

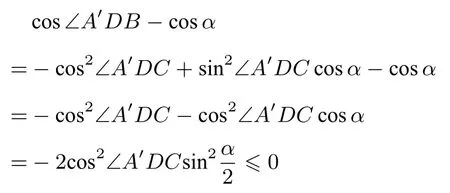
因此cos ∠A′DB≤cosα,故∠A′DB≥α,选B.选项C、D也可用此公式排除.

例2(2018年浙江高三月考)已知ΔABC,D是边BC(不包括端点)上的动点,将ΔABD沿直线AD折起到ΔAB′D,使B′在平面ADC内的射影恰好在直线AD上,则( ).

A.当BD=CD时,B′,C两点的距离最大

B.当BD=CD时,B′,C两点的距离最小

C.当∠BAD=∠CAD时,B′,C两点的距离最小

D.当BD⊥AD时,B′,C两点的距离最大

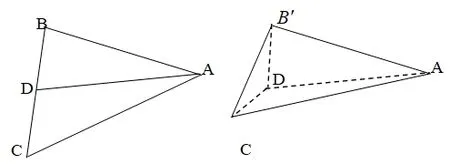
图8

解由于B′C ＜B′D+DC=BC,故B′,C两点的距离没有最大值.又依题可知二面角B′ −AD −C为直二面角,故由结论1 得cos ∠B′AC=cos ∠B′ADcos ∠DAC.ΔB′AC中,由余弦定理可得

因此当cos(∠B′AD −∠DAC)取最大值1 即∠B′AD=∠DAC即∠BAD=∠CAD时,B′C有最小值.故选C.

例3(2019年湖南高三开学考试(理))已知ΔABC是由具有公共直角边的两块直角三角板(RtΔACD与RtΔBCD)组成的三角形,如图9(左图)所示.其中,∠CAD=45°,∠BCD=60°.现将RtΔACD沿斜边AC进行翻折成ΔD1AC(D1不在平面ABC上).若M,N分别为BC和BD1的中点,则在ΔACD翻折过程中,下列命题不正确的是( )

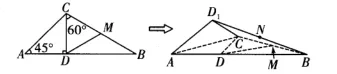
图9

A.在线段BD上存在一定点E,使得EN的长度是定值

B.点N在某个球面上运动

C.存在某个位置,使得直线AD1与DM所成角为60°

D.对于任意位置,二面角D1−AC −B始终大于二面角D1−BC −A

解对于选项C,设直线AD1与DM所成的角为θ,二面角D1−AC −B的大小为α,由条件可知AD1与AC所成的角为45°,DM与AC所成的角为15°.由结论1 知cosθ=cos 45°cos 15°+ sin 45°sin 15°cosα,因为0° ＜α ＜180°,因此−1＜cosα ＜1,因此cos 45°cos 15°+sin 45°sin 15° ＞cosθ ＞cos 45°cos 15° −sin 45°sin 15°,即cos 30° ＞cosθ ＞cos 60°,因此30° ＜θ ＜60°.故选C 选项.

从以上几个例子我们可以看出结论1 在解决折叠图形中有关角问题的便捷性,该结论同样可以用在解决三棱锥中的某些角的问题.而结论2 在解决有关线面角问题也能取得不错的效果.我们看几道模拟题.

例4(2019年河北高一期末考试)在ΔABC中,AB=2BC,将ΔABC绕BC所在直线旋转到ΔPBC,设二面角P −BC −A的大小为θ(0＜θ ＜π),PB与平面ABC所成角为α,则α的最大值为( )

解由结论2 知sinα=sin ∠PBCsinθ=≤故角α的最大值为

图10

图11

例5(2020年浙江高三二模试题)在四面体S −ABC中,点P在线段SA上运动(不含端点).设PA与平面PBC所成角为θ1,PB与平面SAC所成角为θ2,PC与平面ABC所成角为θ3,则( )

A.θ2＜θ1＜θ3B.θ2＜θ3＜θ1

C.θ3＜θ1＜θ2D.θ3＜θ2＜θ1

解取S −ABC为正四面体,则每两个面所成的角均相同,设为α.记二面角A −PB −C的大小为β,由图11 可知β ＞α.由结论2 知sinθ1=sin ∠APBsinβ,sinθ2=sin ∠APBsinα,sinθ3=sin ∠ACPsinα,易证∠APB=∠APC ＞60° ＞∠ACP,故sinθ1＞sinθ2＞sinθ3,从而θ3＜θ2＜θ1,选D.