模糊区间值截距阵[D][a,b]的若干性质
2020-12-10关却东智更芷拉毛索南仁欠
关却东智,更芷拉毛,索南仁欠,2*
(1.青海师范大学 数学与统计学院,青海 西宁 810008;2.青海师范大学 研究生院,青海 西宁 810008)
由于客观事物的复杂性和不确定性,以及人类思维的模糊性和有限性,人们往往不能明确地给出具体数值,只能给出一个区间范围,这种区间范围是以区间值(或区间数)的形式来表示。区间值代表了一种不确定性,目前在许多领域都有着很大的应用潜力。例如,利用区间值进行不确定的多属性决策,将区间值添加到数学规划之中形成不确定性优化模型,模糊区间值综合决策模型,等等。其中的模糊区间值综合决策是近年来发展较为成熟的一种模糊数学方法,它广泛应用于环境质量评价、气象预报、经济管理及教学过程的评价等领域。
Moore最早提出并深入研究了区间值,给出了相关运算性质和区间值间的排序方法[1]。而Moore定义的排序方法无法比较具有交叉重叠时的区间值排序问题。之后,曾文艺等[2]利用区间值平均法给出排序方法,Sengupta和Pal[3]基于序关系给出区间值排序法,刘进生等[4]定义了一种比较区间值的度量函数,还有赵慧冬等[5]的几何平均排序函数。李德清等[6]系统梳理了常用的区间数排序方法,详细介绍了每一类排序方法的主要思想,分析了每种方法的特点和不足,特别是在已有的基础上深入讨论了基于可能度矩阵的区间数排序方法。区间值排序方法针对不同实际问题的需要,还有很多有特色的排序方法。近年来,很多国内外专家将区间值引入模糊数学,构建了特色的模糊区间值理论。但是,应用上述排序方法比较模糊区间值会带有不同程度的过拟合和欠拟合现象。排序方法最终目的是描述两区间数间的相似和贴近度大小,从而刻画决策者的心态偏好。
为了准确反映模糊区间值矩阵与模糊决策者心态(模糊区间阈值)偏好等问题,本文给出了一种排序函数,用来比较模糊区间值,并利用这种方法定义模糊区间值矩阵的[a,b]-截距阵。排序函数比较法将模糊区间值映射到模糊矩阵对应排序函数图像的坐标轴上后,再利用优劣度、交点、信度等概念,把模糊区间值矩阵转化为模糊矩阵,并用模糊矩阵的相关性质和处理方法解决实际模糊区间值矩阵问题,而模糊矩阵的截距阵已有广泛研究和应用。本文通过研究优势、劣势、信度的度量值来等价转化为模糊区间值,最后得到模糊矩阵的相关代数性质。本文也给出了一些例子说明优势、劣势和信度的度量值评价决策偏好的可行性。
1 预备知识
定义1(模糊区间值)[7]若[A]=[a-,a+],对于任意的a-,a+满足0≤a-≤a+≤1,则称[A]为模糊区间值,其中,a-为下元,a+为上元。模糊区间值[a,a]=a(等同于数a,且a∈[0,1])。记全体模糊区间值构成的集合为I。
模糊区间值是区间值的数值限制在[0,1]中的特殊区间值,同时,模糊区间值具有如下独异的运算方法。
定理1(模糊区间值的相关运算)[8]设区间值[A]=[a-,a+],[B]=[b-,b+],则有如下运算规则:
1) [A]∧[B]=[a-∧b-,a+∧b+]=
[min(a-,b-),min(a+,b+)]
2) [A]∨[B]=[a-∨b-,a+∨b+]=
[max(a-,b-),max(a+,b+)]
3) [A]+[B]=[a-+b-,a++b+]
4)k[A]=[ka-,ka+],(k>0)
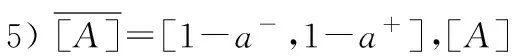
6) [A]=[B],当且仅当a-=b-,a+=b+。
定义2(同态映射)[9]设G,S是在*与∘运算下具有封闭性和结合律的代数系统,δ是从G到S上的映射。若a,b∈G满足
δ(a*b)=δ(a)∘δ(b)
则称δ是G到S的同态映射,简称G与S同态。
1) 若δ是单射,则称G与S单同态。
2) 若δ是满射,则称G与S满同态,记作G~S。
3) 若δ是双射,则称δ是G到S的同构映射,并称G与S同构,记作G≅S。
定义3(序关系)[8]设是I上的一个二元关系,对于任意区间值[A]=[a-,a+],[B]=[b-,b+],若满足下面6条性质,则称为上的一种序关系。
1) 自反性:[A][A]。
2) 传递性:若[A][B]且[B][C],则[A][C]。
3) 完全性:对任意的[A],[B]∈I时,一定有[A][B]或者[B][A]。
4) 分离性:若a-≤b-,则[A][B]。
5) 相容性:若[A][B],则当[A],[B]∈I时,一定有[A]≤[B]。
6) 线性性:若[A][B],则对于任意的[C]∈I及实数k≥0,一定有
[A]+[C][B]+[C],k[A]k[B]。
定义4(二元运算)[9]设S是一个非空集合,S×S到A的映射成为S上的二元运算。
一般地,Sn到S的映射成为S上的n元运算。
定义5(代数系统)[9]设非空集合S,则S上k个一元或二元运算f1,f2,…,fk组成的系统称为代数系统,记作〈S,f1,f2,f3,…,fk〉
2 模糊区间值截距阵的定义及若干性质
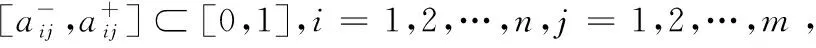
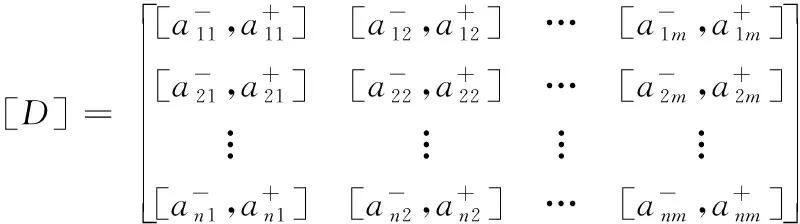
则称[D]为模糊区间值矩阵。
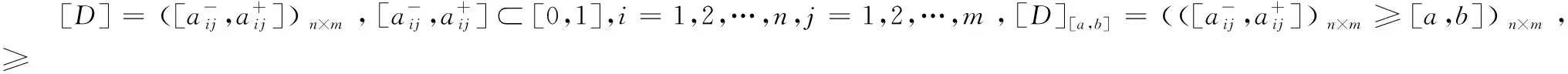
定义8[10]对于任意的模糊区间值[A]=[a-,a+],则称
f[A](x)=a-+(a+-a-)x,x∈[0,1]
为模糊区间值[A]的排序函数。
定义9[11-12]对于任意的模糊区间值[A]=[a-,a+],[B]=[b-,b+],则
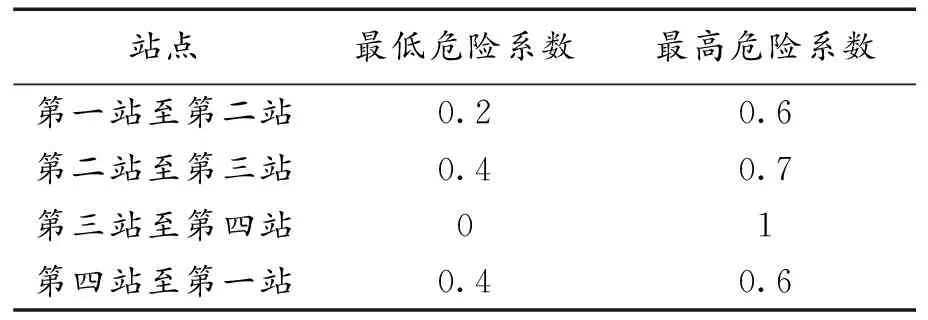
1)若模糊区间值的排序函数f[A](x) 2)若模糊区间值的排序函数f[A](x)>f[B](x),则称模糊区间值[A]优于[B]。 3)若模糊区间值的排序函数f[A](x)=f[B](x),则称模糊区间值[A]等于[B]。 定理2[13-14]对于任意的模糊区间值[A]=[a-,a+],[B]=[b-,b+],([A]≠[B])则 1) 排序函数f[A](x)单调非减函数。 2) 排序函数f[A](x),f[B](x)图象至多一个交点,简称交点。 3) 交点的横坐标为 证明1) 排序函数是定义域为x∈[0,1]的一次函数,且斜率为正,即a+-a-≥0,故排序函数为单调非减函数。 2) 排序函数定义域x∈[0,1]内的交点可分为如下不同情形; 情形一:a+-a-=b+-b-时,无交点。 情形二:a-=b-,a+-a-≠b+-b-时,下元为交点。 情形三:a+=b+,a+-a-≠b+-b-时,上元为交点。 综上所述,排序函数的交点要么在定义域内,要么在定义域外(不作考虑),因此,排序函数f[A](x),f[B](x)图象至多一个交点。 定义10 1)设[D]表示模糊区间值矩阵,从优势程度的角度,则可得[D]的[a,b]-截距阵, 2)设[D]表示模糊区间值矩阵,从劣势程度的角度可得[D]的[a,b]-截距阵,则有 3)设[D]是m×n阶模糊区间值矩阵,从[D]中元素优于[a,b]的可信角度可得[D]的[a,b]-截距阵,且有 以上三种定义方式各有特点,可用来刻画模糊区间值相似、大于或优于(小于或者劣于,两者综合应用)另一个区间值的程度,这种程度恰好可以反映决策者的偏好信息。 adv[D][a,b]和Inf[D][a,b]是[a,b]在排序函数f[D](x)上的纵坐标轴投影,表明其模糊区间值[a,b]在[D]上的截距阵。此时,截距阵表示模糊区间值矩阵与模糊区间值之间的优劣程度或者相似程度,而rel[D][a,b]是两种排序函数f[D](x)在横坐标轴的投影,表示两种排序函数在[x*,1]上的同时射影,这是一种互为条件,互相影响的模型。前两种是主因素突出时应用效果较好,后一种rel[D][a,b]信度矩阵,它的模糊程度较高,在各因素都起作用时应用效果较好。 例1 [D]表示模糊区间值矩阵 模糊区间值[0.4,0.6]处的三种定义下的截距阵。 在模糊区间值[0.4,0.6]处的排序函数f[0.4,0.6](x)=0.2x+0.4,在模糊区间[0.4,0.7]处的排序函数值f[0.4,0.7](x)=0.3x+0.4,在模糊区间值[0.3,0.5]处的排序函数f[0.3,0.5](x)=0.2x+0.3,在模糊区间值[0,1]处的排序函数为f[0,1](x)=x,则根据定义10,在定义域[0,1]内f[0.4,0.7](x)>f[0.4,0.6](x)时取1,在定义域[0,1]内f[0.3,0.5](x)>f[0.4,0.6](x)时取0,在定义域[0,1]内{>x*|f[0,1](x)=f[0.4,0.6](x)}时交点为0.5,再代入 有δ=0.5,因此如上算法可得用优势能度衡量的[D]的截矩阵为 劣势度衡量的[D]的截矩阵为 则信度衡量的[D]的截矩阵为 由上例可知,信度矩阵计算简单,是劣度和优度的综合体现,不过也有部分缺点,若排序函数图像斜率一致时,信度将它收缩为零,这是不符合实际的。因此,应该结合优度和劣度矩阵对问题进行分析。 定理3 三种定义下模糊区间值矩阵对于≥[a,b]在I上具有序关系。 证明1) 自反性:[A][a,b]≥[A][a,b]。 2) 传递性:若[A][a,b]≤[B][a,b]且[B][a,b]≤[C][a,b],则[A][a,b]≤[C][a,b]。 3) 完全性:对于任意[A][a,b]与[B][a,b],必有[A][a,b]≤[B][a,b]或者[A][a,b]≥[B][a,b]。 4) 分离性:若a+≤b-,则区间数定义的a-≤a+≤b-≤b+,从而有 [a-,a+][a,b]≤[b-,b+][a,b] 5) 相容性:若[a-,a+][a,b]≤[b-,b+][a,b],则必有[a-,a+]≤[b-,b+] 6) 线性性:若[a-,a+][a,b]≤[b-,b+][a,b],则对任意的[c-,c+][a,b]及实数k>0,一定有[a-,a+][a,b]+[c-,c+][a,b]≤[b-,b+][a,b]+[c-,c+][a,b] k[a-,a+][a,b]≤k[b-,b+][a,b] 所以≥[a,b]是I上的序关系。 ii) 0≤rel[D][a,b]≤1,0≤adv[D][a,b]≤1,0≤Inf[D][a,b]≤1 证明这里仅证明3),其他结论显然成立。 f[a-,a+](x)与f[a,b](x)交点为 定理5 [D]表示模糊区间值矩阵,A表示任意模糊矩阵。代数系统〈[D],+〉和〈A,+〉,δ表示rel[D][a,b],adv[D][a,b],Inf[D][a,b],是从[D]到A上的映射,若[a,b],[c,d]∈[D],则 δ([a,b]+[c,d])≠δ([a,b])+δ([c,d]),0≤[a,b]+[c,d]≤1 δ(k[a,b])≠kδ([a,b]),(k>0) 所以对于加法与数乘,rel[D][a,b],adv[D][a,b],Inf[D][a,b]不是[D]到A的同态映射。其中,[D]表示模糊区间值矩阵,A表示任意矩阵。 证明(反证法) 0≤δ([a,b]+[c,d])≤1,而0≤δ([a,b])+δ([c,d])≤2,由此可知代数系统〈[D],+〉和〈A,+〉在δ下不封闭。因此,δ([D])不一定是A的子集。由此可知,等号不成立。 同理可得,以下推论。 1)当[D1]不管大于、小于、等于[D2]都有 {>[D1]∨[D2]}[a,b]=[D1][a,b]∨[D2][a,b] 2)当[D1]不管大于、小于、等于[D2]都有 {>[D1]∧[D2]}[a,b]=[D1][a,b]∧[D2][a,b] {>[D1]∨[D2]}[a,b]≥[D1][a,b]∨[D2][a,b] {>[D1]∧[D2]}[a,b]≤[D1][a,b]∧[D2][a,b] 定义11 设rel[D][a,b],adv[D][a,b],Inf[D][a,b]分别是优度截矩阵,劣度截矩阵,信度截矩阵,则有 定义12 若综合信度(优度)决策指数λ越低,决策偏好越低,若综合信度(优度)决策指数λ越高,决策偏好越高。 若综合信度(优度)决策指数λ=0.5,决策偏好中庸。相反,若综合劣度决策指数λ越低,决策偏好越高,若综合劣度决策指数λ越高,决策偏好越低。 若综合劣度决策指数λ=0.5,决策偏好中庸。 在模糊综合决策中,阈值相当重要,它既反映各个因素在模糊综合决策中占据的地位或者影响其决策结果的程度,又反映着决策时的决策者的心态偏好指数。 例2 一辆公交车经过四站点,期间出事故程度,如表1所示。 表1 站点间危险度表 则危险系数区间值矩阵为 有δ=0.5,所以模糊区间值矩阵优度截矩阵为 模糊区间值矩阵劣度截矩阵为 而根据信度矩阵定义有,在定义域[0,1]内min{>x*|f[0.4,0.7](x)>f[0.4,0.6](x)}时取0,在定义域[0,1]内min{x*|f[0.3,0.5](x) 根据三个截矩阵判断,模糊区间值[0.4,0.6]为阈值时,对整体影响较小,不可避免的去掉这种情形。综合优度决策指数为0.3125,综合劣度决策指数为0.6875,综合信度决策指数为0.1875,三种综合决策说明危险系数限制在0.4至0.6间是不合理的。 本文为解决模糊区间值矩阵信息不完全时不能准确反映模糊决策者的心态偏好,将排序函数作为两个区间值之间的距离函数或者相似函数,来定义模糊区间值矩阵的截距阵,进一步利用两区间值的优势程度、劣势程度、相信程度衡量两者的优于(相似)程度,从而用其描述偏好程度关系。具体是将模糊区间值和排序函数映射到模糊矩阵对应的排序函数坐标轴上,进而将模糊区间值矩阵转化为模糊矩阵,并用模糊矩阵的相关性质和处理方法解决实际问题。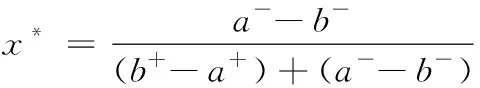

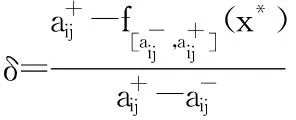
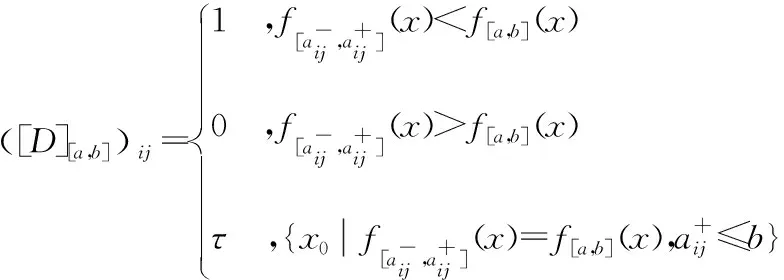
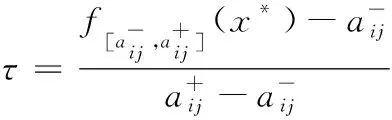
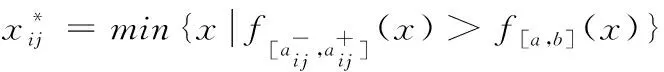
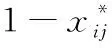

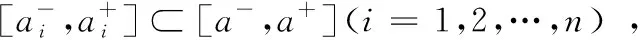
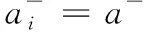
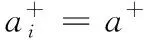
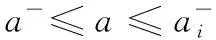

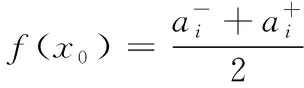
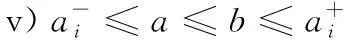
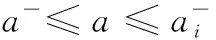
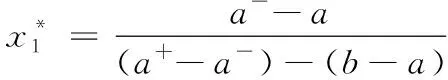
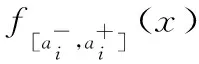
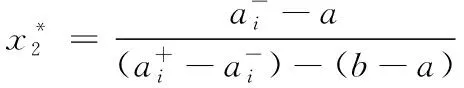
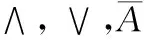
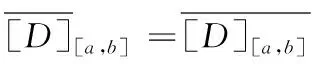
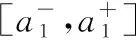
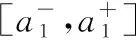
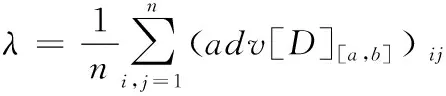
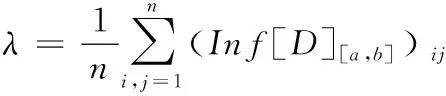
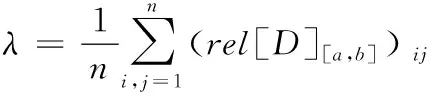

3 总结
