隧道掘进爆破时掌子面前方开挖段的地表振速预测

陈经鹏，陈士海,2

(1. 华侨大学 土木工程学院，福建 厦门 361021；2. 福建省隧道与城市地下空间工程技术研究中心，福建 厦门 361021)

在我国城市基建高速发展的背景下，各大城市对交通建设也提出了更高的要求.地铁由于其运行速度快、输送量大的特点，已逐渐成为一个城市发展建设程度的标志性工程，越来越受到城市建设者们的重视.我国地铁隧道开挖技术已较为成熟，但多数情况下考虑到经济等因素，建设者们会选择矿山法进行施工.我国城镇具有人口分布集中、交通线密集的特点，在地铁建设中，地铁线路难免会下穿一些重要设施，而隧道在掘进爆破的过程中，对地面的一些敏感设施造成影响，甚至对地面的建构筑物产生损坏.因此，研究爆破时的地表震速是很有必要的.

随着我国隧道工程建设的开展，我国工程技术人员也对工程中出现的各类问题进行了大量的研究.曹孝君等[1]对地表振速分布规律进行了数值模拟研究，其模拟分析结果与实际监测结果较为一致.杨甲豹[2]通过数据回归分析，并结合实时监测数据，不断调整爆破参数设计，从而达到控制爆破震速的目的.傅洪贤等[3]在研究爆破近区的振动规律时，运用简化药包的方法.刘小鸣等[4-5]求出实际介质中球形药包地表振速函数，建立掏槽孔爆破隧道未开挖段上方的地表振动预测方法，得到单孔柱状药包爆破引起的半空间中地表振速函数.张继春等[6]发现地表振速受掏槽孔爆破影响最大，且发现挖空段上方的地表振速存在“空洞效应”.郭建群等[7]发现隧道未开挖段地表振速和已开挖段地表振速之间的关系.杨云凌[8]通过数值模拟发现隧道挖空段的地表振速存在放大现象，且该现象受到隧道埋深的影响.宋杰[9]发现在爆破近区，振速放大系数随纵向距离的增加有先增加后减少的现象.闫兵等[10]建立不同弹性模量工况情形下的三维多场耦合模型，发现空洞效应具有一定的区域性，在爆心距0～80 m范围内均有可能产生隧道空洞放大效应，且围岩的性质会对该现象产生一定影响.宗琦等[11]通过监测数据也发现从工作面后方到工作面前方，地表质点振动峰值速度先增大后减小，有空洞效应现象.李建旺[12]发现在掌子面前后10 m范围内，隧道已开挖段地表振速有空洞效应[13-15].李胜林等[16]运用萨道夫斯基公式和日本株式会社公式对掌子面前方隧道未开挖段地表振速进行预测，并与实际监测数据进行对比研究.袁旺小[17]运用应力波斜入射地表面的相关理论，对隧道掘进爆破时未开挖段地表振速进行预测.谢烽等[18]运用波形叠加原理，对掌子面后方的隧道已开挖段振动规律进行模拟.

目前，针对隧道未开挖段地表振速问题和掌子面后方隧道开挖段地表振速预测问题的研究较多，而对于隧道双向掘进到一定程度时的掌子面前方开挖区段的地表振速问题研究较少，在爆破近区的隧道成洞区地表振速存在不同程度的放大效应.福建省厦门市轨道交通3号线创业桥站-安兜站下穿鹰厦铁路，铁路位于掘进掌子面的前方且下方存在一定长度的挖空部分，隧道掘进爆破势必会对地表铁路造成影响.因此，本文从理论方面对掌子面前方涉铁段隧道的地表质点振速进行提前预测，以实现爆破优化设计，确保铁路运行安全.

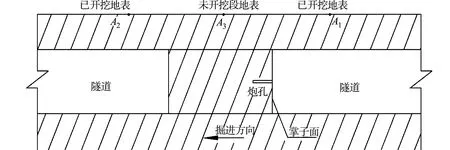
图1 隧道掘进爆破振动模型Fig.1 Vibration model of tunnel excavation blasting

1 隧道爆破振动理论模型

根据地表质点在空间中的具体位置，振动问题可分为隧道未开挖段地表质点问题和隧道已开挖段地表质点问题，隧道掘进爆破振动模型，如图1所示.

隧道掌子面在掘进爆破时，一般均由一组掏槽孔先行爆破，受孔数及孔距的影响，计算爆破振速较为困难.因此，将一组掏槽孔的爆破问题简化为单孔柱状药包的爆破问题，以实现理论计算的简便化.根据药包简化前、后的装药长度和总装药质量不变的原则[3]，可将一组掏槽孔转化为单孔柱状药包，并将单孔柱状药包转化为m个等效球形药包的叠加.转化原则为：转化前、后总装药质量不变，m个等效球形药包的直径之和等于柱状药包的装药长度，有

上式中：rc为柱状药包半径；re为等效球形药包半径.

等效球形药包,如图2所示.图2中：l1为炮泥长度;xi为起爆点到第i个等效球形药包中心的距离，i=1,2,…,m.隧道掘进中的等效球形药包，如图3所示.

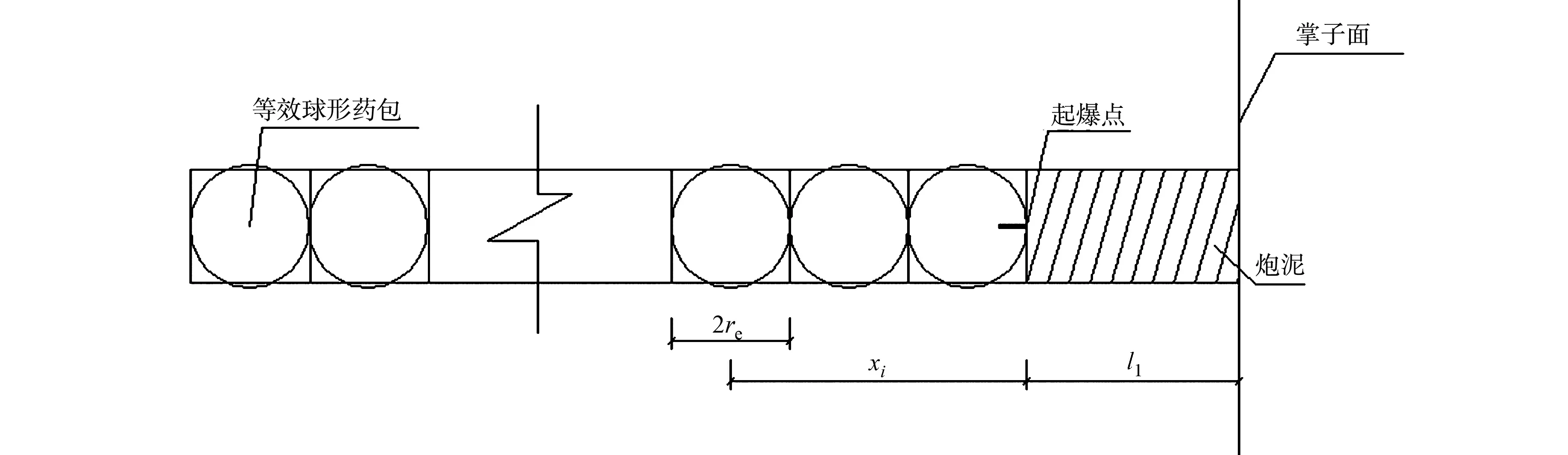
图2 等效球形药包Fig.2 Equivalent spherical charge

图3 隧道掘进中的等效球形药包Fig.3 Equivalent spherical charge in tunnel excavation

等效球形药包i是指第i个起爆的等效球形药包，等效球形药包i引起的半空间中地表质点振速函数已由刘小鸣等[5]求出.等效球形药包i爆炸会引起隧道已开挖区段地表质点A1和A2的振动，以及隧道未开挖区段地表质点A3的振动，再将m个等效球形药包引起的地表质点振速函数进行叠加，在地表质点A1，A2和A3叠加后的振速函数即为简化得到的单孔柱状药包爆破在该点引起的振速函数，最终即可得到隧道掘进爆破引起的地表质点振速函数.

2 隧道未开挖区段的地表质点振速

对于隧道未挖通段的地表质点A3而言，振动波在等效球形药包i及其之间的传播不受隧道空洞的影响，地表质点振速可按半空间中的地表质点振速方法计算，半空间中球形药包爆破在地表质点产生的振速函数[4]为

(1)

式(1)中:Q为球形药包的装药质量，kg；R为球形药包至地表质点的距离，m；振速衰减指数β=100-RMR,RMR为岩石的分级评分；α为与岩体类型相关的参数.

表1 不同类型岩体的RMR,βTab.1 RMR, β for different rocks

不同类型岩体的RMR,β,如表1所示.振动频率为

上式中：k，α根据具体工程地质条件取值，岩石k=30～70，风化岩石k=70～150，土壤k=150～250，岩石风化程度越严重，k越大，不论岩石还是土壤，α=1～2，岩体越完整，α越小.

对于单孔柱状药包所等效的m个球形药包而言，必须考虑球形药包爆破时药包之间的相互影响，这种影响刘小鸣等[5]已通过添加系数的方法在振速函数中予以体现.具体振速函数为

(2)

地表质点A3的振速按半空间理论进行计算，可以先求第i个球形药包在该点引起的振速函数，隧道未开挖区段振速模型，如图4所示.

图4 隧道未开挖区段振速模型Fig.4 Vibration velocity model in unexcavated section of tunnel

图4中：xl为未开挖区段地表质点A3至掌子面的距离；r为等效球形药包i至隧道顶面的距离；h为隧道上顶面至地表的距离.

第i个球形药包至点A3的距离Ri为

(3)

将式(3)的Ri及具体工程中的相关参数带入式(2)计算，即可得到第i个球形药包在点A3引起的振速函数.地表质点A3在任意时刻t由简化柱状药包爆炸所引起的振速函数为

.

(4)

3 隧道已开挖区段地表质点振速

3.1 点A2振速

隧道已开挖区段振速模型，如图5所示.图5中：l为隧道未挖通段长度；di为等效球形药包i至隧道掌子面的距离；d为掌子面前方开挖段地表质点至未开挖段的水平距离；x为掌子面后方开挖段地表质点至掌子面的水平距离.

图5 隧道已开挖区段振速模型Fig.5 Vibration velocity model for excavated section of tunnel

对于已开挖区段的地表质点A2而言，由于地表质点下方的隧道区段已经挖空，挖空段势必会对振动波的传播造成影响，无法直接利用上述理论计算该点的振速函数.因此,通过映射函数将隧道已开挖段上顶面点B2和等效球形药包i的位置关系映射为半平面空间中的位置关系，继而可求出点B2和等效球形药包i之间的等效直线传播距离，最后,将该等效直线距离加上h，就可得到点A2与等效球形药包i之间的等效直线传播距离.

图6 z平面上的隧道爆破简化模型1Fig.6 Simplified model 1 of tunnel blasting on plane z

考虑点B2的振动效应，需要求等效球形药包i与隧道开挖段上顶面点B2的等效直线传播距离，假设隧道顶面和空洞部分是无限延伸的，即暂不考虑隧道空洞底部和地表对点B2振速的影响，建立z平面上的隧道爆破简化模型1,如图6所示.

通过映射函数，将图6的爆破问题转化为w平面上的隧道爆破简化模型1，如图7所示，从而实现复杂边界条件向简单边界条件的转换.

通过复变函数可求出图6模型的映射函数，即

w=z1/2

.

(5)

(6)

图7 w平面上的隧道爆破简化模型1Fig.7 Simplified model 1 of tunnel blasting on plane w

由式(5)，将药包i映射到w平面中，其坐标表示为

(7)

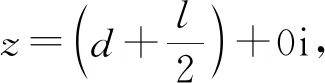
(8)

由式(5)，将B2点映射到w平面中，其坐标表示为

(9)

由复变函数可知,该点位于w平面中的横轴正半轴上.

(10)

(11)

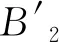
振动波由B2传到A2后，在A2和B2之间还会继续发生反射，但振动波在各地层之间发生的反射会不断衰减，衰减后的振动波在地表叠加时，对地表质点的振速影响较小，且影响振动波反射的因素很多，很难从理论方面进行量化分析，故暂不考虑振动波的反射叠加作用.

等效球形药包i与隧道开挖段地表质点A2的等效直线传播距离为

(13)

将对应的Ri带入式(2)，(4)，并根据叠加原理，即转换得到半空间中m个等效球形药包引起的地表质点振速函数，即隧道掘进爆破时，掌子面前方开挖段的地表质点A2的振速函数.

图8 z平面上的隧道爆破简化模型2Fig.8 Simplified model 2 of tunnel blasting on plane z

3.2 点A1振速分析

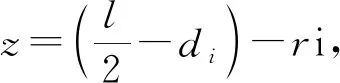
由式(5)，将药包i映射到w平面中，其坐标表示为

(14)

由复变函数可知，该点位于w平面中的第二象限.

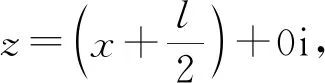
(15)

由式(5)，将B1点映射到w平面中，其坐标表示为

(16)

由复变函数可知，该点位于w平面中的横轴正半轴上.

因此，可以得到w平面中的隧道爆破简化模型2，如图9所示.

图9 w平面上的隧道爆破简化模型2Fig.9 Simplified model 2 of tunnel blasting on plane w

(17)

(18)

由式(13)可计算Ri，将Ri与各计算参数带入式(2)，并根据式(4)对m个振速进行叠加，即可求出地表质点A1的振速函数.

4 工程实例计算与分析

以厦门市轨道交通3号线创业桥站-安兜站区间涉铁段为研究对象，计算预测隧道轴线地表质点振速峰值.地铁区间下穿铁路平面示意图，如图10所示.

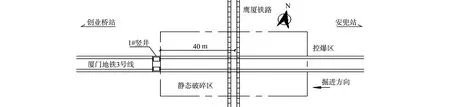
图10 地铁区间下穿铁路平面示意图Fig.10 Schematic diagram of subway section crossing railway

为确保铁路安全，下穿铁路段采用静态破碎法施工，静态破碎法施工范围为铁路线路中心线两侧各38.8 m，共77.6 m；根据铁路运营需要，为保证列车运行安全，铁路中心线两侧各100 m的范围内(除静态破碎施工范围)选用封锁点控制爆破施工，下穿铁路距离铁路中心线前、后100 m的范围内，铁路路基的振速控制在2 cm·s-1以内.

铁路为有砟轨道，拟建区间场区地的基土以稳定基岩和中硬土为主，地层结构自上而下依次为：素填土、粉质黏土、散体状强风化花岗岩、碎块状强风化花岗岩、中等风化花岗岩、微风化花岗岩.爆破点与监测点之间的地层结构参数,如表2所示.表2中：H为土层厚度；υ为泊松比；E为弹性模量；ρ为密度.

由表2可知：弹性模量的加权平均值为42 MPa;泊松比的加权平均值为0.25;密度的加权平均值为2 000 kg·m-3.弹性模量、泊松比与密度用于计算p波在介质中的传播速度cp.计算区间的隧道围岩为Ⅳ级中等风化花岗岩，Ⅰ～Ⅱ级微风化花岗岩.相关区间隧道采用矿山法施工，洞径约6.2 m，共掘进总长度约1 077.4 m.地铁区间隧道顶面距铁路路基的垂直距离为15.1 m.

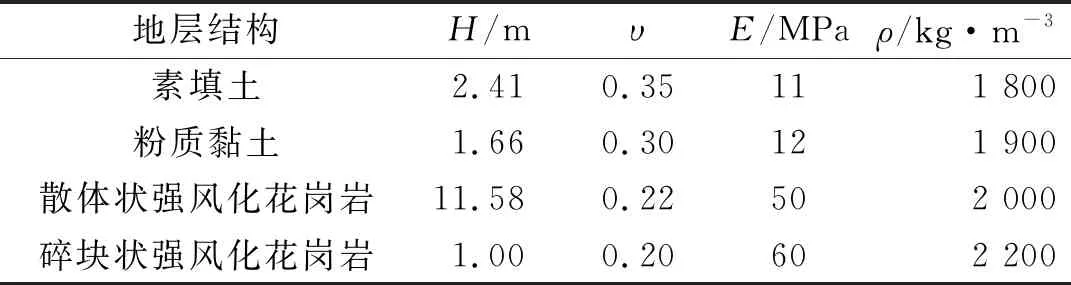
表2 场区的地层参数Tab.2 Stratigraphic parameters in site

控爆区采用2号岩石乳化炸药，炸药的密度为1 243.4 kg·m-3，爆速为3 500 m·s-1，距离铁路中心前、后100 m范围内用数码电子雷管，距离铁路中心前、后100 m范围外用毫秒延期非电导爆管雷管.

案例选取2019年10月20日-2019年10月22日的爆破数据进行分析计算，爆破参数如表3所示.表3中：s为起爆掌子面里程数；D为孔深；m1为单孔装的质量；m2为掏槽孔装药质量；vmax为测量的最大振速.

表3 爆破参数Tab.3 Blasting parameters

根据模型的简化方法可知：2019年10月20日掏槽孔的爆破简化成半径为0.032 m、长度为1.5 m的简化柱状药包，该简化柱状药包又可划分为20个半径为0.039 m的等效球形药包，单个等效球形药包质量为0.3 kg；2019年10月21日—2019年10月22日掏槽孔的爆破简化成半径为0.039 m、长度为1.5 m的简化柱状药包，该简化柱状药包又可划分为15个半径为0.048 m的等效球形药包，单个等效球形药包质量为0.6 kg.监测仪器布设在铁路路基上，仪器编号为L20-N22129.由于该项目的特殊性，案例选取掌子面前方地表质点A2的振速进行预测，案例模型图，如图11所示.

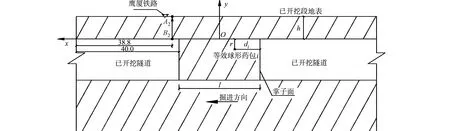
图11 案例模型图(单位：m)Fig.11 Case model diagram (unit: m)

隧道计算参数,如表4所示.

表4 隧道计算参数Tab.4 Calculation parameters of tunnel

由表4可知，有

xi=2re(i-0.5).

(20)

di=xi+0.7.

(21)

掌子面前方开挖段地表质点A2的爆心距为

振动波的传递时间为

(23)

等效球形药包i在地表质点A2产生的振速函数为

(24)

地表振速预测结果，如表5所示.表5中：vp为预测最大振速;η为相对误差.

表5 地表振速预测结果Tab.5 Prediction results of surface vibration velocity

根据相关规定，铁路路基的振速要求控制在2 cm·s-1以内.由表5可知：预测值与实际监测值的相对误差在10%左右，实际监测最大振速和计算预测的最大振速均满足该要求.

5 结论

1) 在实际岩石介质中球形药包的地表振速函数的基础上，通过保角变换将隧道掌子面前方开挖段地表质点和爆破点映射到复平面中.将开挖段质点振动问题转化为岩石介质中的振动问题，成功建立了隧道掘进中掏槽孔爆破引起的隧道已开挖段上方地表质点的振速函数.

2) 算例中隧道埋深较浅，地层变化情况较为复杂，计算公式在推导过程中没有考虑p波在隧道顶和地表之间的叠加作用，且忽略了波在各地层交界处的折反射作用，当地质条件差异性较大，并受到地下水等的影响时，计算结果可能受影响较大.因此，计算预测值与实际监测值存在一定的偏差，但两者的相对误差在工程的允许范围之内，能够为爆破优化设计提供一定的参考.