采用局部粗糙集模型的决策规则提取

张晓萍，李伟康, 李进金,2

(1. 华侨大学 数学科学学院，福建 泉州 362021; 2. 闽南师范大学 数学与统计学院，福建 漳州 363000)

经典粗糙集理论由波兰学者Pawlak[1]首次提出,该理论可处理不确定、不精确、不一致的不完全数据信息.虽然经典粗糙集理论不需要数据的先验信息，但仍具有一定的局限性[2-3]:需建立在等价关系基础上、在大数据背景下计算效率低、属性约简的过拟合.

为满足数据处理的要求,许多学者对经典粗糙集理论进行一系列推广,如一般关系下的粗糙集、变精度粗糙集[4-5]、局部粗糙集[3]、决策理论粗糙集[6]等,变精度粗糙集是在经典粗糙集的基础上,引入参数β(0≤β<0.5),即允许一定的错误分类率发生[7-8].当β=0时,经典粗糙集就是变精度粗糙集的特例.局部粗糙集理论可以更好地应用于大数据处理,在计算上、下近似时,无需考虑论域中的所有对象,只需考虑样本中的对象,提高了数据处理的效率.文献[6]引入决策风险,作出的决策规则需使决策风险最小.目前，粗糙集理论及其推广已广泛地应用于模式识别[9-10]、知识发现[9,11-12]、规则提取[9,13]和决策管理等领域.

概念逼近与属性约简是研究粗糙集的两个关键因素[3],对给出的新样本做有效的概念逼近可以更加客观地观察新样本,通过属性约简、对象与属性值之间的关系，可以对决策信息系统进行有效的决策规则提取.决策规则提取往往出现在决策信息系统数据的处理中.利用粗糙集理论进行决策规则提取时，一般会有两类决策规则:确定性和可能性决策规则[14-16].基于此，文中对基于局部粗糙集模型下的决策规则提取进行研究.

1 基础知识

假设U是一非空有限集合,称为论域,R⊆U×U是U上一等价关系，则K=(U,R)称为近似空间.x∈U的等价类记为[x]R,若[x]R=[y]R,则称对象x与y在等价关系R上是不可区分的.

定义1[3]给出一个近似空间K=(U,R)及U的任意非空子集X,X的下近似和上近似分别为

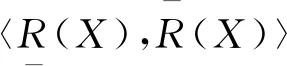
2 局部粗糙集

在数据处理过程中,为了计算给定的每个样本X的上、下近似,需要考虑给定数据集的所有对象，在大数据背景下,要花费较多的时间和精力.因此，为了提高数据处理的效率,文献[3]结合经典粗糙集和决策理论粗糙集提出局部粗糙集.

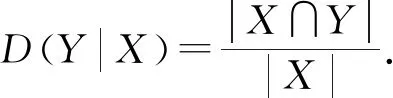
定义3[3]设(U,R)为一近似空间,R⊆U×U为U上一二元关系,D是定义2U×2U上的包容度函数,则U上的任一非空子集X的α-下近似和β-上近似分别为

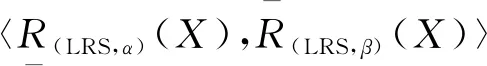
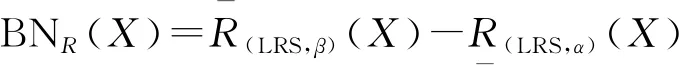
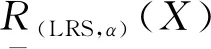
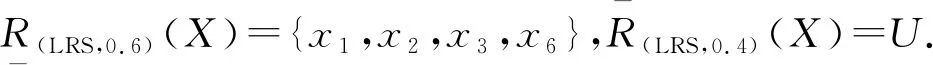
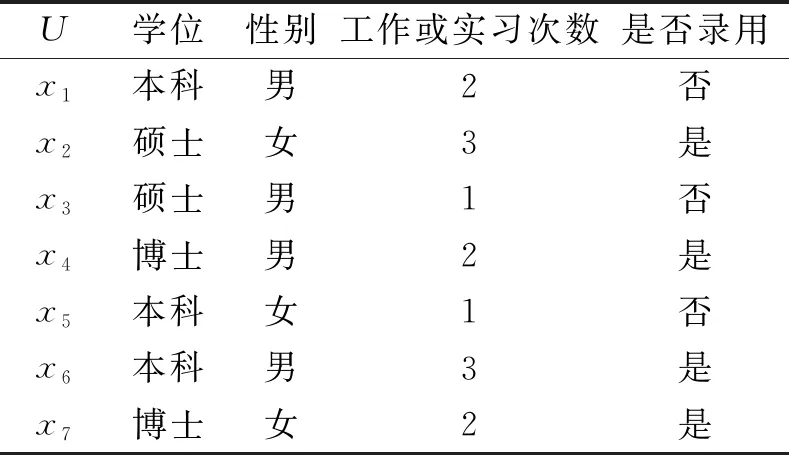
表1 某公司面试人员的基本信息表Tab.1 Basic information table of interviewers of company

由例1可知：在局部粗糙集与经典粗糙集中,给出论域的任一子集,调整参数值可使子集的上、下近似更加接近该子集,即应用局部粗糙集理论可以对集合做更有效的概念逼近,数据处理更加精确.

3 局部粗糙集模型中的决策规则提取

3.1 规则提取[14]

用∧与∨分别表示逻辑连接词“和”与“或”.在决策信息系统S=(U,C∪{d})中，C为条件属性，d为决策属性.任何属性值对(a,v)称为A原子，a∈A⊆C,v∈Va,Va为对象在属性a下的取值．任何A原子或者不同的A原子的∧称为A描述．若t是A描述，则出现在t中的属性记为A(t)，A(t)={a|(a,v)∈t}，具有描述t的对象集称为t的支持，用‖t‖表示，‖t‖={x∈U|a(x)=v,∀(a,v)∈t}，则易得‖t∩s‖=‖t‖∩‖s‖,‖t∪s‖=‖t‖∪‖s‖.

对于A⊆C，记DES(A)={t|t是一个A描述且‖t‖≠∅}，若对任何的t∈DES(A)，有A(t)=A，则称t是一个满的A描述，记FDES(A)={t|t∈DES(A)且A(t)=A}.

例2继例1，取A={学位,性别},t1=(学位,本科)，则‖t‖={x1,x5,x6}，此时，A(t)={学位},A(t)≠A，故t1不是满的A描述；取t2=(学位,本科)∧(性别,男)，则‖t2‖={x1,x6}，此时，A(t2)={学位,性别},A(t2)=A，则t2是一个满的A描述．

以下讨论都建立在t是一个满的A描述的基础上，即t∈FDES(A)．

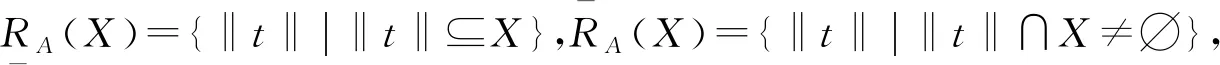
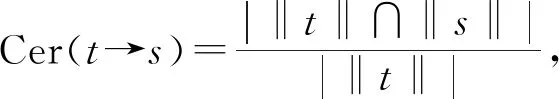
3.2 局部粗糙集的决策规则提取

在每个决策信息系统S=(U,C∪{d})中都可以产生决策规则,合理的决策规则对新样本的决策具有重要的参考作用,这不仅要求数据具有真实性和有效性,也要求在分析数据时提取合理的决策规则.

定理1对于决策信息系统S=(U,C∪{d}),s=(d,w)，w∈Vd，t∈FDES(C)，且0≤β<α≤1，则

1)D(‖s‖|‖t‖)≥α，当且仅当|{x∈U|d(x)=w∈∂(t),∀a∈C,(a,a(x))∈t}|≥α|‖t‖|;

2)D(‖s‖|‖t‖)>β，当且仅当|{x∈U|d(x)=w∈∂(t),∀a∈C,(a,a(x))∈t}|>β|‖t‖|.

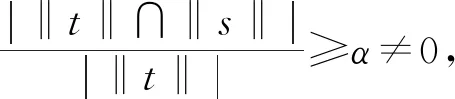
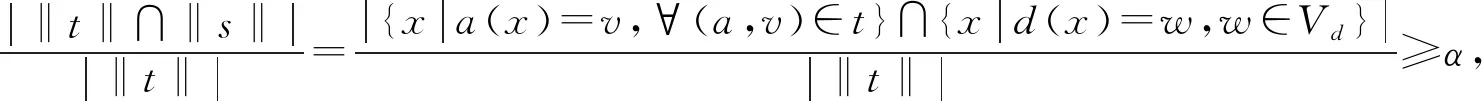
|{x∈U|d(x)=w∈∂(t),∀a∈C,(a,a(x))∈t}|≥α|‖t‖|.

“⟸”充分性.w∈∂(t)={d(x)|x∈‖t‖},则‖t‖∩‖s‖≠∅,即D(‖s‖|‖t‖)>0.又因为

|{x∈U|d(x)=w∈∂(t),∀a∈C,(a,a(x))∈t}|≥α|‖t‖|，

2) 当0<β时,证明同1).

当β=0时,D(‖s‖|‖t‖)>0，当且仅当|{x∈U|d(x)=w∈∂(t),∀a∈C,(a,a(x))∈t}|>0.

“⟹”必要性.当D(‖s‖|‖t‖)>0时,‖t‖∩‖s‖≠∅,存在x∈‖t‖∩‖s‖,使d(x)=w,故w∈∂(t)={d(x)|x∈‖t‖}.同时，有{x∈U|d(x)=w∈∂(t),∀a∈C,(a,a(x))∈t}≠∅.

“⟸”充分性显然可见.

证毕.

定理2决策信息系统S=(U,C∪{d})中,s=(d,w)，w∈Vd，t∈FDES(C)，且0≤β<α≤1，则

证明：由定理1即可证明.

对于X⊆U,A⊆C,基于局部粗糙集模型，推广可得

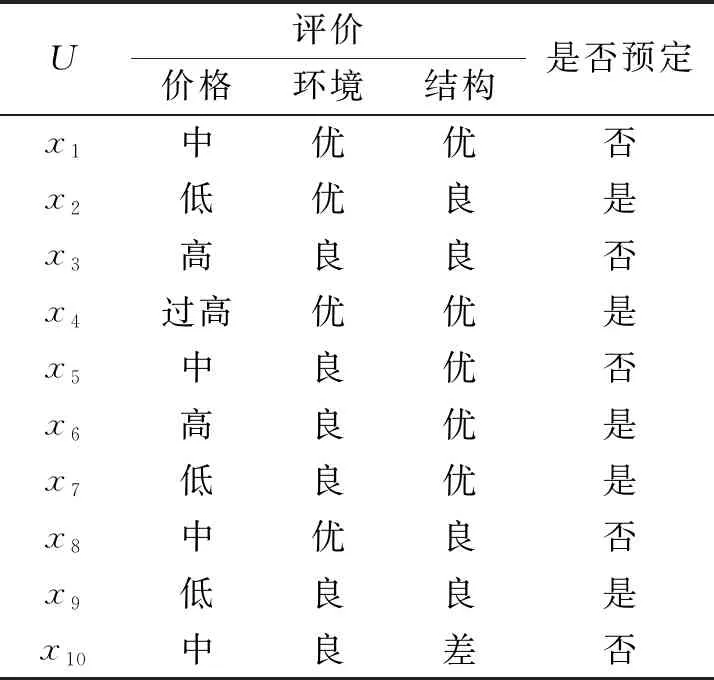
表2 某同学浏览的房子的基本信息表Tab.2 Basic information table of house browsed by student

例3某同学去旅游前打算预定房子,他查看了10间房子,依次标记为x1～x10,并且将价格、环境、结构作为评价指标,即属性集C={价格,环境,结构}.该同学将此次浏览的信息制成表格,并给出“是否预定”的初步决策,如表2所示.

取α=0.6,s=(是否预定,是),则‖s‖={x2,x4,x6,x7,x9},能够做α-确定的决策情况如下.

1) 考虑A=C={价格,环境,结构}，有t=(价格,低)∧(环境,优)∧(结构,良)，决策t→s的确定性因子Cer(t→s)=1；t=(价格,过高)∧(环境,优)∧(结构,优)，决策t→s的确定性因子Cer(t→s)=1；t=(价格,高)∧(环境,良)∧(结构,优)，决策t→s的确定性因子Cer(t→s)=1；t=(价格,低)∧(环境,良)∧(结构,优)，决策t→s的确定性因子Cer(t→s)=1；t=(价格,低)∧(环境,良)∧(结构,良)，决策t→s的确定性因子Cer(t→s)=1.

2) 考虑A⊆C={价格,环境}或者{环境,结构}或者{价格,结构}，那么，有t=(价格,低)∧(环境,优)，决策t→s的确定性因子Cer(t→s)=1；t=(价格,过高)∧(环境,优)，决策t→s的确定性因子Cer(t→s)=1；t=(价格,低)∧(环境,良)，决策t→s的确定性因子Cer(t→s)=1；t=(环境,良)∧(结构,优)，决策t→s的确定性因子Cer(t→s)=0.67；t=(价格,过高)∧(结构,优)，决策t→s的确定性因子Cer(t→s)=1；t=(价格,低)∧(结构,良)，决策t→s的确定性因子Cer(t→s)=1；t=(价格,高)∧(结构,优)，决策t→s的确定性因子Cer(t→s)=1；t=(价格,低)∧(结构,优)，决策t→s的确定性因子Cer(t→s)=1.

3) 考虑A⊆C={价格}或者{环境}或者{结构}，那么，有t=(价格,低)，决策t→s的确定性因子Cer(t→s)=1；t=(价格,过高)，决策t→s的确定性因子Cer(t→s)=1；t=(结构,优)，决策t→s的确定性因子Cer(t→s)=0.6.

4 结束语

在经典粗糙集模型的决策规则提取中,确定因子Cer(t→s)=1的规则称为确定性规则,结合局部粗糙集模型给出的规则提取公式，引入参数值α,α∈(0,1],使规则提取公式的泛化能力更强,适用性更广.当α=1时，即普通的决策规则提取情况.在今后的工作中,将进一步比较局部粗糙集模型与其他粗糙集模型的决策规则,以及多个粗糙集模型的结合决策规则提取.