一种改进的高维孤立点挖掘入侵检测方法

申利民，孙中魁，2，陈 磊，冯佳音，李志明

1(燕山大学 信息科学与工程学院，河北 秦皇岛 066004) 2(华北理工大学轻工学院 电气信息学院，河北 唐山 063000) 3(华北理工大学 研究生院，河北 唐山 063000)

1 引 言

随着现代信息技术的发展，赛博空间安全问题的重要性也随之凸显出来.2019 年全年超过 6，200 万个计算机恶意程序样本被捕获，日均传播次数达 824 万余次，涉及计算机恶意程序家族 66 万余个(1)https：//www.cert.org.cn/ publish/main /upload /File/2019-year.pdf.截止2019年12月，CNCERT接收到网络安全事件报告107801件，较2018年底增长1.0%(2)http：//www.cac.gov.cn.为了适应日趋复杂化、多样化的网络环境和各种各样的网络入侵手段，入侵检测系统(Intrusion Detection System，IDS)通过分析网络连接和系统审计数据，生成安全策略并发现入侵攻击，已经成为赛博空间安全不可或缺的组成部分.

在现实网络中，入侵检测系统面对的数据大都是高维数据，部分研究者们对高维数据首先采用特征提取或特征选择的方法降低数据维度，再采用传统的数据挖掘方法进行处理.Tian等提出了一种基于PCA的分层孤立点检测模型，首先基于PCA进行特征提取，然后利用正常数据建立一个异常检测模型，再分析异常数据类型[1]；Zyad等在PCA的基础上提出了利用修剪后的平均向量来估计平均向量，从而使Trimmed PCA具有更好的鲁棒性[2].降维的方法可以剔除某些特征，降低计算的时间复杂度，但每个特征代表不同的孤立值，如果错误的选择特征就会得到错误的孤立值，从而产生不适合未来计算的近似结果.基于低维数据的挖掘算法在面对高复杂性、稀疏性和多样性的高维数据时往往无能为力，适用于低维数据的数据挖掘算法在处理高维数据时通常会遇到算法效率降低，存在传统的基于距离和密度的定义失效等问题，降低了入侵检测准确性[3].研究者们提出了针对高维数据的入侵检测方法.Zhang等针对高维数据网络数据流中的异常检测，提出了SPOT技术，具有良好的检测效果[4]；Prajapati等针对高维数据中的数据不均匀和刚性聚类问题，利用K-mean算法和模糊C-Mean(FCM)算法的优点，提出了一种最近邻搜索算法，能在更短的时间内实现最近邻搜索[5].

入侵行为中的“攻击”数据通常被视为异常数据，而孤立点数据挖掘是对大规模数据中偏离正常行为的异常数据进行的挖掘，因此孤立点数据挖掘对入侵行为分析具有重要意义.针对高维孤立点挖掘，研究者提出了几种典型的孤立点挖掘算法：基于空间投影[6，7]、基于超图模型[8，9]和基于频繁模式的算法.基于频繁模式的孤立点挖掘算法简单、易于理解，并且比前两种算法，有着更低的时间复杂度，研究者做了广泛的研究.早期，He等提出了频繁模式孤立因子(FPOF)的度量概念，并提出了基于频繁模式的孤立点挖掘算法(FindFPOF)，通过计算每条数据的频繁模式因子来发现孤立点[10]；周等在FindFPOF的基础上提出了加权频繁模式孤立因子的概念，并在此基础上给出一种快速数据流孤立点检测算法，该算法具有良好的适用性和有效性[11]；王等提出了一种新的算法NFPOF(New Frequent Pattern Outlier Factor)，通过频繁模式的相关属性进一步精确定位每一条孤立点数据的异常属性[12]；Yuan等针对权值严重影响孤立值检测结果的问题，提出了一种加权频繁模式孤立点挖掘方法(WFP-Outlier)，用于从加权数据流中发现隐式孤立点[13].

综上所述，基于频繁模式的高维孤立点挖掘在入侵检测中具有非常重要作用，但在基于频繁模式算法及其改进算法中存在两个问题，首先上述算法需要获取完全频繁模式，但是在高维数据中，发现频繁模式的完全集是非常困难的；其次频繁模式的挖掘算法的时间复杂度与频繁模式的数量有直接关系，频繁模式的数量越多，时间复杂度越大.针对基于频繁模式的高维孤立点挖掘算法中存在的不容易获取完全频繁模式和时间复杂度高等问题，引入关联规则中的最大频繁模式因子的概念，提出一种基于最大频繁模式因子的高维孤立点挖掘(MFPOF-OM)算法，并把其和入侵检测结合起来，在保证检测性能优良的前提下，降低了时间复杂度.

2 基于最大频繁模式因子的高维孤立点挖掘生成入侵检测模式

设D={tl，t2，…，tn}为一个包含n个网络行为记录t的数据集，tk称为事务.I={il，i2，…，ip}是网络行为记录中所有属性的集合，im称为项目.

定义1.项目集：I的任何子集X称为D的项目集.

定义2.支持度：项目集X的支持度记为support(X)：

(1)

其中：‖D‖表示数据集D的事务总数，‖X‖表示项目集X的支持数.

定义3.频繁模式：如果项目集X的支持度support(X)≥MinSP，则X为频繁模式，否则称为非频繁模式，其中MinSP表示用户定义的最小支持度.

定义4.超集：若一个集合S2中的每一个元素都在集合S1中，且集合S1中可能包含S2中没有的元素，则集合S1就是S2的一个超集.S1是S2的超集，则S2是S1的真子集，反之亦然.

定义5.最大频繁项模式：频繁项集X，如果其所有超集都是非频繁项集，那么称X为最大频繁模式.

定理1.设X、Y是数据集D中的项集，如果X⊆Y，若Y是频集，则X也是频集.

设Y为最大频繁模式，由定义5可知Y必为频繁模式，如果X⊆Y成立，则有定理1可知，X必为频繁模式，也即是最大频繁模式中已经包含了所有的频繁模式.

由以上分析可知，基于最大频繁模式的孤立点挖掘算法中只需要发现最大频繁模式集，而不是完全频繁模式集，既解决了发现频繁模式的完全集的困难问题，又因为最大频繁模式的数量远远小于频繁模式的数量，从而可以降低算法的时间复杂度.

2.1 数据离散化

入侵检测的数据类型可分为文本型数据、离散数值型数据和连续数值型数据3大类，而最大频繁模式的挖掘要求数据类型必须是离散数值型，因此需要对连续数值型数据进行离散化处理，转化成为可靠的精确的适合进行高维孤立点挖掘的数据.

连续数据的离散化就是将连续数据分割为有限个相互独立的区间.离散化的方法有多种，其中基于聚类分析的方法因其可以根据数据的分布特点自行决定属性值如何划分区间，能够尽量减少人工的干预，在实际中得到广泛的应用.聚类形成模式类之后，同一个模式类内的对象因其高度相似可当成一个对象来对待，而不同模式类的对象因其迥异性而被看作不同的离散值.

基于聚类分析的离散化方法有两个步骤：

1)对连续数据类型的属性值进行聚类.

2)聚类后，同一个模式类所包含的连续属性值作为一个对象，统一标记，而不同模式类的数值分别标记，完成离散化处理.

其中，基于聚类分析离散化的关键步骤是是对属性值的聚类挖掘.

K-means算法作为一种基于划分的无监督的经典算法，在实践应用被广泛应用，但K-means算法也有其本身的缺点，就是对聚类个数K和初始聚类中心的选择非常敏感.

针对K值敏感的问题.因为在离散化过程中K值并不是固定和唯一的，所以可采用手肘法确定最优的K值.手肘法的核心思想是：当K小于最优聚类数时，增大K值会大幅增加每个模式类的聚合程度，聚合程度的好坏由样本的聚类误差平方和(SSE)来表示，SSE会大幅下降，当K达到合理数量的模式类时，SSE将急剧下降，最后，SSE值趋于平坦，即SSE和K之间的函数关系呈肘形，并且对应于肘部的K值是最佳的簇数.

误差平方和(SSE)定义为：

(2)

其中，Ci为第i个簇，p为Ci中的样本点，mi为Ci的质心(Ci中所有样本的均值).

针对初始聚类中心的选择敏感的问题，采用最大距离法选取K个样本作为初始中心点.最大距离法的核心思想是认为所有样本中距离最远的样本点最不可能被分到同一个模式类中.

3https：//www.unb.ca /cic/datasets/index.html

2.2 基于最大频繁模式因子的高维孤立点挖掘算法思想

基于FindFPOF算法中频繁模式因子(FPOF)的概念，提出最大频繁模式因子(MFPOF)的定义.

定义6.最大频繁模式因子：对于数据集中D中的每个网络行为记录t，MFPOF(t)定义为：

(3)

其中：

MFPs(D，MinSP)表示满足给定最小支持度阈值MinSP的数据集D的最大频繁模式集合；

‖MFPs(D，MinSP)‖表示最大频繁模式集合中最大频繁项的个数；

support(X)表示一个最大频繁模式X的支持度.

基于最大频繁模式因子的高维孤立点挖掘(MFPOF-OM)算法描述如算法1所示.

算法1.MFPOF-OM算法

输入：D//网络行为数据集

MinSP//最小支持度阈值

k//孤立点个数阈值

输出：k个网络行为孤立点数据记录

Begin：

//基于PF-Tree挖掘出最大频繁模式集合

1.对于D，生成满足MinSP的项头表HeaderTable(D)；

2.对于D，采用PF-Tree算法生成满足MinSP的频繁项树，记为：T；

3.采用一种改进的高效最大频繁模式因子挖掘算法，获取MFPs(D，MinSP)和support(X)；

//基于生产的最大频繁模式，开始孤立点挖掘

4.foreachtinD

5.依据公式(3)，计算每个记录t的最大频繁模式因子值：MFPOF(t)；

6.end foreach

7.获取所有t的MFPOF值；

8.对所有t，按照MFPOF值升序排序；

9.return MFPOF值最小的前k网络行为记录，即k个网络行为孤立点数据

End

MFPOF-OM算法分3个部分：1)从数据库中挖掘最大频繁模式；2)计算每个网络行为记录的MFPOF(t)；3)发现k个孤立点数据.总的时间复杂度为O(n2+n*l+n*logn)，其中n表示数据量的个数，l表示最大频繁模式的个数.

2.3 基于关联分析自动构建误用检测模式

采用关联分析可以自动发现网络行为的数据特征，关联分析产生的最大频繁模式能够反映网络行为数据的最大共同特征，最大共同特征又是通过网络行为数据的属性值表示出来的，可利用这些属性值来构建具有很强分类能力的入侵检测模式[14].

以MFPOF-OM算法所获取的孤立点数据集作为输入，并设定一个最小支持度阈值，算法可参考算法1的1-3步，可以获取孤立点集的最大频繁模式，即为网络攻击的入侵检测模式.

3 实验分析

为了对所提出的方法进行验证，本文使用NSL-KDD数据集3作为实验数据，该数据集包含了12多万条连接记录，每条连接记录包含41个表示连接记录特征的条件属性和1个表示连接记录攻击类型的决策属性.其中第20个属性(num_outbound_files)的属性值全为0，依据信息论理论，信息熵为0，因此剔除第20个属性.

NSL-KDD的训练数据集包含24种攻击类型分类标识，所有的分类标识都可以根据其攻击特点映射为4种攻击类别：Probing、DoS、U2R和 R2L，及一种正常类别：Normal，共5大类.

所有的实验在MATLAB 2012中实现，对4组样本数据Normal+DoS，Normal+Probing，Normal+R2L，Normal+U2R从准确度和复杂度两个方面进行分析.

3.1 准确度分析

4组样本数据分析获取的DoS、Probing、R2L、U2R入侵检测模式实验结果如图1所示.对4种攻击的入侵检测模式进行综合分析，并以检测率(DR)和误报率(FPR)作为判定入侵检测模式的性能评价标准.

检测率、误报率分别定义为：

检测率=(检测出的异常攻击数/异常攻击总数)*100%

误报率=(错误分类的进程总数/正常的进程总数)*100%

1)4种网络攻击模式测试结果分析

通过比较4种网络攻击在不同MinSP阈值情况下的检测率和误报率，来说明所提算法的检测效果，进而验证所提算法的可行性.入侵检测攻击模式由一条或多条规则组成：每条规则内部各属性是“与”的逻辑关系，即所有的属性取值都满足要求则本条规则成立；规则之间是“或”的逻辑关系，即多条规则只要其中一条成立则可判定本条记录为一个网络攻击行为.

实验结果从检测率、误报率两个性能指标来综合衡量入侵检测模式的检测效果.以Probing攻击入侵检测模式为例进行数据分析.实验过程中MinSP所取阈值不同，则获取的入侵检测模式也不同，实验结果如图1(b)所示.图1(b)表示MinSP分别为58000和59000两个阈值下获取的入侵检测模式，并用获取的Probing入侵检测模式分别对5种数据类型(即DoS、Probing、R2L、U2R 4种攻击数据和Normal类型)进行检测.分析发现，在阈值为59000的情况下，Probing入侵检测模式对Probing数据的检测率为95%，但是用Probing入侵检测模式来检测其它类型数据会存在一定误差，如检测Normal数据，会把3%的Normal数据误检测为Probing类型数据，对DoS数据误检率为2%，对R2L数据误检率为1%，对U2R数据误检率为10%.阈值为58000时各检测结果如图1(b)中白色柱体所示，不再一一描述.通过对多个阈值下的检测结果综合分析，阈值为59000时的检测结果最好，因此把阈值为59000时的入侵检测模式作为Probing攻击的入侵检测模式，模式规则如表1所示.

比较图1中的4种攻击入侵检测模式发现，当最小支持度阈值较大时都会有更好的检测率，对其它类型数据的检测误差则大小变化不一，但基本持平.这正是孤立点挖掘的特点决定的，阈值越大孤立点的个数越少，更能反映攻击类型数据的特征.当然阈值也有一定的限定，如果阈值取值过大反而会对降低检测率造成不良影响.

表1 阈值等于59000时Probing攻击的入侵检测模式Table 1 Misuse detection patterns of Probing attack when the threshold is 59000

比较图1中的4个子图发现U2R类型数据在DoS、Probing和R2L攻击入侵检测模式中都有较高的检测误差，分别为4%、10%和33%；U2R攻击入侵检测模式的检测率相较于其它3种攻击入侵检测模式，它的检测率也相对不高，只有87%的检测率.这是由NSL-KDD数据集中U2R类型数据的特点决定的，U2R的数据量太少，只有52条，以至于数据挖掘无法充分发现其数据特征，导致检测性能不尽完善.

图1 4种网络攻击模式的测试结果Fig.1 Test results of four network attacks

比较图1(c)和图1(d)发现，利用R2L攻击入侵检测模型检测U2R数据和利用U2R攻击入侵检测模型检测R2L数据都有较高的误差，这说明R2L类型数据和U2R类型数据之间相较于其他3种类型数据，具有较高的数据相似性，这与现实中2种网络攻击的特点相符.

2)基于高维数据下入侵检测结果对比分析

为了测试所提算法的准确度，把所提MFPOF-OM算法与FindFPOF算法[10]、NFPOF算法[12]、AOD-FP-MaxFPOF算法[15]、ADASYN-SDA算法[16]进行比较，其中FindFPOF、NFPOF、AOD-FP-MaxFPOF是3种基于频繁模式或改进的基于频繁模式孤立点检测算法，ADASYN-SDA是基于深度学习的算法，比较结果如图2所示.结果表明MFPOF-OM算法优于FindFPOF和NFPOF算法；和AOD-FP-MaxFPOF算法比较，检测率上非常接近，误报率比后者相比偏高；和基于深度学习的ADASYN-SDA算法相比，两个性能指标都稍有不如，但ADASYN-SDA算法需要复杂的前期数据处理，首先需要使用ADASYN算法进行数据过采样处理，然后使用Adam优化算法，以及Dropout正则化对SDA深度学习模型进行改进，提取出低维的集成特征，最后再在Softmax分类器中进行入侵检测识别，会大大增加算法的时间复杂度.从总体性能上分析显示，所提算法和有监督的深度学习方式相比性能稍有不如，但在无监督的检测算法中性能表现较佳，网络中的入侵行为能够被有效地检测出来，可以满足实际的运行需求.

图2 其它入侵检测方法和所提方法的比较Fig.2 Comparison between other intrusion detection methods and the method proposed

3)高维入侵检测和降维入侵检测的对比分析

入侵检测系统中的数据是高维的，高维数据表达能力较强，能够刻画入侵检测系统内部复杂的结构.但在入侵检测分析中，很多方法都使用了降维的概念，进行维度的约简.而某些看似不重要的维度，特别是在孤立点挖掘算法中，更可能代表着有用的信息，而这些维度的消除，可能会影响到入侵检测结果准确度.且原始数据处理过程中的降维也会增加入侵检测的时间复杂度.为了比较高维数据入侵检测和数据降维入侵检测对检测性能的影响，利用MFPOF-OM算法和两种基于降维的方法基于PCA的特征提取[1]、截断均值LDA方法[17]进行对比分析，结果如图3所示.从中可以看出，MFPOF-OM算法和文献[1]中检测性能基本一致，而又明显的优于文献[17]所提出的方法，说明不适当的数据降维方法会把某些含有重要孤立点信息的特征剔除掉，从而大大降低入侵系统的检测性能.

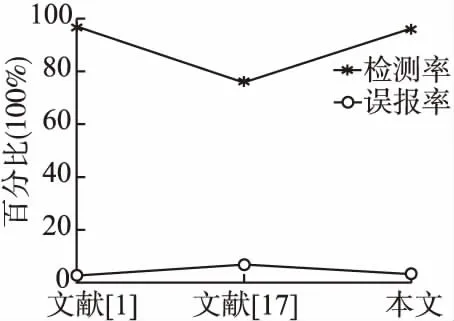
图3 降维挖掘和高维挖掘测试比较Fig.3 Comparison dimension reduction methods with the method proposed in this paper

3.2 时间复杂度分析

对4组样本数据Normal+DoS、Normal+Probing、Normal+R2L、Normal+U2R进行复杂度分析.FindFPOF、NFPOF、AOD-FP-MaxFPOF这3种基于频繁模式及其改进算法的流程类似，都可以分为3步，其中第1步从数据库中挖掘频繁模式和第3步发现k个网络行为孤立点数据，这两步基本雷同，只有第2步因为算法重点不同而不太一样.FindFPOF算法第2步是计算每个网络行为记录的FPOF(t)；NFPOF算法是计算新频繁模式离群因子NFPOF(t)；AOD-FP-MaxFPOF算法是计算最大频繁孤立点因子MaxFPOF(t).依据所给算法分析，时间复杂度也可根据算法流程分为3部分，且3种算法的时间复杂度基本一致，总的时间复杂度为O(n2+n*m+n*logn)，其中n表示数据量的多少，m表示频繁模式的多少.

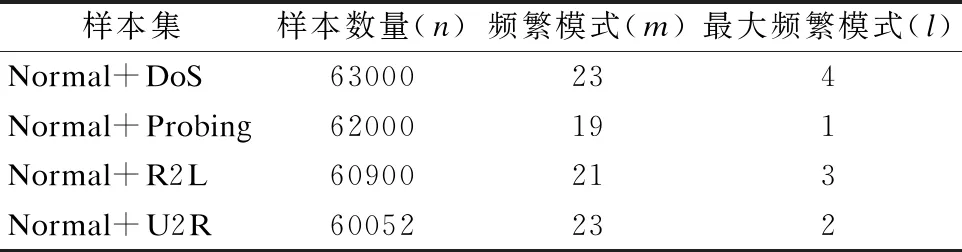
表2 两类挖掘算法结果比较Table 2 Compared the results of two mining algorithm

与上述算法一样，MFPOF-OM算法流程图也分3步，如2.2节中所述，总的时间复杂度为O(n2+n*l+n*logn)，其中m表示数据量的个数，l表示最大频繁模式的个数.对于海量数据来说，n取值足够大，两种算法的时间复杂度从理论计算上都可以简化为O(n2).但在实际运行中，当n取值一定时，会因为l≪m，4组样本数据获取的频繁模式个数(m)和MFPOF-OM算法中的最大频繁模式个数(l)如表2所示，从而使MFPOF-OM算法比上述3种算法具有更优的时间复杂度.

4 结 论

针对现实中入侵检测系统中多为高维数据这一现实问题，利用基于频繁模式高维孤立点挖掘的相关技术，本文提出了一种基于最大频繁模式因子的高维孤立点挖掘算法(MFPOF-OM).MFPOF-OM算法只需挖掘出最大频繁模式集，解决了基于频繁模式孤立点算法中挖掘完全频繁模式比较困难的问题，也因频繁模式的数量的大幅减少，从而降低算法的时间复杂度.实验表明，所提出的方法是可行的，相较于对比算法，在保证了检测性能优良的前提下，进一步降低了时间复杂度.