改进Rossler方程的异变混沌堆混合加解密系统
2020-12-09林之博刘媛华
林之博,刘媛华
(上海理工大学 管理学院,上海 200093)
1 引 言
数据加密是通讯信息安全中必不可少的环节.最常用的非对称加密算法之一RSA算法安全性极高,根据公钥或私钥无法逆推与之配对的密钥序列,使得加密后的密文难以被暴力破解[1,2].但由于RSA等算法复杂度高,对于大型文件,难以在短时间内实现加密或解密,故国际上常用的信息加密标准一般基于非对称加密算法与对称加密算法的混合使用[3].
对称算法是指通信两端使用相同密钥进行加密解密的算法.常见的对称算法有DES算法、AES算法等,具有复杂度不高,加密时间短,在密钥未知的情况下难以暴力破解的特性.但DES算法作用长度短,密钥安全性在特定情况下容易变为弱密钥或半弱密钥被破解,且采用的混淆加扩散协议不能对抗差分和线性密码分析[3];而AES加密则存在不能完全隐藏明文模式、加密图片后可以看到轮廓,且加密后文件大小翻倍的缺点[3].目前国内外进行了不少关于对称加密算法优化的研究,有学者通过结合混沌系统和AES算法来加强AES算法对图像加密的性能[4],该方案可以显著增强AES作用于图片时像素点轮廓模糊化程度;另有用PIC微控制器通过Zigbee信道对图像加密[5],改进混沌映射随机性增强图像加密的非线性特性;以及使用超混沌映射[6]、双logistic混沌[7]等对数字图像进行加密,在小规模图像加密上具有优势,且已经证明任意混沌加密可以有效对抗差分、线性密码分析[8-10],但使用的混沌系统密钥空间有限[6,8,9],都低于2256组.上述研究一定程度上都增加了对称加密复杂性,对于大型文件如视频、可执行程序等的加密耗时较长.
因此,考虑基于混沌系统理论,设计一种改进的混沌信号序列与任意文件进行叠加的加解密通信方案,用新算法替换原有混合加密中的对称算法,尽可能实现占用较少资源与时间,对任意格式的文件进行混合加密解密,简化文件加密解密计算的流程,使明文信息完全不可见,并保证混沌加密的抗破解能力与抗传输干扰失真能力.
2 相关技术理论
RSA非对称加密算法是由Ron Rivest、Adi Shamir和Leonard Adleman于1978年提出,该算法被广泛应用于公开密钥加密与电子商业中[11].RSA可以同时被应用于加密和数字签名,安全性与可靠性很高,被称为地球上最安全的加密算法之一.RSA算法加密原理是对明文的e次方除以n后求余数,其中e与n是经过严格计算后得出的.非对称加密能产生相互成对的公钥和私钥,记为(e,n)和d,用户对外可以公布(e,n),使他人获得(e,n)后,使用(e,n)进行数据加密[1,11].加密后的数据必须使用对应d进行解密,否则不能被还原为明文.由于RSA算法计算产生的密钥序列位数可以达到1024位,因此想要依靠暴力破解算出与公钥配对的私钥将需要消耗数十万年的时间.但由于RSA过于复杂,常被用于加密较短的信息,不适用于加密大规模数据[11].
混合加密是指,用户之间首先交换通过非对称算法产生的公钥(ek,nk),并保留对应私钥,且私钥dk需严格保护,不得泄露.在数据通信之前,用户之间通过对方公钥加密一个对称的密钥,并将加密后的对称密钥发送给通信对象[1,11].通信对象接受后,使用私钥解密,获取对称密钥.接下来,使用任意对称加密算法对任意大小的数据进行加密发送.该过程可描述为:
KeyE=KeyeMODn
(1)
Key=KeyEdkMODn
(2)
MessageE=Key(Message)
(3)
Message=Key(MessageE)
(4)
混合加密的优点在于:结合了非对称与对称加密算法的优势,摒弃了二者的缺陷.由于对称密钥通常规模较小,非常适合用RSA进行加密,而对称加密算法适用于加密大型数据.通过使用混合加密技术,不但能在较短时间完成加密解密,还可以同时保证密文安全性、可靠性[11].
Rossler方程组是Otto Rossler于1976年发现和提出的经典混沌系统[12],用微分方程组可表示为:
x′=-(y+z)
(5)
y′=x+ay
(6)
z′=b+z·(x-c)
(7)
其中x′、y′、z′分别为状态参量,a、b、c为控制参量.Rossler方程组是简单系统,但该系统存在著名的混沌行为,最经典的一例分别取a=0.2、b=0.2、c∈[2,4.2]时,系统产生混沌吸引子,分别出现平衡态、周期2、周期4、周期8、混沌现象[12,13];且系统相空间中可见平均周期振荡成分,自相关函数几乎重合[12-14].Rossler混沌在电子通信加密、模拟电路、尤其是图像复合加密等领域常有应用.
Rossler混沌序列具有很明显的特异性和模式特征.一般取3个控制参量作为密钥设计加密算法,参量越长,密钥越多.在数据仿真实验中,Rossler在不同的相空间位置上表现出完全不同的空间形态,且经Anylogic构造系统动力学模型演算得到如表1所列举的结果,可知每一类形态对应的样本方差都有较大差异.因此Rossler混沌很适合用于产生原始混沌信号序列.

表1 Rossler混沌系数与对应形态举例Table 1 Examples of Rossler′s chaos coefficient and corresponding forms
3 算法设计与应用
3.1 改进Rossler混沌模型
通过分析加密结果中的Rossler序列数理特征,可以大致确定混沌的形态和参数取值的范围,这很不利于数据加密的安全性.因此考虑改进原Rossler系统,实现在保留Rossler混沌空间状态转移特性的基础上,增加混沌信号序列的混乱度和随机性.故基于Rossler方程组改进设计新的系统模型,见式(8)-式(16):
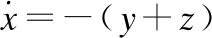
(8)
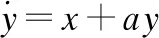
(9)

(10)
(11)
(12)
(13)
Xsn+1=[Xn-(Yn+Zn)·Δs]·IMODGear
(14)
Ysn+1=[Yn+(Xn+aYn)·Δs]·IMODGear
(15)
Zsn+1={Zn+[b+Zn(Xn-c)]·Δs}·IMODGear
(16)
其中I为信号放大控制参量,Gear用于调控序列模式.假设∀e∈{Xsn+1,Ysn+1,Zsn+1}有Signal=e×I,当∃I1,I2,且lgI1>lgI2时,根据Rossler混沌信号特性可知在I1和I2放大下式(17)一定成立:
(17)
即I1处理后的信号一定比I2处理后的信号具有更高的混乱程度.取状态参量x、y、z与控制参量a、b、c作为加密密钥矩阵组分.特别地,简称系统产生的3个新混沌序列式(14)-式(16),在空间中展现出的立体形态为“异变混沌堆”.
3.2 环链序列置换子算法
结合异变混沌堆,针对文献[8]中的二进制明文循环移位加密算法进行变形和泛化,设计一套多维度数据加解密子算法.新算法可指定循环置换范围且具备普适性,具有较高运算速度和较低的空间占用.使用新算法优化原算法只适用于一维明文加密、无法直接应用于多维数据加密的局限性,并扩大系统的服务面以支持多国文字、图像和任意数据流的加密.
首先,构造一种元素连续的环链式数据结构如图1所示.

图1 环链序列结构Fig.1 Sequence structure of circle chain
存在指定的起点Start和终点End,起点与终点相连,构成环链,使得终点后移一位得到起点.设Om为原数据,Cm为加密后数据,em为混沌序列中m位上的信号.设计环链序列置换子算法.可推导出环链序列置换法则,见式(18)、式(19):
(18)
(19)
对于文字加密解密过程,将Gear置为100.先将明文转换为Unicode编码以扩大文字加密的范围.设em为选定混沌轴序列中m位上的信号,Om为对应明文Unicode序列m位上的字符ASCII码,构造一个有效ASCII码环链序列起点为32,终点为126,使用式(18)、式(19)计算字符叠加和解调信号结果.
对于图片加密解密过程,将Gear置为1000.获取图片中像素点,并计算每个像素点的RGB值,视RGB数据为三维数据,取值范围为[0,255].将3个混沌序列轴X、Y、Z的信号序列分别叠加到R、G、B上,再写回到图片中.使用式(18)、式(19)计算叠加和解调信号后的RGB值,可得加解密后的图片.
对于任意文件的加密解密,将Gear置为1000.原理与文本加密类似,根据文件读取的字节流每次产生1024位的混沌堆序列,并将读取到的文件字节流和若干组序列分别组成矩阵,见式(20)、式(21):
(20)
(21)
则对文件的加密解密过程可看作对Bytefile和Efile同一行列上的元素作为式(18)、式(19)所示的运算,其中每一个字节转换为int型取值范围为[-128,127].
对文字、图像进行加密与解密信号叠加和解调算法分别如算法1、算法2所示.
算法1.
输入:密钥序列K,文字、图像或文件数据
输出:加密后文字、图像或文件
1.初始化数据读写器FR、FW,数组E与指针P;定义K(n,m)为密钥 K产生的n到m位的序列
2.WHILEFR⊂DataDO
3.E←K(0+1024×P,1024+1024×P)
4.FOReachOinFRDO
5.C[O]←C(O,E[O])//基于公式(18)
6.ENDFOR
7.FW←C
8.P←P+1
9.FR←Data[0+1024×P,1024+1024×P]
10.ENDWHILE
11.关闭读写器
算法 2.
输入:密钥序列K,待解密文字、图像或文件数据
输出:解密后文字、图像或文件
1.初始化数据读写器FR、FW,数组E与指针P;定义K(n,m)为密钥 K产生的n到m位的序列
2.WHILEFR⊂CryptoDO
3.E←K(0+1024×P,1024+1024×P)
4.FOReachCinFRDO
5.O[C]←O(C,E[C])//基于公式(19)
6.ENDFOR
7.FW←O
8.P←P+1
9.FR←Crypto[0+1024×P,1024+1024×P]
10.ENDWHILE
11.关闭读写器

3.3 系统实现
综合3.2设计的算法与异变混沌堆模型,设计加解密软件系统.软件遵从混合加密协议,每一对用户首先需通过RSA算法建立加密通讯,再通过RSA约定混沌堆通信“频道”,经混沌堆“频道”加密通信内容,包括任意文件和文字.具体流程如图2所示.

图2 混沌堆通信加密软件操作流程Fig.2 Operation flow of chaotic stackcommunication encryption software
基于上述算法和方案,在java中编程实现软件系统,系统产生的原混沌与对应异变混沌堆空间图像举例如图3所示.图像的加密解密若使用Java ImageIO.write()函数保存为JPG可因压缩缺陷造成失真,因此加密与解密文件都保存为bmp格式,可避免失真,保证加解密件绝对完整.改进的混沌模型保留了原混沌的状态转移特性,在空间中构成了4个连接在一起的异变混沌堆,系统在4个堆轨道之间无序游走,产生加解密需要的异变混沌信号.
4 系统仿真与测试分析
4.1 密钥空间与性能
理论上讲,当信号放大参量I取最大值1016时,参数a最多有4×1015个取值,参数b、c在相似相态域中最多有1018个取值.若将所有相态纳入计算,3个参数将可以形成超过4×1087组完全不同的频道.这将是一个相当巨大的有效对称密钥空间,远高于文献[6,8,9]中实现的密钥数量(2256组),甚至远超估算得到的宇宙粒子数量总和(1080).安全系数很高,依靠暴力破解没有可能成功.
此外,相同硬件配置与win10操作系统环境下使用异变混沌堆算法对1.52Gb的视频文件进行加密时长测试,用时319931ms,且加密后文件大小不变;测试AES加密同一文件用时约为373464ms,且文件长度变为原来的两倍,还原文件时长同样翻倍.计算可得异变混沌堆算法每1000ms可加密4.75Mb数据,而AES算法每1000ms可加密4.07Mb数据.由于异变混沌堆算法与AES时间复杂度都是正线性增加的,故异变混沌堆算法比AES算法的加密速度要略微快,且空间利用优于AES算法.

图3 异变混沌堆空间举例示意图Fig.3 3D view of rosslermutatedchaotic stack example
4.2 序列无序性与密钥敏感度检验
为了验证异变混沌堆产生信号序列具有较强的无序性,并证明通过该算法加密得到的密文序列对频道的微调精度极为敏感,需进行微调邻近密钥时的序列分析实验.首先使用Anylogic进行测试[15],根据设计的模型搭建一个Rossler异变混沌堆系统动力学模型用于仿真统计分析.为比较微调相邻混沌堆序列之间的数值相似度,可计算序列上的曼哈顿距离进行比较.对于任意两个序列Sq1、Sq2,有平均曼哈顿距离
(22)
推广到m个序列进行组合计算,可得出平均曼哈顿距离矩阵:
(23)
进一步可计算得出同一相态轴上的总体平均曼哈顿距离:
(24)
(25)
此外,为评估微调相邻频道异变混沌堆序列的形态相似程度,可计算序列相态差异度:
(26)
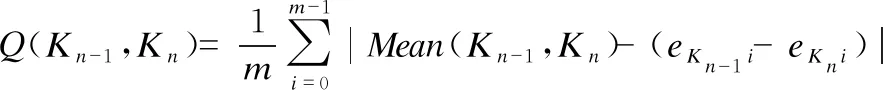
(27)
(28)
对两个完全相同的序列,有曼哈顿距离与相态差异度等于0,故曼哈顿距离、值方差和相态差异度越偏离0,序列差异越大.基于此可评估序列相似与差异水平.考虑Anylogic软件允许设置的参量最大不超过int类型上限,故暂时设置异变混沌堆系统信号放大参量I为107.任选多种混沌相态,在Anylogic中仿真,可计算得到表2所示不同相态下异变混沌堆产生序列的均值与方差;对铜号型一组的样本分布统计结果如图4所示.

表2 异变混沌堆各型态下三轴均值与方差Table 2 Mean and variance of triaxial in various types of mutatedchaotic stack

图4 混沌序列样本分布概率统计结果举例Fig.4 Statistical result example of sample distribution probability of chaotic sequences

表3 10位异变混沌堆序列样本Table 3 Sample of 10 locationsmutated chaotic stacksequence
由表2数据可知任意形态的原混沌经异变后的三轴序列方差都分别稳定在57、57、28附近,原混沌序列在不同相态下的方差表现出显著差异,而经过改进的异变混沌堆在不同相态下展现出平滑的平均值和方差.图4中第1行为原混沌三轴数据点分布情况,第2行则为对应异变混沌序列三轴点值分布.仿真实验中所有分布统计结都与图4中相似,不同相态的原混沌样本点值统计展现出明显特异性,而混沌堆的统计结果差异并不明显.
综上,异变混沌堆相较于原混沌模型具有更强的序列无序性和抗模式识别能力.由式(17)可推知,若设置参量I阶数高于7(例如最高取16),则获得的异变混沌堆序列无序度将更高,加密效果更好.
设异变混沌堆信号扩大参量I阶数为Rossler混沌值最高位数16,进行多个异变混沌堆序列的相似度分析实验.测试在默认混沌系统(a=0.2,b=0.2,c=4.6,x=y=z=0.1)上、以及分别对3个控制参微调亿分之一精度的三轴加密序列相似度,并观察加密效果.每个轴需测试4种相态,共生成12组序列.导出相同情况下三轴上分别产生的10位异变混沌堆序列如表3所示.
对表3各轴序列使用式(22)-式(28),计算可得序列相似度评价如表4所示:

表4 序列相似度评价Table 4 Sequence similarity evaluation
由表4结果可知,异变混沌堆算法在精度为亿分之一的微调下产生的样本序列两两之间具有远大于0的曼哈顿距离与相态差异度,序列间无序度较高.
综上,该加密方案对密钥的细微变化具有极强的敏感度,能够实现精度为亿分之一情况下的相邻密钥加密所得完全不同.由混沌系统对初始条件的敏感性可知:当两组密钥的数值距离更大时,也可保证密钥产生的混沌序列差异巨大.
4.3 信息熵
为验证异变混沌堆加密所得密件数据具有较高的随机分布特性和无序性,需计算信息熵H(m),m为信息源即明文或密文数据.根据信息熵的大小可以评估数据置乱效果是否均匀并比较密文与原文的相似程度.计算方式如式(29)所示:
(29)
此处选取了4张不同像素的Jpg图像,分别计算加密前后的信息熵以客观体现加密效果.一般情况认为一张图像的信息熵越接近于8,时,该图像的灰度分布越符合加密要求的效果,置乱像素点越均匀.此时图片可以很好地隐藏需要遮盖的重要信息.按式(29)计算得结果如表5所示:
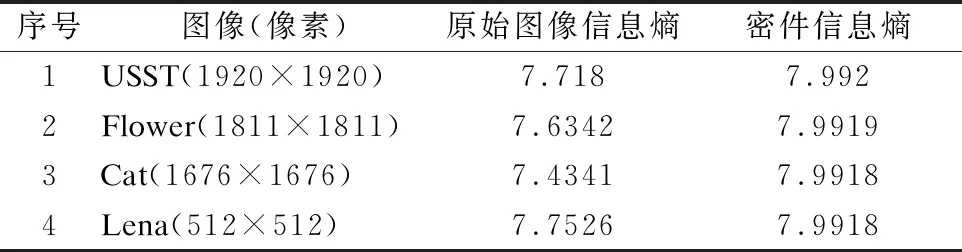
表5 信息熵测试结果Table 5 Test results of information entropy
根据表5中结果可知图像经过加密后信息熵显著逼近最优信息熵,图像数据置乱效果较为均匀;以测试序号4为例,实际加密前后后密件效果如图5所示,证实密件难以分析出任何有用信息.
4.4 对噪声干扰的鲁棒性
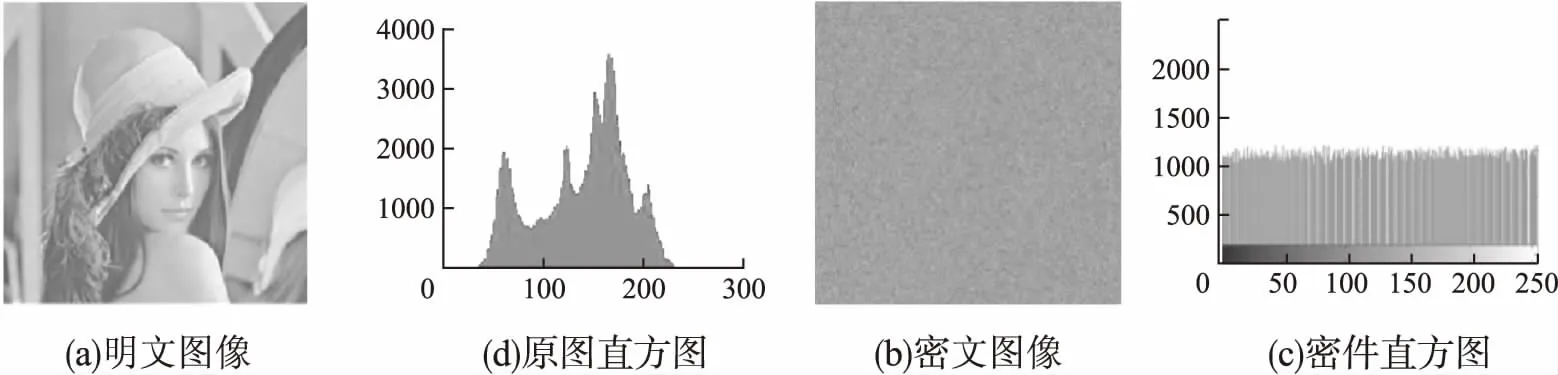
图5 原件与密件实际效果对比Fig.5 Comparison of the actual effect between the original and the secret
由文献[6,8,9]可知从简单的Logistic到复杂的二维Sine-Tent等混沌类加密算法已被证明普遍具有良好的抗差分、线性密码分析攻击的能力[6,8,9],故此处不再重复验证.但需要检验系统加密后的密件在传输中遭受噪声失真攻击后的鲁棒特性.为直观展现抗噪声干扰效果,考虑选择图片加解密进行实验分析.通过PS向测试密件中分别添加20%、30%、40%、50%的噪声干扰,使密件中数据被覆盖而丢失.添加的噪声符合高斯分布.对3个干扰后密件解密效果如图6所示.
若要更好的量化比较噪声干扰下算法的鲁棒性,可定义并计算图6中3个解密件与原图间的差异度,如式(30)所示:
(30)
其中k∈[0,W·H-1],P1,P2分别表示进行比较的两张图片,p1,k、p2,k表示两张图片在第k位上的像素值;W、H分别表示图像的宽、高,Pixel是最大像素值,取值为16777216.计算可得表6所示结果.
由表6数据可知在噪声干扰达到50%时,解密件图像仍然能保证差异度低于30%,图像中的关键信息大致能被传递识别,受干扰的解密件与原件之间特征相似度可达到70%以上,故算法在噪声干扰或传输失真情景下的鲁棒性良好.结合图6中噪声干扰密件解密的实际效果,可证实异变混沌堆加密解密算法具有一定抗噪声干扰能力.

图6 密件噪声干扰递增下解密件效果Fig.6 Effect of decryption under increasing noise interference

表6 解密件与原件差异度Table 6 Difference between the decryption and the original
5 结 论
通过在java中实现“异变混沌堆”加解密算法、结合RSA非对称加密算法开发了一套混合加解密系统.该系统能形成超大密钥空间,具备导入联系人公钥和频道配置信息密文、抄送加密后频道配置信息的混合加密功能,并可以按照要求进行任意大小文件、图像、文本的加密解密,具有普适性.
性能实验数据表明异变混沌堆加密算法效率略高于AES算法,所得的图像和文件密件与原件大小比例为1∶1,不但能够显著节省空间,在还原文件时还能比AES用时更少;由于异变混沌堆加密过程使用了分段计算混沌堆序列并释放资源的编程方式,故内存占用率能够显著降低.
经过仿真与实验,对不同相态下样本点的统计数据、亿分之一精度微调密钥时异变混沌堆序列相似度数据进行分析,证明了基于Rossler方程组改进设计的异变混沌堆算法能有效掩盖图像、文件、文字明文中的关键信息;且精度在亿分之一微调下用相邻密钥加密得到的密文差异极大,密钥高度敏感.经过信息熵监测与仿真噪声干扰解密测试,验证了该系统能产生符合要求的高度无序信号,并且在50%噪声覆盖下仍然能保留70%以上的关键信息,具有良好的鲁棒性.
