瞬时点源和连续源随流输移扩散

黄桢宇，沈良朵，陈浩民，黄桢蕾

(浙江海洋大学 港航与交通运输工程学院,浙江 舟山 316022)

近年来，随着航运业的不断发展，由船舶引发的燃油泄漏事故时有发生，对海洋环境有十分严重的影响。如何处理这类随流扩散污染物已成为人们关注的热点，其中污染物输移扩散的燃油泄漏规律研究尤为受到重视。近岸环流主要出现在缓坡海域波浪破碎之后形成的波浪破波区，近岸环流速度沿水深的铅直分布是不均匀的。由于近岸缓坡海域波浪破碎区水深较浅，近岸环境速度的这种不均匀性可忽略，认为流速沿水深混合充分、均匀，把运动简化为平面二维运动。[1]以往的研究普遍认为潮流是污染物输移扩散的主要驱动力[2]，这种分析方式适用于在远海和拥有岩石陡坡地形的近海环境。然而，在近岸缓坡地形条件下不能忽略波浪对物质输移的影响。目前，国内对近岸污染物扩散问题只进行了试探性研究。例如：孙涛等[3]和陶建华等[4]主要研究基于数学模型的波浪作用对近岸污染物扩散的影响；丁雷[5]主要在解析法上对污染物紊动扩散系数进行推导研究；彭云[6]采用物理模型研究船舶燃油泄漏之后水体污染物的扩散特征；武周虎等[7]研究变扩散系数下三维浓度的扩散问题；江春波等[8]主要针对二维物质输移扩散问题提出有限体积算法。国外学者对比也做了相应的研究。[9-12]

基于上述研究成果，本文以瞬时点源和连续源污染物为研究对象，给出无限区域点源和连续源污染物浓度解析解、数值解和墨水扩散试验。在此基础上，对简单波流场下点源和连续源污染物浓度输移扩散特征进行研究。

1 瞬时点源解析解

不考虑对流输移扩散情况下的二维扩散方程为

(1)

式(1)中:C为深度平均的污染物浓度；Dcwx和Dcwy分别为在波流作用下污染物沿x和y方向的扩散系数。

由于Oxy平面上的某点浓度在x方向和y方向相互独立，故某点的浓度C(x,y,t)可由2部分乘积构成，即

C(x，y，t)=C1(x，t)×C2(y，t),

C1≥0;C2≥0

(2)

式(2)中:C1和C2分别为x方向和y方向深度平均的污染物浓度。

瞬时点源质量M为

(3)

S={(x,y)|x2+y2≤R2}

(4)

式(3)和式(4)中：M1和M2分别为瞬时点源在深度平均的x和y方向的分质量。

将式(2)代入式(1)可得

(5)

由浓度分布的对称性，有

(6)

式(6)中的瞬时点源解析式分别为

(7)

由式(2)可得二维扩散方程的瞬时点源解为

(8)

各向同性情况下有

Dcwx=Dcwy=D

(9)

将式(9)代入式(8)可进一步化简为

(10)

考虑点源位置(x0,y0)随流输移速U和v可得浓度解析解为

(11)

2 连续源解析解

根据瞬时点源解析解推导过程，对于无限区域，将式(8)进行叠加可得到连续源解析解，经过时间t后连续源微元浓度的解析解为

(12)

对等式两边积分，有

(13)

由于积分结果无法用基本初等函数表示，因此需借助三维空间，采用由三维到二维的方法将该问题设想为有一系列厚度为dx的薄片(见图1),假设波流场以一个和沿x正方向的速度u经过与坐标原点重合的源点O，此时每一薄片接受的污染物质量为Mdτ(dτ为每一薄片通过源点的历时dτ=dx/u)，然后在平面上做横向扩散(如图1所示)，根据二维扩散的瞬时点源解，薄片中单位面积上的质量为

(14)

式(14)中:Dcwz和Dcwy分别为波流作用下污染物沿z和y方向的扩散系数。

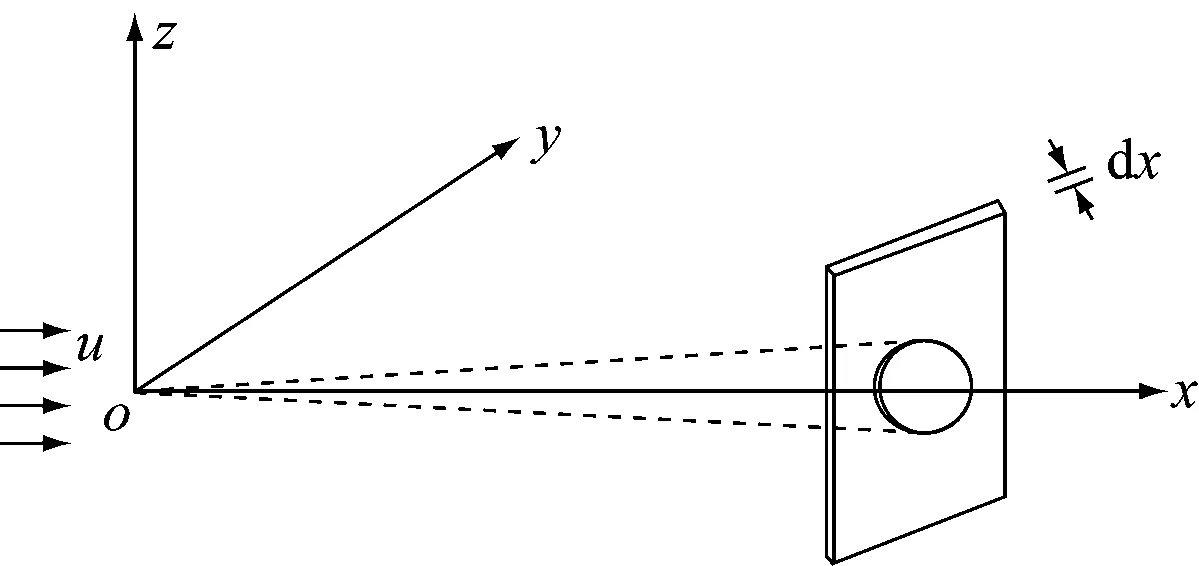
图1 连续源三维推导图

薄片的位置由x=ut给出，且三维的浓度是薄片单位上的质量除以厚度，因此其解为

(15)

由于是在简单波流畅情况下,因此有Dcwz=Dcwy=D，令r2=z2+y2，并将其代入式(14)，化简得

(16)

根据式(16)，令z为0，可将其转化为二维解析式

(17)

令无量纲浓度为

原解析式即为

(18)

3 数值求解

3.1 基本控制方程

深度平均的二维对流输移扩散方程为

(19)

式(19)中:H为波高；SW为污染物源汇项。

3.2 扩散系数

3.2.1纯水流作用下的扩散系数

纯水流作用下深度平均的污染物扩散系数为

(20)

(21)

式(20)和式(21)中：Dcx和Dcy为流作用下污染物沿x和y方向的扩散系数；K为谢才系数;k1和k2分别取5.93和0.15。

3.2.2纯波浪作用下的扩散系数

纯波浪作用下污染物扩散系数为

(22)

式(22)中:Dwx和Dwy分别为波流作用下污染物沿x和y方向的扩散系数;h为当地水深；H=h+η;η为波高与当地水深的差值；T为波浪周期;破碎区α1=5.5η/h，非破碎区α1=1.0。

3.2.3波流共同作用下的扩散系数

在波浪和潮流作用下污染物扩散系数可采用比较简单的线性迭代法得到，即

Dcw=Dc+Dw

(23)

3.3 边界条件

在一个面积很大的海域，周边边界对污染物的影响非常小，可用以下边界条件：

1) 当流体流入计算区域时，边界处浓度可置为域外值，即C=0。

2) 当流体流出计算区域时，根据实际情况，可给定边界条件为

(24)

式(24)中:v为边界处流速矢量。

一般情况下可采用更简洁的连续边界条件，即

(25)

式(25)中:n为边界外法线方向。

4 结果比较

4.1 点源扩散

当计算区域足够大时，可忽略边界影响，与理论推导的无限区域情况相近。扩散范围300 000 m×300 000 m；初始点源放在区域中心位置；为简化计算，取各向同性，水平速度为U=v=0.5 m/s；D=Dcwx=Dcwy=10 000 m2/s，M=10 000 000个单位质量；为使计算稳定并快速得到计算结果，空间步长取Δx=Δy=3 000 m,时间步长取Δt=10 s。

为便于比较分析初始阶段和稳定阶段点源解析解和数值解，当点源解析解和数值解为1 000 s和5 000 s时，相应浓度分布三维图分别见图2和图3。当点源解析解和数值解分别为1 000 s和5 000 s时，相应浓度分布等值线比较见图4和图5。

a) 解析解

a) 解析解

图4 点源解析解数值解1 000 s等值线对比图 图5 点源解析解数值解5 000 s等值线对比图

由图2～图5可知:在简单各向同性波流场下，点源随流扩散数值解与解析解吻合良好，呈现出圆环状分布；浓度值由中心向外部递减，随着时间的推移，相同圆环半径处的污染物浓度下降。

4.2 连续源扩散

模型计算区域和参数选取与点源情况一致。当连续源解析解和数值解为1 000 s时，相应浓度分布三维图见图6。连续源解析解和数值解无量纲化等值线对比见图7；连续源污染物扩散中某点浓度随时间变化图见图8。

a) 解析解

图7 连续源解析解和数值解无量纲化等值线对比

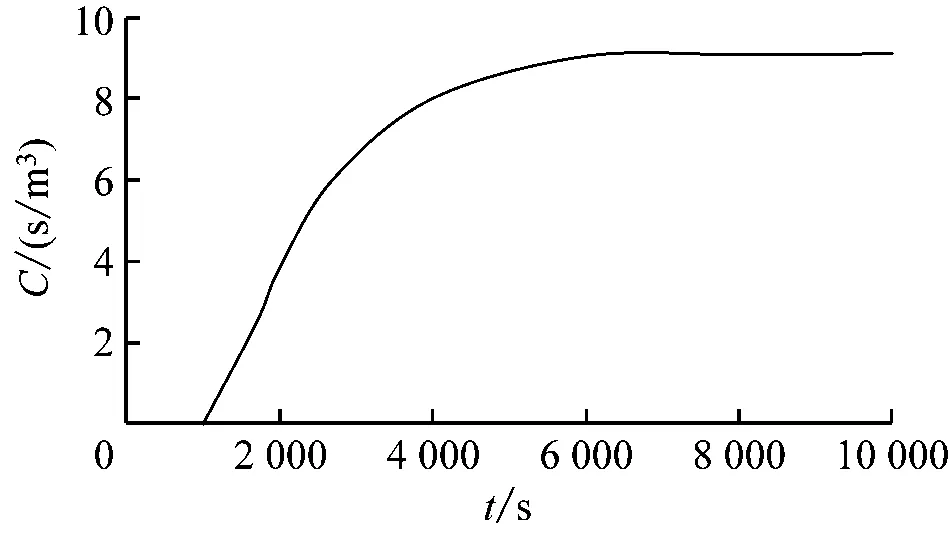
图8 连续源某点浓度随时间的变化曲线

由图6和图7可知:在各向同性简单波流场下，连续源随流输移扩散数值解与解析解吻合良好，浓度随空间呈椭圆分布，距离源点越远，相对浓度越小。由图8可知:随着时间的推移，距离投放源点固定位置处的污染物浓度趋于一个稳定值。

5 试验数值结果比较

本文结合文献[1]中的点源和连续源墨水扩散试验进行比较分析，其坐标示意见图9。取工况3和工况6，坡度为1∶40，波浪入射位置的静水深h=0.45 m，波浪入射角θ=30°，入射波高H0=0.05 m，入射波周期T=2 s，瞬时点源取源项=C(3，4)=1，连续源取源项Sm(3，4)=0.1(坐标表示投放点距离静水线3 m，距离沿岸流上游4 m)；计算参数参考文献[1]中的数据(紊动混掺系数N=0.001 2，波浪破碎指标γ=0.7，波流场底摩擦因数cf=0.006，空间步长根据要求为Δx=Δy=0.2 m，时间步长Δt=0.1 s)，点源和连续源试验及其计算结果分别见图10和图11，其中浓度等值线从内到外依次为100%、30%和5%。

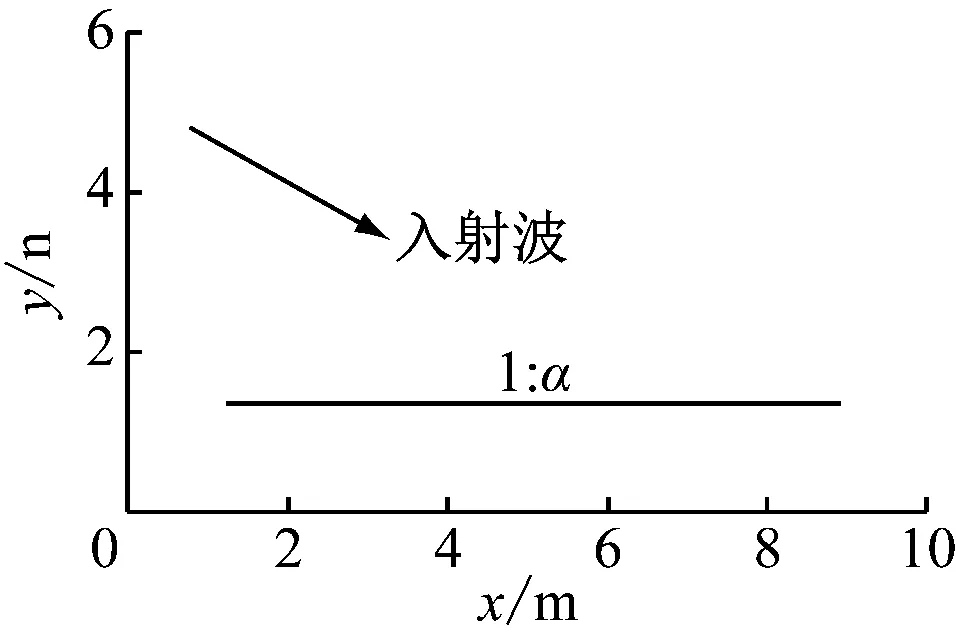
图9 物质扩散模型坐标示意

a) t=22 s

c) t=32 s

a) t=32 s

c) t=52 s

由图10和图11可知:同一时刻点源计算结果和试验结果较为吻合，进一步表明该数值模型能较好地模拟点源的实际扩散效应。与点源椭圆分布不同的是，连续源浓度最大值点并不在中心，而是在投放源点位置处。

6 结束语

本文结合二维对流输移扩散瞬间点源和连续源的解析解、数值模型以及墨水扩散试验得出瞬时点源和连续源在各向同性的简单波流场环境下的浓度输移扩散分布特征，即：瞬时点源呈圆环分布浓度值由中心向外部递减，随着时间推移，相同圆环半径处污染物浓度降低；连续源浓度随空间呈椭圆分布，距离源点越远，相对浓度越小，随着时间的推移，距离投放源点固定位置处污染物浓度将趋于一个稳定值。