Mg-RE-Zn-Zr 合金的热变形行为和加工图研究
2020-12-08夏祥生陈文黄少东胡传凯吴洋张奎马明龙
夏祥生 ,陈文,黄少东,胡传凯,吴洋,张奎,马明龙
(1.中国兵器工业第五九研究所,重庆 400039;2.有研科技集团有限公司 有色金属材料制备加工国家重点实验室,北京 101407)
镁合金是一种轻质的金属材料,在电子、航空、航天和汽车工业的应用前景广阔[1—2]。目前商用的镁合金由于强度低和热稳定性差限制了其应用范围,与传统的AZ31,ZK60,AZ80 镁合金相比,含有稀土元素的镁合金表现出良好的沉淀强化效应[3—4]。在Mg-RE 合金研究基础上,向合金中添加Zn 元素,由于固溶、时效和长周期堆积有序(LPSO)结构的强化,还可以进一步提高其力学性能[5—6],因此,Mg-REZn-Zr 合金受到了越来越多研究人员的关注[7—8]。
塑性变形(如挤压、轧制和锻造)通常用于改善合金的力学性能[9—10],由于镁合金是密排六方晶系结构,其室温成形性较差,但在高温下成形时,热激活可使非基底滑移开动,塑性变形能力得到大幅提高。对于Mg-RE-Zn-Zr 合金来说,合金中形成了一种新的LPSO 结构,表现为18R,24R,10H 等不同类型[11—12],目前对其热变形行为和加工图的研究相对有限,因此,有必要研究Mg-RE-Zn-Zr 合金在各种特定变形条件下的变形特性及塑性成形区间,为该合金的变形参数制定提供理论基础。
1 实验
实验合金化学成分为Mg-8.49%Gd-4.49%Y-0.74%Zn-0.38%Zr(质量分数),经均匀化后在铸锭上切取Φ8 mm×12 mm 的圆柱形试样。
采用Gleeble 3500 热机械模拟机,在变形温度300~500 ℃,应变速率0.001~1 s–1范围内进行等温压缩实验,最大真应变为0.91。首先在试样的两端添加石墨片以减少摩擦,然后将试样加热到所需温度,并保温2 min 使试样温度均匀,压缩实验完成后,试样水淬以保留高温变形组织。在平行于压缩轴的中心切取光学显微镜试样,然后研磨和抛光后,在体积分数为4%硝酸酒精溶液中腐蚀。
2 结果及分析
2.1 流变应力特征
图1 所示为不同条件下合金的真应力-真应变曲线。从图1 可见,真应力-真应变曲线在整个变形条件下具有相似的特征,即在变形初始阶段,应力随着应变的增加而增加,表明加工硬化占主导,之后流动应力达到最大值,然后流动应力减小,达到稳定状态。

图1 不同变形条件下的真应力-真应变曲线Fig.1 True stress-true strain curves at different deformation conditions
图2 显示了应变为0.2 时峰值流动应力随温度的变化。可见,在确定的应变速率下,流动应力随着温度的升高而减小,而在给定的变形温度下,流动应力随着应变速率的增加而增加。当变形温度为300 ℃,变形速率为0.1 s−1和1 s−1时,试样发生了早期开裂。
2.2 合金的本构方程
修正的Arrhenius 函数是最常用的本构方程,通常用于描述热变形过程中应变速率、变形温度和流动应力之间的关系[13]。

图2 真应变0.2 时流变应力与变形温度和变形速率的关系Fig.2 Variation of flow stress with deformation temperature and strain rate at a true strain of 0.2
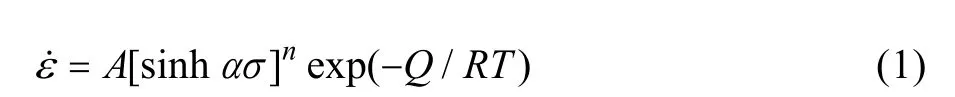
式中:A和α是材料常数;n是应力指数;Q是热变形激活能;T是绝对温度;R是气体常数;σ是给定应变的流动应力。文中取真应变为0.2 时的应力为流动应力。低流应力下(ασ<0.8),式(1)可描述为:

在高应力下(ασ>0.8),式(1)可描述为:
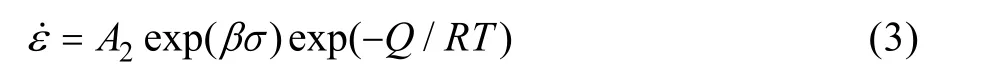
式中:A1和A2是材料常数。式(2)和式(3)可以简化为:

对式(1)两边取自然对数,可得:
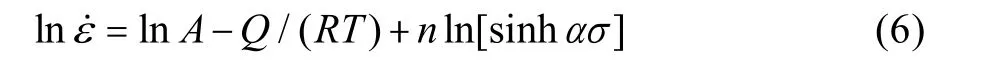
若为常数,取式(6)偏微分方程可得:

根据式(7),Q值可以写成Q=Rn'D,n'值是关系的斜率,而D是ln[sinhασ]-1000/T关系的斜率,从图4 可得n'和D值分别为4.127 和6.657,因此可得实验合金的Q值为228.414 kJ/mol。

图3 ln和ln σ 与σ 的关系Fig.3 Relationship between lnε˙& ln σ and σ

图4 ln和ln[sinh ασ]与1000/T 的关系Fig.4 Relationship between lnε˙ & ln[sinh ασ] and 1000/T
通常也可采用Zener-Hollomon 参数来表示应变速率和变形温度对流动应力的影响,可表述为[14]:
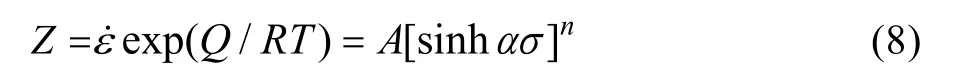
式中:n为应力指数。对式(8)简化可得:

根据式(9)可得n=dlnZ/dln[sinhασ],n的值是lnZ-ln[sinhασ]关系图中直线的斜率,由图5 可得斜率的平均值为n=4.076,其拟合曲线的截距为 lnA=34.949,可得A=1.507×1015s–1。
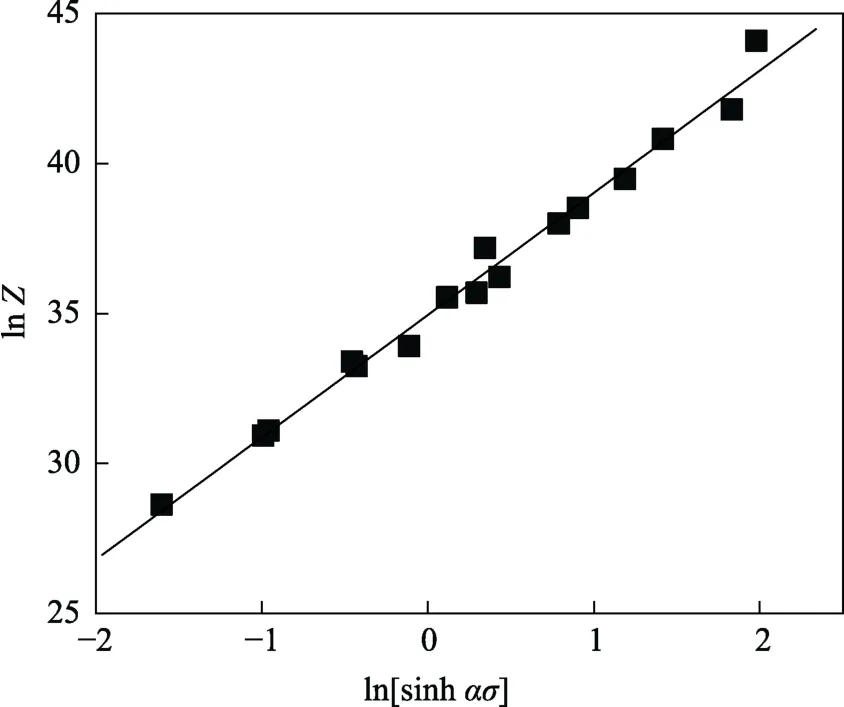
图5 ln Z 和ln[sinh ασ]的关系Fig.5 Relationship between ln Z and ln[sinh ασ]
根据上述得到的参数,根据式(1),本构方程可以表示为:
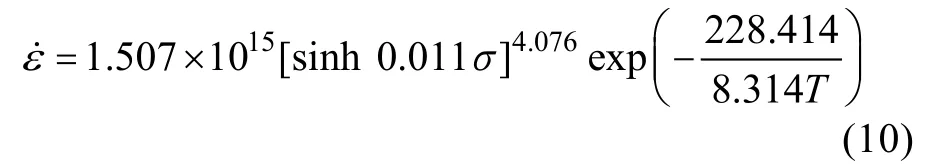
表1 列出了不同镁合金变形激活能值的大小,文中合金的变形激活能为228.414 kJ/mol,普遍高于无LPSO 结构的镁合金。在塑性变形理论中,变形激活能是表征变形难度的一个重要物理参数,变形激活能越高,势垒越大,塑性变形越困难,说明LPSO 结构使变形更加困难。
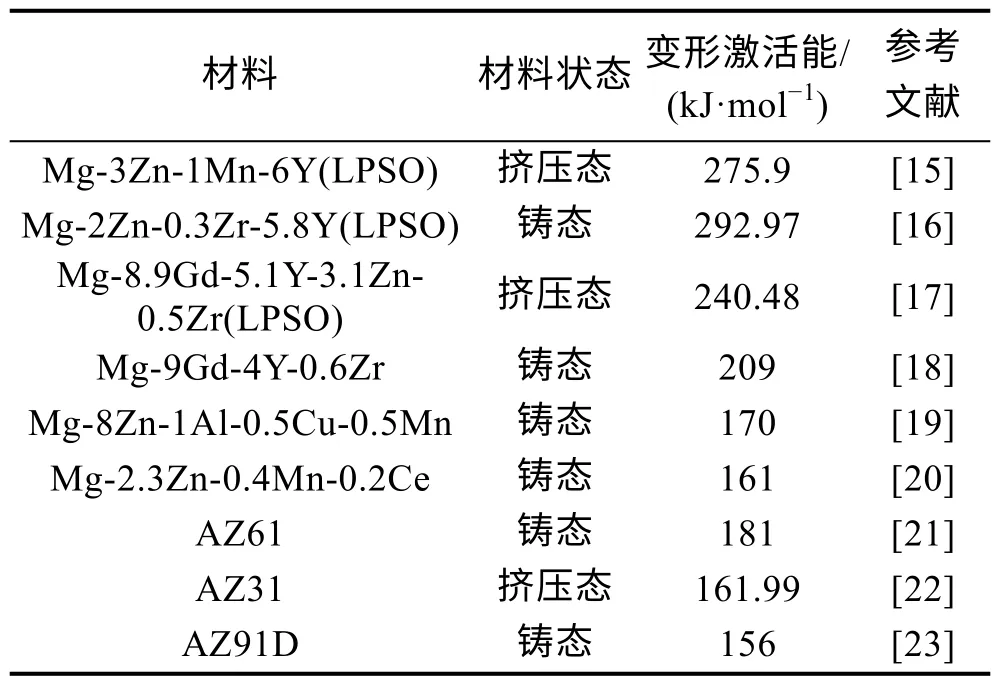
表1 不同镁合金变形激活能的对比Tab.1 Comparison of activation energy values for various magnesium alloys
图6 所示为变形前合金在LPSO 结构、晶粒内部和近晶界处的硬度分布。LPSO 结构的硬度大于晶粒内部的硬度,近晶界处的硬度最小。块状LPSO 结构具有热稳定性,是位错运动的有效屏障,需更多的能量实现位错的交叉滑移和攀移。Prasad 等报告了类似的情况,并将高的变形激活值归因于基体中存在CaMgSn 金属间化合物颗粒[24]。
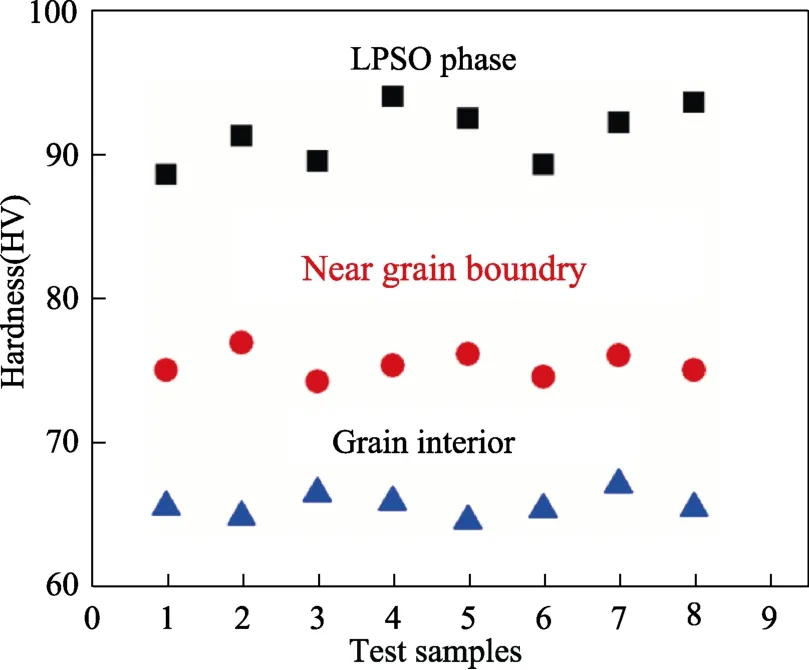
图6 变形前在LPSO 结构、晶粒内部和近晶界附近的硬度分布Fig.6 Hardness distribution of the alloy at LPSO phase,grain interior and near grain boundary
2.3 本构方程的应变补偿
由式(10)可知,流动应力仅取决于变形温度和应变速率,没有考虑应变的影响。许多先前的研究表明应变对α,n,Q,lnA的值有明显的影响[25—26],因此,应在Arrhenius 模型中引入应变补偿,以更准确地预测流动应力。根据上述计算过程,在不同应变下,求得α,n,Q,lnA的值,如图7 所示,并采用五阶多项式函数对α,n,Q,lnA与应变之间的关系进行拟合,拟合结果如图7 所示,其中α0=0.012 35,α1=–0.023 48,α2=0.093 95,α3=–0.106 81,α4=0.030 36,α5=0.005 78;n0=5.696 12,n1=–15.196 69,n2=51.891 17,n3=–99.713 1,n4=96.731 33,n5=–36.819 33;Q0=242.849 57,Q1=–269.812 25,Q2=1712.287 91,Q3=–4659.472 95,Q4=5427.283 89,Q5=–2310.202 37;A0=36.320 62,A1=–34.659 11,A2=249.303 35,A3=–715.730 03,A4=855.592 64,A5=–369.593 09。

特定应变下的流动应力可通过Zener-Holloman参数的函数进行预测:

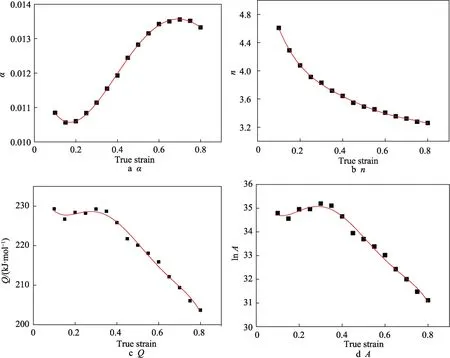
图7 α,n,Q,ln A 与应变的变化规律Fig.7 Variations of α,n,Q,ln A with strain
2.4 本构方程的验证
图8 所示为不同条件下的实验和预测流动应力。在整个实验范围内,预测的流动应力值与实验值吻合良好。为了进一步评估本构方程的精度,采用了相关系数(R)和平均绝对相对误差(EAARE)来说明,其表达式如下:

所有的实验和预测数据如图9 所示,大多数流动应力数据点都靠近拟合线,且R和EAARE值分别为0.988 和7.53%,高R值和低EAARE值表明预测数据和实验数据之间具有良好的相关性,因此,将式(10)和式(11)结合起来,就可以得到实验合金不同应变下的本构方程。
2.5 加工图
Prasad 等[27]在动态材料模型的基础上建立了加工图。Prasad 认为,工件在热变形过程中可以视为功率耗散体,输入系统能量P可分为两部分:G含量和J共含量。G含量表示通过塑性变形产生的功耗,J共含量表示通过微观结构转变产生的功耗,大部分的G含量都转化为粘塑性热量,J共含量的微观结构转变包括动态再结晶、相变等。输入系统能量P可表示为:

对于某一确定的变形条件,流动应力可表示为:

式中:K为材料常数;m为材料的应变速率敏感系数,其可表示为:

采用3 次样条插值法来描述lnσ和lnε˙之间的关系,其可表示为:
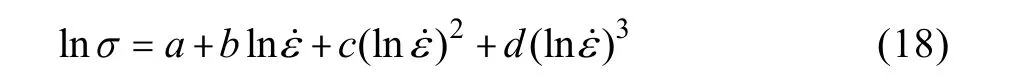
式中:a,b,c,d是材料参数。在任何确定的变形条件下,J含量可表示为:
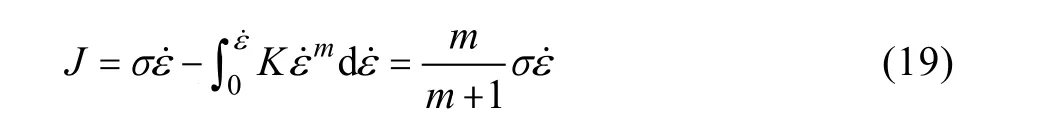
对于理想的线性耗散体,m=1 和功耗的耗散可以通过功耗的效率(η)来表示:
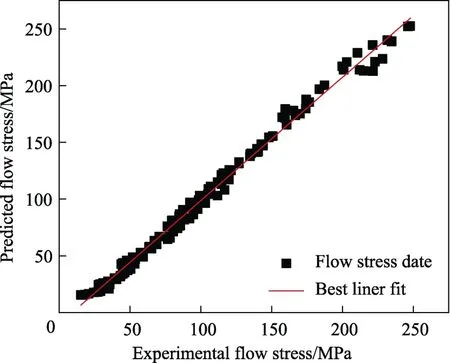
图9 实验和预测流变应力的对比分析Fig.9 Correlation between the experimental and predicted flow stress
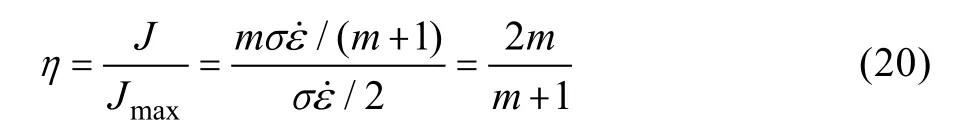
可以通过η随变形温度和应变速率的变化来获得功率耗散图。考虑流动不稳定性出现的连续性准则,可得到材料流变失稳判据为:
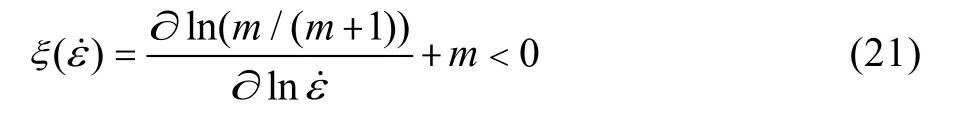
ξ是失稳参数,可以通过ξ随变形温度和应变速率的变化获得失稳图,失稳图可以分为两部分:第一个是失稳区,其中ξ<0,第二个是可加工区,其中ξ>0。通过将功率耗散图与失稳图叠加可以得到加工图。
合金在0.3,0.5,0.7,0.9 应变下的功率耗散图如图10 所示。在功率耗散图中,等值线代表了功耗的百分比效率,它表征了热加工过程中微观结构的演变速度。可以发现,在应变为0.3 时,功率耗散图表现出两个高功率耗散效率域。第一个区域出现在350~420 ℃的温度范围内,应变速率在0.001~0.01 s–1之间,最大效率为 40%;第二个区域出现在 420~480 ℃的温度范围内,应变速率在0.005~0.1 s–1之间,最大效率为48%。此外,在图10a 可以观察到具有较低功耗效率的3 个区域。第一个区域出现在350~400 ℃的温度范围内,应变速率在0.1~1 s–1之间;第二个区域出现在400~500 ℃的温度范围内,应变速率在0.13~1 s–1之间;第三个区域出现在430~500 ℃的温度范围内,应变速率在0.001~0.003 s–1之间。图11所示为功率耗散因子随应变的变化规律,可见,功率耗散因子随应变的变化不大,说明应变对变形的影响较小。功率耗散图可用于反映变形过程中合金的微观结构演变,功率耗散的低值区域通常与微裂纹的萌生和增长或其他变形破坏有关[28—29]。一般来说,镁合金发生动态再结晶区域的有效值约为30%~50%[30—31],通常对应于可加工区域。

图10 不同真应变下的功率耗散图Fig.10 Power dissipation maps of at different true strains

图11 应变速率0.01 s–1 条件下功率耗散因子随应变的变化规律Fig.11 Variation in efficiency of power dissipation with true strain at the strain rate of 0.01 s–1
图12 所示为合金在0.9 真实应变下的加工图,品红色区域表示失稳区。加工图中有两个高功率损耗效率区域,第一个区域在较低的应变速率和温度范围内,第二个区域在中等应变速率和较高温度范围内,加工图中只存在一个失稳区,出现在变形温度为350~500℃,应变速率为0.1~1 s–1之间,而且低温下的失稳区面积大于高温下的失稳区面积。
图13 所示为加工图中两个高功率损耗区的典型显微组织。图13a 为400 ℃/0.001 s–1条件下的变形组织,显微组织为粗细晶粒组成的双峰结构,表明在该区域内发生了不完全动态再结晶。图13b 为450 ℃/0.01 s–1下的变形组织,其与400 ℃/0.001 s–1变形试样相比,动态再结晶晶粒的体积分数有所增加,因此,可以得出两个高功率损耗区的变形机制都为动态再结晶。Li 等[18]研究了Mg-9Gd-4Y-0.6Zr 合金的工艺参数,发现合理的工艺参数为变形温度为430~450 ℃和应变速率为0.006~0.03 s–1。周等[32]研究了挤压态Mg-9.8Gd-2.7Y-0.4Zr-合金的加工图,得出合理的工艺参数为:温度为420~450 ℃,应变速率为0.01~0.1 s–1,该区域的变形机制为动态再结晶。文中合金的可加工窗口比Mg-Gd-Y-Zr 镁合金要宽得多,这两种合金最大的区别是锌的加入,文中在Mg-Gd-Y-Zr合金中添加质量分数为0.7%的Zn 形成细小的层状LPSO 结构,该结构的存在可改善合金的加工性能[33]。失稳区域变形试样的形貌如图14 所示,失稳变形试样由于应力集中而出现宏观开裂,压缩轴与开裂方向的夹角约为45°。
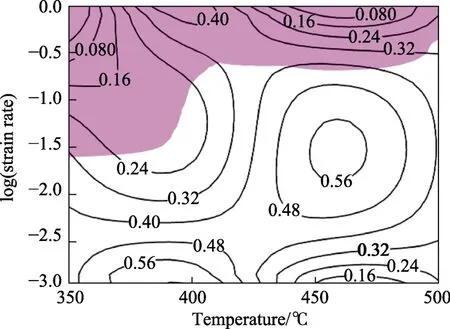
图12 实验合金真应变0.9 时的加工图Fig.12 Processing map of the experimental alloy at strain of 0.9
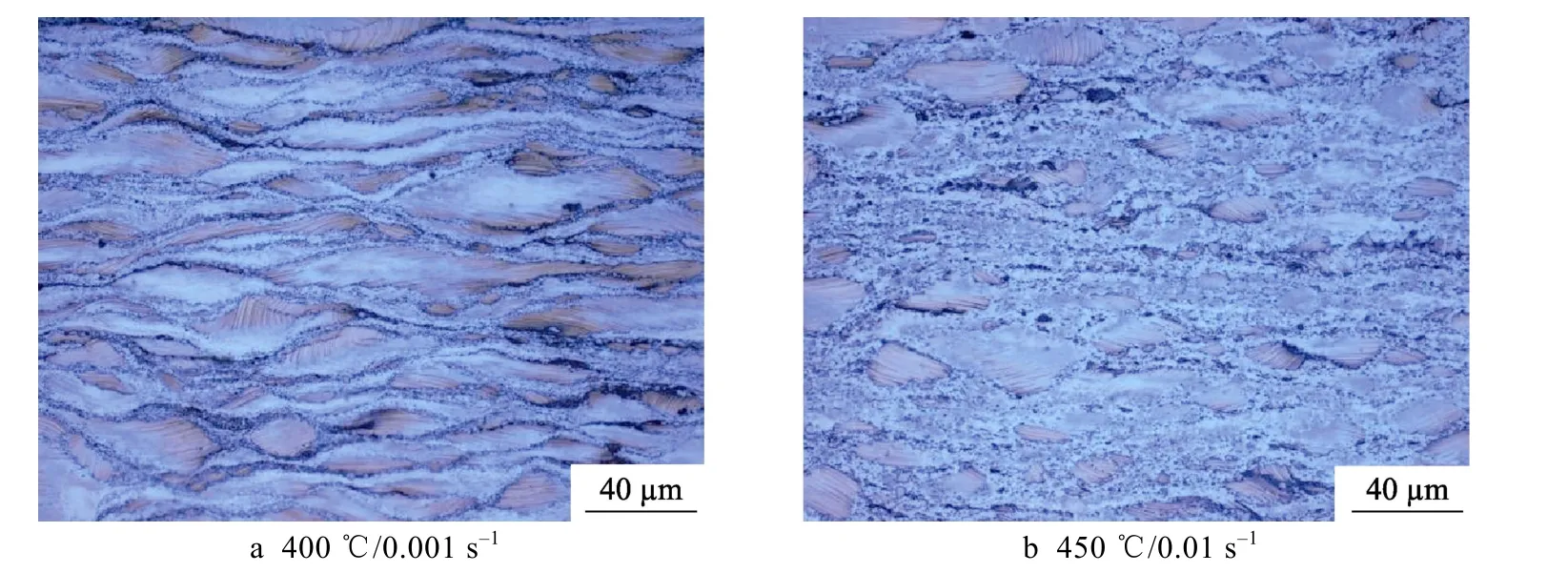
图13 实验合金不同变形条件下的显微组织Fig.13 Microstructures of the experimental alloy deformed at different conditions

图14 失稳区域变形试样形貌Fig.14 Morphology of the sample deformed in the instability domain
3 结论
通过等温压缩实验研究了Mg-8.5Gd-4.5Y-0.7Zn-0.4Zr 合金的高温变形特性,建立了带有应变补偿的Arrhenius 方程和加工图,得出以下结论。
1)变形条件对流动应力的影响较大,其随应变速率的升高和变形温度的降低而增加。当在变形温度为300 ℃,变形速率为0.1 s–1和1 s–1时,试样会发生早期开裂。
2)Mg-8.5Gd-4.5Y-0.7Zn-0.4Zr 合金的本构方程
3)α,n,Q,lnA和应变之间的关系可由五阶多项式函数进行拟合,由带有应变的本构方程得到的预测流动应力值与实验值吻合良好。
4)加工图中存在两个可加工区域,第一个区域在变形温度为350~420 ℃,应变速率为0.001~0.01 s–1的范围内,第二个区域在变形温度为420~480 ℃,应变速率为0.005~0.1 s–1的范围内,两个可加工区域的变形机制都为动态再结晶。
