基于分数阶PIλDμ的非线性分数阶主动控制悬架研究
2020-12-08常宇健田沃沃陈恩利邢武策
常宇健,田沃沃,金 格,陈恩利,邢武策
(1.石家庄铁道大学 电气与电子工程学院,河北 石家庄 050043;2.石家庄铁道大学 机械工程学院,河北 石家庄 050043)
0 引言
目前针对汽车悬架系统的主动控制主要以线性阻尼模型为研究背景,并没有考虑悬架系统中阻尼材料的记忆特性。因此国内外学者利用分数阶模型能够准确描述物体记忆特性的优点,将分数阶微积分引入到汽车悬架系统的建模和控制研究中。文献[1]首次提出CRONE悬架模型,即利用分数阶模型替代传统被动悬架中线性弹簧和阻尼器模型。文献[2-4]针对油气悬架的整数阶模型不能准确描述其多相介质力学特点,提出采用分数阶微积分理论建立其Bagley-Torvik方程,并验证了分数阶模型的可行性。文献[5]将分数阶微分引入到液压气动悬架系统建模中,并通过仿真和实验证明了分数阶液压气动悬架模型的有效性。文献[6]提出一种能够准确描述空气弹簧记忆特性的分数阶模型。文献[7]利用分数阶模型描述磁流变阻尼器的阻尼特性,该模型比整数阶模型具有更高的拟合精度。文献[8]建立了MR阻尼器的分数阶模型,并且分析了该模型的动力学特性。综上所述,分数阶微积分理论在汽车悬架系统建模中具有更好的适用性及有效性,为今后分数阶悬架模型的研究奠定了基础。
为了改善传统整数阶PID控制器的性能,文献[9]提出了分数阶PIλDμ控制器,由于增加了控制参数(λ和μ)使得比整数阶PID控制具有更宽的整定参数范围[10]。文献[11-13]分别将分数阶PIλDμ控制算法引入到列车自动驾驶系统的速度控制、冷轧液压伺服位置控制以及汽车电子节气门的精确跟踪控制中,研究结果表明,分数阶PIλDμ控制算法在速度和位置控制中能够快速、准确地跟随输入信号,并且能明显抑制外在干扰和系统参数扰动。基于分数阶PIλDμ控制具有良好的控制性能,众多学者针对非线性悬架系统分别设计了分数阶PDμ[14-15]、PIλDμ[16-17]和IλDμ[18]控制器,研究结果表明,分数阶PIλDμ控制具有更灵活的调节结构,能够有效改善汽车的动态性能。
虽然分数阶PIλDμ控制在非线性悬架系统主动控制中得到广泛的研究与应用,但是对于非线性分数阶悬架的主动控制研究则相对较少。文献[19-20]对汽车悬架系统中的线性阻尼成分进行改进,建立由分数阶阻尼和非线性弹簧组成的悬架系统,并采用整数阶PID控制和分数阶PIλDμ控制改善汽车的行驶性能。然而,该研究仅仅以磁流变悬架系统为研究对象,而且忽略了分数阶磁流变Bingham模型中补偿器产生的力和库伦阻尼力,从而导致分数阶悬架模型的主动控制研究具有一定的局限性。因此本文在包含线性刚度和线性阻尼的传统悬架模型基础上进行改进,增加了非线性刚度和分数阶阻尼,使分数阶悬架模型具有更广的适用范围。
本文基于分数阶微积分理论建立了1/4车二自由度非线性分数阶悬架系统动力学模型,采用遗传算法对整数阶PID控制器和分数阶PIλDμ控制器进行参数优化,利用MATLAB/Simulink进行主动控制仿真研究,并与被动控制悬架系统时域响应进行对比分析。
1 非线性分数阶悬架系统建模
1.1 1/4车主动控制悬架振动模型
1/4车二自由度非线性分数阶主动控制悬架系统结构图如图1所示。
由图1可知,非线性分数阶主动控制悬架系统中弹性力包括一次线性恢复力和三次非线性恢复力,即
Fs=ks(zs-zu)+εks(zs-zu)3,
(1)
式中,zs为簧载质量位移,zu为非簧载质量位移,ks为弹簧刚度,εks为非线性弹簧刚度,ε为非线性系数。
主动控制悬架系统中线性阻尼力为

(2)
式中,c为悬架等效阻尼系数。
分数阶微积分主要有3种定义方式[21],即Riemann-Liouville、Grunwald-Letnikov和Caputo。本文利用Caputo分数阶微分描述悬架系统中的分数阶阻尼力,Caputo定义式为

(3)
其中,Γ(z)满足Γ(z+1)=Γ(z)。
分数阶阻尼力为
Fc=hDp(zs-zu),
(4)
式中,Dp是分数阶微分算子,h为分数阶系数,p为分数阶阶次且满足0≤p≤1。
根据牛顿第二定律建立该系统的微分方程为
(5)
式中,ms为簧载质量,mu为非簧载质量,zr为路面位移,kt为轮胎刚度,u为主动控制力。
1/4车二自由度非线性分数阶悬架系统参数选取为ms=240 kg,mu=36 kg,ks=16 000 N/m,ε=0.1,c=1 650 N·s/m,kt=160 000 N/m,h=1 000,p=0.5[22]。
1.2 Oustaloup滤波器设计
为了方便利用MATLAB/Simulink对含分数阶微分项的非线性悬架系统进行仿真分析,本文利用Oustaloup滤波器算法[23]对悬架系统中分数阶微分算子近似计算,即在选定的频率段(ωb,ωh)内对sp近似替代,构造Oustaloup滤波器为

(6)
式中,M为滤波器阶次,滤波器的零点为
极点为
根据上述Oustaloup滤波器算法,构造频率段为(0.001 rad/s, 1 000 rad/s),阶次为M=5的Oustaloup滤波器。
1.3 随机路面输入建模
为了能够真实反映汽车在实际路面的行驶性能,本文建立随机滤波白噪声数学模型作为1/4车二自由度非线性分数阶主动控制悬架系统的输入模型,即
(7)
式中,q(t)=zr(t)为路面位移,η1为下截止空间频率,η1=0.011 m-1,v1为车速,v1=10 m/s,η0为参考空间频率,η0=0.1 m-1,Gq(η0)为路面不平度系数,Gq(η0)=256×10-6m2/m-1,w(t)是均值为0、方差为1的Gauss白噪声。
2 分数阶PIλDμ控制器优化设计
2.1 分数阶PIλDμ控制器设计
为了提高汽车的行驶平顺性和操纵稳定性,本文以非线性分数阶悬架系统的车身加速度、悬架动挠度和轮胎动位移为控制量,并将其期望值均设置为0,分别设计3个分数阶PIλDμ控制器进行主动控制研究。
构造分数阶PIλDμ控制器参数优化目标函数为
q3(zu-zr)2]dt,
(8)
式中,q1、q2、q3为加权系数,分别取0.5、0.3、0.2。
分数阶PIλDμ控制器的输入信号为
(9)
分数阶PIλDμ控制器的输出信号为
(10)
式中,kPi、kIi、kDi(i=1、2、3)分别为比例、积分和微分系数。
通过对式(10)进行拉普拉斯变换可得分数阶PIλDμ控制器传递函数为
(11)
式中,sμ、s-λ为分数阶微积分算子,本文利用Oustaloup滤波器算法对其进行近似计算。
因此,基于分数阶PIλDμ控制器的非线性分数阶主动控制的总控制律为
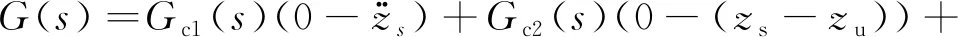
(12)
2.2 遗传算法优化分数阶PIλDμ控制器
由于遗传算法全局搜索能力较强,搜索效率较高,因此本文针对三个分数阶PIλDμ控制器共有15个未知参数需要寻优的情况,采用遗传算法进行参数寻优。遗传算法参数优化流程图如图2所示。
遗传算法参数整定步骤如下:
1) 设置种群规模为150,迭代次数为N=50,交叉概率为0.6。
2) 采用实数编码方式对种群中的个体进行编码。
3) 随机生成若干个体组成的初始种群。
4) 计算适应度函数值。
5) 通过遗传算法产生新种群。
6) 重新计算适应度函数值。
7) 判断迭代次数是否达到最大迭代次数,如果到达,则结束程序;否则返回第(4)步。
3 仿真分析
根据分数阶PIλDμ控制器设计方法,设计整数阶PID控制器,并利用MATLAB/Simulink分别建立基于分数阶PIλDμ控制器和基于整数阶PID控制器的主动控制悬架仿真模型。两种主动控制悬架和被动控制悬架的时域响应对比分别如图3~5所示,且3种悬架性能指标均方根值如表1所示。

图4 悬架动挠度时域响应对比
Fig.4 Comparison of suspension dynamicresponse in time domain
由表1可知,两种主动控制悬架分别使车身加速度降低到75.41%和80.56%、悬架动挠度增加到103.62%和108.31%、轮胎动位移降低到69.45%和79.97%。两种主动控制方式都能有效改善汽车悬架的性能,但是前者控制效果更为显著,这是因为与整数阶PID控制相比,分数阶PIλDμ控制增加了两个参数λ和μ,从而具有更为灵活的调节结构,控制效果更好。因此能够更好地抑制悬架的振动和减少路面对悬架的冲击,但是由于这3个性能指标相互制约相互影响,在改善非线性分数阶悬架舒适性时,使得悬架动变形增大。
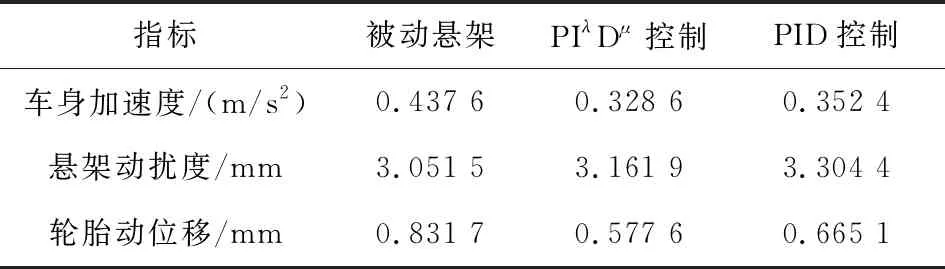
表1 3种悬架性能指标均方根值表Tab.1 Root mean square values of three suspensionperformance indexes
分数阶PIλDμ控制和整数阶PID控制的目标函数最优值随遗传代数的曲线图如图6所示。
由图6可知,在遗传优化40代之后目标函数趋于稳定,而且整个优化过程中分数阶PIλDμ控制的目标函数变化较小且目标函数值更优,因此分数阶PIλDμ在对非线性分数阶悬架进行控制时更具有优势。
4 结论
本文基于分数阶微积分理论建立了一种更能准确描述汽车悬架系统非线性及粘弹性特性的非线性分数阶悬架模型,并利用遗传算法优化设计分数阶PIλDμ控制器和整数阶PID控制器对该系统进行主动控制对比仿真研究。仿真结果表明,基于分数阶PIλDμ主动控制悬架系统的性能指标整体优于整数阶PID主动控制,从而进一步验证了非线性分数阶悬架模型的合理性和分数阶PIλDμ主动控制的有效性。
