具有集间良好互相关性的多子集无碰撞区跳频序列集
2020-12-08许成谦李伟杰
许成谦,徐 琪,李伟杰
(燕山大学 信息科学与工程学院,河北 秦皇岛 066004)
0 引言
跳频码分多址系统具有抗干扰、安全、多址等特点,在军事无线电通信、移动通信以及现代雷达和回声定位系统中有着广泛的应用。跳频序列在跳频通信系统中扮演着十分重要的角色。跳频序列的性能直接影响到跳频通信系统的性能[1-2]。在这样的系统中,每个跳频序列分配给一个用户,如果任意两个用户同时占用相同的载波频率,就会发生信号碰撞。因此,我们希望这些碰撞尽可能少发生。碰撞程度由汉明相关函数来评估。为了减少互相碰撞的干扰,无碰撞区(No-hit-zone, NHZ)跳频序列集由此被提出。无碰撞区跳频序列集的汉明相关特性在整个周期内不再要求是理想的,而只是要求序列在一定的延迟范围内有理想的汉明相关性就可以了。目前,关于无碰撞区跳频序列集的设计已有广泛的研究[3-7]。然而这些构造出的单集合无碰撞区跳频序列集只能消除同一小区用户带来的干扰,在多小区环境下,相邻小区用户信号造成的干扰难以消除。为降低小区之间用户的干扰,一个有希望的解决方案是构造的集合应包含多个子集,每个小区分配一个子集。同一小区内的干扰通过子集内序列优良的汉明自相关性与互相关性予以消除,不同小区间的干扰由子集间序列的汉明互相关性予以消除。
本文提出一种多子集NHZ跳频序列集的构造方法,基于一次碰撞的非重复跳频序列集经过移位序列交织构造出多子集NHZ跳频序列集。交织得到的序列集包含多个子集,每个子集是NHZ跳频序列集,集间具有良好的低互相关性。
1 基本概念
定义1设F={f0,f1,…,fq-1}是一个包含q个频隙的频率集合,x=(x0,x1,…,xN-1)和y=(y0,y1,…,yN-1)分别为频率集合F上的两个跳频序列,其中xi,yi∈F,i=0,1,…,N-1。跳频序列x和y的周期汉明相关函数的定义为
(1)
定义2S为F上M个长度为N的跳频序列构成的集合,若跳频序列集合S上任意序列x=(x0,x1,…,xN-1)和y=(y0,y1,…,yN-1)的周期汉明相关函数满足
(2)
则称跳频序列集S为(N,M,q,Zn)无碰撞区跳频序集,简称NHZ跳频序列集,称Zn为无碰撞区长度。
定义3对于跳频序列x=(x0,x1,…,xN-1),任意i,j∈{0,1,…,N-1},i≠j,若xi≠xj,则称序列x为无重复跳频序列。若跳频序列集S中序列都是无重复跳频序列,则称S为无重复跳频序列集。
定义4S为F上M个长度为N的无重复跳频序列集,若无重复跳频序列集合S上任意序列x=(x0,x1,…,xN-1)和y=(y0,y1,…,yN-1)的周期汉明相关函数满足
(3)
则称S为一次碰撞的无重复跳频序列集。
定义5[8]设两个跳频序列a=(a0,a1,…,aN-1)和b=(b0,b1,…,bN-1),如果对于0≤i≤N-1, 0≤τ≤N-1有ai=bi+τ成立,则称序列a和b移位等价,否则称为移位不等价。
定义6设S表示一个序列集,包含l个子集,S={S0,S1,…,Sl-1},每个子集是一个参数为(N,M,q,Zn)无碰撞区跳频序列集。若Hs(i,n),s(j,m)(τ)=δ,δ≪N,s(i,n)∈Si,s(j,m)∈Sj,0≤i,j≤l-1,i≠j,0≤n,m≤M-1, 0≤τ 设a=(a0,a1,…,aN-1)为跳频序列,ei=(ei,0,ei,1),其中ei,0,ei,1∈{0,1,…,N-1},则由序列a和序列ei可以构成一个N×2的矩阵 (4) 其中下标运算均为模N加法运算。将矩阵U中的元素按行首尾连接得到周期为2N的序列u=(u0,u1,…,u2N-1),其中u2t1+t2=at1+ei,t2,0≤t1 引理1设a=(a0,a1,…,aN-1)和b=(b0,b1,…,bN-1)为两个跳频序列,ei=(ei,0,ei,1)和ej=(ej,0,ej,1)为两个移位序列,ei,0,ei,1,ej,0,ej,1∈{0,1,…,N-1},交织序列u=I(Lei,0(a)),(Lei,1(a))和v=I(Lej,0(b),Lej,1(b)),令τ=2τ1+τ2,t=2t1+t2,0≤t1,τ1≤N-1,t2,τ2∈{0,1},则交织序列u和v的汉明互相关函数 Hu,v(τ)= (5) 如果a=b,则交织序列u和v的汉明互相关函数 Hu,v(τ)= (6) 证明令τ=2τ1+τ2,t=2t1+t2,0≤t1,τ1≤N-1,t2,τ2∈{0,1},则交织序列u和v的汉明互相关函数 Hu,v(τ)= Hab(τ1+ej,τ2-ei,0)+Hab(τ1+ej,1+τ2-ei,1)= 如果a=b,交织序列u和v的汉明互相关函数 引理得证。 引理2[10]设E={ei|0≤i 2)ei,ej∈E,ei≠ej时,有d0≠d1且d2≠d3, 其中,d0=ei,0-ej,0,d1=ei,1-ej,1,d2=ei,0-ej,1,d3=ei,1-ej,0-1,均为模N运算,则移位序列ei和ej是移位不等价的。 引理3[10]设a为基序列,ei=(ei,0,ei,1)和ej=(ej,0,ej,1)为移位序列,u=I(Lei,0(a),Lei,1(a)),v=I(Lej,0(a),Lej,1(a)),若移位序列ei和ej是移位不等价的,则交织序列u和v是移位不等价的。 引理4设a为频隙集{0,1,…,N-1}上长度为N的无重复跳频序列,E={ei|0≤i 2)对于任意ei≠ej∈E,有d0≠d1,且d2≠d3,其中d0,d1,d2,d3见引理2; 则序列集S={I(Lei,0(a),Lei,1(a))|0≤i 证明显然序列集S中序列长度为2N,序列个数为M,频隙个数为N。 下面证明无碰撞区长度为Zn。设u=I(Lei,0(a),Lei,1(a)),v=I(Lej,0(a),Lej,1(a)),τ=2τ1+τ2,t=2t1+t2,0≤t1,τ1≤N-1,t2,τ2∈ {0,1}。 由引理1可得u的汉明自相关函数Hu(τ), Hu(τ)= 综上所述,序列集S中任意序列u的自相关函数有无碰撞区(0,Zn],即碰撞区长度为Zn。 由引理1可得u和v的汉明互相关函数 综上所述,序列集S中任意两个序列u和v的互相关函数有无碰撞区[0,Zn],即碰撞区长度为Zn。 由引理2和引理3可知,序列u和v是移位不等价的。 引理得证。 引理5[11]令F是频隙数为q的频隙集,S为F上M个长度为N的跳频序列构成的集合,Zn是序列集S的无碰撞区长度,则 (7) 使得上式等式成立的跳频序列集称为最优无碰撞区跳频序列集。 构造方法1: 步骤1:选取一个F上频隙大小为q的l个长度为N的一次碰撞无重复跳频序列集A。 步骤2:取Zn为正整数,1 ej=(ej,0,ej,1)= (8) 1)当(Zn+1)整除N时, ej=(ej,0,ej,1)= (9) 2)当(Zn+1)不整除N时, ej=(ej,0,ej,1)= 步骤3:取序列集A中的序列为基序列,序列集E中的序列为移位序列构成交织跳频序列集,构造的跳频序列集如下, Si={I(Lej,0(ai),Lej,1(ai))|ai∈A,ei=(ej,0,ej,1)∈E,0≤j S={Si|0≤i 定理1构造方法1中构造的多子集跳频序列集S中的子集Si为参数为(2N,M,N,Zn)的最优无碰撞区跳频序列集,Si中序列是移位不等价的,0≤i 证明由步骤2构造移位序列集E知,对任意的ei,ej∈E均满足以下3个条件: 2)对于任意ei≠ej∈E,有d0≠d1,且d2≠d3,其中d0,d1,d2,d3见引理2; 由引理2可知,构造的E={ei=(ei,0,ei,1)|0≤i 由引理4知,序列集Si为参数为(2N,M,N,Zn)的无碰撞区跳频序列集,并且序列集Si中任意两个序列是移位不等价的。 由引理5知,序列集Si是最优的。 对于s(i,n)∈Si,s(j,m)∈Sj,τ=2τ1+τ2,0≤τ1 Hs(i,n),s(j,m)(τ)=2Hab(τ1)=2。 同理,当0≤τ<2N,τ2=1时,0≤τ1≤N-1,可得 Hs(i,n),s(j,m)(τ)=2Hab(τ1)=2。 综上所述,子集间的汉明相关值为2。 例1选取参数为(7,6,7,1)一次碰撞非重复跳频序列集A,其中 a0=(0,1,2,3,4,5,6), a1=(0,2,4,6,1,3,5), a2=(0,3,6,2,5,1,4), a3=(0,4,1,5,2,6,3), a4=(0,5,3,1,6,4,2), a5=(0,6,5,4,3,2,1)。 e0=(0,6),e1=(4,2)。 以ai作为基序列,利用交织理论可得包含6个子集的序列集合S={S0,S1,S2,S3,S4,S5},如下: S0={s(0,0)=(0,6,1,0,2,1,3,2,4,3,5,4,6,5), s(0,1)=(4,2,5,3,6,4,0,5,1,6,2,0,3,1)}, S1={s(1,0)=(0,5,2,0,4,2,6,4,1,6,3,1,5,3), s(1,1)=(1,4,3,6,5,1,0,3,2,5,4,0,6,2)}, S2={s(2,0)=(0,4,3,0,6,3,2,6,5,2,1,5,4,1), s(2,1)=(5,6,1,2,4,5,0,1,3,4,6,0,2,3)}, S3={s(3,0)=(0,3,4,0,1,4,5,1,2,5,6,2,3,6), s(3,1)=(2,1,6,5,3,2,0,6,4,3,1,0,5,4)}, S4={s(4,0)=(0,2,5,0,3,5,1,3,6,1,4,6,2,4), s(4,1)=(6,3,4,1,2,6,0,4,5,2,3,0,1,5)}, S5={s(5,0)=(0,1,6,0,5,6,4,5,3,4,2,3,1,2), s(5,1)=(3,5,2,4,1,3,0,2,6,1,5,0,4,6)}。 通过计算,每个子集内的汉明相关函数值如下: Hs(i,0),s(i,0)(τ)= Hs(i,1),s(i,1)(τ)= (14,0,0,0,0,7,0,0,0,7,0,0,0,0), Hs(i,0),s(i,1)(τ)= (0,0,0,7,0,0,7,0,7,0,0,7,0,0)。 子集间的汉明相关函数值如下: Hs(i,0),s(j,0)(τ)= (2,2,2,2,2,2,2,2,2,2,2,2,2,2), Hs(i,0),s(j,1)(τ)= (2,2,2,2,2,2,2,2,2,2,2,2,2,2), Hs(i,1),s(j,0)(τ)= (2,2,2,2,2,2,2,2,2,2,2,2,2,2), Hs(i,1),s(j,1)(τ)= (2,2,2,2,2,2,2,2,2,2,2,2,2,2)。 本文提出了具有集间低互相关多子集无碰撞区跳频序列集的概念,通过一次碰撞的非重复序列集和不等价的移位序列交织得到了多个最优的无碰撞区跳频序列集,无碰撞区长度在满足一定条件下可灵活选取,其集合间具有优良的汉明互相关性。构造出的多子集可以应用到多个小区间环境中,降低了小区间用户干扰。

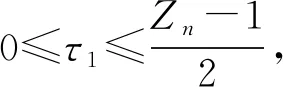

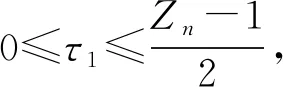
2 多子集跳频序列集的构造
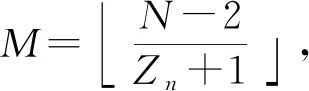



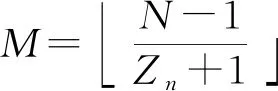
3 构造实例

(14,0,0,7,0,0,0,0,0,0,0,7,0,0),
4 结论
