硅掺杂对InAs/GaSb II类超晶格磁输运的影响
2020-12-08应志超宋志勇陈爱英康世雄
应志超,宋志勇,陈爱英,林 铁,康世雄
(1.上海理工大学 材料科学与工程学院,上海 200093;2.中国科学院 上海技术物理研究所 红外物理国家重点实验室,上海 200083;3.华东师范大学 极化材料与器件教育部重点实验室,上海 200063)
引言
红外探测器历来是军事、航天、安全领域热门的精密器件,红外探测器的精度也在随着应用环境的升级而不断提升,同时也促进了对红外探测器内部核心材料的研究。20世纪80年代,Smith等[1]首次提出InAs和GaSb组成的第二类超晶格材料具有截获长波红外的能力,这种长波红外超晶格由于在晶胞中添加了一层或多层InSb,使得其晶格中的有效代隙能可以被调整,同时通过改变InAs层的厚度可以调控超晶格截取红外线的波长值,这些特性使得InAs/GaSbⅡ类超晶格作为长波红外探测最有潜力的材料而被广泛研究[1]。
InAs/GaSbⅡ类超晶格属于III-V族的窄禁带半导体材料,作为红外探测器件的核心材料,其光电性能的强弱是一个主要的影响因素,因此也引起了人们对于InAs/GaSbⅡ类超晶格生长工艺的关注,这是因为不同的工艺带来的光电性能不同。目前普遍使用的是分子束外延法生长InAs/GaSb,分子束外延法最早是由20世纪90年代美国休斯顿研究实验室的科学家用来在GaAs衬底上生长InAs/GaSbⅡ类超晶格[2-3],此后其他科学家利用这种生长方法获得了高质量的InAs/GaSbⅡ类超晶格,并且逐步提升了其截取长波红外的波长值[4-6]。但对于超晶格材料的生产成本一直居高不下的问题,使得我们需要尽快寻找一种替代性的生长方法。金属有机化学气相沉积(MOCVD)是一种新兴的超晶格生长方法,它可以显著降低超晶格材料的生产成本。已有研究人员通过MOCVD方法使InAs衬底和拉伸应变GaAs型界面层巧妙的生长出了InAs/GaSbⅡ类超晶格材料[7-8],与以往的GaSb衬底和InSb型界面层相比,这种方法更能控制砷的残留和阴离子的交换。
此外,对于提升超晶格材料的光电性能,掺杂往往也是选择较多的一种方法,而不同的掺杂带来不一样的性能改变,以及p型和n型的掺杂形式会对材料有很大程度的影响。同时对于InAs/GaSbⅡ类超晶格光电性能的检测方面,一贯采用弱局域效应与半导体导电性能之间的关系来衡量。Herling等[9]在InAs/GaSb量子阱中通过磁输运测量观察到了反弱局域效应,并运用温度和栅极来调控样品的磁阻,解释了主要的自旋轨道弛豫机制是Elliott-Yafet(EY)机制,而不是之前提出的Dyakonov-Perel(DP)机制。对于在InAs/GaSb超晶格中的弱局域效应还很少有人报道。因此,本文采用了MOCVD生长技术和n型重掺杂的方式在InAs衬底上生长InAs/GaSb超晶格材料,并利用低温电学测量方法系统研究了该超晶格材料的磁输运性质。
1 实 验
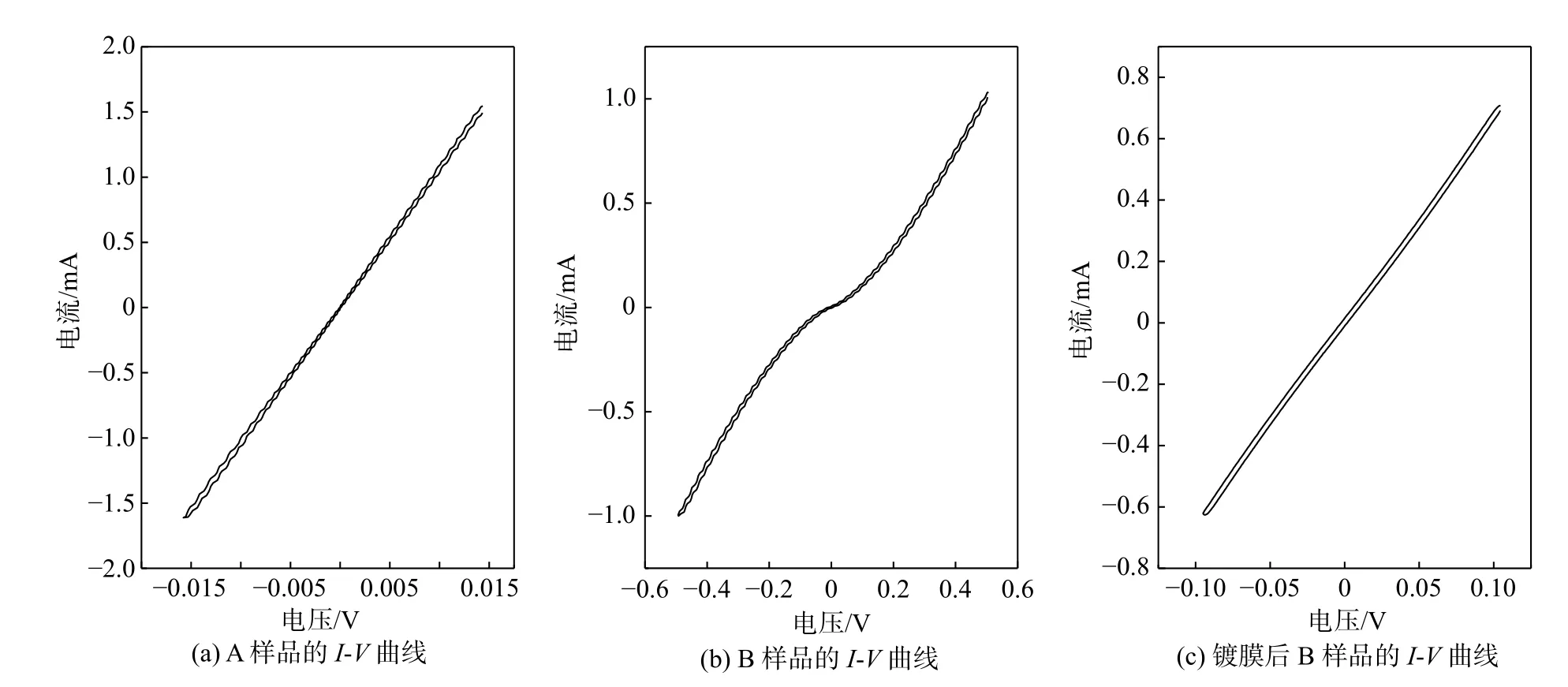
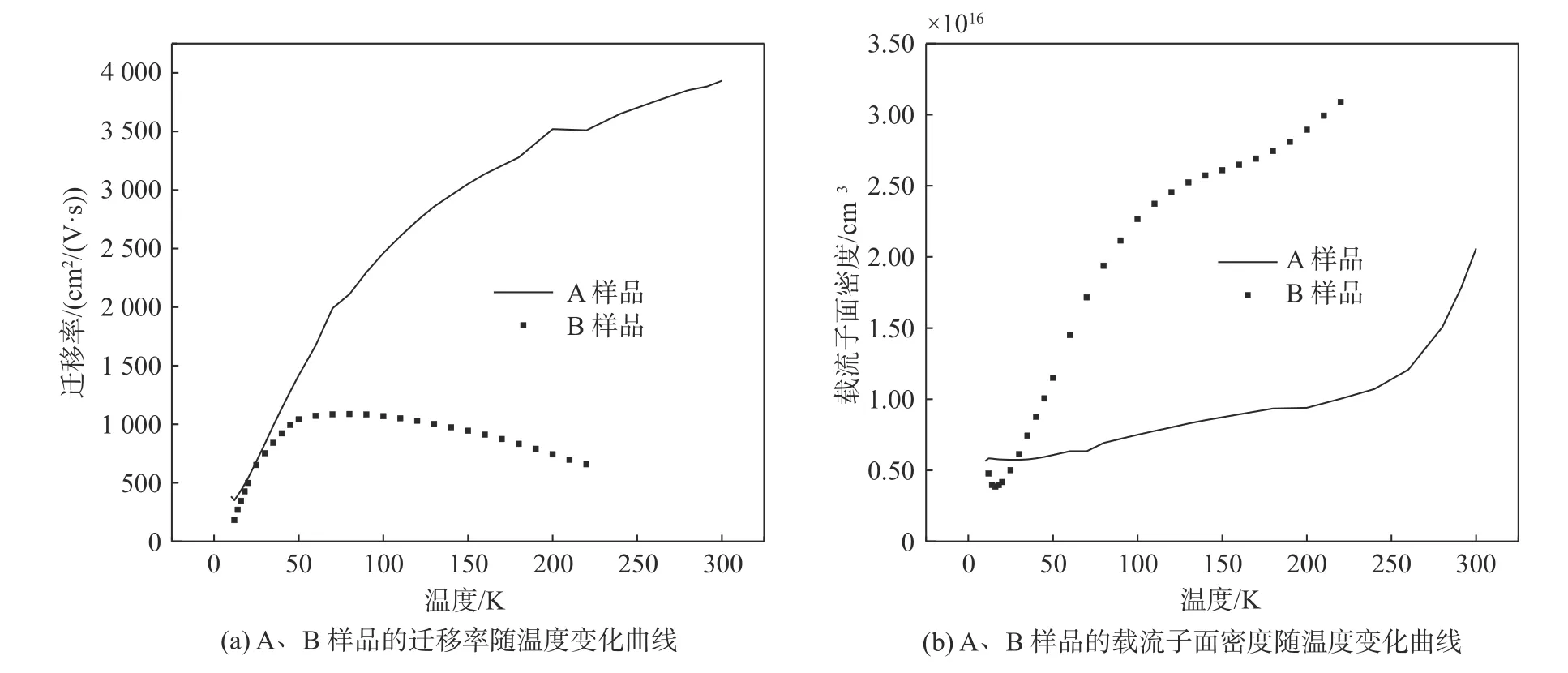
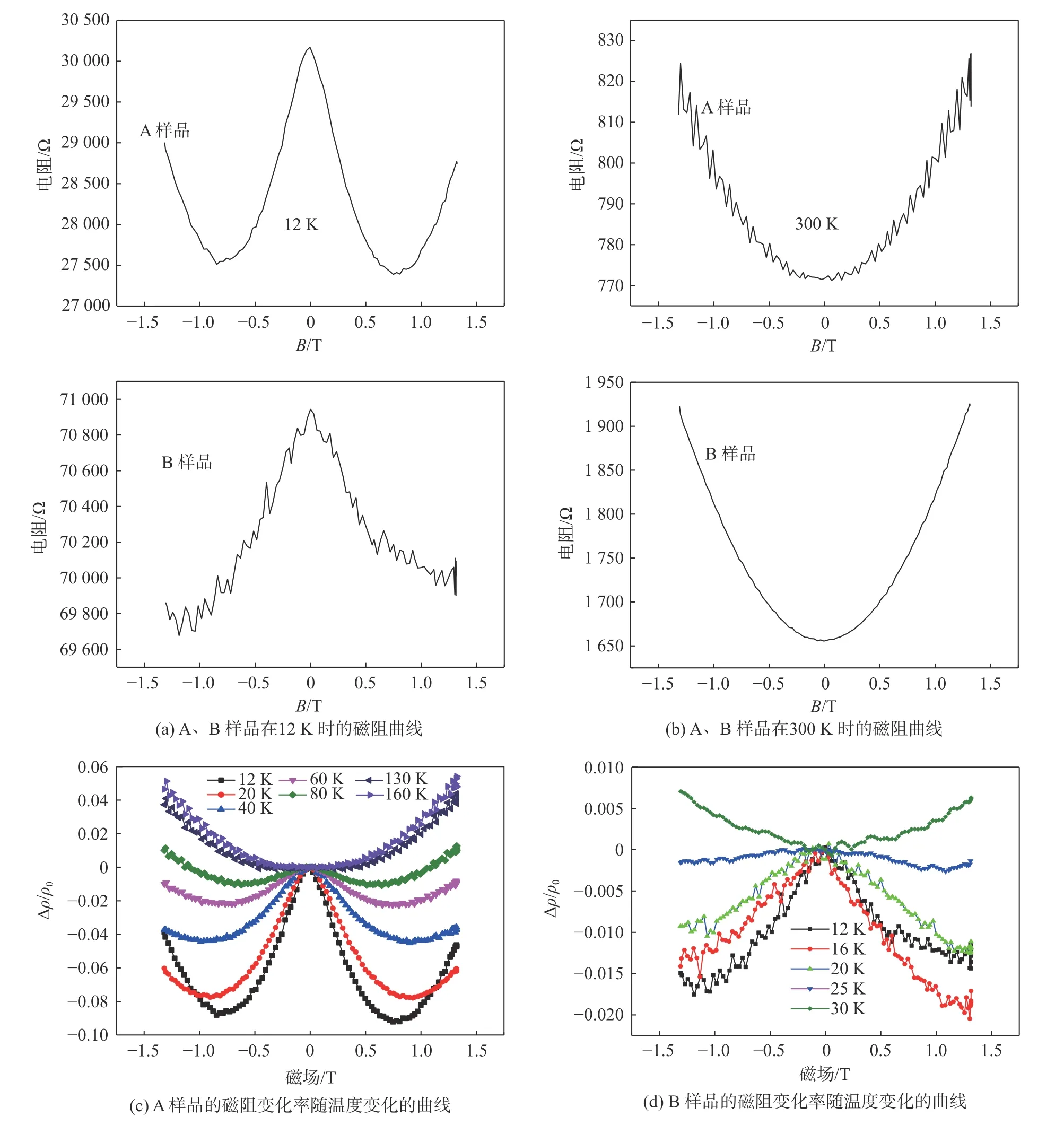
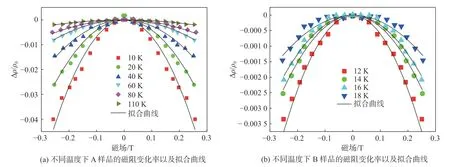
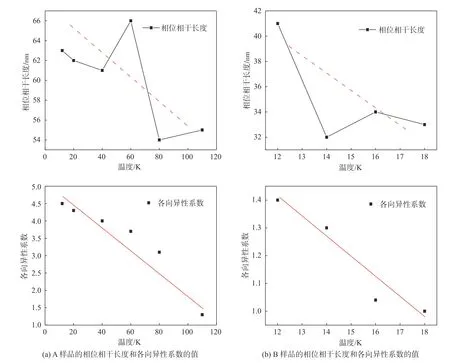
利用化学有机气相沉积方法(metalorganic chemical vapor deposition)在半绝缘的InAs(001)衬底上生长了两块InAs/GaSb超晶格薄膜,分别记为A和B。两块样品的超晶格周期厚度均为4.2 nm,其中InAs层厚度为1.8 nm,GaSb层厚度为2.4 nm。A样品中掺杂了大量的硅(掺杂硅原子的个数为2.0*1016cm−3),其生长速率为100 μmol/min,B样品不做掺杂。将两块材料裁取成0.8 cm*0.8 cm的正方形,在其四个角上采用焊铟的方法制作电极,并将其置于垂直磁场下(−1.4 T 安特性曲线。A样品I-V曲线呈线性,表明A样品与铟之间形成了良好的欧姆接触。而B样品的I-V曲线为非线性关系,当电流通过时,接触点间的电压降大于样品本身的电压降,样品与铟之间形成了势垒,图1(a)表明经Si掺杂后的n型InAs/GaSb超晶格更易形成欧姆接触,可能的原因是掺杂的浓度高,使得势垒区的宽度变得很薄,由于隧道效应的作用,电子贯穿势垒形成了巨大的隧道电流,从而使得它的接触电阻很小,相对更容易作欧姆接触。 图1展示了A、B样品在12 K温度下的伏 图1 样品A、B在12 K下的伏安特性曲线Fig.1 I-V characteristic curves of samples A and B at 12 K 为此,我们用双离子束缚技术在B样品的四角上制作了100 nm厚的AuGeNi[10],然后经过300 ℃左右的低温退火使其形成欧姆接触。测得的I-V结果如图1(c)所示。结果表明B样品实现了欧姆接触。 图2分别给出了A、B样品在0磁场下的迁移率μ以及载流子二维密度随温度T的变化关系。 图2(a)中A样品的迁移率随温度的升高而增加,呈现了半导体的典型特点。而B样品则相对特殊,其迁移率随温度的升高,先增加后减小,在75 K附近,迁移率达到最大值1 088 cm2/(V·s)。这种变化主要归因于[11]主导散射机制的转变,即在温度低于75 K时,杂质散射主导了B样品的散射机制,而当温度高于75 K时,主要的散射机制则为声子散射。图2(b)中,两个样品的载流子浓度均随温度的升高而增加。其中A样品的温度大于200 K时,载流子浓度增加的尤为明显,因为从价带到导带的热激发使得InAs/GaSb的体载流子浓度和温度的关系成为主导。对于B样品,在220 K温度以下其为p型半导体,220 K温度以上时,由p型半导体逐渐转变成n型半导体,且通过迁移率谱算得有两种载流子均对电导做了贡献。本文对多种载流子问题不做过多解释,我们将在以后的研究中给予说明。 为了进一步研究Si掺杂对InAs/GaSb超晶格的电输运性质的影响,我们分别对两个样品进行了磁阻测试。图3(a)分别给出了12 K时A、B两个样品的方块电阻R□随磁场变化的磁阻曲线。 图2 样品A、B零场下的迁移率和载流子面密度随温度的变化曲线Fig.2 Mobility and carrier surface density vs.temperature of samples A and B at zero field 由图3(a)可知,温度在300 K时,A、B两个样品的R□随磁场的变化表现为抛物线型,即方块电阻R□的变化值与磁场强度的平方成正比,表达式为:R□(A或B)−R□(0)=ΔR□(A或B)∝B2[12],我们可以用半经典机制来解释电阻与磁场所呈现的抛物线型:在垂直磁场的作用下,半导体中电子受洛伦兹力而发生偏转,导致沿电场方向的电流密度有所降低,即由于磁场的存在,半导体的电阻增大。由图3(b)可知,在极低温下(T=12 K),半经典机制已经不能解释其磁阻曲线的变化。具体来说,A和B样品均表现出了弱局域效应[13](weak localization,WL)。载流子在输运过程中会不断地受到不同类型的散射,一般有弹性散射和非弹性散射两种,由载流子与杂质原子发生碰撞的弹性散射使得在闭合轨道中两种方向相反的电子波发生干涉,结果是不断干涉的电子波函数的相位将叠加,导致干涉增强,从而增大了电阻,此即为弱局域效应。而电子与声子和电子与电子之间发生的非弹性散射则会破坏相位相干性,若考虑自旋轨道耦合效应(spin-orbit interaction,SOI),在闭合轨道的两列方向相反的电子波自旋方向的变化导致了相位变化,原本干涉增强的两列电子波反而减弱,从而减小了电阻,此即为反弱局域效应(weak antilocalization,WAL)。 图3(b)中,在12 K的低温下,A、B样品R□都表现为WL,即存在一个“尖包”,随磁场的增大,方块电阻反而减小,在0磁场附近出现负磁阻,这就是所谓的WL。为了进一步探究温度对WL的影响,对A、B两个样品分别进行了变温磁阻测量。图3(c)、(d)分别给出了A、B样品的磁阻曲线与温度的关系。由图3(c)可知,A样品温度在130 K以下,磁场范围在−0.5~0.5 T时,电阻随磁场的升高而减小,由于弱局域效应而表现为负磁阻。负磁阻对温度具有很高的依赖性,随着温度从12 K升高到80 K,负磁阻逐渐减小,温度达到160 K时,负磁阻消失,A样品的磁阻曲线呈现为半经典机制B2。这种结果表明温度对弱局域效应具备调控的能力,因为当温度升高时,系统中的非弹性散射时间(inelastic scattering time)变短,相比于弹性散射时间在低温下的主导作用,其在高温下逐渐占据主导地位,从而破坏了相位相干性,弱局域效应也随之消失,也可以说是热效应抑制了量子局域化。从图3(d)中,未掺杂的B样品其弱局域效应也和A样品类似,但是温度对WL的影响却不同,其在30 K时,弱局域效应消失。对比图3(c)、(d)可知,B样品的WL对于温度更加敏感。反之,经Si掺杂的A样品相比于B样品来说,能在大范围的温度下保持弱局域效应。在12~300 K的温度下,我们并没有观察到反弱局域效应,这也表明该样品的自旋轨道散射时间要大于其弹性散射时间。 图3 A、B样品的磁阻以及磁阻变化率随温度变化的曲线Fig.3 Curves of the magnetoresistance and the rate of change of magnetoresistance of samples A and B as a function of temperature 对于A、B样品在低温下的WL磁阻曲线,可以用Kawabata模型[14]来拟合。其模型为: 式中:r是样品A,B的电阻;e是基本电荷;ħ是约化普朗克常量;B是磁场强度;是电阻的变化率;α是有效质量的各项异性系数,mz和m//分别是有效质量垂直于样品层和平行于样品层的分量,α可以用来表示一个系统的二维和三维的性质,当系统为纯三维时,α=1,当系统为纯二维时,α则为无穷大,即α值的大小代表了系统各向异性的大小;F(x)是赫尔维茨函数(Hurwitz zeta function),即为 式中x是一个无量纲的参数,可表示为x=τ是非弹性散射时间,D为扩散系数,Lφ为相位相干长度。我们通过改变α和Lφ来对磁阻曲线(−0.3 T 图4 在各温度下(磁场为−0.3 T 同时,由式(1)、(2)可得如图5所示A、B样品的Lφ和α随温度的变化关系。 由图5(a)、(b)可知,A、B样品的相位相干长度Lφ均随温度的升高而下降,这就很好的解释了高温下,弱局域效应消失的原因,即热效应抑制了量子局域化。然而A和B的Lφ在各温度下相差甚远。Si掺杂的A样品的Lφ比未掺杂的B样品要高得多,我们认为这是由于A样品经硅调制掺杂后,高掺杂的n型层GaSb中的电子将转移到InAs的导带中,使得InAs的电离散射中心很少,因此A样品的迁移率比B样品高,A样品中带电杂质并没有被大量过滤,从而导致A样品的弹性散射时间相比于B来说更短,其相位相干性也越强。这种经过调制掺杂使得迁移率升高的方法是超晶格材料中的特性,为研制高速低功耗器件提供了有力的可行性。对于掺杂量和材料物理性能的关系,Lv等[15]在InAs/GaAs量子点中掺杂了不同浓度的硅,光致发光光谱表明InAs/GaAs量子点的光致发光强度随掺杂浓度的升高先增后降,其原因是由于掺杂的硅原子有效地抑制了量子点附近的非辐射复合区域,因此改善了量子点的光学特性,多余的电子会进入量子点的导带,提高其载流子浓度。Dhifallah等[16]也通过在GaAs/AlGaAs中掺杂不同浓度的硅得到了相似的结论。对于InAs/GaSb二类超晶格来说,由于重掺杂硅的作用,其迁移率首先会上涨,但是掺杂的量过大时,其载流子浓度会上升,会加大离化杂质对电子的散射,从而降低了迁移率,这不利于研制高速低功耗器件。然而对于最合适的硅原子掺杂浓度,我们需要由后续的试验证明。 由图5(a)、(b)可知,A、B样品的各向异性系数α均随温度的升高而下降。对于B样品,各向异性系数α参数由12 K时的1.2下降到18 K时的1.0,变化并不大,可见B样品中的系统并无各向异性。而A样品的α值在12 K时达到了4.5,在110 K左右趋向于1.0,表明温度越低,其各向异性越明显,若α的值达到19时,此时系统处于三维与二维之间,Kawabata模型就不能用来拟合弱局域效应,需要另外的模型来作运算,如Hikami-Larkin-Nagaoka(HLN)模型。因此,由α的值可知,三维的Kawabata模型均适用于A、B两个样品。 图5 A样品和B样品的相位相干长度Lφ和各向异性系数α随温度的变化曲线Fig.5 Phase coherence length and anisotropy coefficient of samples A and B as a function of temperature 本文对MOCVD生长的调制掺杂硅的InAs/GaSb二类超晶格磁输运性质做了系统的研究。实验发现调制掺杂n型硅加大了InAs/GaSb二类超晶格迁移率。磁阻测量的结果显示其在低温下均有弱局域效应,且经过重掺杂的A样品,能在更高的温度下保持WL,表明其更不易受到热效应的影响,显现出良好的稳定性。基于Kawabata模型的分析表明,硅的重掺杂提高了InAs/GaSb的相位相干长度,使其表现出更优异的物理性能。2 结果与讨论
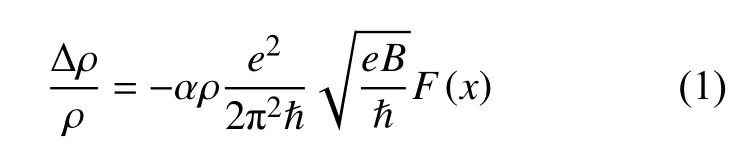

3 结论
