向学习深处的漫溯

【摘要】深度学习是对学习状态的质性描述，涉及学习的投入程度、思维层次和认知体验等诸多层面。学习者通过思考、探究、推理、反思等深度学习过程的直接和间接的学习体验与感悟，能在学科概念层面思考问题，形成合理的知识结构与独到的见解。课前研就是以“深入研究教材、建构认知结构”为基础，以引导学生“深度加工知识”为核心;是以“深度课堂教学”成全“深度学习”状态，提升核心素养的前期准备。

【关键词】深度学习 课前研 教材 案例

一、深度学习的理解

学习的本质是什么？学习，是一个整合知识与改变思维的过程（学与用），学习就是对联结进行重新组织。课堂教学本质是指通过课堂的教学实现教与学的统一，从而达到目的，根本体现为教师的教与学生的学。

什么是深度学习？

与浅层学习（以单纯的知识获取与记忆为主要特征）相比，深度学习是一种以高阶思维为主要认知活动的持续性学习过程，是对学习状态的质性描述，涉及学习的投入程度、思维层次和认知体验等诸多层面，强调对知识本质的理解和对学习内容的批判性利用，追求有效的学习迁移和真实问题的解决，具有高投入性和建构性的内涵特质。深度学习状态的形成离不开学习者的学科背景，学习者通过思考、探究、推理、反思等深度学习过程的直接和间接的学习体验与感悟，形成科学的知识结构、专业智慧和解决问题的实际能力就形成了核心素养。

计算机领域的深度学习，让我们体会到学习规则不是最重要的，我们的教学就是要引导学生从学习原理转向学会思辨，转向理解与批判、联系与构建、迁移与应用。实现深度学习的关键在哪里？——深度教学，是对儿童特点、学科本质理解、把握基础的教学。深度学习的路径就是找到适合儿童的数学学习路径，课堂教学最重要的载体是教材。深度学习，首要是教师深度思考教材，其次深度研究学生，然后才是在具体学习中，通过教师引导、学生主动投入，深入理解、建构、迁移的学习过程。

二、课前研的解读

课前研：以“深入研究教材、建构认知结构”为基础，以引导学生“深度加工知识”为核心，是以“深度课堂教学”成全“深度学习”状态，提升核心素养为目的的前期准备。 主要涉及学情分析（找学生认知起点）、教材知识分析（探求学科知识本质）、 内容联结分析（知识结构）、教学活动设计（设计促进深度学习的活动及引领活动的问题）等。

（一）数学学科的本质

对基本数学概念的理解、对数学思想方法的把握、对数学特有思维方式的感悟、对数学美的鉴赏、对数学精神（理性精神与探究精神）的追求。

学习数学是为了什么？不仅是掌握算术法则、计算技巧与基本的数理知识，更重要的是通过研究符号与数字的关系，理解数字背后的概念，掌握相关理论法则，形成演绎推理、归纳推理和类比推理等思维方式或数学思想，并用以理解和解释相关现象与关系、解决和处理现实生活中的具体问题。

基于以上所述，就明白了课前研研什么。

研教材：学科知识的本质、来源，从哪里来，到哪里去;知识的逻辑、结构。

研学生：认知学情（元认知）、认知障碍、认知困惑（问题）、怎样建立知识间的联结、构建科学的认知结构。

研学习活动设计：重点在于精心设计问题情境和学习任务，引发学生认知冲突，组织深度探究。

（二）深度研究教材的原因

课堂教学最重要的载体是教材，教材呈现给学生的是高度简化的事实观点，而几乎没有洞察收集信息和提炼事实的方法。教材很少能够告诉学生原创工作是多么的丰富并且令人兴奋。

研究表明，几乎所有的学生，甚至那些最优秀的、最聪明的学生，在理解课本中所讲到的观点时都存在困难。然而，大多教材都没有在活动和问题中思考这些障碍。

虽然大部分的教材中都含有大量的插图，但这些表征很难起到帮助作用，因为它们要么太抽象，要么过分复杂或解释不充分。

（三）课前研要关注哪些点

不同类型的学习结果需要不同类型的学习条件。比较科学的做法是依据学习的结果界定目标，从知识分类入手，依据认识论的一般规律和数学方法论的基本原理，对有关知识的产生过程进行科学的、合适的思维模拟，根据实际学情设计出切实可行的学习方案。

1.学生认知规律与认知障碍是什么？ （了解学生的什么？）

2.什么样的内容更有价值？（教什么更有利于学生核心素养的发展？）

3.什么目标更有意义？（学生应学会什么？什么核心素养獲得了发展？）

4.什么活动更有利于教与学？（如何组织教学活动能够使得学生获得真正意义的学习？）

5.如何检验学生达成了目标？ （怎么评？评什么？）

三、课前研——深度解读教材案例

在数学教学过程中，只要教师认真研究教材，能从知识的整体结构上去考虑具体课堂教学的结构，那么是可以在教学中帮助学生建立起结构性知识的，有时甚至可以用一个问题就把有关的知识联系起来。

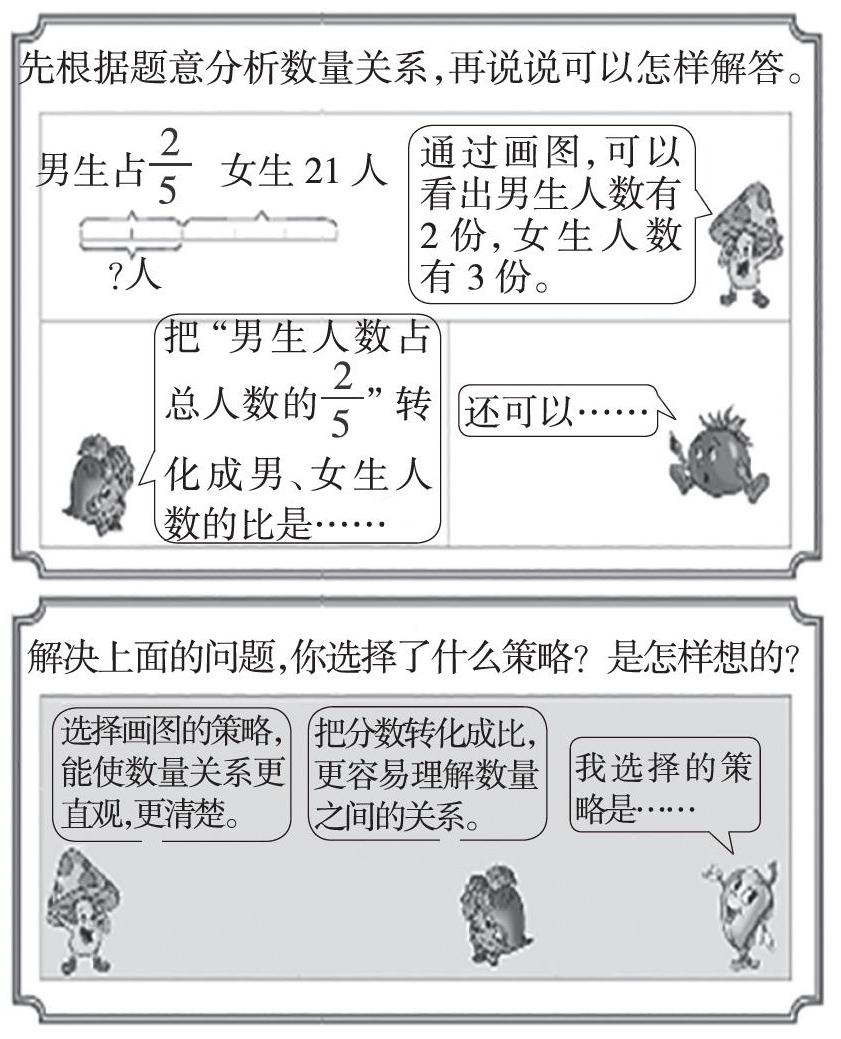
[案例一：“解决问题的策略”]

这种课基本上是这样一种局面：“所有孩子都会做，我们讲了半天，都没人理我！”学生都已经会解决问题了，那么课堂上到底要干什么？

我们课堂上要把精力真正投入去捕捉、发现、提炼“精华”上（这个精华来自课前研的发现），这里的“精华”指的就是数量关系。解决问题的核心其实就是找到数量间的相等关系，画图等策略是为找到新的等量关系服务的。

题中有两个未知量，两个数量关系，不论根据哪个数量关系，都不能直接列式解答。男生人数（？）+女生人数（21）=总人数、总人数×=男生人数。学生以前的经验是对于“总人数×=男生人数”这样的数量关系，一般是知道其中的两个求第三个，这道题目中只知道男生人数与总人数的关系，男生人数与总人数均未知，这个关系与已知的21之间没有关联。因此必须有一种策略，把面临的新问题转化为以前的“知二求一”的数量关系，将两个未知量转化成一个未知量。抓住学生对数量关系的理解，切实激活学生寻求策略的“生长点”。或者转化为女生人数与总人数之间的关系，利用21求解总数，然后得出男生人数;或者转化为男生与女生人数之间的关系，直接利用21求得男生人数。这就是这节课的策略，转化数量关系。

[案例二：“求两数相差多少的实际问题”]

以苏教版数学一年级下册第四单元例7为例，本册第一单元是20以内退位减法，那么，本节课教学的落脚点在哪里？显然不是退位减法怎么算的问题，而是怎样列式、列什么样的算式的问题。儿童学数学是从语言开始的，此前对于减法的经验是知道“去掉用减法”，多数的表象是从整体之中去掉部分，求剩下的部分。而这个问题，是两个数量作比较，学完这节课后，学生在认知上就是要把“比多、比少”与用减法（大减小）相匹配，在以后的问题中知道比较大小要用减法。学生在学习这节课之前还有一个很有用的认知经验：已经学会用数来判断相等、多、少。那么这节课怎样实现由“去掉”到“比多、比少”的跨越呢？我们再来看教材59页主题图，红花和蓝花对应地放在一起，这种对应不就能实现：去掉同样多的，留下不同样多的，这样大小的比较就衔接上以前的“去掉”用减了吗？基于对教材的深度解读，我们的课前研就能这样确定这节课的学情、目标及问题引领的活动。

认知学情分析：1.学生已经学会用数来判断相等、多、少。2.学生已经学会100以内减法的计算方法并且形成了计算技能。

学习目标：学会多多少或少多少的计算算式。

过程中的问题引领：

男生抓的红色花片和女生抓的蓝色花片各是多少？——（男生抓了13个红色花片，女生抓了8个蓝色花片。数量的表达）→红色花片多还是蓝色花片多？——（红色花片多。用数判断多与少）→为什么红色花片多？——（13比8大。用数比大小）→多少个红色花片和蓝色花片一样多？——（8个。从多的里面找小的，确定相同部分）→去掉8个红色花片，男生多抓了多少个红色花片？——13-8=5个。（勾起原有经验“去掉”用减）→红色花片比蓝色花片多多少个？——（13-8=5个。自然过渡到比多用减问题）→藍色花片多少个和红色花片一样多？——（13个。再次反向理解同样多）→现在去掉8个蓝色花片，蓝色花片还少多少个？——（13-8=5。多与少的对称理解）→蓝色花片比红色花片少多少个？——（13-8=5个。比多用减，比少也用减，学生明白比多少要用减）。

在深刻研究教材的基础上，将知识纳入知识体系，使学到的知识具有清晰的内部结构性，使知识之间建立本质联系，在知识的内在联系中体现出数学思想和方法的强大作用，是培养学生的数学头脑、提高学生的数学素养的重要途径。

四、促进课堂深度学习的有效教学途径

以概念教学为例：

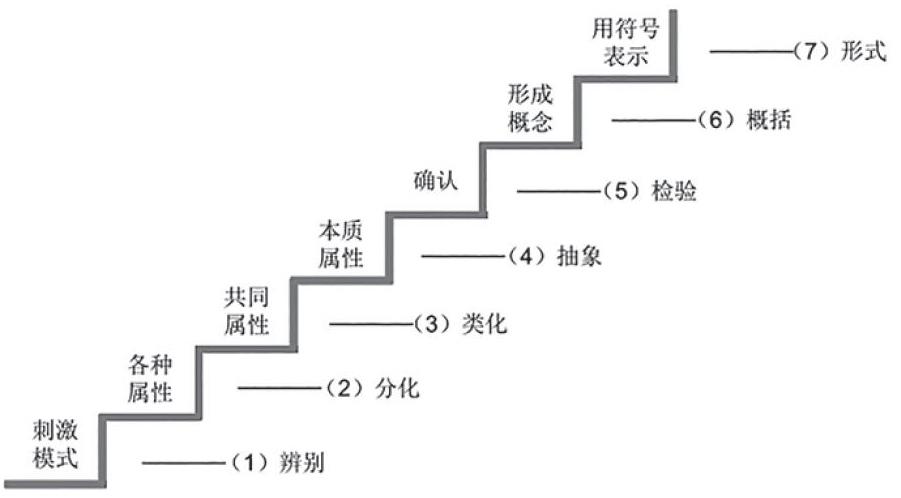
了解概念形成的过程，即可把握住儿童认知与思维的过程。概念形成的一般过程是这样界定的（如图）：

数学的概念、数学方法与数学思想的起源与发展都是自然的。从课堂教学的要求看，概念教学的自然包括两方面：一是知识的逻辑顺序自然;二是学生的心理逻辑自然，主要是思维过程自然。“自然的概念教学过程”是上述两方面的融合。“让学生参与概念的概括活动中”，不轻易打断学生的思维和活动，适时地“以问题引导学习”，在“追问（质疑）——反思”的过程中深化概念的理解，使概念的理解成为学生自己主动思维的结果。显然这是让学生经历概念的创生与发展、建立的过程，在活动中体验、理解。学生要理解一个数学概念，就必须围绕这个概念逐步建立一个概念网络，这个网络越丰富越复杂，这个学生的理解也就越深刻。

判断学生对某个概念是否理解的证据应该包括以下几个方面：

感知：指学生对这个概念的认识与信念。

表征：指学生对概念的描述和表示，其中包括书面的、图形的、表格的和口头的。

联结：指学生在概念的各种表征之间建立联系，理解的程度就取决于联结的数量与强度。

应用：指学生运用这个概念去解决问题。

途径：测试、问卷、访谈、出声思维等，也可以画概念图。

深度学习是发展学生核心素养的有效途径。深度学习过程着眼于学生对所学内容的整体理解，促进学生的知识建构和方法迁移，并有助于学生高阶思维的发展，让学生在解决问题的过程中提高核心素养。我们可以从以下策略中找到促进课堂深度学习的有效教学途径：经历思维过程，让深度学习真正发生;设计问题化学习，通过活动多维体验，让深度学习真正发生;强化拓展性学习，学科整合让数学深度学习真正发生;开展主题性学习，设计学科核心问题，促进学生深度学习。

【参考文献】

[1]王天蓉，徐谊. 有效学习设计：问题化、图示化、信息化[M]. 北京：教育科学出版社，2010.

[2]康淑敏. 基于学科素养培育的深度学习研究[J]. 教育研究，2016（7）.

[3]张桂芝.小学数学“深度学习”的思考与实践[J].教育视界，2019（16）.

[4]郭华.深度学习及其意义[J].课程·教材·教法，2016（11）.

注：本文系山西省教育科学“十三五”规划2019年度正高级教师和特级教师专项课题，特级教师孙晓红的“体验学科文化的小学数学深度学习研究”成果之一，课题编号：TJZX-19021。