兰新线铁路轨道几何状态劣化短期预测模型研究

常艳艳，刘仍奎，王福田，陈云峰

(1.北京交通大学 轨道交通控制与安全国家重点实验室，北京 100044；2.北京交通大学 交通运输学院，北京 100044；3.中国铁路兰州局集团有限公司 工务部，甘肃 兰州 730000)

受运输组织、地理环境等因素的影响，兰新线轨道不平顺状态变化较快，捣固周期较短，管理者需要对线路质量变化做出快速响应。以捣固作业为例，中国铁路兰州局集团有限公司管辖的兰新线长度为985.5 km，该段线路每年捣固一遍，重点地段甚至捣固两遍，捣固工作量大。国内外许多学者对铁路轨道几何状态劣化规律建模问题进行过研究，这些模型可以分为确定性模型[1]、随机性模型[1]和机器学习类模型。

确定性模型是指利用回归分析方法以及轨道几何状态历史检测数据，建立轨道几何状态与运行时间或通过总重之间的函数关系，通过确定的函数关系来预测轨道几何劣化状态和维修周期。文献[2-3]使用多元统计分析方法建立轨道几何状态劣化模型。文献[4]对两次捣固之间的轨道几何劣化趋势进行线性拟合。文献[5]按照轨道特征，将荷兰铁路线路划分为不等长的轨道区段，针对每个轨道区段，分别建立轨道几何状态的线性劣化模型。文献[6]建立了高低标准差随时间的线性劣化模型。文献[7]建立了多阶段线性模型来预测轨道高低不平顺。文献[8]使用灰色理论，对轨道几何状态进行中长期预测。

随机性模型是指将轨道几何状态劣化过程视为一个随机过程，通常基于轨道几何状态历史检测数据，利用Markov过程、Gamma过程、Weibull分布等概率性方法构建轨道几何状态劣化预测模型。文献[9]使用伽马过程建立高低标准差的长期劣化模型。文献[10]同时考虑高低、轨向这两项轨道几何参数，并使用二元伽马过程建立轨道几何状态劣化模型。文献[11]采用贝叶斯方法建立轨道几何生命周期的长期劣化模型，并考虑轨道几何状态劣化的不确定性。文献[12]提出了一种分层贝叶斯方法来建立轨道几何劣化的长期预测模型。文献[13]利用马尔可夫随机过程建立轨道几何劣化模型，并评估轨道剩余寿命。文献[14-15]利用马尔可夫模型研究适用于不同轨道区段的资产管理策略。

近年来，机器学习类模型逐渐被用于预测轨道几何状态。文献[16]分别采用人工神经网络和支持向量机方法对样本数据进行训练，来预测轨道高低标准差。文献[17]利用BP神经网络对轨道几何不平顺参数进行了预测。目前机器学习类模型在轨道几何状态劣化规律建模领域的应用较少，通常需要用大量历史数据对模型进行训练和验证。

本文根据兰新线轨道几何状态劣化较快的实际情况，针对其轨道几何状态短期变化的管理需求，以确定性模型为基础，融合随机性模型的优势，考虑轨道几何状态预测的不确定性，提出了一种改进的针对200 m轨道区段的个性化的轨道几何状态劣化短期预测模型。

本文的研究结果，可以辅助铁路工务管理者准确把握轨道状态劣化趋势，科学编制捣固计划，对实现轨道安全和修理成本的双重控制具有理论意义和实际应用价值。

1 轨道几何状态劣化短期预测模型构建

1.1 问题描述

模型主要研究两次捣固维修之间，不同轨道单元区段k的轨道几何状态yk随时间x的劣化规律，其模型框架可描述为

yk=f(x,rk,εk)

(1)

式中：yk为轨道几何状态；x为劣化时间；rk为劣化率；εk为不确定性参数。

(1)研究对象

本文根据空间位置，将兰新线铁路轨道划分为K个等长的200 m轨道单元区段，将每一个200 m轨道单元区段作为研究对象，充分考虑不同空间位置轨道几何状态劣化的差异，针对每个区段进行个性化建模。由于受到多种因素的影响，每一个轨道单元区段k的劣化规律均不相同。为了使模型准确，仅利用该区段自身的历史检测数据来拟合该区段的轨道几何状态劣化规律，即式(1)中rk和εk的确定仅与轨道单元区段k的历史检测数据有关，与其他区段无关。这样，每一个轨道单元区段都有一个仅适用于自己的劣化模型，则兰新线轨道几何状态劣化规律将由K个轨道几何劣化模型构成的模型库来描述，通过Matlab编程开发，可计算得到每个区段的模型参数。

(2)轨道几何状态yk

函数的因变量yk表示轨道几何状态，本文选择轨道质量指数TQI来代表轨道几何状态yk，单位为mm。

(3)劣化时间x

函数的自变量x表示距上次捣固维修的劣化时间，单位为d。

(4)劣化率rk

参数rk表示轨道单元区段k的劣化率，用来衡量两次捣固维修之间，轨道单元区段k的劣化速率。为了充分考虑不同轨道单元区段TQI劣化的差异性，同时由于不同空间位置处的轨道单元区段之间劣化过程是相互独立的，因此本文从空间位置角度出发，针对不同的轨道区段k，利用该区段两次捣固维修之间的TQI检测数据，通过极大似然估计方法来估计该轨道单元区段的劣化率rk。

(5)不确定性参数εk

由于多种随机因素的综合作用，轨道几何状态的预测结果具有不确定性。TQI预测值的不确定性是指轨道单元区段k的TQI预测值yk与TQI的实际检测值Ik之间存在误差，由误差序列εk的概率分布来度量。通过在模型中增加随机变量εk来考虑TQI预测值的不确定性。

1.2 轨道几何状态劣化模型1.2.1 模型构建

将兰新线划分为K个轨道单元区段，对于某个轨道单元区段k，假设当前时刻为tNow，轨道单元区段k自大修以来共进行过m次捣固，捣固时刻分别为{D(1),D(2),…,D(m)}，对应m个捣固周期，分别为{Tk,1,Tk,2,…,Tk,m}，当前所处的捣固周期为Tk,m+1，下一次捣固时间为D(m+1)，Tk,m+1=D(m+1)-D(m)，见图1。根据文献[18]的结论，短期内轨道几何状态劣化通常呈现出线性特征，因此，轨道单元区段k在当前周期Tk,m+1内的轨道几何状态劣化模型为

yk=ak+rkx+εkx∈(0,D(m+1)-D(m))

(2)

式中：ak为当前周期Tk,m+1的劣化初始值，即捣固之后第一次的检测值；rk为当前周期Tk,m+1的劣化率，由上一个捣固周期Tk,m已经产生的实际检测数据所估计的劣化率来近似。参照文献[1，12，19]，假定εk服从正态分布，由上一个捣固周期Tk,m内的预测值与实际检测值之间的偏差序列进行估计，然后利用该正态分布对当前周期的预测结果进行修正。

图1 轨道单元区段k劣化趋势

1.2.2 劣化率rk的计算

(3)

则样本观测值的似然函数为

(4)

(5)

1.2.3 不确定性参数εk的计算

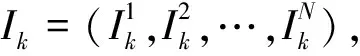
(1)利用线性劣化模型yk=ak+rkx计算轨道单元区段k不同时刻j的TQI预测值为

(6)

(2)计算轨道单元区段k不同时刻j的预测偏差序列为

(7)

(3)将偏差序列εk进行拟合，则可以得到兰新线轨道单元区段k的TQI预测偏差的正态分布，即

(8)

(9)

(10)

2 模型验证

本文以兰新线下行K600+000—K800+000里程范围内的1 000个200 m轨道单元区段为研究对象，采集了该里程范围内2015年4月至2018年8月的1 284条捣固维修数据及132次轨检车检测数据，针对每个200 m区段，利用其自身的检测数据，建立适用于该区段的轨道几何状态劣化模型，在建立Oracle数据库的基础上，使用Matlab编程开发，计算模型参数，对模型进行验证。

2.1 参数估计结果

以兰新线下行K600+000—K800+000里程范围内的每一个轨道单元区段2018年8月之前的最后一个捣固周期为研究对象，记为Q，将该捣固周期的上一个周期记为Q-1，分别对每个区段在Q周期内的劣化规律进行了建模，参数估计结果如下。

2.1.1 TQI劣化率rk估计结果

根据Q-1周期内的实际检测数据，利用公式(5)，采用Matlab辅助计算，可得到不同轨道单元区段在Q-1周期内的TQI劣化率，并以此来近似Q周期内的劣化率rk，结果见图2。

图2中横坐标为轨道单元区段编号，纵坐标为不同轨道单元区段在Q周期内的TQI劣化率rk。由图2可知，折线图波动比较明显，即不同轨道单元区段的TQI劣化率rk差异较大，这种差异是由于不同轨道单元区段所处的线路特征(坡度、曲线、桥梁、隧道、岔区等)不同，地质特征(戈壁、黄土等)不同，气候特征(风沙、严寒等)不同，施工质量不同，列车通过总重不同等多种因素造成的。这说明本文提出的以每一个200 m轨道单元区段为研究对象，分别利用每个区段自身的历史检测数据对其进行个性化建模这种方法的科学性和必要性，该方法充分考虑了影响每个轨道单元区段劣化过程的所有因素的综合作用。

以图中轨道单元区段K660+000为例，其劣化率rk为0.019 mm/d，根据现场实际资料，该区段地质类型为砂、砾、黄土状黏质砂土，容易发生沉降，其坡度为5.6‰，曲线半径为3 500 m，这些因素综合作用，导致该区段线路状态变化较快，劣化率较大，该计算结果与现场实际情况一致。

图2 兰新线下行K600+000—K800+000全部区段Q周期的TQI劣化率bk估计结果

2.1.2 TQI不确定性参数εk估计结果

同样根据轨道单元区段Q-1周期的检测数据，利用上文得到的不同轨道单元区段的TQI劣化率rk，劣化初始值ak(本文选择轨道单元区段k在某捣固周期内第一次实际检测值作为区段k在该周期的劣化初始值)，将其代入线性劣化模型中，即可得到不同区段在Q周期的TQI回归值。再根据Q周期TQI回归值与实际检测值之间的差值，计算不同区段的预测偏差序列εk。利用K-S检验方法，对1 000个区段的偏差序列εk进行正态性检验，检验结果见图3。横坐标为轨道单元编号，纵坐标为p值，红色横线代表显著性水平α=0.05。结果表明，在0.05的显著性水平下，所有区段的偏差序列均服从正态分布。由图3可知，大部分轨道区段的p值远远大于显著性水平0.05，说明这些区段的偏差序列εk高度服从正态分布。最后利用式(9)及式(10)估计不同区段TQI预测偏差序列的概率分布参数，即正态分布的标准差和均值，结果见图4。

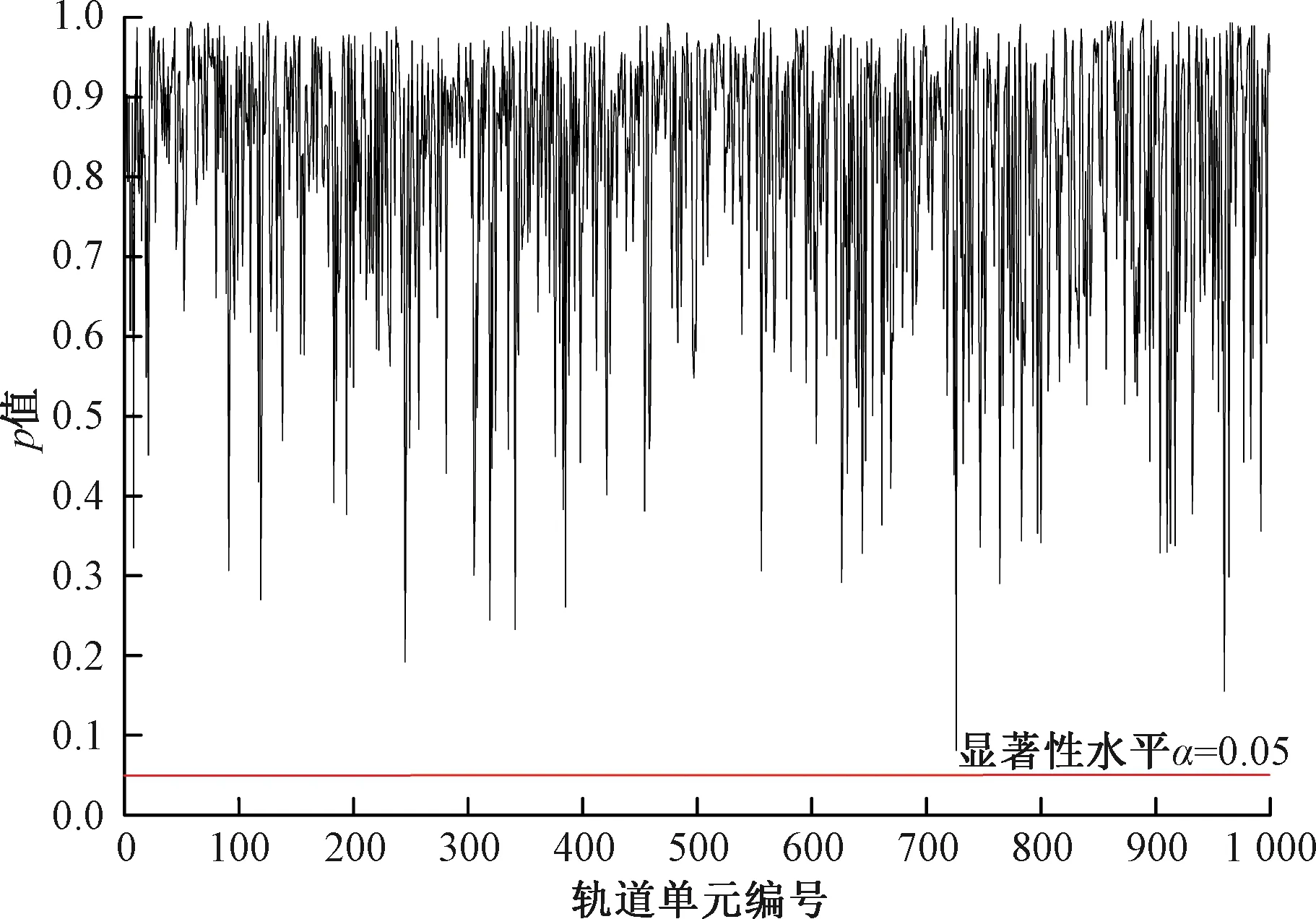
图3 兰新线下行K600+000—K800+000全部区段Q周期的TQI不确定性参数εk正态性检验结果

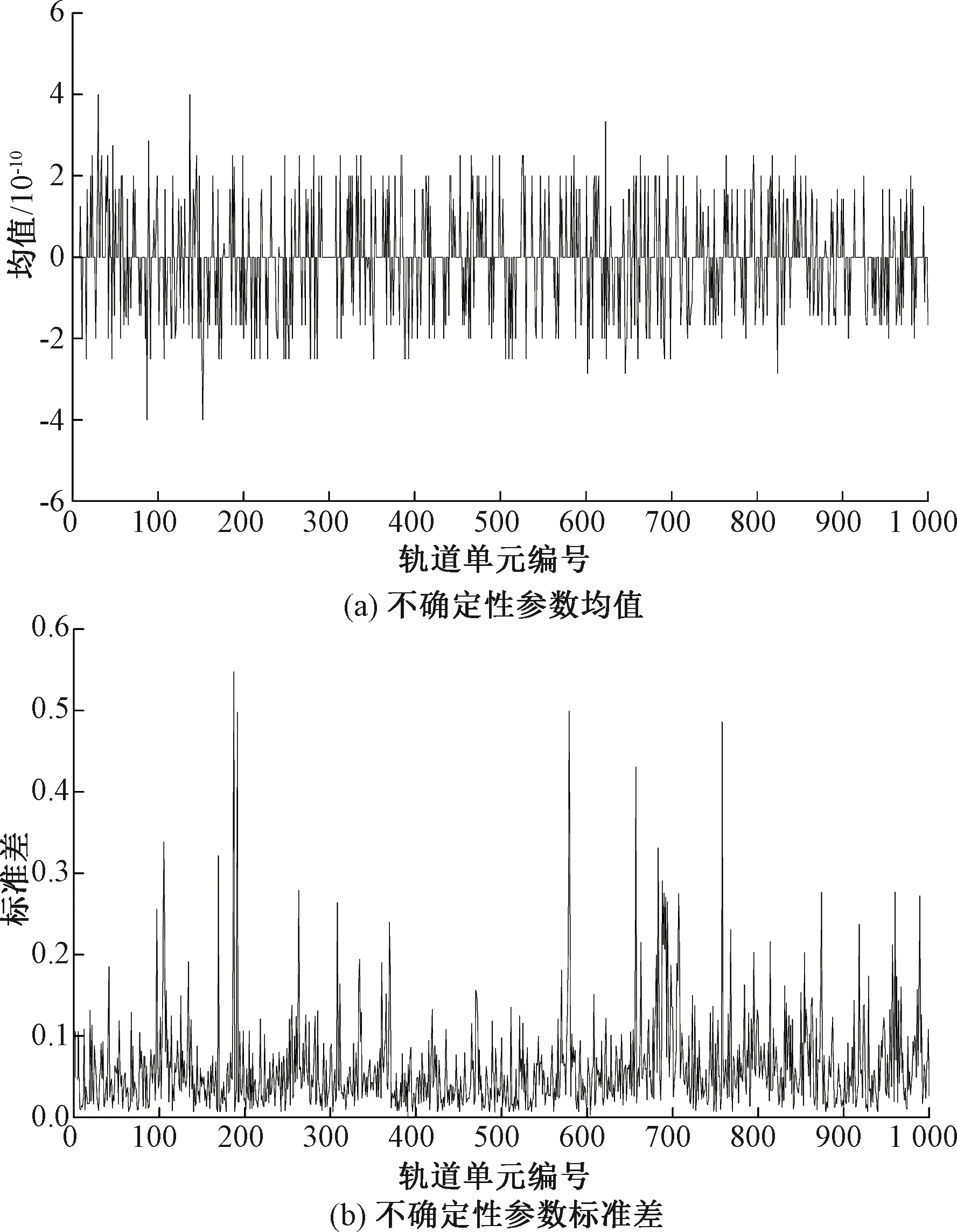
图4 兰新线下行K600+000—K800+000全部区段Q周期的TQI不确定性参数εk估计结果

由图4可知，不确定性参数εk的均值及标准差波动较明显，图4(b)中部分轨道单元区段标准差较大，说明这些区段的轨道几何状态劣化不确定性较高，若直接用线性模型进行拟合会造成较大误差。提出在线性劣化模型的基础上增加不确定性参数εk，成功减小了预测误差，提高了模型的精确性。

2.2 TQI预测结果分析2.2.1 模型拟合效果整体分析

在2.1节中模型参数估计结果的基础上，为了检验本文提出的模型对兰新线实际检测数据的拟合效果，对回归结果进行拟合优度检验。拟合优度(Goodness of Fit)是指回归直线对观测值的拟合程度，本文选择可决系数R2作为度量拟合优度的指标，R2的值越接近1，说明回归直线对观测值的拟合程度越好；反之，R2的值越小，说明回归直线对观测值的拟合程度越差[20]。兰新线下行K600+000—K800+000范围内1 000个轨道单元区段的拟合优度检验结果见图5。

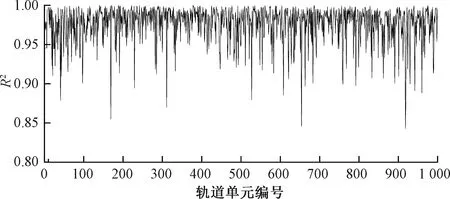
图5 兰新线下行K600+000—K800+000全部区段TQI回归直线拟合优度

对图5中兰新线下行K600+000—K800+000范围内1 000个轨道单元区段的拟合优度的分布情况进行统计分析，结果见图6。横坐标为R2范围，纵坐标为不同范围对应的比例，即处于不同R2范围内的轨道单元区段个数与样本总数的比值。结果表明，约93%的轨道单元区段的R2大于0.9，说明整体拟合效果较好。

图6 兰新线下行K600+000—K800+000全部区段TQI回归直线拟合优度统计分布图

2.2.2 典型轨道单元区段预测结果分析

为了进一步详细说明预测结果的合理性及有效性，作者选取4个典型的轨道单元区段，对模型的预测结果进行直观说明，具体见图7。

兰新线4个轨道单元区段Q周期内TQI随时间的劣化趋势见图7，横坐标为自捣固之后的劣化时间，纵坐标为不同轨道单元区段的TQI。星状点为轨道单元区段TQI的实际检测值，直线为根据实际检测值拟合出的回归直线，圆圈是对回归直线的调整，即在回归值的基础上增加了不确定性参数之后的预测值，b代表不同区段的劣化率。

由图7可知，这4个轨道单元区段的TQI劣化过程呈现出显著差异，即不同区段的初始值及劣化率均不相同，这是由于不同区段的空间位置不同，影响其劣化的因素不同，导致每个区段的劣化规律均不相同，说明了针对每个区段进行个性化建模的必要性；不同轨道单元区段的实际检测值与回归直线之间存在偏差，仅仅用线性回归进行拟合会导致预测结果不够精确。增加不确定性参数εk对预测值进行调整之后，预测结果更接近真实值，证明了本文提出的预测模型的精确性和有效性。

图7 兰新线4个轨道单元区段TQI检测值与预测值对比

3 结束语

本文以兰新线为研究对象，将线路划分为若干个等长的200 m轨道单元区段，针对兰新线轨道几何状态短期变化的管理需求，创新性地提出了一种改进的针对200 m区段的轨道几何状态劣化短期预测个性化建模方法。

模型利用每个轨道单元区段两次捣固之间自身的历史检测数据，对每个单元区段分别单独建立适用于自身的轨道几何劣化模型，实现了针对每个轨道单元区段的个性化建模；其次通过在原有确定性模型的基础上，增加不确定性参数，消除了轨道几何劣化的不确定性影响，提高了模型的预测精度。

本文提出了一种基于空间位置的模型参数标定方法。不同于既有的建模方法，本方法考虑到不同轨道单元区段之间劣化过程是相互独立的，因此仅利用每个区段自身的历史检测数据，建立了适用于该区段的轨道几何劣化模型，实现了针对每个轨道单元区段的个性化建模；其次通过在原有确定性模型的基础上，增加不确定性参数，考虑了轨道几何劣化的不确定性影响，提高了模型的预测精度。

为了验证模型的有效性，作者选取兰新线下行K600+000—K800+000里程范围内1 000个轨道单元区段作为研究对象，针对每个区段2018年8月之前最后一个捣固周期的劣化规律进行建模研究，利用Matlab编程开发，计算了每个区段的模型参数，并对这1 000个模型参数进行统计分析，结果表明约93%的轨道单元区段线性回归的可决系数大于0.9，说明模型整体拟合效果较好。在此基础上，作者选取了4个典型的轨道区段，对模型预测结果进行了进一步的直观说明，结果表明增加不确定性参数εk，消除了轨道几何劣化的不确定性影响，可以提高模型的预测精度。

本文的研究成果，可以作为今后铁路智能运维管理信息系统建设的一个模块，辅助铁路基础设施管理者准确把握轨道状态劣化规律，科学预测捣固周期，合理安排捣固维修计划和轨道状态检测计划。