基于主动电磁控制的滑动轴承-转子系统自激振动抑制数值仿真

李晓博，舒 进，牛瑞杰，姚兵印，兰 昊，陈胤嗣，李 萌，于博文

（1.西安热工研究院有限公司，陕西 西安 710054；2.西安交通大学机械工程学院，陕西 西安 710049；3.西安益通热工技术服务有限责任公司，陕西 西安 710032）

随着转子系统向着高转速、高精密性和高柔性发展，转子系统的振动控制变得越来越重要。滑动轴承由于其结构简单和承载能力强等优点被广泛用于各种转子系统。然而，高速运转时滑动轴承支承的转子系统会失稳[1-3]，失稳的主要原因是转子系统的自激振动。当转子系统转速接近其2倍一阶临界转速时，油膜半频率涡动与固有频率接近，半频率涡动与转子发生共振，如果转速继续增加这种振荡会持续不断，高速转子一旦发生自激振动将会造成非常危险的事故[4-7]。

对于旋转机械的振动抑制，不同于吸振器[8-9]和被动磁阻尼器[10]，如果采用主动电磁控制，因控制力是电流通过线圈产生电磁力施加在转子上，控制装置与转子无接触无摩擦，不会造成机械磨损。另外，由于其具有可控性和高可靠性，通过调节控制器参数可以为转子系统提供不同的额外的刚度和阻尼[11-12]，非常适用于高速转子系统的振动抑制。

为了探究主动电磁控制的抑振效果，本文建立了滑动轴承支承的转子系统动力学模型，依据转子模型的参数设计了主动电磁控制装置和控制器，并且通过数值仿真分析了转子系统在主动电磁控制下的振动特性。

1 轴承-转子系统动力学模型

1.1 转子模型

基于有限元法建立单圆盘转子动力学模型[13]，图1为单圆盘转子模型，其仿真参数见表1。图1中转子划分为11个节点，采用Timoshenko梁单元建立转子系统有限元模型。忽略转子内阻尼和剪切变形的影响，圆盘简化为集中质量叠加在相应的节点上，圆盘上的偏心质量在转子旋转时产生不平衡力。忽略转子轴向的运动，只考虑横向弯曲振动，因此每个节点仅包含2个线位移和2个角位移，整个转子系统包含44个自由度。转子的运动方程可以表示为

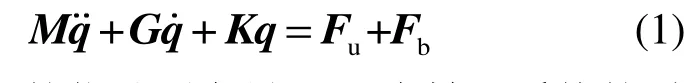
式中：q为转子的位移列向量；M为转子系统的质量矩阵，G为转子系统的转动惯量矩阵；K为转子系统的刚度矩阵；Fu为偏心质量产生的不平衡力列向量；Fb为轴承油膜力列向量。

图1 单圆盘转子模型Fig.1 The single-disk rotor model

表1 单圆盘转子仿真参数Tab.1 Simulation parameters of the single-disk rotor

1.2 油膜力模型

非线性油膜力模型采用短轴承油膜力模型[14]。对圆柱滑动轴承进行仿真，其结构参数见表2。

表2 滑动轴承仿真参数Tab.2 Simulation parameters of the oil-film bearing

非线性油膜力的计算是基于短轴承理论，假设润滑油黏度不变且不可压缩，则轴承内的油膜压力分布的Reynolds方程无量纲形式[14]可表示为

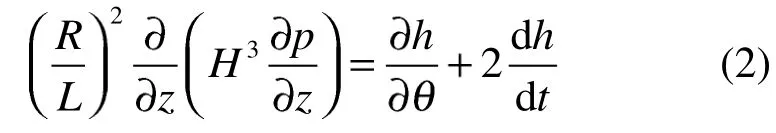
式中：p=P/P0为无量纲油膜压力，相对单位为P0=6ωμR2/C2；P为油膜压力，Pa；ω为轴的转速，rad/s；μ为润滑油黏度，Pa·s；R为轴承半径，m；C为轴承间隙，m；z=2z/L为无量纲轴向坐标，其相对单位为L/2；L为轴承长度，m；θ=x/R为无量纲x方向坐标，其相对单位为R；H=h/C为油膜厚度的无量纲表示，其相对单位为C；h=C-xpcos(φ)-ysin()为油膜厚度，m；x和y为轴颈在轴承中的位置；为轴颈的偏位角，rad；t为时间，s。

通过式（2）可以得到施加在转子上的油膜力，当已知轴承间隙C、润滑油黏度和转速后，轴承施加在转子x和y方向的油膜力可以表示为：

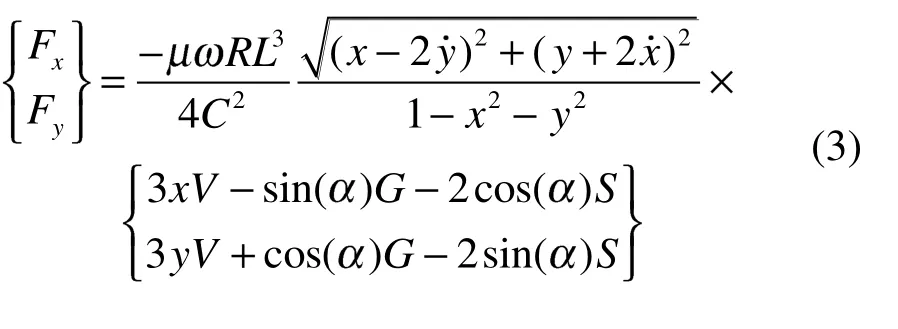
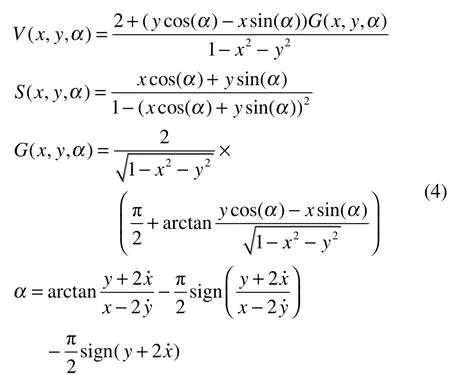
式中：Fx和Fy为x和y方向的轴承力，N；和为对轴颈在x和y方向的位移求导，m/s。

2 主动电磁控制系统模型

主动电磁控制系统是一种机电一体化装置，涉及机械动力学、控制理论以及测试技术等，它利用线圈产生的电磁力将转子稳定悬浮在参考位置处，使转子和主动控制装置间没有机械接触，为了实现主动电磁控制系统对转子的平稳控制，需要采用闭环控制策略并设计控制器[15-16]，根据转子的悬浮状态不断地改变电磁力的大小和方向。

2.1 主动电磁控制系统设计

对转子x和y方向分别进行独立控制，以其中一个方向为例，单自由度主动电磁控制系统的结构如图2所示。

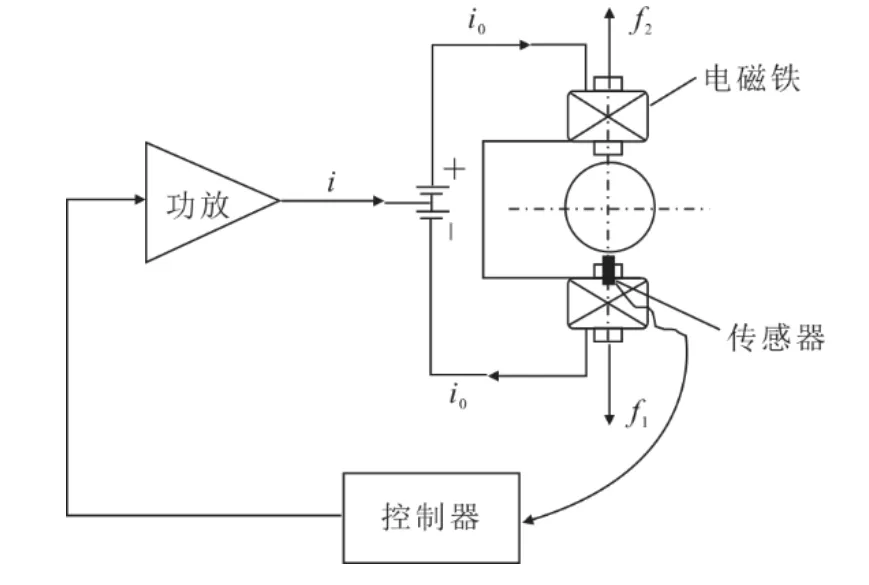
图2 单自由度主动电磁控制系统Fig.2 The one DOF active electromagnetic control system

图2中主动电磁控制系统包含转子、1对电磁铁、位移传感器、控制器以及功率放大器5个部分。主动电磁控制系统采用电流驱动方式[17]，单自由度方向的一对电磁线圈采用差动驱动。如果将2个电磁铁的中心设置为目标位置，则转子先由偏置电流i0通过线圈产生的电磁力吸到任意一方，位移传感器实时监测转子的位移，并将此时转子的位移信号传送到控制器，控制器根据控制算法基于转子实际位置与目标位置的误差计算电流控制信号，控制信号则通过功率放大器转化为控制电流i，电流通过电磁线圈产生相应的电磁场，这样转子在电磁场中受到2个电磁铁控制力f1和f2的作用而稳定悬浮在目标位置。

根据转子结构参数可知，转子质量约为2.8 kg，因此偏置电流产生的力应该大于等于转子质量。假设所用磁材料是各向同性的，磁路中的磁场是均匀分布，忽略磁路的漏磁以及涡流效应等非理想因素，结合所需要的悬浮力以及转子直径设计，主动电磁控制系统仿真参数见表3。

表3 主动电磁控制系统仿真参数Tab.3 Simulation parameters of the active electromagnetic control system

基于表1设计参数，图2中的单自由度主动电磁控制系统的运动方程可以表示为

电磁铁产生的控制电磁力为

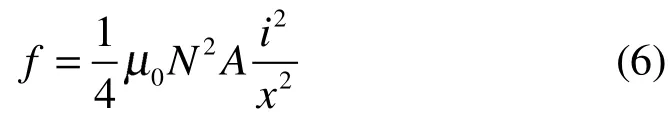
式中：fi为电磁铁产生的电磁力，N；m为转子质量，kg；μ0为真空磁导率，(π×10-7)H/m；N为线圈匝数；A为磁极面积，m2；i为控制电流，A；x为转子的位移，m。

由于主动电磁控制系统采用差动驱动方式，则在差动驱动下，一个线圈的电流为偏置电流和控制电流两部分电流之和，另一个线圈的电流为两部分电流之差。因此线圈产生的合力为

式中：i0为偏置电流，A；x0为电磁铁与转子之间的距离，m。

将式(7)在平衡位置（i=0，x=0）处进行泰勒展开，并略去高阶项，得到电磁力的线性表达式

式中，ks为位移刚度，ki为电流刚度。

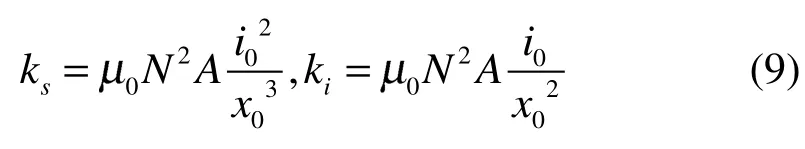
因此，根据系统的运动方程可以得到转子在电流控制下的传递函数为

2.2 主动电磁控制系统仿真

主动电磁控制系统是开环不稳定系统，因此需要设计闭环反馈控制器。本文采用PID控制算法，该算法是通过给定值和输入值的偏差结合控制算法生成控制信号，从而控制被控对象。控制器的参数则是通过极点配置法[18]确定，主动电磁控制系统如图3所示，PID控制器参数见表4。

图3 主动电磁控制系统Fig.3 Block diagram of active electromagnetic control system

表4 PID控制器参数Tab.4 The active electromagnetic control system’s parameters

采用MATLAB/Simulink进行仿真，仿真模型中转子的初始位移设置为0.6 mm，参考位置信号为0，仿真时长为0.5 s。图4为转子从初始位置悬浮至参考位置的结果。

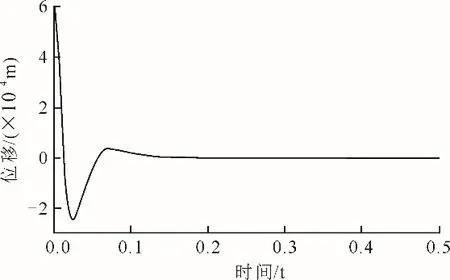
图4 转子悬浮响应Fig.4 Suspension response of the rotor

由图4可见，主动电磁控制系统在大约0.2 s后稳定，初期产生了一定的超调，超调量最大为0.25 mm，远小于电磁铁和转子之间的气隙0.6 mm，不会造成转子磨碰现象。图5为转子稳定悬浮0.25 s时给转子施加5 N外力的结果。由图5可见，转子稳定悬浮后，施加外力转子会偏移平衡位置但在控制器的作用下很快又回到平衡位置，即设计的PID控制器可以实现转子的稳定悬浮。

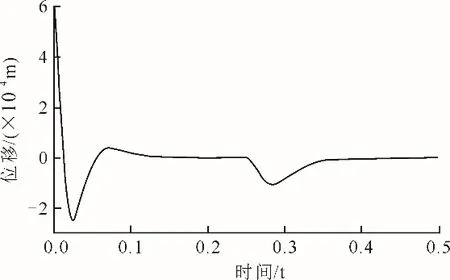
图5 转子受外力时的响应Fig.5 Response of the rotor to external forces

3 主动电磁控制下转子振动分析

为了清楚展示主动电磁控制对自激振的抑制效果，分别计算滑动轴承支承转子在未采用主动电磁控制和采用主动电磁控制时轴承处的不平衡振动响应。图6为转子系统受力分析，圆盘偏心质量产生的不平衡力叠加在节点6上，2个轴承的非线性油膜力分别施加在节点3和节点9上，主动电磁控制系统的刚度和阻尼施加在节点5所在的刚度和阻尼矩阵中，控制器参数选取表4中的参数，用四阶龙格-库塔法求解该动力学方程。

图6 转子系统受力分析Fig.6 Force analysis of the rotor system

对未采用主动电磁控制时的转子在转速范围为8~120 Hz时进行升速仿真。由于转子是对称结构，且不平衡力施加在转子对称中心，因此两轴承处的响应一致。图7为轴承1处x和y方向的位移响应。从图7可以看出，转子的振幅随着转速的上升而增加，转速超过48 Hz后逐渐减小，当转速上升到92 Hz后再次增大且保持不变。

图7 未采用主动电磁控制升速过程中轴承1处位移响应Fig.7 Displacement response of bearing 1 during run-up

为了更加直观地得到其振幅、转速与涡动频率的关系，图8给出了轴承1处x方向响应的瀑布图。图8中的结果与图7中x方向的位移响应相对应，随着转速的增加，同步振动的振幅逐渐增大，在48 Hz时出现第1个峰值，此时为转子的一阶共振频率。转子跨过共振频率后振幅逐渐减小，在接近2倍的一阶共振频率时半频率涡动起主导作用，图8中转速高于92 Hz的部分由于自激振动导致振幅显著增加。

图8 未采用主动电磁控制轴承1处x方向位移响应瀑布图Fig.8 Waterfall diagram of displacement response in x direction at bearing 1 location

图9为采用主动电磁控制后支承转子的轴承在转速范围8~120 Hz时升速的位移响应结果。从图6中可知，由于主动电磁控制系统的刚度阻尼施加在节点5处，并不在转子对称中心，因此2个轴承处的振动响应不同。从图9可以看出，在转速范围内2个轴承的振动响应趋势相同，随着转速的增加，同步振动的振幅增大，在70 Hz出现第1个共振峰，且转子跨过共振频率后振幅逐渐减小，且轴承1的振动幅值明显小于轴承2，这是由于施加的电磁主动控制系统更加靠近轴承1。图10和图11分别为轴承1和轴承2处x方向位移响应的瀑布图。

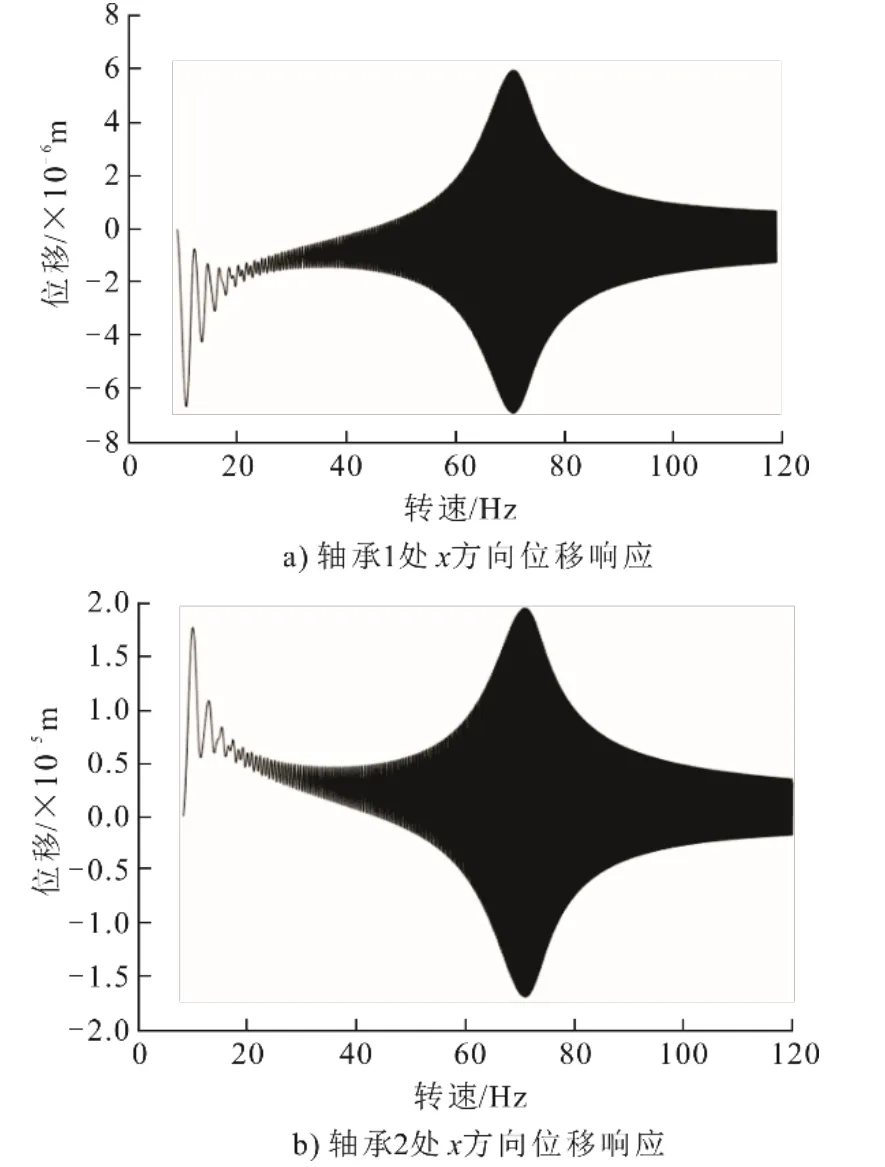
图9 采用主动电磁控制后转子轴承处响应Fig.9 Response of bearings under active electromagnetic control

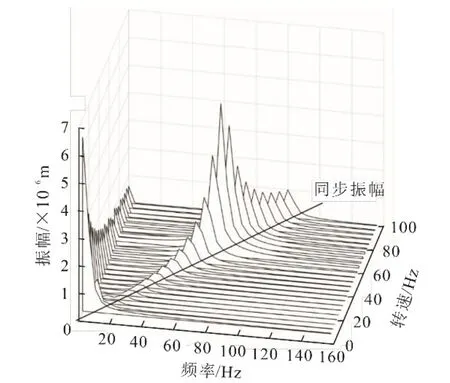
图10 采用主动电磁控制后轴承1处x方向位移响应瀑布图Fig.10 Waterfall diagram of displacement response in x direction at bearing 1 location

图11 采用主动电磁控制后轴承2处x方向位移响应瀑布图Fig.11 Waterfall diagram of displacement response in x direction at bearing 2 location

通过对比图8与图10和图11可以看出，当采用主动电磁控制后，转子系统的一阶固有频率从48 Hz提高到70 Hz，且2个轴承的振幅较未施加主动电磁控制均有所减小，并且在转速范围8 ~120 Hz内未出现自激振动。

以上仿真结果表明，采用主动电磁控制能够有效抑制自激振动。CHEN等人[19]进行了电磁激励器抑制转子系统油膜振荡的试验研究，其主动电磁控制采用PD闭环反馈控制。在未控制时发生了自激振动，而当自激振动将要产生时进行主动电磁控制自激振动即被消除。本文自激振动抑制仿真结果与文献[19]实验结果一致，证明了本文主动电磁控制下的非线性油膜力滑动轴承柔性转子系统动力学模型仿真结果的正确性，该模型可以为滑动轴承在高速工况下的振动抑制以及主动电磁控制系统的应用提供理论依据。

4 结 论

1）通过建立非线性油膜力滑动轴承柔性转子系统动力学模型，得到轴承处转子在未采用主动电磁控制时的响应，通过瀑布图分析得到其固有频率和自激振发生的频率。依据转子模型的参数设计了主动电磁控制装置和控制器，并且通过数值仿真分析了转子系统在主动电磁控制下的振动特性。

2）未采用主动电磁控制时，自激振动发生在约2倍的一阶临界转速附近；控制器参数影响着主动电磁控制系统的刚度和阻尼，采用PID控制器时，系统的刚度与参数P有关，系统的阻尼除了与I和D有关外，还与被控对象的频率有关。

3）采用主动电磁控制时，由于主动为被控对象提供了额外的刚度和阻尼，不但可以提高发生一阶共振时的频率，降低过临界时振动幅值，还可以有效抑制自激振动的发生。因此，对于高速旋转的转子系统，采用主动电磁控制系统，通过设计合理的控制器，可抑制自激振动提高转子系统的稳定性。