基于YIN算法的乐器单旋律音高的提取

张 岩, 王 伟

(沈阳师范大学 计算机与数学基础教学部, 沈阳 110034)

旋律通常指若干乐音经过艺术构思而形成的有组织、节奏的序列,其特征是按一定的音高、时值和音量构成,并由具有逻辑因素的单声部进行。旋律的3个主要特征中,音高是最重要的。国际音乐信息检索测评(Music Information Retrieval Evaluation Exchage,MIREX)将旋律定义为对应显著性人声或乐器中感知音高的基频值序列[1]。在旋律进行中,由于音高走向的变化而形成的起伏线条,叫旋律线。音乐学中,按照音乐作品旋律线的数量,将音乐分为单声部音乐和多声部音乐。单声部音乐指同一时刻只有一个音符发音,如独唱、管乐器的独奏、演奏单旋律的弦乐器独奏等。多声部音乐是指有2个或者更多的音符同时发声的音乐,这些音符可以来源于不同的声源,如歌声、吉它或贝斯等,也可以来源于能同时发2个以上音的声源,如钢琴[2]。

单旋律提取是以单声部音乐为对象,对旋律的音高和时值等主要特征进行提取。从音乐信号中提取主旋律的方法主要分为3类:基于显著性的方法、基于源分离的方法和基于机器学习的方法[3]。单旋律的提取侧重所提取旋律的准确性、高效性和可视性。从音乐复杂性和计算复杂性分析,为了实现旋律快速和实时的轮廓化,基于显著性的方法比较适用。单旋律提取可以应用于乐曲创作、音准分析、调式分析等,因此具有重要的研究和应用价值。

1 音高显著性和音高检测

1.1 音高与基频

音高是由发音体发出的基本频率决定的,基频通常用F0表示。音高越高对应的f0越大。当发音体由于震荡而发出音时,每个音不仅仅包括基频正弦波的基音,还同时包括许多频率较高的正弦波的泛音[4],其中频率最低的正弦波即为基音,而其他频率较高的正弦波则为泛音。基音是区别音高的主要元素,泛音决定音色。复合波的振幅是由基音的振幅和各组泛音的振幅重叠而成,若振幅方向相同则相加;若振幅方向相反则须要相减。复合波也是一种周期性的振动波[5]。音分为谐和音与不谐和音。谐和音指谐波(或谐波分量)的频率是基频的整数倍,当然有许多乐器(如弹拨弦乐器)产生的音并不是完全谐和的。不谐和音和不完全谐和音都是乐音,音乐中的旋律等均由乐音构成[6]。

1.2 音高检测(基频估计)

音高检测通常包括时域分析、频域分析和时频域分析。在时间域内对信号进行滤波、放大、统计特征计算、相关性分析等处理,统称为信号的时域分析。频域分析采用傅立叶变换将时域信号变换为频域信号,从频域角度来了解信号的特征。时频域分析是将时域与频域的处理方式结合起来,它将信号分割成时间帧,进行时频变换,分析信号在时间域内的频谱的特征。针对单旋律提取的简单性,采取不用进行时频转换的时域分析来进行音高检测,以降低计算复杂度,提高实时应用性。时域分析算法主要包括自相函数(Auto Correlation Function,ACF)算法和YIN算法。

2 YIN算法

2.1 自相关函数算法

YIN算法以自相关函数算法为基础。对于乐曲数字化的有限离散信号,若其长度为N,它的自相关函数Rx(k)定义为

(1)

其中k是时移参数,显然当k=0时得到最大的R值,也就是信号与信号本身相似度最大[7]。自相关函数在基音周期的整数倍处取得最大值,计算2个相邻的最大峰值间的距离,就可以估计出基音的周期,从而得到基音的频率。

乐音信号复合波的大多数峰值并不能反映基频的周期,而只有少数的峰值与基频有关。为了强化反映基频周期的峰值,减少谐波成分峰值的干扰,降低自相关算法的计算量,需要对音频信号进行中心削波处理。通常采用的三电平中心削波函数是

(2)

式(2)中,x(n)是原始乐音信号,Cl是削波电平,y(n)是削波后的乐音信号[8]。一般地,削波电平是由乐音信号的峰值的固定百分比来确定的,可以取峰值幅度的60%～70%。

2.2 YIN算法

YIN算法可以一定程度地解决确定哪个峰值对应的是基频的峰值的问题。YIN函数的定义Dx(k)为[9]

(3)

公式(3)中,以信号差平方和函数代替了公式(1)中的信号积和函数。这样,在信号周期整数倍数处,YIN函数值为幅度差平方和,并且取值均为零。很显然,查找零值的时间效率要高于求最大值的时间效率。

利用YIN算法时,考虑基频提取的实时性,通过实验测试三电平中心削波对YIN算法效率的影响。具体测试了不同采样点数量规模的情况下,只进行YIN算法的运行时间,以及先进行三电平中心削波后进行YIN计算的运行时间,测试数据如表1所示,采样点数为512时的YIN函数波形如图1所示。实验结果表明,随着处理的采样点数的增加,三电平中心削波会一定程度地增加YIN算法的运行时间;三电平中心削波减弱了YIN算法在信号周期处获得零值或者近零值的显著性,增加了获取周期位置的复杂性。因此, YIN算法不必进行自相关函数算法中的三电平中心削波处理。

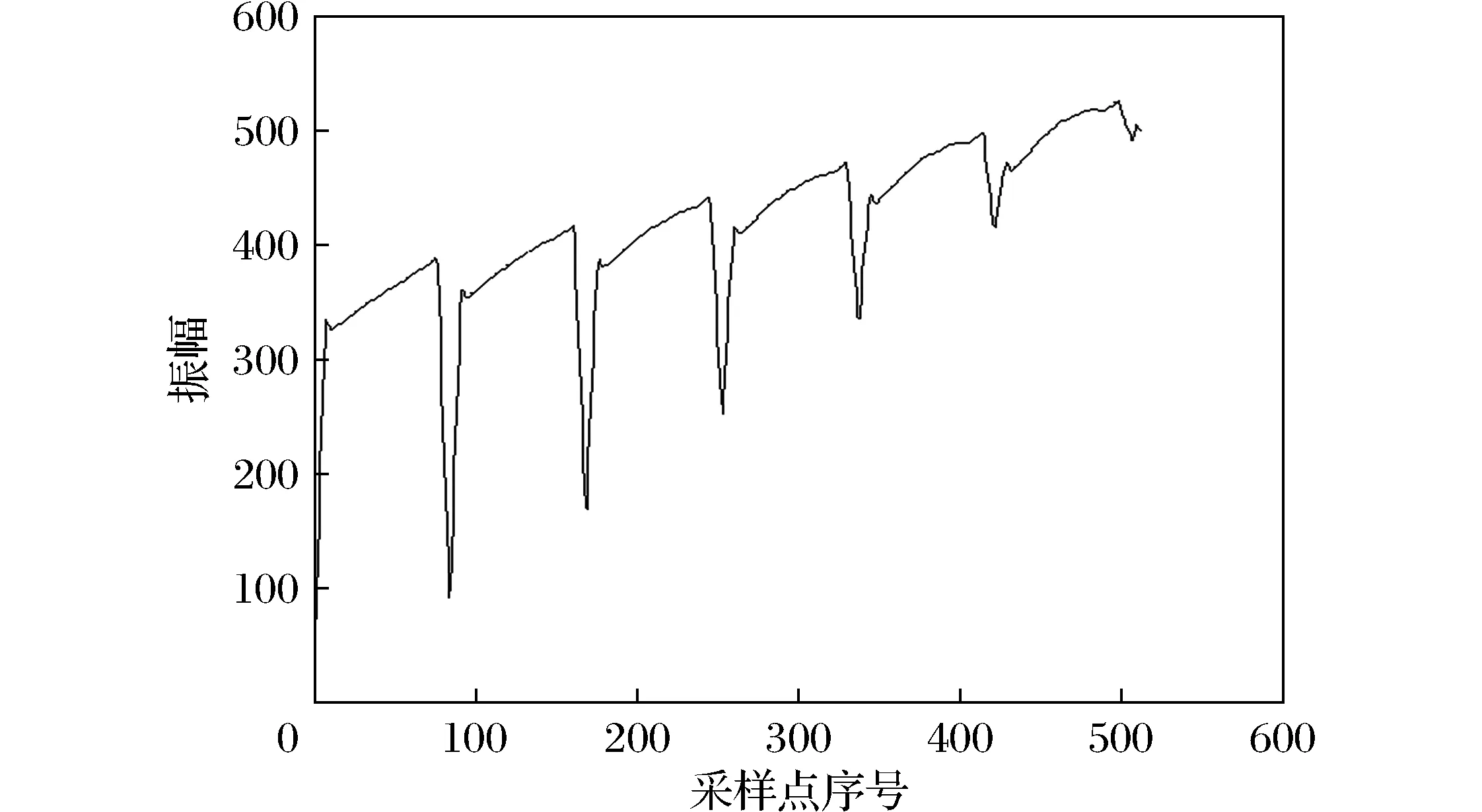
图1 乐音信号某512采样点三电平中心削波后YIN波形

表1 YIN算法与三电平中心削波+YIN算法的运行时间对比(单位: 秒)

3 单旋律乐曲的音高提取算法的实现

3.1 利用YIN算法对乐音信号的分析帧长的估算

以小提琴为例,从低到高的4根琴弦分别为E、A、D、G,标准的空弦音从低到高是g=196 Hz、d1=294 Hz、a1=440 Hz、e2=659 Hz,每把小提琴的实际频率分布是不同的[10]。假设取最低频率确定的分析帧长,当分析帧帧长取128(1 024个采样点的时间约为24 ms,128个采样点的时间约为3 ms)时,不能包含最低频率的2个周期,经过YIN算法实验证明,波形中包含1个最低点,但是不能判断该采样点即是周期点,所以需要扩展分析帧长点数;当扩展帧长点数为512时,采样时间约为12 ms,包含最低频率的2个周期,波形出现了周期性的波动,如图2所示。以上实验表明,512个点作为分析帧的帧长是适当的,依此也可以将分析帧的一半,即256个点作为帧移。

图2 乐音信号某512个采样点的YIN波形

3.2 获取乐音信号分析帧中近零点的方法

从图中的YIN函数波形来看,对于YIN算法理论上的零点存在2个实际的问题:

1)理论上应该在信号周期处获得零点,但是由于采样时未必能取到信号周期所在处的点,所以只能从YIN函数值中获得近零点。

2)当时移k非常小的时候,Dx(k)的值也非常小,也往往小于周期处近零点的值。当k=0时,往往就是Dx(k)的零点或者是最接近零的近零点,影响获取正确的近零点。为了取消时移k非常小的影响,可以采用累积平均归一化差分函数,其公式为[11]

(4)

利用累积平均归一化函数,对于图2中的采样帧进行处理,处理结果如图3所示。显然,经过处理后,消除了时移非常小时的YIN函数值对提取近零点的影响。

图3 乐音信号某512个采样点的YIN累积平均归一化波形

3.3 YIN算法提取音高的实现

在Matlab环境中,读入小提琴无伴奏的WAV乐曲文件,利用YIN算法提取该分析帧的基频的周期,即采样点序号。若经算法计算得出基音周期为T(i),则相应的基音频率为F(i)=fs/T(i),其中fs表示乐曲采样频率[12]。Matlab代码如下[13]:

[x1,fs,nbit]=audioread(′xtq.wav′); %fs为采样频率44.1kHz,nbit为采样位数16,x1为读取的归一化后幅

%值[-1,1]之间的乐音信号,共有采样点数*2个数据, 2表示双声道

[Row,Col]=size(x1); %采样点数组的行数和列数

N=512; %确定分析帧的帧长点数

Ind=[];AM=[];Pitch=[];

for FM=1:200 %选取前200个分析帧

N1=256*(FM-1)+1; %某分析帧的起始采样点序号,帧移是256

N2=N1+1024-1; %某分析帧的终止采样点序号

x2=x1(N1:N2,:);

D=[];Dn=[]; %以下3行是累积平均归一化的初始化

Dn(1)=1;sumn=0;

for k=2:N %延迟N个点数

sum=0;

for j=1:N %YIN函数计算

sum=sum+(x2(j)-x2(j+k))*(x2(j)-x2(j+k));

end

D(k)=sum;

sumn=sumn+D(k); %以下2行是累积平均归一化

Dn(k)=D(k)/(sumn/k);

end

[A,Pos]=min(Dn); %求第一个近零点

AM(FM)=A;

Ind(FM)=Pos; %求近零点的采样点序号

Pitch(FM)=44100/Ind(FM); %求基频

end

4 结 语

根据十二平均律,计量上将一个八度音程即2倍频率之间分成12个音级,每2个相邻音级相差100音分(cent)。2个相邻音级的频率比是2(1/12)(约1.059 463)。2个相邻音分的频率比是2(1/1 200)(约1.000 577 79)[14]。音列中乐音i 的标准频率公式为F(i)=fa1*2(n/12),其中fa1= 440为第一国际高度,n 为乐音i到a1间隔的半音数目,当乐音i比音a1低时,n取负数[15]。以前面的200个分析帧(帧长512点,帧移256点)提取的音高序列为例,提取的频率和标准频率之间存在偏差,表现为音级和音级之间不是准确的2(n/12)的关系,进一步通过消除偏离频率严重的野点来修正提取的频率。以fa1=440 Hz为基准,可以通过若干次的1.059 463的倍数来计算标准音级的频率。对于某个音级,可以通过若干次的1.000 577 79的倍数来计算音级的各个音分的频率。如果是音准检测,那么10个音分以内的偏差下,可以认定音级;如果是提取旋律,那么50个音分以内的偏差下,可以认定音级,或者结合提取频率对应的帧数来进一步判断,当帧数少于2帧时,可以认定为野点,否则可以进行频率修正,如表2所示。显然,经过修正后,可以提高乐音频率提取的准确度。

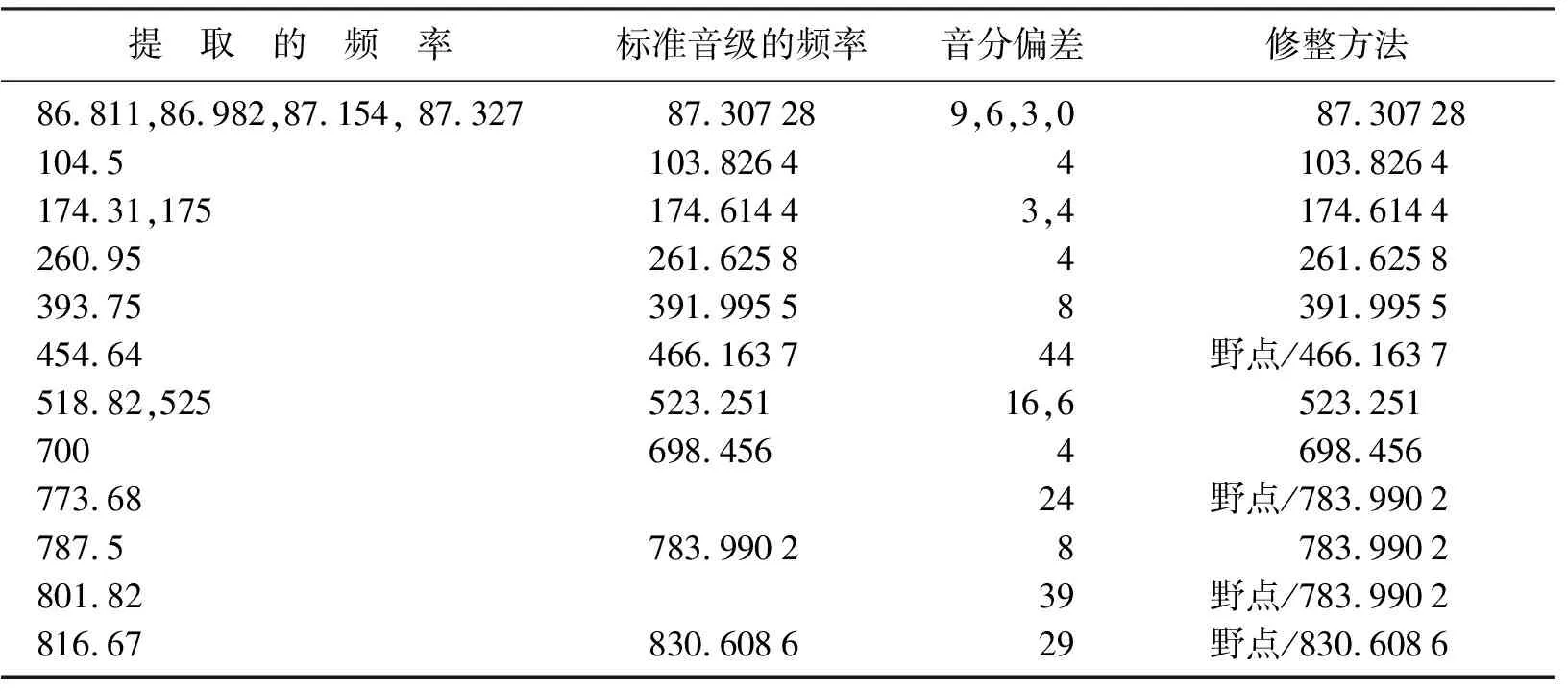
表2 提取频率的修正方法