天然气紧急截断阀控制器优化

张 敏，王德国,2

(1.中国石油大学(北京)机械与储运工程学院，北京 102249； 2.油气资源与工程国家重点实验室，北京 102249)

引言

天然气管道在长期使用过程中，有可能存在泄漏，必须紧急切断气源，以免发生事故。因此天然气紧急截断阀的研究具有重要意义[1]。目前对于天然气紧急截断阀的研究，主要偏重于管道压力预测[2]以及紧急截断阀阈值压力的分析[3]，对于紧急截断阀本身的特性研究较少。天然气紧急截断阀在使用过程中，由于开启瞬间控制气缸内部压力突变，造成截断阀阀门开启突变，从而引起截断阀内部振动、冲击，产生噪声，并使得内部零件损坏。现有的气动截断阀研究中，徐文涛等[4]对截断阀内部结构进行优化，以减小截断阀内部气体压力突变。赵明等[5]根据使用经验对截断阀的零件材料进行优化和强度校核。SURESH[6]对截断阀的尺寸和重量进行优化。鲍军等[7]采用TRIZ理论对截断阀的密封性进行优化。杨豪杰[8]对截断阀的模态进行优化。

通过调研天然气管线紧急截断阀使用过程中的工况，设计了一种天然气紧急截断阀控制器[9]，通过该控制器控制紧急截断阀的开启和关闭。为了解决天然气紧急截断阀出现的问题，对紧急截断阀控制器的参数进行优化，使得进入截断阀控制气缸的气体压力平稳过渡。因此可以进一步改善天然气紧急截断阀的使用工况，减小截断阀的振动及噪声，提高其使用寿命。

1 紧急截断阀控制器数学模型及性能分析

天然气紧急截断阀控制器外形如图1所示，工作原理如图2所示。图2中，该控制器包括3部分：主阀、二位四通阀和手动复位阀。在正常情况下，天然气管道内的高压气体从主阀的1口进入主阀芯I腔，对阀芯产生向左推力。在主阀芯左端安装压缩弹簧。当气体产生的作用力大于弹簧的弹力时，主阀芯左移。主阀芯与二位四通阀阀芯相连接，因此带动二位四通阀阀芯左移，二位四通阀处于右位。常态下手动复位阀处于右位。因此，天然气管道减压阀输出的低压气体，通过手动复位阀的4口和5口，并通过二位四通阀的6口和3口进入紧急截断阀控制气缸，气缸低压腔气体通过二位四通阀2口和7口排出。此时，控制气缸活塞打开天然气紧急截断阀，天然气管道内的气体通过截断阀。当天然气管道存在泄漏时，管道内压力下降，对控制器主阀芯的作用力小于弹簧推力，主阀芯右移，二位四通阀阀芯处于左位，切断紧急截断阀控制气缸内的气体，天然气紧急截断阀关闭，天然气主管道内气体被切断。由于二位四通阀在紧急截断过程中，将手动复位阀芯推向左位，因此，当天然气管道泄漏事故处理完成后，人为压下外部复位按钮，手动复位，使得4，5口接通，为下次二位四通阀阀芯开启做好准备。

图1 天然气管道紧急截断阀控制器

图2 天然气管道紧急截断阀控制器原理图

1.1 主阀芯数学模型

主阀芯在运动过程中，受到惯性力、黏性阻尼、摩擦力、弹簧反作用力、重力等的作用。由于重力与主阀芯水平移动方向垂直，因此忽略不计。气体对阀芯产生向左的推力，弹簧对阀芯产生向右的推力。根据受力情况，建立主阀芯的二阶微分方程：

(1)

F=pA

(2)

(3)

式中，M为主阀芯的质量，kg；B为阻尼系数，N·s/m；Kv为弹簧刚度，N/m；x为主阀芯位移，m；x1为弹簧预压缩量，m；F为主阀芯受到的气体作用力，N；p为气体压力，Pa；A为主阀芯有效面积；D为主阀芯外径，m；d为主阀芯活塞杆直径，m。

主阀芯位移x是时间t的函数，以气体压力p为输入量，位移x(t)为输出量，对式(1)～式(3)进行拉普拉斯变换，可得传递函数：

在MATLAB下建立其Simulink仿真模型，如图3所示。对模型进行仿真，根据所研制的控制器实体，选取参数：B=700 N·S/m，Kv=100000 N/m，Kvx1=900 N，M=3.7 kg，D=40 mm，d=22 mm。仿真结果如图4所示。

从图4可以看出，气体压力作用在主阀芯瞬间，阀芯存在短时间的振荡过程，最终趋于稳定。由于主阀芯移动存在振荡，导致二位四通阀阀芯位移振荡，最终影响到截断阀控制气缸内气体压力振荡，造成截断阀开启瞬间的波动，使得截断阀产生振动及噪声。因此，对二位四通阀与截断阀控制气缸组成的系统进行分析，根据分析结果，通过减小控制气缸活塞移动量波动，降低截断阀的振动与噪声。

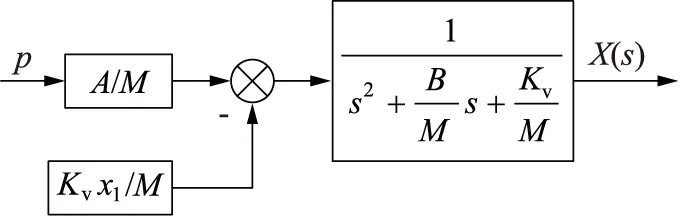
图3 主阀芯位移传递函数方框图

图4 主阀芯位移

1.2 二位四通阀芯开口处气体流动数学模型

气体从二位四通阀阀芯开口处流入，假设按照理想气体流动模型[10-11]，且气体变化过程为绝热过程，则通过二位四通阀阀芯开口的流量为：

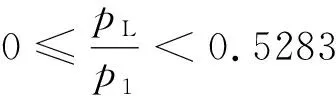
(6)

式中，qm为质量流量，kg/m3；p1为阀芯入口处压力(上游压力)，Pa；pL为阀芯出口处压力(至截断阀控制气缸内，下游压力)，Pa；Cd为阀口的流量系数，取0.68； R为气体常数，取287.1 J/(N·K)；k为气体绝热常数，取1.4；A1为阀芯节流口有效面积，m2。

1.3 截断阀控制气缸数学模型

根据气缸内气体的连续性方程[12-13]，可得：

(7)

式中，T10为缸内的初始温度，K；p10为缸内的初始气体压力，Pa；AL为活塞有效作用面积，m2；y为控制气缸活塞的位移，m；V10为控制气缸进气腔的初始气体体积，m3。

控制气缸为单作用缸，活塞一端受到气体作用力，另一端受到弹簧推力。当控制气缸通入高压气体时，活塞将弹簧压缩，截断阀开启。当控制气缸未通入高压气体时，弹簧弹力将活塞复位，截断阀关闭。因此，控制气缸活塞的受力方程为[14]：

(8)

式中，ML为活塞及活塞杆质量，kg；BL为活塞与缸筒阻尼系数，N·s/m；kL为弹簧刚度，N/m；FL为其他外力，N。

根据式(1)～式(3)和式(5)～式(8)，即可得到控制气缸活塞的位移及其进气腔内压力变化。活塞的位移变化曲线如图5所示，可以看出，在开启瞬间，活塞位移出现振荡。因此，为了使控制气缸活塞瞬态特性平稳，需要对控制器进行优化设计。

图5 截断阀气缸活塞位移

1.4 控制器主阀参数对截断阀控制气缸活塞位移的影响

1) 阻尼的影响

改变控制器主阀芯与阀体的阻尼，观察控制气缸活塞的位移变化，如图6所示。需要注意的是，控制气缸活塞位移为30 mm，为了反映活塞位移的瞬态特性，采用阶跃信号对其进行观察，因此纵坐标为1，无量纲。从图6可以看出，当阻尼为300 N·s/m时，超调量23%；当阻尼为700 N·s/m时，超调量为17%。因此，随着阻尼的增加，超调量减小，振荡过程减缓，但其峰值时间不变。

图6 阻尼变化对气缸位移的影响

2) 主阀芯质量的影响

改变主阀芯质量，观察控制气缸位移的阶跃响应，如图7所示。当阀芯质量为2.7 kg时，超调量为20%，调节时间为0.05 s，当阀芯质量为4.7 kg时，超调量为16%，调节时间为0.07 s。因此随着质量的增加，超调量下降，响应时间变慢。

图7 主阀芯质量对气缸位移的影响

3) 弹簧刚度的影响

改变主阀芯弹簧刚度，观察控制气缸位移的阶跃响应，如图8所示。当弹簧刚度从1×105N/m增加到2×105N/m时，超调量(相对于各自稳态值)从5%增加到17%，调节时间均为0.05 s。需要注意的是，当弹簧弹性系数变化时，会产生稳态误差，这可以通过调节弹簧的预紧力来消除。因此，随着弹簧刚度的增加，超调量增加，振荡加剧。

图8 弹簧弹性系数对气缸位移的影响

4) 主阀芯直径的影响

改变主阀芯外径可以改变阀芯的有效面积，其对控制气缸活塞位移的影响如图9所示。从图中可以看出，3条曲线基本重合，因此，主阀芯的直径变化对控制气缸位移影响不大。

图9 主阀芯外径对气缸位移的影响

2 紧急截断阀控制器参数优化

2.1 优化模型建立

由于截断阀为成品，其参数无法改变，因此主要通过优化控制器的参数，使得截断阀开启特性达到最佳状态。根据1.4节分析，主要通过调节主阀芯质量、阻尼、弹簧刚度对控制器进行参数优化。因此，设计变量为M，B，Kv。

考虑到为了减小截断阀内气体波动造成的振动及噪声，采用优化控制气缸位移的方法，使得控制气缸位移的阶跃响应曲线平稳。因此优化目标函数为：

(9)

下面推导约束条件方程，根据式(1)可得：

(10)

联立式(5)与式(7)，可得：

(11)

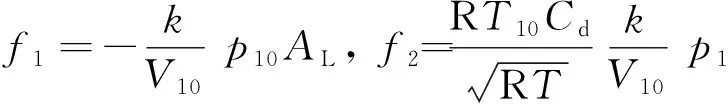
(12)

式中，A1为二位四通阀阀芯开口有效面积，是其阀芯位移x的函数。

A1=kqx+k0

(13)

其中，kq和k0均为系数，kq与二位四通阀阀芯直径有关。

根据式(8)可得：

(14)

考虑到现场实际工况，设计变量的取值范围为：

2≤M≤5 kg； 400≤B≤900 N·s/m； 0.5×105≤Kv≤ 2.5×105N/m。

联立式(10)～式(14)，求解该优化方程，即可得到规定区间内的最优解。

2.2 求解方法

对于微分方程，可以采用龙格-库塔公式求其数值解[15]，不详细叙述。优化过程为：

(1) 变量赋初值，令M=M0，K=K0，B=B0；

(2) 求解方程式(10)～式(14)的数值解，得到y；

(3) 计算式(9)性能指标数值；

(4) 判断ee值是否最小，如果不是最小值，对3个设计变量依次增加一增量，返回式(2)重新求解；

(5) 如果ee是最小值，则优化结束。

2.3 优化结果

根据现场使用工况，二位四通阀入口压力p1=1.0 MPa，截断阀腔体V10=2.5518×10-5m3，T10=293.15 K，控制气缸的BL=730 N·s/m。最终优化结果为控制器的主阀芯质量M=4.7 kg，弹簧刚度kv=85000 N/m，阻尼系数B=840 N·s/m。通过调整主阀芯上的2组YXD唇形密封圈过盈量实现此阻尼系数。唇形密封圈基本内径φ25，外径φ42，宽度8 mm，唇口过盈量1.2 mm。根据优化结果，控制气缸活塞的位移阶跃响应曲线如图10所示。控制气缸内气体压力变化如图11中的“仿真压力曲线”。因为与管道连接的减压阀输出气体压力为1.0 MPa，因此缸内压力最终趋于1.0 MPa。从图10中可以看出，控制气缸活塞位移变化平稳，超调量为0.6%，调节时间为0.03 s，基本没有振荡现象。因此，图11中控制气缸内气体压力变化平稳，只是在上升阶段有小幅波动。

2.4 现场试验

根据优化结果对紧急截断阀控制器进行试验，紧急截断阀快速开启过程中，输气管线内气体压力3.5 MPa，经过减压阀后送入控制气缸的压力为1.0 MPa。试验时测量控制气缸进气压力变化，如图11中的“试验压力曲线”，可以看出控制气缸内部压力基本平稳，与仿真结果比较，超调量有所增加，但误差基本合理。经检测紧急截断阀开启时间小于0.6 s，截断阀开启时的噪声比优化前减小10 dB，因此证明了优化结果的合理性。

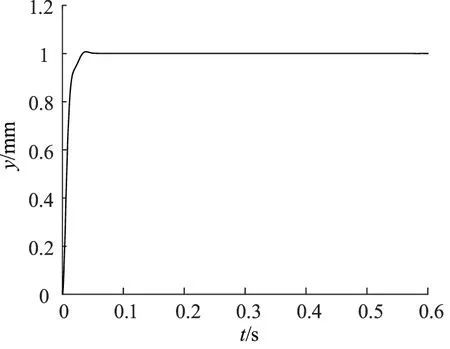
图10 优化后控制气缸活塞位移

图11 优化后控制气缸压力

3 结论

对设计的天然气紧急截断阀控制器进行了瞬态特性分析，并对其参数进行优化，使得紧急截断阀工作更为平稳，主要结论如下：

(1) 建立了紧急截断阀控制器主阀芯、二位四通阀与截断阀控制气缸的数学模型。经分析发现，主阀芯移动存在振荡，导致截断阀控制气缸阶跃响应振荡，控制气缸内气体压力波动，使得截断阀开启瞬间不平稳，截断阀产生振动和噪声；

(2) 分析了控制器主阀芯参数对截断阀控制气缸活塞位移阶跃响应的影响。主阀芯阻尼增加，控制气缸活塞阶跃响应超调量减小，振荡过程减缓，但其峰值时间不变；主阀芯质量增加，超调量下降，响应时间变慢。弹簧刚度增加，超调量增加，振荡加剧；主阀芯直径对控制气缸位移影响不大；

(3) 建立了紧急截断阀控制器参数优化模型。通过优化，截断阀控制气缸活塞位移阶跃响应超调量减小到0.6%，调节时间为0.03 s，基本没有振荡现象，控制气缸内气体压力变化平稳。最后通过试验得到验证。