考虑耐张串效应的特高压线路导线弧垂的理论解

2020-12-04赵腾飞杨垂玮黄模佳

科学技术与工程 2020年30期

赵腾飞，包华，张雷，杨垂玮，周贺，黄模佳*

(1.南昌大学工程力学系，南昌 330031；2.中国能源建设集团安徽省电力设计院有限公司，合肥 230601)

特高压(ultra high voltage,UHV)输电线路中的导线多属于悬索结构，具有高柔性、大位移及非线性的特点[1-3]。导线弧垂是高压架空输电线路设计施工阶段的重要参数之一，导线弧垂的大小直接影响到输电线路的安全稳定运行，因此架空电线弧垂的设计是整个架空电线设计的一个重要环节[4-6]。在以往高压架空输电线路设计中，文献[7]通过悬链线法计算架空线的导线弧垂，但是仅针对未联有耐张串的架空输电线。对于联有耐张绝缘子串的导线弧垂计算设计人员通常采用简支梁法，该方法存在假定，如将耐张绝缘子串假定为直棒形状，耐张串的长度近似为在两悬挂点连线(斜档距)上的投影长度，以及耐张串和导线单位长度自重沿导线两端连线均匀分布，在耐张绝缘子串串长和串重较大的特高压线路中，这对导线弧垂的计算势必会产生误差[8-9]。文献[10-11]采用有限单元方法对悬链线的线性及内力进行分析研究；文献[12]研究了具有刚性端部的悬链线，并给出悬链线的形状；文献[13-16]研究了悬链线悬索的受力及成形的形式；文献[17-19]对悬链线的成形方法进行研究，给出相应的计算方法。目前，对悬链线成形及受力的研究[12-21]仅考虑了悬链线为均匀密度分布，未考虑悬链线两端存在不同密度悬链线的情况(两端存在耐张串)。

根据耐张塔位置的不同，线路档可分为孤立档和连续档两种。孤立档是指中间没有直线塔两端均为耐张塔的档距，而连续档则是在耐张塔中间存在着直线塔的档距，两耐张塔间全部档距构成一个耐张段，在考虑耐绝缘子串计算导线弧垂时，分为一端联有耐张绝缘子串时导线弧垂计算和两端联有耐张绝缘子串时导线弧垂计算两种情况。虽然考虑耐张串影响计算连续档中耐张串相邻档导线弧垂的相关计算方法已有很多，但鲜有采用悬链线法进行导线弧垂计算的文献，而部分涉及孤立档导线弧垂计算的文献[22]计算过程过于简单，计算结果误差较大。为了提高特高压线路设计中导线弧垂计算的精确性，通过悬链线理论对导线和耐张串进行分析，推导出导线弧垂的理论计算表达式，给出一种特高压线路设计的新思路，具有一定的指导意义。

1 利用平衡条件建立导线和耐张串控制方程

在输电线路上除了导线及耐张绝缘子串自重外，档中一般不存在其他荷载。导线所受均布荷载时一般分为两种形式，当均布荷载沿着导线弦线均匀分布时导线呈抛物线形状；当均布荷载沿着导线的弧长均匀分布时导线呈悬链线形状。理论分析结果表明当导线的垂度越小两种形式的差别也就越小[23-24]，为了准确计算出导线弧垂，采用将导线的形状视为悬链线的方法进行分析。采用简化的力学模型进行分析，做以下假定。

(1)导线为既不能受压也不可受弯的理想柔性材料，耐张串呈悬链线形状，材料性质和导线等同。

(2)导线和耐张串上无集中荷载。

(3)忽略导线和耐张串的横截面面积及其自重在外荷载作用下的微小变化量[25-26]。

(4)导线与耐张绝缘子串连接处切线斜率相等，张力大小一样。

首先推导出悬链线一般方程，悬链线受力示意图如图1所示，悬索线在X和Z方向受力的平衡方程分别为

φ为张力V与X轴的夹角；ρ为悬链线的密度；S为悬链线的弧长；φ0为张力U与X轴的夹角；x为悬链线在X轴的投影长度图1 悬链线受力示意图Fig.1 Schematic diagram of catenary force

(1)

曲线积分公式为

(2)

由式(1)平衡方程可得

(3)

(4)

则导线切线方程为

(5)

式中：U为导线的左端拉力；V为右端拉力；导线左端原点切线的斜率为tanφ0；导线右端切线的斜率为tanφ；ρ为导线单位长度的质量；S为导线在x长度上的弧长。

式(4)、式(5)对x求导，得

(6)

两边积分得

(7)

式(7)中：C1为任意的某个常数。

(8)

arcsh(tanφ0)=C1

(9)

联合式(7)和式(9)，得

(10)

式(10)积分，得

(11)

式(11)中：C2为任意的某个常数。

考虑到z|x=0=0，得

(12)

将式(12)代入式(11)，得

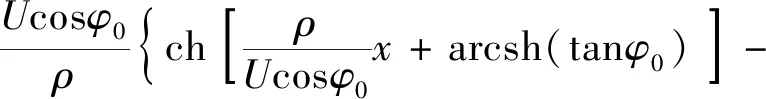
(13)

令

(14)

式(14)中：k为简化计算过程中的替换变量。

则z的积分公式为

(15)

悬链线长度S为

(16)

2 联有耐张串导线弧垂的计算方法研究

当导线联有耐张绝缘子串后，由于耐张绝缘子串单位长度自重比导线单位长度自重大得多，此时耐张串的状态可以等效于悬链线，利用导线和耐张串接点处的一致性，即导线和耐张串接点处的切线相同，张力大小也相同，通过连续性条件求解出联有耐张绝缘子串导线弧垂的精确解。

2.1 一端联有耐张串导线弧垂的计算

连续档耐张段可分为含三挡及其以上的长连续档耐张段和“耐-直-耐”耐张段两种[27]，文献[27-28]验证了耐张串对连续档耐张段中耐张塔相邻档弧垂的影响，说明了计算导线弧垂时考虑耐张串的必要性。为了便于分析，先建立导线一端联有耐张串绝缘子的数学模型，如图2所示，A、E为其中一档导线两悬挂点，AD为导线，DE为耐张绝缘子串，B为档距中点处在导线上一点，C为导线上最低点。

h为悬链线A点到X轴的垂直距离；f为悬链线中点弧垂值；f1为悬链线弧垂最低点到X轴的垂直距离；f2为耐张串D点到X轴的垂直距离；ρ1、S1为悬链线ABCD的密度和弧长，ρ2、S2为耐张串DE的密度和弧长；L1为悬链线弧垂最低点到悬链线A点的水平距离；L2为悬链线弧垂最低点到悬链线B点的水平距离；L为悬链线ABCDE的水平距离，a为耐张串D点到 E点的水平距离；θ为悬链线A、E点连线与X轴的夹角图2 导线一端联有耐张串绝缘子的模型Fig.2 Model of strain string insulator at one end of conductor

取导线最低点C点为坐标原点进行分析，此时φ0=0，由式(15)得

(17)

对导线局部进行分析,如图3所示。

SCD为悬链线CD的弧长图3 导线部分受力示意图Fig.3 Part force schematic diagram of wire

当x=L1时，得

(18)

当x=L2-a时，得

(19)

对隔离体CD导线进行受力分析，其中导线CD长度为

(20)

(21)

则

(22)

再对隔离体DE耐张绝缘子串进行受力分析，此时取D点为坐标原点，如图4所示。

图4 耐张绝缘子串受力示意图Fig.4 Force diagram of anti-tensor insulator string

此时

(23)

式(23)中：k1为简化计算过程中的替换变量。

由式(16)对隔离体DE绝缘子串弧长积分，得

(24)

此时x=a，有

(25)

结合式(18)、式(19)、式(24)及式(25)，求解出未知数f1、f2、L2、a，即得到导线档距中央弧垂f，如式(26)所示:

(26)

式(26)中:zBC为悬链线中B点和C点间的垂直距离，计算表达式为

(27)

2.2 两端联有耐张串导线弧垂计算

孤立档由于两端均为耐张塔，所以档内两端都联有耐张绝缘子串，同样为了便于分析，先建立导线两端联有耐张绝缘子串的数学模型，如图5所示，A、F为两悬挂点，C为档距中心处在导线上一点，D为导线最低点，AB和EF为耐张绝缘子串，BE为导线部分。

f3为悬链线弧垂最低点到X轴的垂直距离；a2为耐张串E、F点的水平距离图5 导线两端联有耐张绝缘子串的模型Fig.5 Model of anti-tensor insulator strings connected at both ends of conductor

首先对其中隔离体BD及DE导线部分进行分析，如图6所示，此时φ0=0，利用式(15)、式(16)得以下公式。

图6 导线部分受力示意图Fig.6 Force diagram of anti-tensor insulator string

当x=L1-a1时，有

(28)

式(28)中：SBD为悬链线BD的弧长。

(29)

当x=L2-a2，有

(30)

式(30)中：SDE为悬链线DE的弧长。

(31)

根据力的平衡方程，有

(32)

(33)

式中：V1、V2分别为悬链线B点、E点的张力，α1、α2分别为悬链线B点、E点的切线与X轴的夹角。

则

对隔离体AB、EF耐张绝缘子串进行受力分析,如图7所示，利用式(14)对隔离体AB和EF绝缘子串弧长积分，得

图7 耐张绝缘子串受力示意图Fig.7 Force diagram of anti-tensor insulator string

(34)

(35)

当x=a1，有

(36)

当x=a2，有

(37)

结合式(29)、式(31)、式(34)～式(37)，求解出未知数f1、f2、f3、L2、a1、a2，即得到导线档距中央弧垂f为

(38)

式(38)中：zCD为悬链线C点和D点间的垂直距离，计算表达式为

(39)

2.3 悬链线法的验证

为了验证悬链线法计算弧垂推导过程和结果的准确性，假设耐张绝缘子串单位长度质量和导线单位长度质量相等，则此时导线一端联有耐张绝缘子串和两端联有耐张绝缘子串计算得到的档距中央弧垂相等，且等于无耐张串时导线档距中央弧垂。

先利用悬链线法推导无耐张串导线弧垂，如图8所示，A、D为两悬挂点，B为导线中点，C为导线最低点。

图8 导线示意图Fig.8 Conductor diagram

由式(17)可得

(40)

(41)

f1=f2+h

(42)

根据式(40)～式(42)平衡方程求解出3个未知量f1、f2、a，则

(43)

式(43)中：zBC为悬链线B点和C点间的垂直距离，计算表达式为

(44)

为了验证公式的正确性，令导线与绝缘子串的密度相同(即ρ1=ρ2)，设高差为10 m，耐张串串长为20 m，导线单位长度重量为40 N/m，验证有无绝缘子串的计算结果是否相同，则导线弧垂计算结果如表1所示。

表1 悬链线法计算导线弧垂验证Table 1 Verification of catenary method for calculating sag of conductor

表1数据表明，当ρ1=ρ2时，有无绝缘子串的计算结果是相同的，证明利用悬链线法计算导线弧垂的公式是正确无误的，可以用于和简支梁法计算导线弧垂进行对比分析。

3 悬链线法和简支梁法差异比较

简支梁法计算一端联有耐张串时档距中央弧垂公式为

(45)

两端联有耐张绝缘子串孤立档的档距中央弧垂计算公式为

(46)

式中：λ为耐张绝缘子串长度，m；L为悬链线的水平距离；ω0为耐张串单位长度所受质量，N/m；ω为导线单位长度所受质量，N/m；F为导线最低点所受水平张力，N；h为档内两端导线悬挂点高，m；θ为线档两端挂点高差角，°。

取特高压直流线路上处于典型气象区为参照，选取导线型号的气象条件为气温15 ℃，耐张串绝缘子串长度为18.26 m，质量为7 291 kg。选取500 m为耐张段的代表档距，高差为15 m。

3.1 气象条件和设计参数

(1)导线型号:导线采用JL1/G2A-1250 /100 钢芯铝绞线，安全系数2.5，单位长度质量4.25 kg/m，平均运行张力占拉断力比值25%。

(2)气象条件:基本风速27 m/s，覆冰15 mm，年平均气温15 ℃，最低气温-15 ℃，最高气温40 ℃。

(3)耐张串:选用串长18.26 m(孤立档时设两端耐张串串长相等)、串重7 291 N的耐张绝缘子串。

3.2 档距中央弧垂计算表达式

架空工况取15 ℃，选取500 m为耐张段的代表档距。采用简支梁法和悬链线法分别计算不同档距下一端和两端联有耐张绝缘子串的档距中央导线弧垂，计算结果如表2、表3所示。

表2 不同档距下的连续档耐张段内耐张塔相邻档弧垂对比Table 2 Comparison of the conductor sag of tension tower in continuous stage tension section of different spans

表3 不同档距下的孤立档竣工弧垂对比Table 3 Comparison of isolated span conductor sag in different spans

从表2、表3可以看出，不论是连续档耐张段内耐张塔相邻档还是孤立档利用2.1节和2.2节中悬链线法计算导线弧垂和简支梁法计算导线弧垂所得的弧垂值基本一致，差值较小。对于连续档耐张段内耐张塔相邻档，当超过一定档距后，其中弧垂差值随着档距的增大随之增大，且高差越大，弧垂差值也越大；而对于孤立档，当超过一定档距后，其中弧垂差值随着档距的增大也随之增大，而高差对弧垂差值几乎无影响。