新型冠状病毒肺炎发病率空间特征及影响因素

周千千，涂 平

(福州大学 数字中国研究院(福建)，福建 福州 350002)

2019年12月31日, 中国湖北省卫生委员会宣布了一系列不明原因的病毒性肺炎病例, 最早的一例发病于2019年12月1日[1]。新型冠状病毒肺炎(2019 novel coronavirus pneumonia，COVID-19)(以下简称“新冠肺炎”)疫情在武汉爆发后，在极短时间内迅速蔓延。截至2020年2月16日，中国报告了新冠肺炎确诊病例58 010例，死亡病例1 772例。新冠肺炎疫情给人类社会造成了巨大的损失与威胁。

目前，不同研究领域的学者已对新冠肺炎疫情进行了大量的研究工作，关注的方向有所不同。基础医疗研究者主要集中在病原学、致病机理、传染源及传播途径等方面的研究[2-3]，其他学科的研究者则大多致力于新冠肺炎的空间扩散特征、发展预测与疾病传播因素的分析[4-9]。在地理学对传染性疾病的研究中,杨斯棋等[10]结合空间分析方法与地理加权回归模型，探究了北京市甲型H1N1流感对气象因子的时空响应规律;李浩等[11]运用时间序列及空间分析方法，分析了宁夏泾源县儿童呼吸系统疾病的区域时空分布规律及区域地理环境因素;陶海燕等[12]运用扩展Knox检验的疾病时空传播网络模型,研究了登革热疫情早期时空传播特征;张利娜等[13]运用因子分析和多元线性回归，分析了健康老年前期女性红细胞比积正常参考值与地理因素的依赖关系，并依此进行了区域划分。

综上，本文按照新增确诊病例数变化趋势划分时间阶段，对新冠肺炎发病率的时空特征及发病率热点区域进行分析，并对新冠肺炎的发病率产生作用的影响因素进行筛选。以新冠肺炎发病率为因变量，以筛选后的空间距离、铁路路网密度、运客率、单位人均床位数4类影响因素为自变量，利用地理加权回归模型对影响因素进行定量分析，利用t值检验确定影响因素的显著性分析了来自地理、医疗、交通等方面的影响因素对发病率的影响，以期为探究新冠肺炎发病率的影响因素提供相关参考。

1 数据与方法

1.1 影响因素指标构建

新冠肺炎发病率的影响因素选择遵循指标可定量表达性和数据可获得性原则。通过参考相关文献[10-11]并结合社会经济数据，从地理空间、医疗设施、交通通达度等多重维度选取影响因素指标。具体影响因素选取如下：(1)疫情的传播以武汉市为中心。从空间上考虑，选取各个城市距武汉市的空间距离探究发病率是否与其密切相关。(2)各类公共交通工具的运转与疫情阻断的矛盾较为突出，而从交通条件考虑疫情传播可分为两类，分别是与其他城市的往来及城市内自身的交通流通水平。选取铁路路网密度衡量与其他城市来往水平，选取单位公共汽车数量、单位出租车数量及运客率3种影响因素衡量城市内部的流通性。(3)医院作为疫情防控的重要单位，医院床位作为诊疗救治的必要条件。选取单位医院数量、单位人均床位数及医生率作为衡量城市医疗水平的指标。最终构建出候选影响因素，如表1所示。

表1 候选影响因素

对表1中各维度下的影响因素进行Pearson相关分析，筛选出与新型冠状病毒发病率呈显著相关的指标。其中，单位公共汽车数量、单位出租车数量、医生率与发病率并无显著相关，故将此3种因素剔除。同时，运用多重共线性检验分析每种影响因素的方差膨胀因子(variance inflation factor, VIF)，以VIF值<7.5为标准确定最终影响因素指标体系。在多重共线性检验中，单位医院数量的VIF值高达8.135，存在变量冗余问题，故将此因素剔除。最终确定的影响因素指标体系，如表2所示。

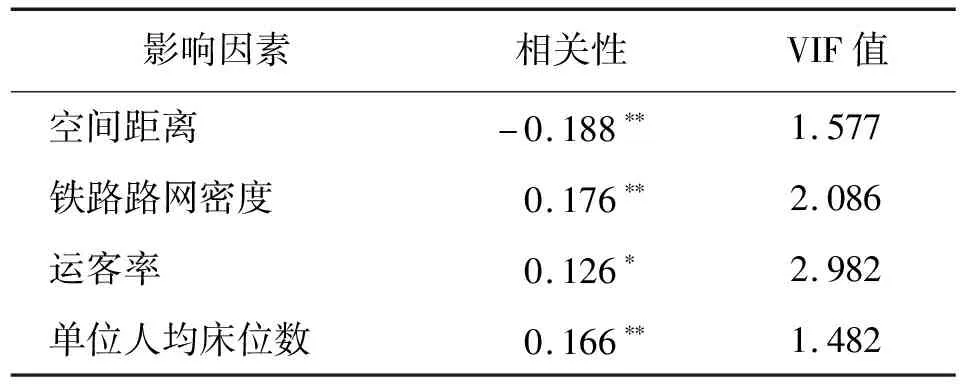
表2 影响因素指标体系

1.2 数据来源与预处理

本文所用的新冠肺炎数据来源于国家卫健委官网发布的每日疫情通报。通过爬虫程序采集了2020年1月26日至2月15日的每日疫情数据，每日采集时间为当日0点。为减少研究分析中的代表性误差，在影响因素显著性分析和空间异质性分析时，本文仅选取采集期间新冠肺炎累计确证病例数大于500的湖北、广东、河南、浙江等10个省市的地级市作为研究对象，样本数量为131。

空间距离由每个城市经纬度与武汉市经纬度计算所得，经纬度数据来自百度地图开发平台；铁路路网数据下载于Open Street Map 开放平台，通过ArcGIS 软件计算每个城市的铁路总长度并除以城市面积以求得铁路路网密度；公共汽车数量、出租车数量、运客量、医生数量、互联网用户数量、城市总人口等社会统计数据均来源于《中国城市统计年鉴》。为消除影响因素量纲带来的数量级差异，采用标准差标准化对各项影响因素进行标准化处理，公式如下：

(1)

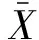
1.3 研究方法

1.3.1空间自相关

空间自相关分析就是研究空间单元观测值是否与其相邻单元的观测值存在相关性的一种分析方法，是空间单元观测值聚集程度的一种度量[14-16]。本文采用全局Moran’sI统计量对发病率分布的空间关联性与差异性进行分析，其计算公式为

(2)

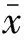
1.3.2地理加权回归模型

地理加权回归(geographically weighted regression，GWR)模型是一种针对空间非稳态数据的局域空间分析方法，能够有效避免自变量系数的均质化，探究研究区域内部的空间变化[17-18]。GWR模型的表达式为

(3)

式中：yi、xik、θi分别为第i个城市的因变量、自变量和随机误差；(ui,vi)为第i个城市的空间坐标；β0(ui,vi)为常数项；βk(ui,vi)为第i个城市的第k个自变量的回归系数。本文以采集期间累计确诊病例数大于500的131个地级市为研究单元，以发病率为因变量，以标准化后的各项影响因素为自变量，根据回归系数在不同空间位置的数值及变化来探究各项影响因素对新冠肺炎发病率的影响程度及空间异质性。

1.3.3影响因素显著性检验

为分析影响因素的边际作用方向差异与各阶段影响因素的时效性，结合GWR结果中各影响因素的回归系数值，将影响因素对发病率的显著性检验值定义如下[10]：

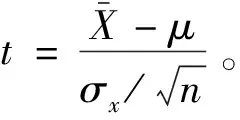
(4)

2 新冠肺炎发病率演变

2.1 新冠肺炎发病率的时间演变特征

2020年1月26日至2月15日新冠肺炎新增确诊病例数时序变化，如图1所示。按照图1时序变化呈现的特征，新冠肺炎新增确诊病例的时序变化分为以下3个阶段：(1)阶段A，1月26日至2月4日，为疫情爆发初期，新增确诊病例数逐渐递增且变化较为平缓，至2月4日新增确诊病例数达到第一个高峰(3 887)是全国确诊病例走势的关键节点；(2)阶段B，2月5日至2月10日，新增确诊病例数由2月4日达到阶段峰值后呈逐步下降的态势，新增确诊病例数有所减少；(3)阶段C，2月11日至2月15日，新增确诊病例数由2月11日起急剧上升，数量突破10 000人达到峰值，继而于2月12日起又呈急剧下降的趋势，并于2月14日起逐渐下降。

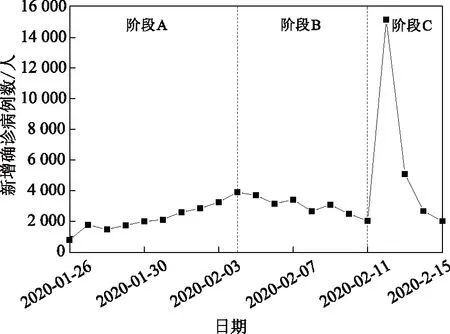
图1 新冠肺炎新增确诊病例时序图

2.2 新冠肺炎发病率的空间演变特征

结合新冠肺炎发病率的时序变化特征，选取上述过程中的3个阶段对新冠肺炎发病率的空间集聚特征进行定量分析。

利用空间自相关方法计算新冠肺炎各个阶段发病率的全局Moran’sI指数，从而确定发病率的空间自相关性及其变化情况，结果如表3所示。由表3可知：各阶段的z值均大于1.96，表明计算结果具有统计学意义，且Moran’sI指数值大于0说明发病率的空间分布具有空间正自相关性，即发病率的值随着测定距离的缩小而变得更相似，由此也说明发病率受到了来自空间距离的影响。其中，A、B、C3个阶段的Moran’sI指数值依次逐渐减弱，直至C阶段Moran’sI指数值达到最小，未达到0.01，从而呈现出较弱的集聚性。发病率在前期新增病例数迅速上升的阶段 A 的空间自相关性强于其余阶段，但整体上均呈现空间集聚特征，且集聚性随时间的推移而减弱。

表3 新冠肺炎发病率Moran’s I指数分析

3 基于GWR模型的影响因素分析

3.1 GWR模型拟合效果分析

分别以A、B、C 3个阶段的发病率为因变量，以表2中的空间距离、铁路路网密度、运客量、单位人均床位数4类影响因素为自变量构建GWR模型，共统计了255个地级城市，样本数量为255，拟合结果如表4所示。由表4可知：阶段A的拟合R2可达0.208，对于发病率空间分异解释度可达20.8%；而在阶段C，GWR模型对于发病率的解释度仅有6.3%，赤池信息量准则(Akaike information criterion，AIC)由533.160上升至882.428。根据已有研究对GWR模型拟合效果的评价标准[19]，AICc值越小则模型拟合效果越佳，而表4中的AICc值由阶段A的533.160上升至阶段C的882.428，则表明GWR模型的拟合效果随时间的推移而减弱。

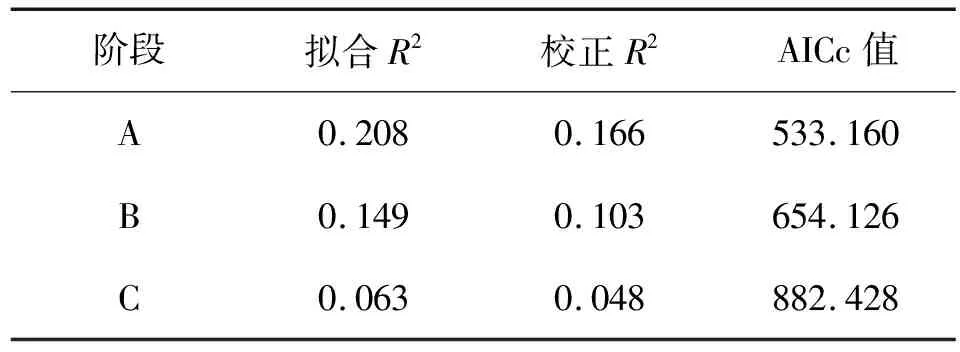
表4 GWR模型拟合结果

3.2 影响因素显著性分析

为探究各类影响因素对新冠肺炎发病率的显著程度，由式(4)计算t值离差统计量，并以累计确诊病例数大于500的10个省市131个地级市为单元进行统计，结果如图2所示。

从图2可知：空间距离、单位人均床位数在A、B、C3个阶段中的t值绝对值均大于1.96，通过了显著性水平为0.05的检验，对新冠肺炎发病率的影响较为显著；铁路路网密度的t值绝对值则在A、B、C3个阶段中均未通过显著性检验，因此，可认为该影响因素对于新冠肺炎发病率的影响不显著，故在后续研究中将铁路路网密度这一影响因素剔除；而运客率仅在阶段A中通过显著性水平为0.1的检验，对发病率的影响程度不如空间距离和单位人均床位数显著。这一现象可能与新冠肺炎疫情后期各大城市公共交通系统防疫启动应急响应机制有关，通过减少公共交通运输以免造成交叉感染，降低了作为衡量城市交通条件水平的运客率对发病率的影响程度[20]。当显著性水平为0.1时，空间距离的检验通过率为100%，运客率的检验通过率为26.1%，单位人均床位数的检验通过率为95.8%。

图2 影响因素t值绝对值柱状图

3.3 影响因素空间异质性分析

将GWR模型中各影响因素的回归系数按累计确诊病例数大于500的10个省市进行统计，结果见表5。由表5可知：空间距离指标是新增病例数变化的负向主导因素，发病率与湖北省的空间距离呈负相关，与湖北省的空间距离越小则发病率越高。回归系数绝对值体现了空间距离指标的强作用区域主要集聚在南部的广东、湖南、江西等省份，表明这些省份的城市受到空间距离的影响程度较大，而与湖北省距离较远的区域的发病率受到来自空间距离的作用力较小，如山东、浙江、江苏等省份。已有研究可知：武汉市作为疫情中心，各省市的病例数均与武汉流入人口数量呈较强的正相关[21]，而近邻的周边南部城市与武汉市的交通往来相比空间距离较远的其他城市更加频繁，接触武汉流入人口的机会也更大；因此，空间距离的作用力也凸显在包括湖北省在内的中南部及东南部地区。因此，在疫情防控中，从空间距离层面考虑，南部地区的防控工作应予以高度重视，尤其是武汉市周边中小城市的卫生医疗条件有限，更应该加强该类地区的管控力度。

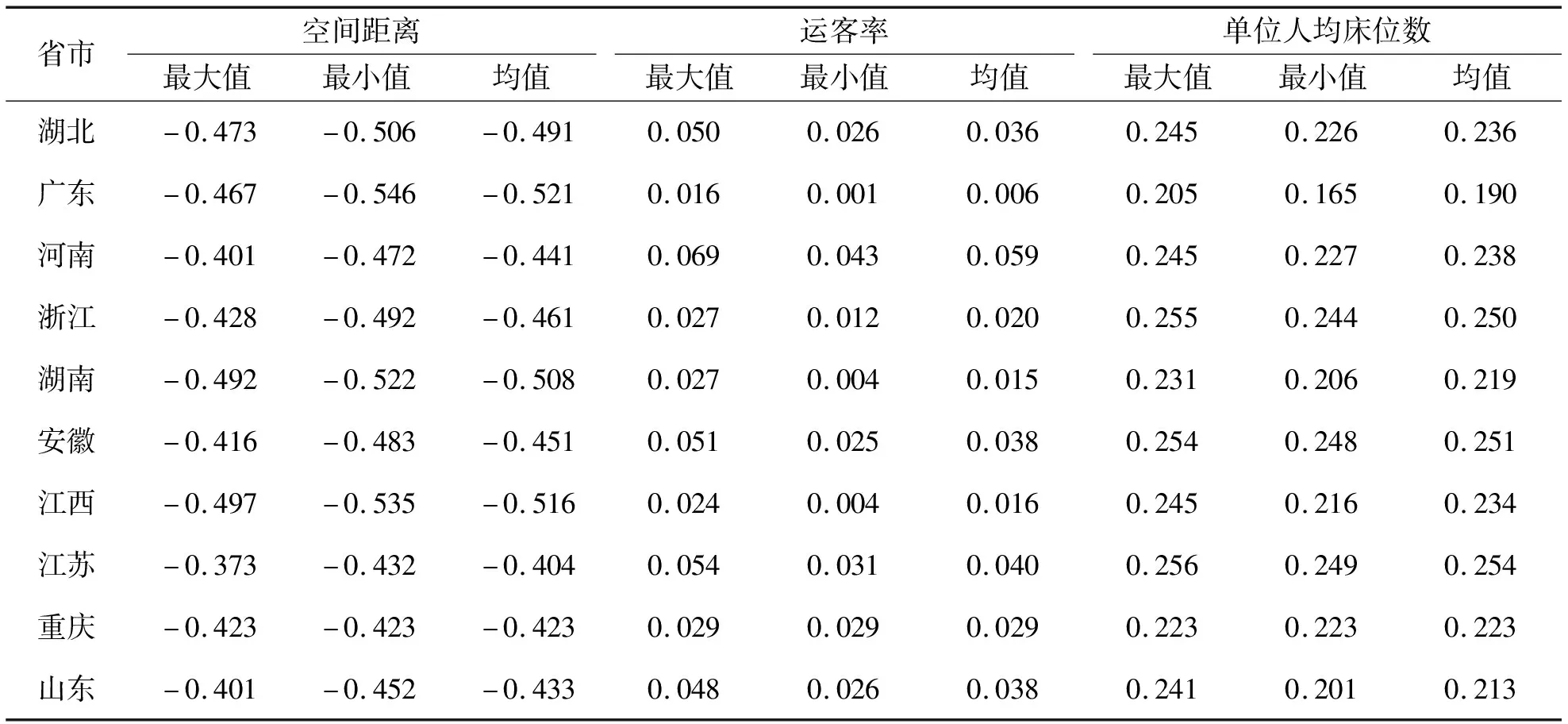
表5 GWR模型回归系数统计

运客率的回归系数均为正，是发病率空间变化的正向主导因素，即一个城市的运客率越高、交通条件越好，则会在一定程度上提高发病率；但该影响因素的整体系数值不高，回归系数值均小于0.1，影响因素作用强度较小。其中，运客率的回归系数高值区域主要集中在河南、江苏、安徽、湖北等省份，应该特别注意此区域的交通流通，适当降低运客率从而降低该地区的发病率。

床位作为诊疗救治的必要条件之一，单位人均床位数却是发病率的正向主导因素，其原因可能与新冠肺炎需要较长的住院时间与治愈周期有关。单位人均床位数的回归系数高值区域主要集中在浙江、安徽、江苏等东部省份。究其原因可知：截至2020年1月23日，武汉市“封城”前迁出人口主要为正常的在外务工或求学返乡人流，但涌出的人数仍是异于往常；而浙江、江苏等东部地区可能会因其优越的医疗条件[22]，从而吸引了部分武汉市迁出人口，导致单位人均床位数的回归系数在该区域内有小幅度提高，回归系数值均大于0.25。

4 结语

新冠肺炎疫情是新中国成立以来在我国发生的传播速度最快、感染范围最广、防控难度最大的一次重大突发公共卫生事件。本文研究能够为疫情的防控工作提供参考：(1)利用地理学的GIS空间分析技术，能够更加精细地获取全国范围内新冠肺炎发病率的时空特征。当前发病率的各方面均处于稳步下降的趋势，各方面的防控工作初见成效，较好地遏制了疫情蔓延势头，但各项防控工作仍然不能放松，以防疫情再次抬头。(2)通过空间距离、铁路路网密度、运客率、单位人均床位数4类影响因素构建GWR模型，探讨了来自地理、医疗、交通等外部因素对发病率的影响程度，并指出了各项影响因素的显著程度及重点作用区域。(3)新冠肺炎发病率在一定程度上还受到了地理空间、交通运转、社会要素等多方面外因的综合作用，但影响发病率的因素复杂多样，后续研究应融合医学、地理学、心理学等多个科学领域，积极运用遥感、交通、社交媒体等多源数据对疫情的防控研究进行深层次分析。

本文存在以下局限性：(1)对于新冠肺炎此类急性传染性疾病，未探讨气象因素，应该在后续研究中补充。(2)相应的防控措施会导致影响因素数值的动态变化，但由于实时数据难以获取，仅以当前可获取的数据衡量了每个城市的医疗、交通的发展水平，若能收集到疫情期间每个城市的新增床位数量与具体铁路交通的变动情况，模型拟合效果将会有所提升。