三八超混沌系统的时滞反馈控制

李德奎

(甘肃中医药大学 理科教学部，甘肃 定西 743000)

美国著名气象学家Lorenz于1963年提出第一个三维连续混沌系统，称之为Lorenz系统[1]，此后，大量的混沌系统相继被提出，比较著名的连续混沌系统有Chen系统[1]、Lü系统[1]和Chua电路系统[2]，离散系统有Logistic映射[3]、Hénon映射[4]等。文献[5]基于Lorenz混沌系统，利用增加状态方程和反馈控制的方法，提出了一个新超混沌系统，由于其混沌吸引子形状出现了数字“3”和“8”的样式，为此将这个超混沌系统称为“三八超混沌系统”。

混沌控制是混沌应用的前提，比较著名的混沌控制方法有：参数微扰法[6]、时滞反馈控制法、自适应控制法、滑模变结构控制法等。时滞反馈控制法是一类重要的混沌控制方法，一方面时滞反馈控制法不需要知道精确的系统模型，这一点是参数微扰法方法无法比拟的；另一方面时滞现象在通信和生态系统中是普遍存在的[7]，例如通信过程中信号传输的拥挤阻塞，捕食者从出生到具有捕食能力，需要一定的成长时间等。因此, 有必要研究时滞反馈控制混沌系统的动力学行为。

许多学者在时滞动力系统方面做了大量工作。文献[8]研究了Arneodo混沌动力系统的时滞反馈控制，分析了系统平衡点的稳定性及局部Hopf分岔的存在性。文献[9]研究了时滞反馈控制Rössler系统的平衡点的局部稳定性和Hopf分岔的存在性。文献[10]研究了一类食饵具有阶段结构的时滞捕食系统的全局稳定性与Hopf分岔。然而这些研究考虑的是三维混沌系统的时滞反馈控制或时滞依赖分析。目前，对时滞反馈控制的四维超混沌系统的动力学研究却较少，同时超混沌系统是比混沌系统更加复杂的动力系统，能够产生更加复杂的时间序列，在保密通信与图像加密领域具有重要的应用价值。

基于以上考虑，本文对三八超混沌系统进行了继续研究，给出了时滞反馈控制的三八超混沌系统模型，分析了其平衡点的稳定性以及平衡点失稳时发生Hopf分岔的参数空间和时滞值。本文的研究可以看成是对文献[8-10]研究成果的进一步推广，具有一定的理论价值。

1 三八超混沌系统

文献[5]基于著名的三维Lorenz混沌系统，利用线性反馈方法，构造了三八超混沌系统，其动力学方程为：

(1)

其中，x,y,z,u为状态变量，a,b,c,θ,k是系统参数。当参数a=10,b=28,c=2,θ=4，k=8时，系统处于超混沌运动状态，具有如图1所示的超混沌吸引子。

图1 三八超混沌系统的混沌吸引子图

2 时滞反馈控制三八超混沌系统

由于时滞是信号传输中不可避免的通信现象，同时也是生态系统平衡性分析必须考虑的问题，因此对三八超混沌系统进行时滞反馈控制，形成如下时滞微分动力系统：

(2)

其中d为时滞反馈系数，τ为时滞常数。易知系统(2)具有唯一的平凡平衡点E=(0,0,0,0)，其平衡点与系统(1)的平衡点相同，说明时滞反馈控制不改变系统的平衡点位置和数量。将系统(2)在平衡点E=(0,0,0,0)处线性化，可得线性系统为：

(3)

根据线性化系统(3)，得其特征方程为，

即，λ4+α3λ3+α2λ2+α1λ+α0+(β3λ3+β2λ2+β1λ+β0)e-λτ=0。

(4)

其中，

当τ=0时，系统(2)由泛函微分方程退化为常微分方程，其平衡点的稳定性在文献[5]中已有研究，并给出有关研究成果如下：

引理1当τ=0时，如果系统(2)的参数满足下列2个条件中的任何一个，

那么系统(2)的唯一平衡点E(0,0,0,0)是渐进稳定的。

本文考虑系统的延迟时滞反馈控制，所以仅考虑时滞常数为正的情况。当τ>0时，设λ=iω(ω>0)是特征方程(4)的一个纯虚根，则由(4)式得ω满足下列关系式，

ω4-α3ω3i-α2ω2+α1ωi+α0+(-β3ω3i-β2ω2+β1ωi+β0)(cosωτ-isinωτ)=0。

(5)

根据复数相等的概念，对(5)的实部和虚部进行分离得方程组(6)，

(6)

方程组(6)可等价转化为，

(7)

对于方程(7)给出下列结论。

定理1如果|α0|<|β0|，那么方程(7)至少有一个正实根。

证明：设v=ω2，则(7)可化为，

(8)

取辅助函数，

(9)

函数(9)可转化为，

(10)

由(4)式、(9)式和(10)式，如果满足，

(11)

假设方程(7)有l(l≤4)个正实根，记为ωn(n=0,1,2,3)，根据方程组(6)可得，

(12)

将ω=ωn代入(12)式，可求得时滞τ的值为，

(13)

证明对特征方程(4)的两边关于时滞τ求微商，可得，

整理为，

λ(β3λ3+β2λ2+β1λ+β0)e-λτ。

(14)

根据(4)式可得，

-(λ4+α3λ3+α2λ2+α1λ+α0)=(β3λ3+β2λ2+β1λ+β0)e-λτ，

(15)

将(15)式代入(14)式可得，

(16)

(17)

(18)

根据欧拉公式e-iω0τ=cosω0τ-isinω0τ可知，|e-iω0τ|=1，所以由(18)式可得，

(19)

化简(19)式可得，

(20)

由(17)式和(20)式可得

(21)

根据以上推导和时滞系统发生Hopf分岔的条件，给出如下结论。

定理4如果条件(H1),(H2)成立，那么当τ∈[0,τ0)时，系统(2)的平衡点E(0,0,0,0)是渐近稳定的。如果条件(H1),(H2),(H3)成立，那么当τ∈τk(k=0,1,2,3…)时，系统(2)在平衡点E(0,0,0,0)附近发生Hopf分岔。

3 数值仿真

为了研究系统(2)在平衡点的稳定性问题，检验定理4的三个条件。数值仿真在满足条件(H1)中①的情况下进行，对于条件(H1)中②的情况与①的情况类似，这里不再赘述。

推论对于如下时滞微分系统，

(22)

(1)当τ∈[0,0.231 8)时，系统(22)的平衡点E(0,0，0，0)是渐近稳定的；

(2)当τ=0.231 8+0.5nπ时，系统(22)的平衡点E(0,0，0，0)附近发生Hopf分岔，出现周期解。

任取系统的初值条件为[x(0),y(0),z(0),u(0)]=[2.5,0,0,0]，在不同的时滞常数下，对系统(22)的稳定性进行数值仿真，仿真结果如图2和图3所示。由图2可以看出，系统(22)在平衡点E(0,0，0，0)附近发生Hopf分岔，出现了极限环。由图3可以看出，系统(22)的平衡点E(0,0，0，0)是稳定的，数值仿真的结果与理论分析的结果一致。

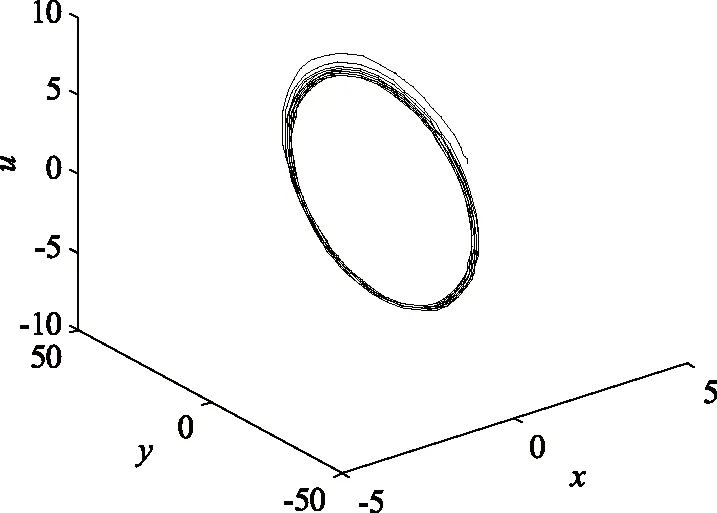
图2 时滞τ=0.231 8时系统(22)的相图

图3 时滞τ=0.013 0时系统(22)的相图

4 结论

本文对三八超混沌系统进行了时滞反馈控制，被控的超混沌系统是一个泛函微分动力系统，通过线性化系统的特征方程根的分布，分析了时滞值对系统平衡点的影响，给出了系统在平衡点附近发生Hopf分岔的参数和时滞条件。本文的研究成果可以看作是对被控三维混沌系统研究的进一步延伸，具有重要的理论意义和应用价值。