基于GLBP约束的非局部均值滤波指静脉图像去噪

2020-12-03蒋寒琼何必锋

杭州电子科技大学学报(自然科学版) 2020年6期

蒋寒琼，沈雷，何晶，何必锋

(杭州电子科技大学通信工程学院，浙江杭州 310018)

0 引言

指静脉技术作为第二代生物识别技术，凭借其良好的保密性、可靠性和便捷性，成为生物识别技术中颇受关注的识别方式之一。实际采集到的图像中往往存在细小颗粒噪声，对指静脉特征提取造成一定干扰，影响指静脉识别系统的性能。目前，常见的图像去噪算法有均值滤波、中值滤波、高斯滤波和非局部均值滤波算法等。均值滤波、中值滤波、高斯滤波只利用图像的局部邻域信息，导致去噪处理后图像模糊。非局部均值滤波(Non-local Means，NLM)算法[1]是空域滤波的一大突破，但是，传统NLM存在图像易平滑过度、权值分配不合理等问题，学者们在传统NLM的基础上进行了改进。文献[2]针对NLM中指数型核函数在权值分配上的不足，提出了一种更符合理想核函数要求的新核函数，改善了权值的分配；文献[3]提出一种结合新余弦函数与高斯函数的新核函数，同时引入邻域相似函数，使得算法中权值的分配问题得到明显改善。但是，上述方法仅利用图像的灰度和距离信息，而颗粒指静脉图像的灰度信息受噪声影响很大，导致邻域块相似度判断不够准确。为此，文献[4]对相似度函数进行改进，虽然结合了梯度信息，但是本质上采用的依旧是图像的灰度信息。文献[5]提出一种动态识别算法来减小噪声对图像的影响，但该方法采用的也是灰度信息。文献[6]采用结构稀疏和高斯尺度混合的编码方式对图像进行重构去噪，但该方法主要适用于边缘纹理信息较强的图像，针对纹理边缘相对模糊的指静脉图像进行去噪时，容易导致细节信息的丢失。为此，本文提出一种基于Gabor的局部二值模式特征编码(Gabor Local Binary Pattern，GLBP)约束的非局部均值滤波指静脉去噪算法，通过Gabor滤波器得到指静脉图像的8个方向响应值，对响应值进行局部二值模式(Local Binary Pattern，LBP)特征编码，得到GLBP纹理特征，利用该特征对去噪算法的核函数进行有效约束。

1 GLBP纹理特征提取

由于Gabor滤波器对光照具有良好的适应性，降低了采集过程中光照变化对图像质量造成的影响。本文结合指静脉具有方向性的特点，采用8个Gabor滤波器来提取在颗粒噪声影响下指静脉图像的8个方向响应值。但是，噪声对Gabor特征的提取造成一定的影响，而LBP具有抗干扰性强、灰度不变性和旋转不变性等优点，因此，本文在Gabor滤波器提取的8个方向响应值的基础上，利用LBP进行特征编码，得到更稳定的纹理特征结构GLBP，有利于后续更好地对指静脉图像进行去噪。

1.1 Gabor方向特征提取

Gabor变换[7]是一种特殊的傅里叶变换，二维的Gabor滤波器是1个由正弦平面波调制的高斯核函数，其数学表达式为：

(1)

x1=xcosθ+ysinθ，y1=-xsinθ+ycosθ

(2)

(3)

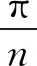
1.2 基于8个方向Gabor响应值的LBP纹理特征提取

图1 8方向响应值分布

LBP算法[8]是一种局部特征描述方法，对颗粒噪声抗干扰能力较强。为了充分利用指静脉图像的8个方向Gabor响应值，采用LBP对8个方向响应值与平均值依次比较，得到1串二进制序列，再转化为十进制，得到GLBP特征值，目标像素点的8个Gabor方向响应值的分布如图1所示。

以图1为例，首先，以P0为起始点，将Gabor的8个方向响应值进行顺时针的方式排列，即P0P1…P6P7。然后，计算Gabor的8个方向响应值的平均值PAVG，按照排序顺序，从P0开始依次与平均值PAVG进行比较，比较结果如下：

(4)

式中，c∈[0,7]。最后，将得到的二进制串转化为十进制，作为该点的GLBP编码数值：

(5)

任意选取手指静脉图像库中一张图像为例，获取该图像某个目标点的8个方向Gabor响应值，并将其量化，再进行LBP编码得到该点的GLBP特征值，具体的提取过程如图2所示。

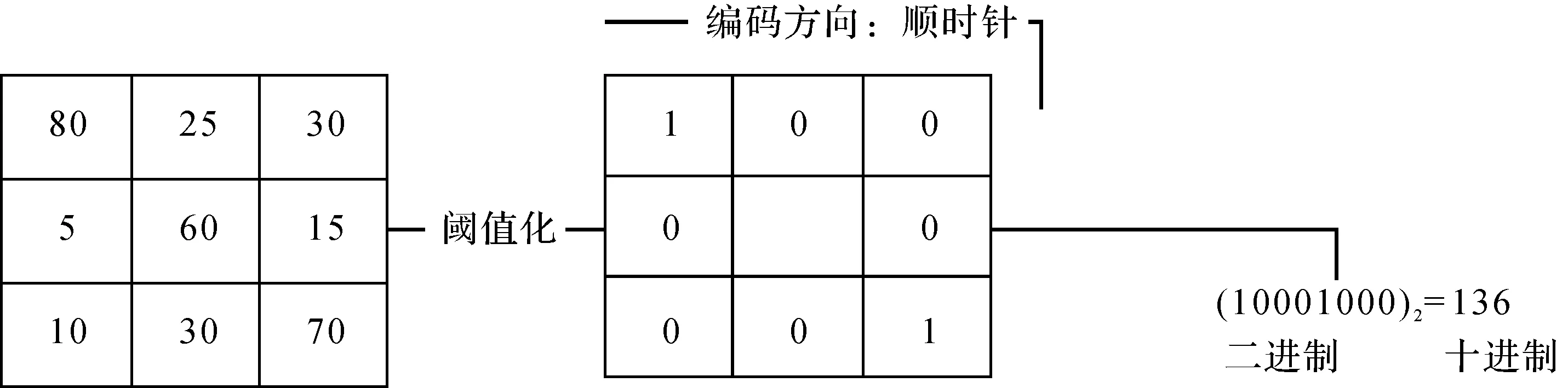
图2 GLBP纹理提取过程

采用图2方法分别对指静脉原图和σ=5加噪处理后的噪声图进行GLBP特征提取，结果如图3所示。对比图3(a)和(b)可以发现，提取的GLBP特征纹理结构与原图静脉结构基本一致，对比图3(b)和(d)可以发现，加噪之后，提取的GLBP纹理特征总体结构与加噪前没有明显差异，说明本文算法提取的GLBP纹理特征具有良好的稳定性和抗干扰性。

图3 加噪前后原图和GLBP特征对比

2 基于GLBP纹理特征约束的非局部均值滤波算法

在NLM算法中，核函数的设置是否合理对图像降噪效果起着至关重要的作用。由于颗粒噪声的存在，指静脉图像的灰度信息受到一定程度的影响，只利用灰度信息相似度进行权值分配，无法很好地进行去噪。GLBP纹理特征在噪声影响下能够保持稳定的纹理结构，具有良好的抗干扰性。当灰度信息出现偏差时，利用GLBP纹理特征计算邻域块之间的纹理相似度，得到基于Gabor的LBP纹理特征相似度(Gabor Local Binary Pattern Texture Feature Similarity，GLBPTFS)，GLBPTFS可以对去噪核函数进行有效约束，使得权重的分配更加合理，保留更多的细节信息，从而提升图像的识别性能。

本文算法实现颗粒噪声图像去噪的主要流程如下。

(1)设定1个以目标像素i为中心的搜索窗口，再设定1个以目标像素j为中心的邻域窗口。

(2)在搜索窗口中移动以j为中心的邻域窗口，利用Gabor滤波器得到在颗粒噪声影响下指静脉图像的8个方向响应值，再利用LBP对8个方向响应值进行编码得到稳定且抗干扰性强的GLBP纹理特征，基于该特征计算邻域块之间的纹理相似度，对去噪核函数进行约束，得到最终的核函数。相似度越高，分配到的权值越大。

(3)根据分配到的权值进行加权得到目标像素i去噪后的像素值。

(4)按照上述步骤对整幅图像的像素点进行遍历，实现对在颗粒噪声影响下指静脉图像的去噪。

本文提出的基于GLBP约束的非局部均值滤波指静脉图像去噪算法核心公式为：

(6)

式中，Ni和Nj分别表示以i为中心的图像块和以j为中心的邻域块，TGLBP(Ni)和TGLBP(Nj)分别表示Ni和Nj所对应的GLBP纹理特征向量，DGLBPTFS(i,j)表示2个邻域块之间的纹理特征差值的绝对值平均，其中DGLBPTFS(i,j)∈[0,255]。

虽然颗粒噪声对指静脉的灰度信息造成一定程度的影响，但是，仍然包含一部分有用信息，因此本文结合灰度和距离信息对邻域块之间的相似度进行计算，得到高斯加权欧氏距离d(i,j)。在邻域纹理相似度的基础上，用d(i,j)进行修正，其核函数公式如下：

(7)

经过大量的实验得到，当α1=0.52，α2=0.48时效果最佳，其中α1+α2=1，cos2(·)为新余弦函数，利用新余弦函数使得权值的分配更加符合理想核函数的要求。h,h1,N为平滑参数，h由噪声标准差σ决定，h1取为DGLBPTFS(i,j)的理论最大可能值255，N取为2。

(8)

最后，将式(7)代入式(8)，得到最终的权值w(i,j)，根据最终的权值进行信息加权得到目标点i的像素值，实现图像的去噪。其中，Z(i)为归一化函数。

3 实验仿真结果

实验采用的是由自主研发的850 nm波长红外摄像头的小型指静脉模块采集的200类正常图像库，每类手指有20幅图，共4 000幅图像；100类粉尘图像库，每类10张，共1 000幅图像。采用的图像尺寸为500×200，仿真软件采用的是MATLAB2014a软件编程，电脑采用的是Windows7 64位操作系统，Intel(R) Core(TM)i3-4170主频3.70 GHz，内存为4 GB。

3.1 PSNR对比图

对200类正常图像库进行不同程度的加噪处理后得到加噪图像库，对加噪图像库和粉尘图像库分别进行去噪处理。传统NLM算法的滤波系数h=σ，能够根据噪声标准差的大小自适应调整滤波参数，因此，本文利用该模型来确定加噪图像库的滤波参数。经过研究发现，粉尘图像库的噪声程度与σ=10加噪处理下的图像比较接近，因此粉尘图像库采用的平滑系数h=10。实验采用5×5的相似窗以及11×11的搜索窗。分别采用本文算法、传统NLM算法[1]、非线性核函数的NLM算法[2]、引入邻域相似函数的NLM算法[3]和Sparse Coding算法[6]对噪声图像库进行去噪处理，不同算法去噪处理后取平均得到的峰值信噪比(Peak Signal to Noise Ratio，PSNR)比对结果如表1所示。

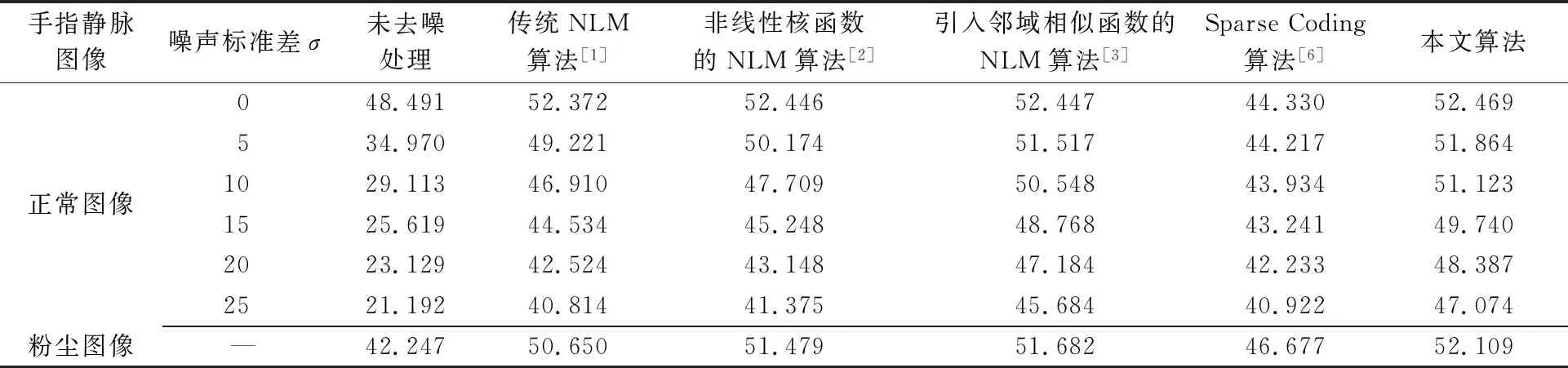
表1 不同算法对加噪图像去噪后峰值信噪比比较 dB

由表1可以看出，相较于传统NLM算法，经过本文算法去噪后的图像PSNR值平均提升了3.677 dB，而且对于不同程度的颗粒噪声，本文算法的PSNR始终高于其他几种算法，且由于在不同加噪情况下，GLBP特征依旧具有良好的表征图像静脉信息的能力，对去噪核函数能够进行较好的约束，因此随着σ的增大，本文算法优势更加明显。

3.2 ROC曲线对比图

选取在σ=15加噪下的噪声图像库和粉尘图像库，利用本文算法、传统NLM算法[1]、非线性核函数的NLM算法[2]、引入邻域相似函数的NLM算法[3]和Sparse Coding算法[6]分别进行去噪，并对去噪后的图像经过Niblack二值化分割[9]、查表法细化[10]得到静脉骨架特征，然后采用修正的Hausdorff距离识别算法(Modified Hausdorff Distance，MHD)来识别性能分析[11]，使得加噪图像库内图像互相匹配，得到加噪图像库类内匹配数据38 000个和类间匹配数据7 960 000个，总计7 998 000个匹配数据，粉尘图像库类内匹配数据4 500个和类间匹配数据495 000个，总计499 500个匹配数据，不同去噪算法的ROC(Receiver Operating Characteristic)曲线如图4所示。

由图4可知，本文算法的ROC曲线最贴近坐标轴，说明本文算法无论在控制拒真率还是认假率上，性能都优于不作去噪处理以及其余4个去噪算法。结合PSNR结果，可以得到经过本文算法处理之后的图像不仅得到了更好的去噪效果，并且增强了对细节的保护能力。在零误识下，相较于传统NLM算法，拒真率平均下降了9.695%。