高分辨宽测绘带SAR频域NLCS成像算法
2020-12-03陈国瑾章坚武
陈国瑾,刘 静,章坚武,钟 华
(杭州电子科技大学通信工程学院,浙江 杭州 310018)
0 引 言
合成孔径雷达(Synthetic Aperture Radar, SAR)[1]利用雷达平台与目标的相对运动将真实天线孔径合成为大尺寸的等效孔径,具有全天时全天候等多种优势,在军事和民用领域发挥着重要作用。然而,SAR回波信号复杂的二维空变特性和严重的距离单元徙动(Range Cell Migration, RCM)给成像处理带来了巨大的挑战。
非线性变标(Non-Linear Chirp Scaling, NLCS)算法是经典的SAR成像算法,具有优秀的空变处理能力,成像效果良好。2012年,An D.X.等[2]提出改进的NLCS算法,通过方位向引入预滤波处理提高分辨率。2014年,Li D.等[3]提出一种改进的方位NLCS算法,能准确校正RCM并解决多普勒调频率空变问题。2017年,Li D.等[4]对方位NLCS算法进行完善优化,通过对二维空变的距离徙动进行校正,并对方位空变的多普勒参数进行均衡从而实现高分辨率成像。2018年,张松[5]通过构建新的几何模型提高NLCS方位向处理精度,实现SAR高分辨成像。然而这些算法以斜视角固定不变为前提,在处理信号过程中忽略了多普勒中心空变问题,随着斜视角增加和测绘带变宽,多普勒中心空变严重,传统算法难以适用。因此,本文对高分辨宽测绘带SAR的回波特性进行分析,构建以x轴点目标为参考点的模型,在频域改进NLCS的均衡与压缩处理函数,提出一种改进的频域非线性变标(Frequency Non-Linear Chirp Scaling, FNLCS)算法。
1 信号模型及空间斜视角空变分析
SAR的几何构型如图1所示,SAR系统平台的飞行速度为v,在t=0时,坐标为(0,yr,hr),hr为机载平台高度。P0(x0,y0,0)为场景中心点目标,P(x,y,0)是成像区域的任意点目标,θg为地面斜视角,Rg为任意点目标到y轴的地面距离。点目标的收发斜距和Rtot泰勒级数展开式为:
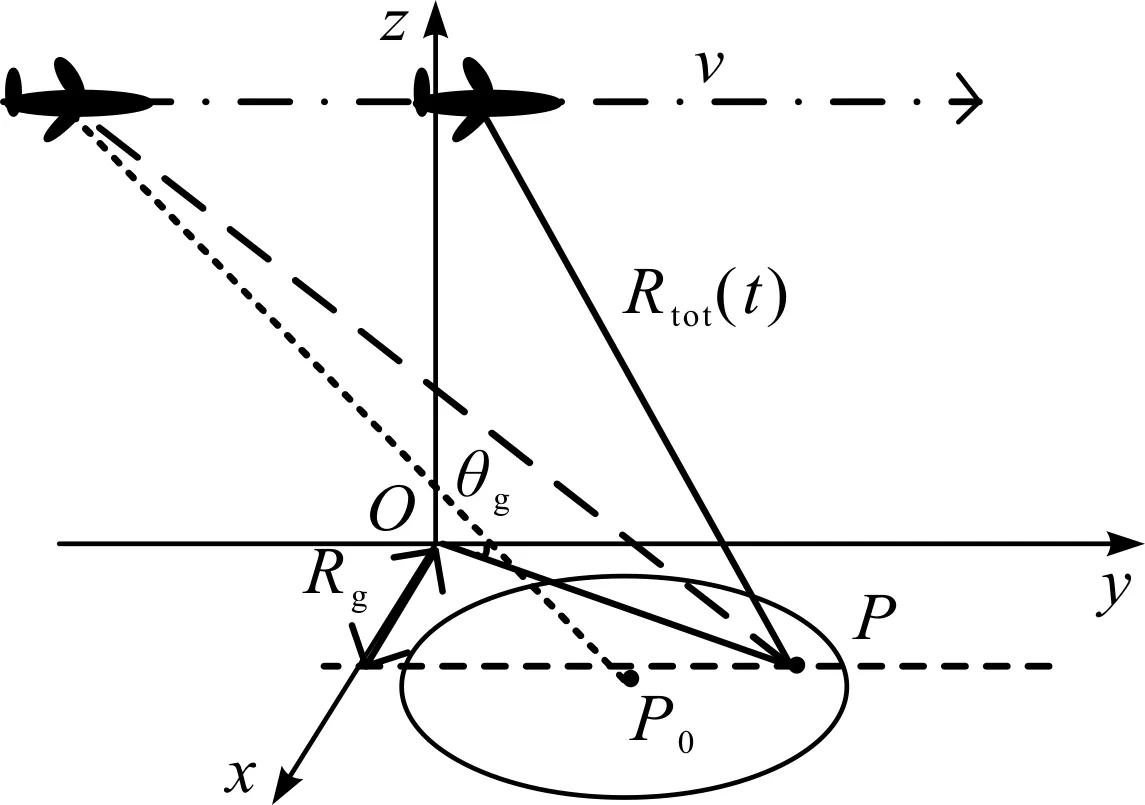
图1 机载斜视SAR的几何构型
(1)
式中,t为方位慢时间,Z0为t=0时刻点目标的收发斜距和,R0为Z0的一半,A0,B0和C0为展开系数。
假设雷达发射线性调频信号,载波频率为fc,则点目标回波信号经过解调之后为:
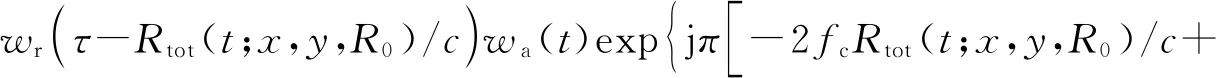
(2)
式中,τ为距离向时间,wr(·)和wa(·)分别为距离向包络和方位向包络,j为虚部,c为光速,Kr为距离调频率。
传统算法以空间斜视角固定不变为前提,但实际探测中,空间斜视角随地面距离变化。根据文献[4],斜视角与地面距离的关系式可表为:
(3)
式中,θ为目标点处的空间斜视角,θ0,α0,R0分别为参考点处的空间斜视角、下视角和波束中心斜距,θg为地面斜视角,ΔRg为目标点到参考点处的地面距离。
由式(3)可知,空间斜视角随着点目标位置变化的,从而使得点目标多普勒中心具有空变特性,传统算法忽略了空变的多普勒中心,导致方位向处理误差严重,成像性能严重下降。因此,本文将针对上述问题进行算法改进。
2 距离向处理
将回波信号(2)转换到距离频域-方位时域:
(4)
式中,信号的包络不影响最终的聚焦结果,故将其忽略,fr为距离向频率。
首先,通过线性距离走动校正(Linear Range Walk Correction, LRWC)去除大部分线性RCM,并减少回波数据的距离方位耦合程度,同时一定程度上校正多普勒中心频率,处理函数为:
(5)
式中,A0ref为场景中心点的零阶泰勒级数展开系数。将式(4)和式(5)相乘得到处理结果为:
(6)
式中,A1=A0-A0ref为残余线性RCM。
然后,通过梯形变换(Keystone Transform, KT)完全去除残留的线性RCM。KT处理的本质是重采样过程,即t=fcta/(fc+fr),将处理结果在fr=0处泰勒级数展开为[6]:
(7)
式中,φ0为方位调制项,φ1为距离位置项,φ2为距离调频项,φ3为高次距离方位耦合项。
最后,以场景中心点为参考点进行一致距离单元徙动矫正(Bulk Range Cell Migration Correction,Bulk RCMC)处理,处理函数为:
(8)
Bulk RCMC能够校正剩余的RCM分量,并消除了距离-方位耦合,距离向处理全部完成。
距离向处理后,点目标的距离历程发生变化,由式(1)中Z0+A0t+B0t2+C0t3搬移到Z0处,并以此为基础进行方位向处理[7]。先将方位调制项φ0重新写为:
(9)
式中,λ为信号波长,fdc(R0)为多普勒中心,Ka(R0)为多普勒调频率,Kt(R0)为高次相位参数,R0为距离向处理后的距离单元。将φ1转换到方位频域可得:
(10)
式中,fa为多普勒频率,fdr(R0)=1/Ka(R0)。
由上述分析可知:距离向处理不能完全去除多普勒中心,同一距离单元的点目标多普勒中心存在空变特性。因此,残余的空变多普勒中心需在方位向处理中去除。
3 参考点分析
距离向处理中距离历程的变化过程如图2所示,任意3个点目标A,B,C在方位零时刻与机载平台的斜距是不同的,在距离向处理后,点目标A,B,C被校正到同一距离单元,但是,由于多普勒参数存在空变特性,无法统一聚焦,因此,需要选取适当的参考点,并推导其他点目标的多普勒参数与参考点参数的空变关系,从而进行FNLCS方位均衡,去除多普勒参数空变分量。
在方位零时刻,除了场景中心点外,其他波束中心照射的点目标坐标未知,因此,传统算法的参考点选取不适用。基于上述考虑,本文将距离单元R0作为一个自由度,选取位于同一距离单元且在x轴上的点目标作为参考点,并推导参考点x轴坐标与距离单元R0的关系式为:
(11)
其次,参考点的x(R0)不同,导致其多普勒中心fdcref存在差异,推导参考点的多普勒中心表达式为[8]:
(12)
4 方位向处理
依据式(12)进行频谱搬移,处理函数为:
(13)
将式(13)与信号相乘后,可以得到信号经过频谱搬移后的相位为:
(14)
接着将信号进行三阶预滤波,为后续FNLCS推导增加足够的自由度,并通过驻定相位原理将信号变换到方位频域为[9]:
(15)
式中,Y为预滤波参数,fn为频谱搬移后的多普勒中心,即fdc(R0)-fdcref(R0)。
为了描述多普勒参数的空变特性,在fn=0处对多普勒参数进行级数展开,可得:
(16)
由式(16)可知,多普勒参数被分为非空变部分和空变部分。非空变部分参数fdr0(R0)和Kt0(R0)容易统一补偿,而空变部分通过在频域引入NLCS因子q3,q4来均衡处理,处理函数为:
(17)
将式(17)与信号相乘后的结果转换到方位时域,整理得到:
(18)
观察式(18)的相位,第1项为常量,对聚焦效果无影响,可以忽略;第2项为方位调频项;第3项为点目标在方位频域的成像位置;第4项为频域偏移。剩余空变的多普勒调频率和高次相位是影响方位聚焦的主要因素,为了消除空变对成像的影响,将其系数设为0,可得:
P3(R0)=0,P4(R0)=0,P5(R0)=0
(19)
通过式(19)的计算结果得到方位压缩系数,可以明显看到多普勒参数的空变被消除,即
(20)
信号完成方位压缩,转换到方位频域即可得到最终的聚焦图像。
5 仿真实验
实验中,机载SAR仿真参数如表1所示,对5个点目标进行仿真模拟,点目标位置如图3所示,距离向间隔和方位向间隔都是1 000 m。本文算法的最终成像结果如图4所示,从图4可以看出,成像场景内点目标的聚焦效果良好。
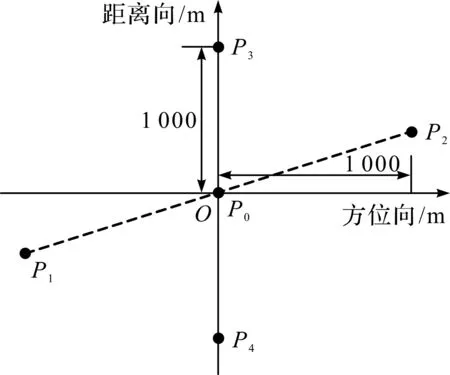
图3 仿真区域点目标位置示意图

图4 本文算法整体成像结果
为了验证本文算法的成像性能,将文献[4]的传统算法和本文的改进算法的聚焦效果进行对比,并对边缘点P1的聚焦图像和聚焦方位向剖面图进行分析。图5为P1点的聚焦图像,相较于传统算法,本文算法聚焦效果良好。图6为方位向剖面图,传统算法的方位向剖面图较差,本文算法很好地解决了多普勒中心空变问题,剖面图旁瓣低于-13 dB并且对称。表2给出了2种算法中边缘点目标P1和P2的聚焦性能指标,可以看到,传统算法得到的性能指标较差,尤其是在方位向上,而本文算法的成像性能指标都接近理论值。
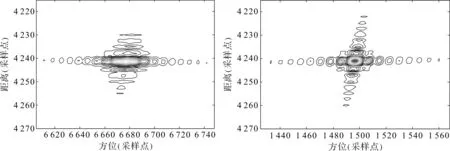
图5 不同算法的聚焦效果
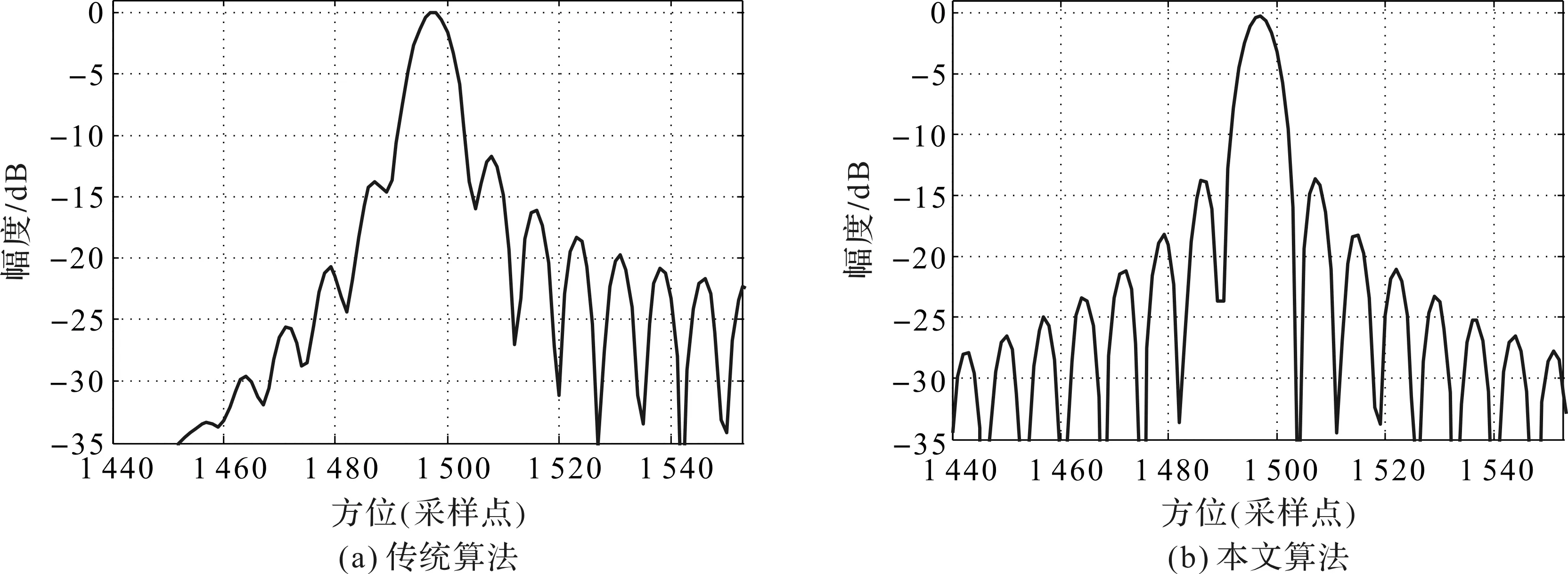
图6 不同算法的聚焦方位向剖面图

表2 不同算法边缘点目标的聚焦性能指标 dB
6 结束语
本文针对SAR成像中面临的多普勒中心空变的问题展开研究,通过构建新的参考点和空变模型,改进FNLCS算法的均衡函数和压缩函数,成像效果良好。本文构建的基于目标坐标的距离模型、空变多普勒参数的分析过程及成像算法为双基SAR、前视SAR等新体制雷达成像方式的研究提供了研究思路。
