协正张量互补问题的例外族和解的存在性

金 珂，凌 晨

(杭州电子科技大学理学院，浙江 杭州 310018)

0 引 言

协正矩阵是半定矩阵的推广，协正张量互补问题是协正矩阵互补问题的推广。文献[1]阐述了协正矩阵互补问题的一些研究成果。文献[2]研究了协正张量互补问题与许多张量优化问题的关系。例如，一类带协正张量约束的张量优化问题的一阶最优性条件可直接表示成张量方程[3]或协正张量互补形式，而后者在数据挖掘、机器学习和大数据分析中均有广泛应用[4]。本文针对协正张量互补问题，研究其解的存在性性质，利用拓扑度[5]理论和例外族[6-7]概念，证明了协正张量互补问题的3个存在性结论。

1 问题描述

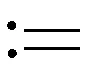
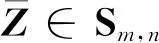
(1)

2 预备知识

设Ω⊂Rn是有界开集，用∂Ω表示Ω的边界，clΩ表示Ω的闭包。设F∶clΩ→Rn是连续函数，b∈Rn。若b∉F(∂Ω)∪F(WF)，则定义F在b处关于Ω的拓扑度为

其中，WF={x∈clΩ|JF(x)=0}，F-1(b)={x∈Rn|F(x)=b}，JF(x)为F在x处的Jacobian行列式，sign(t)是符号函数，即

由于WF为零测度集，利用拓扑度在邻近b处的保值性质，可以进一步对满足b∉F(∂Ω)的b∈Rn定义deg(F,Ω,b)。

定理1(Poincaré-Bohl定理)[5]设Ω是Rn中的有界开集，F,G∶clΩ→Rn是连续函数，b∈Rn。若b∉{H(x,t)|x∈∂Ω,t∈[0,1]}，则

deg(F,Ω,b)=deg(G,Ω,b)

其中H(x,t)=tF(x)+(1-t)G(x)和t∈[0,1]。

定理2(Kronecker定理)[5]设Ω是Rn中的有界开集，F∶clΩ→Rn是连续函数，b∈Rn。若b∉F(∂Ω)且deg(F,Ω,b)≠0，则F(x)=b在Ω中必有一解。

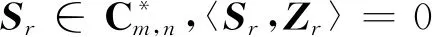
(2)

则称{Zr}为COTCP(1)的例外族。

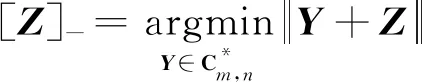
引理1设A,B∈Sm,n。下面2个结论等价。

(2)A=[A-B]+。

证明首先证明由结论1可推出结论2。

任取Q∈Cm,n，均有

然后证明由结论2也可推出结论1。

(3)

由引理1，得出如下引理。

引理2设F∶Sm,n→Sm,n是连续函数。则Z是COTCP(1)的解，当且仅当Z=[Z-F(Z)]+。

引理3设F∶Sm,n→Sm,n是连续函数。则COTCP(1)有解，当且仅当存在Z∈Sm,n，使得[Z]-=F([Z]+)。

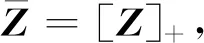
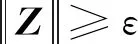
定义3[9]设函数G∶Cm,n→Sm,n。若存在有界闭集D⊂Cm,n，对任意的Z∈Cm,nD，均可找到Y∈D，使得〈G(Z),Z-Y〉≥0，则称G在Cm,n上满足Karamardian-type条件。

则称G在Cm,n上是p阶强制的。当p=1时，称G在Cm,n上是强制的。

3 例外族和解的存在性

首先给出COTCP(1)解的存在性质。

定理3设F∶Sm,n→Sm,n是连续函数，则COTCP(1)要么有解要么有例外族。

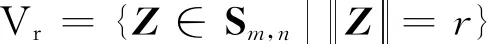
下面分2种情况讨论。

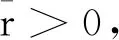
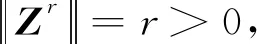
tr[Zr]++(1-tr)F([Zr]+)=[Zr]-

(4)

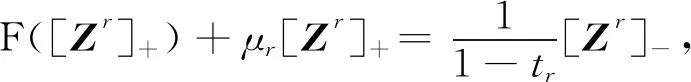
定理4设F∶Sm,n→Sm,n是连续函数。若F满足Isac-Carbone-type条件，则COTCP(1)是有解的。

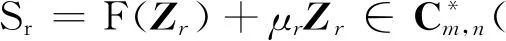
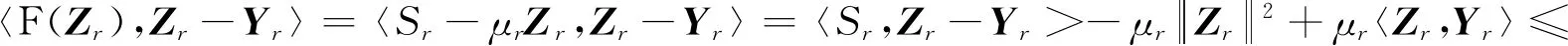
这是一个矛盾。证毕。

定理5设F∶Sm,n→Sm,n。若F在Cm,n上满足Karamardian-type条件，则F在Cm,n上满足Isac-Carbone-type条件。

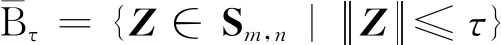
由定理4和定理5知，对于F∶Sm,n→Sm,n，只要F在Cm,n上满足Karamardian-type条件，则COTCP(1)是有解的。

定理6设F∶Sm,n→Sm,n是连续函数。若存在p∈(-∞,+∞)，使得F是p阶强制的，则COTCP(1)必有解。

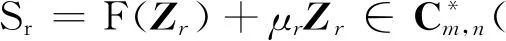
由此知，对于任意充分大的r>0，均有

(5)

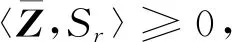
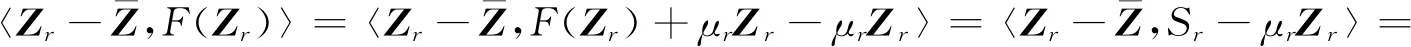
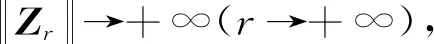
通过一个实例来说明，在张量情形下，函数的p阶强制性条件是合理的。此时，相应的COTCP(1)是有解的。

进一步，由矩阵P的正交性，易知

所以，有

由此知，F(Z)在C2,n上是p阶强制的，其中p∈(-∞，2)。从而由定理6得，COTCP(1)是有解的。

4 结束语

本文研究一类新的协正张量互补问题解的存在性质。首先，借助拓扑度理论和例外族概念得到协正张量互补问题或有解或有例外族，两者必居其一；然后，进一步证明了在Isac-Carbone’s条件、Karamardian’s条件及F的p阶强制性条件下，协正张量互补问题必有解。下一步将针对求解协正张量互补问题的数值算法展开研究。